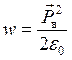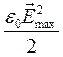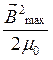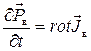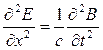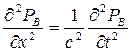научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2012
DOI: 10.7463/0612.0425164
УДК: 537.86; 534.01
Россия, МГТУ им. Н.Э. Баумана
Не множьте сущностей без
крайней на то необходимости.
«Бритва Оккама»
Современная теория электромагнитных волн базируется на фундаменте уравнений Максвелла. Волновые уравнения представляют собой дифференциальные соотношения, в которых участвуют полевые электромагнитные величины напряженность электрического поля Е и индукция магнитного поля В.
В работе показана возможность описания электромагнитных волн в вакууме с использованием физических величин (ФВ) поляризованность Р и намагниченность J, которые в авторской системе физических величин и закономерностей (ФВиЗ) [1, 2] входят в отдельную системную группу, куда также входят электрический заряд, сила тока и другие им подобные (с размерностной точки зрения) величины. Эту системную группу электромагнитных ФВ автор назвал базовыми электромагнитными величинами.
Другая системная группа электромагнитных величин, не входящих в группу полевых и образующих две отдельные подгруппы ФВ, обратных по размерности, названа автором структуро-средовыми величинами. В эту группу ФВ входят емкость, индуктивность, электрическая проводимость, электрическая постоянная, магнитная постоянная и другие величины. Обе эти группы автор называет «материальные» электромагнитные ФВ, чтобы отличать их от полевых величин. Более подходящего названия не нашлось, поскольку виртуальные частицы трудно отнести к полевым или вещественным структурам, а емкость и индуктивность вещественными назвать тоже нельзя, это же не конденсатор или катушка индуктивности. Отнесение же этих параметров к материальным в определенной мере оправдано, поскольку и поля тоже считаются материальными.
Таким образом, под «материальными» электромагнитными ФВ далее будут пониматься зарядо-токовые и структуро-средовые ФВ, образующие в системе ФВиЗ свои отдельные системные уровни, отличные от уровня полевых ФВ.
Поляризованность и намагниченность, входящие в состав зарядо-токовых ФВ, обычно используют в качестве статических электромагнитных характеристик вещественных сред. Однако эти характеристики вполне можно использовать и для описания динамических волновых процессов, происходящих как в вещественных средах, так и в вакууме. Основанием для этого служат современные представления о вакууме как о динамической материальной среде, в которой непрерывно появляются и исчезают виртуальные частицы. Считается, что виртуальные частицы появляются на очень короткое время и исчезают парами. При этом они обладают, как и обычные вещественные частицы, электрическим зарядом, массой, магнитным моментом, механическим моментом и другими характеристиками. Благодаря этому качеству и другим, еще не совсем понятным современной науке свойствам, вакуум способен поляризоваться [3] и быть проводником электромагнитных волн. В динамических электромагнитных процессах вакуум обладает, по мнению автора, наряду с поляризуемостью свойством намагничиваемости, поскольку в динамических процессах эти два свойства неразделимы и всегда сопутствуют друг другу.
Далее будет обосновываться использование ФВ поляризованность и намагниченность вместо полевых величин, в том числе и при описании волновых процессов. Преимуществом такого описания является то, что появляется возможность создания модельного представления об электромагнитных волнах. Создать подобные наглядные физические модели для полевых величин, по мнению автора, не представляется возможным.
Поляризованность и намагниченность сред по определению являются объемными плотностями соответственно - электрического дипольного момента и магнитного дипольного момента. Оба названных параметра модельно представимы, что хорошо известно. Эти модели достаточно наглядны и понятны. Параметры поляризованность и намагниченность, по мнению автора, применимы и к вакууму по причине наличия в нем виртуальных частиц. В математической форме выражения этих параметров следующие:
 , (1)
, (1)
 . (2)
. (2)
В формуле (1) обозначено: ![]() - суммарный электрический момент виртуальных частиц вакуума в объеме
- суммарный электрический момент виртуальных частиц вакуума в объеме ![]() ;
; ![]() - поляризованность (векторная величина), возникающая при волновом возмущении вакуума.
- поляризованность (векторная величина), возникающая при волновом возмущении вакуума.
В формуле (2) обозначено: ![]() - суммарный магнитный момент виртуальных частиц вакуума в объеме
- суммарный магнитный момент виртуальных частиц вакуума в объеме ![]() ;
; ![]() - намагниченность вакуума (векторная величина), возникающая при волновом возмущении вакуума.
- намагниченность вакуума (векторная величина), возникающая при волновом возмущении вакуума.
Объемная плотность энергии (![]() ) электрической и магнитной составляющих электромагнитной волны в вакууме, если её выразить через вещественные параметры (1) и (2), должна определяться следующими соотношениями:
) электрической и магнитной составляющих электромагнитной волны в вакууме, если её выразить через вещественные параметры (1) и (2), должна определяться следующими соотношениями:
 , (3)
, (3)
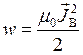 . (4)
. (4)
В этих выражениях: ![]() - электрическая постоянная;
- электрическая постоянная; ![]() - магнитная постоянная. Ранее их именовали электрическая проницаемость и магнитная проницаемость вакуума. Системно эти ФВ входят в группу структуро-средовых величин.
- магнитная постоянная. Ранее их именовали электрическая проницаемость и магнитная проницаемость вакуума. Системно эти ФВ входят в группу структуро-средовых величин.
Для наглядности изложения последующего материала используем отдельные изображения авторской системы ФВиЗ (см. рис. 1 - рис. 5). Преимущество использования данной системы в физических исследованиях - объективное структурирование всей совокупности ФВ, включая электромагнитные, на отдельные системные группы, которые характеризуются общностью размерностного выражения входящих в них ФВ и, соответственно, общностью их свойств. Система ФВиЗ обладает также наглядностью изображения физических закономерностей и формализованным механизмом поиска и обнаружения этих закономерностей.
О принадлежности ФВ к определенным системным группам свидетельствует отличительная окраска, применяемая для удобства пользования системой. Отличительная окраска различных групп ФВ помогает оперативно ориентироваться в системе и правильно выделять системные закономерные связи, иллюстрирующие природные закономерности. Системные закономерные связи обнаруживаются путем построения выделенных параллелограммов (или выделенных линий, представляющих собой параллелограмм, наблюдаемый «в профиль»), в которых соблюдается определенное правило. Это правило заключается в равенстве произведений (отношений) размерности ФВ, оказавшихся на противоположных (смежных) вершинах выделенного параллелограмма.
Приводимые на рисунках цветные пиктограммы призваны облегчать поиск системных закономерностей. В системных закономерностях имеет место не только парное равенство произведений (отношений) размерностей ФВ, располагаемых на противоположных (смежных) вершинах выделенного параллелограмма, но и взаимное уничтожение дополнительных размерностных коэффициентов, присущих каждому системному уровню. Об этих коэффициентах можно узнать из работы автора [1].
На рис. 1 приведены системные соотношения, показывающие происхождение полевых электромагнитных величин - как соотношений «материальных» (зарядо-токовых и структуро-средовых) ФВ.

Рис. 1. Системные закономерные связи полевых и «материальных» электромагнитных величин
Математические выражения, определяющие векторные полевые величины Е и В согласно системным соотношениям рис.1 (для вакуума), следующие:
 ;
; ![]() (5)
(5)
Приведенные на рис. 1 системные взаимосвязи полевых ФВ с «материальными» электромагнитными величинами показывают принципиальную возможность описания электромагнитных закономерностей, в том числе для электромагнитных волн в вакууме, без использования полевых величин. Рассмотрим, как при этом изменятся привычные закономерные соотношения, в которых применялись полевые ФВ. Изображения новых закономерных соотношений будем для наглядности показывать в системе ФВиЗ.
На рис. 2 показаны изображения системных закономерностей, представленных математическими выражениями (1) и (2), а на рис. 3 показаны изображения системных закономерностей, представленных выражениями (3) и (4). На рис. 2 системные закономерности представлены выделенными параллелограммами, а на рис. 3 – выделенными линиями (когда параллелограмм смотрится как бы сбоку, в проекции на плоскость, перпендикулярную плоскости выделенного параллелограмма).
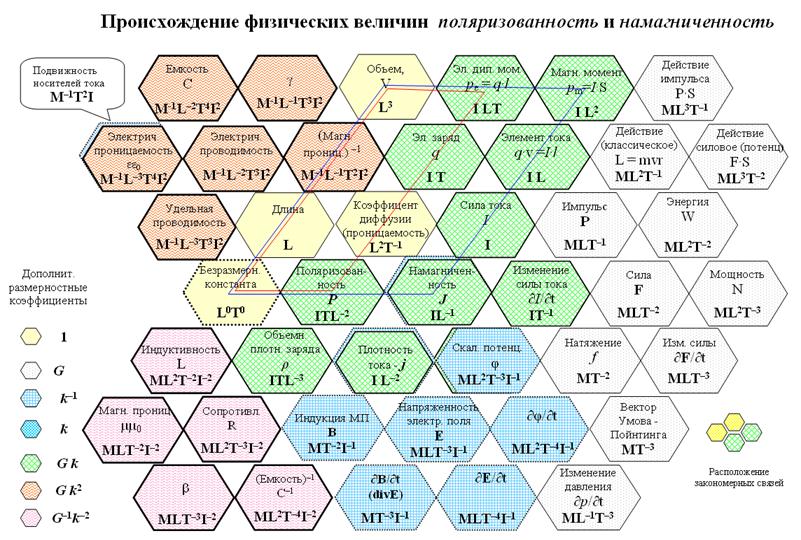
Рис. 2. Поляризованность и намагниченность в системе ФВиЗ

Рис. 3. Системное представление объемной плотности электрической и магнитной энергий без использования полевых параметров
На данных рисунках – схемах хорошо видно структурное деление электромагнитных величин на системные группы и подгруппы, которые выделены различными цветами. Надо иметь в виду, что ФВ в системе располагаются многослойно и могут «накладываться» друг на друга. По этой причине их на одной плоской картинке невозможно отобразить, поэтому приходится пользоваться несколькими изображениями-сечениями системы.
Исходя из известного равенства амплитудных значений энергии электрической и магнитной составляющих электромагнитной волны, можно определить соотношения между амплитудными значениями поляризованности и намагниченности:
 ,
,  . (6)
. (6)
Откуда следует:
 . (7)
. (7)
Обозначения всех составляющих этих выражений приводились выше; добавление индекса max означает максимальное значение; с - скорость света.
Выражение (7) определяет соотношение между максимальными значениями поляризованности и намагниченности вакуума в электромагнитной волне. Они оказываются связанными через скорость света с.
Приведенные изображения системных закономерностей и математические формулы показывают, что без полевых величин напряженность электрического поля и индукция магнитного поля при описании электромагнитных волн можно обойтись. «Не множьте сущностей без крайней необходимости!» - принцип известный и его вполне можно применить в электродинамике, полностью отказавшись от использования полевых электромагнитных величин.
Приводимые рисунки-схемы позволяют легко обнаружить и иные системные взаимосвязи поляризованности и намагниченности с другими величинами, которыми характеризуются электромагнитные волны. Например, объемная плотность энергии волны определится соотношением:
 , (8)
, (8)
где: ![]() - электрическая проводимость вакуума;
- электрическая проводимость вакуума; ![]() и
и ![]() - средние значения модулей векторов
- средние значения модулей векторов ![]() и
и ![]() . Здесь приняты средние значения модулей векторов потому, что объемная плотность энергии имеет вполне определенное значение, а сами модули векторов изменчивы и поочередно могут (и должны) принимать нулевые значения.
. Здесь приняты средние значения модулей векторов потому, что объемная плотность энергии имеет вполне определенное значение, а сами модули векторов изменчивы и поочередно могут (и должны) принимать нулевые значения.
Возможные оппоненты излагаемой точки зрения на возможность описания электромагнитных закономерностей без полевых величин могут сослаться на необходимость их применения в описании силовых взаимодействий с участием электрического заряда. Но такое описание возможно и без привлечения полевых величин, что наглядно показано на рис.4. На этом же рисунке приведена системная закономерность, показывающая (или предсказывающая) наличие силового воздействия на электрические заряды (параллелограмм синего цвета) при участии намагниченности и структуро-средовой ФВ проводимость.
На рис. 5 показаны системные закономерности, иллюстрирующие волновые соотношения электромагнитных величин без привлечения полевых ФВ.
Показанная пунктиром системная закономерность с участием вектора Умова-Пойнтинга ![]() явно указывает на ее принадлежность к волновому описанию, хотя в ней и не содержится полевых величин. Математическое выражение этой закономерности для вакуума следующее:
явно указывает на ее принадлежность к волновому описанию, хотя в ней и не содержится полевых величин. Математическое выражение этой закономерности для вакуума следующее:
 . (9)
. (9)

Рис. 4. Системные силовые взаимосвязи с участием электрического заряда, поляризованности и намагниченности
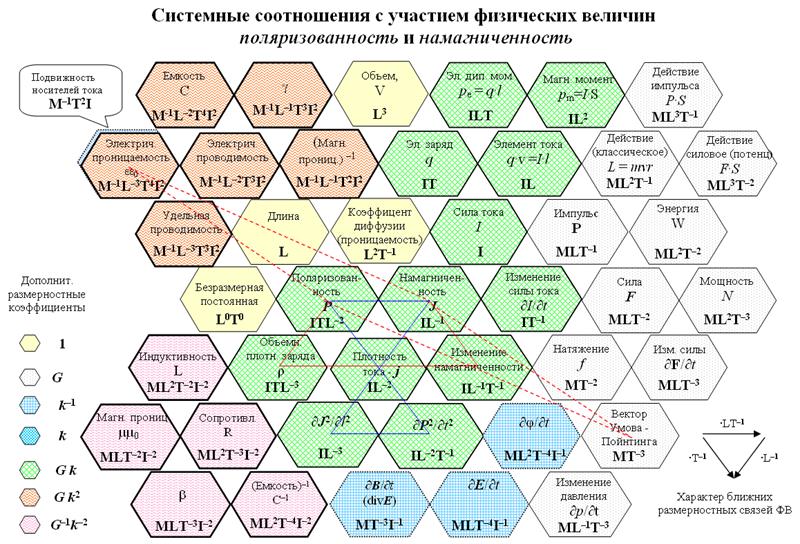
Рис. 5. Системные взаимосвязи, иллюстрирующие волновые соотношения
Из приводимых на рис. 5 системных взаимосвязей с участием ФВ поляризованность и намагниченность можно составить следующие математические соотношения (для вакуума):
 , (10)
, (10)
 , (11)
, (11)
 . (12)
. (12)
Соотношения (10) – (12) (без правых штрихованных частей) для мгновенных значений поляризованности и намагниченности, по сути, представляют собой линейные волновые уравнения первой степени.
Исходя из системных соотношений ФВ, показанных на рис.5, можно также составить общее волновое уравнения второй степени, используемое для описания как бегущих, так и стоячих волн:
 , (13)
, (13)
где: ![]() - оператор Лапласа.
- оператор Лапласа.
Отличие приводимых волновых уравнений от общепринятых записей подобных волновых уравнений состоит в том, что они содержат два изменяющихся параметра (![]() и
и ![]() ), а не один полевой, как это обычно принято. Использование в волновых уравнениях не полевых, а «материальных» величин поляризованность и намагниченность вакуума создает, по мнению автора, предпосылки успешной разработки наглядной физической модели-представления для электромагнитной волны. При этом изменения поляризованности и намагниченности возможно будет представить не синфазно меняющимися, как это изображается для векторов Е и В в бегущих электромагнитных волнах, а со сдвигом по фазе на четверть периода, что более естественно для описания волновых и колебательных процессов. Пример такого упрощенного модельного изображения электромагнитной волны приводится в работе К.Б. Канна [5].
), а не один полевой, как это обычно принято. Использование в волновых уравнениях не полевых, а «материальных» величин поляризованность и намагниченность вакуума создает, по мнению автора, предпосылки успешной разработки наглядной физической модели-представления для электромагнитной волны. При этом изменения поляризованности и намагниченности возможно будет представить не синфазно меняющимися, как это изображается для векторов Е и В в бегущих электромагнитных волнах, а со сдвигом по фазе на четверть периода, что более естественно для описания волновых и колебательных процессов. Пример такого упрощенного модельного изображения электромагнитной волны приводится в работе К.Б. Канна [5].

Рис. 6. Изображение электромагнитной волны по Канну
На рис. 6 ясно представлено как происходит формирование электрической составляющей электромагнитной волны в виде динамического электрического диполя из противоположно заряженных пар виртуальных частиц и смещение по фазе на четверть периода токовой составляющей, формирующей магнитную составляющую волны. При этом Канн в своих работах придерживается традиционного описания электромагнитных волн.
Предлагаемое в настоящей работе описание электромагнитных волн с использованием физических величин поляризованность и намагниченность больше подходит для модельного изображения волны по рис. 6. Правда вопрос о направленности вектора намагниченности в волне остается не совсем ясным. В физических опытах известен эффект Фарадея ([5], с. 219) – вращение плоскости поляризации электромагнитной волны при распространении ее вдоль магнитных силовых линий. Дальнейшее изучение этого эффекта может дать новые представления о строении электромагнитных волн.
Далее в табличной форме приведены основные соотношения, описывающие отдельные параметры и различные возможные соотношения для электромагнитных волн вакуума с участием полевых физических величин и без их участия.
Таблица.
Наименование параметра или соотношения | Полевая форма представления | Возможные соотношения с участием «материальных» ФВ |
Взаимосвязь полевых ФВ с «материальными» электромагнитными величинами |
| |
Объемная плотность электрической энергии |
|
|
Объемная плотность магнитной энергии |
|
|
Объемная плотность электромагнитной энергии | От 0 до |
|
Вектор Умова-Пойнтинга |
|
|
Соотношения между разнотипными изменяющимися величинами |
для волн в вакууме |
для волн в вакууме |
|
| |
|
| |
|
| |
|
| |
|
| |
Одномерное волновое уравнение с первыми производными |
|
|
Одномерные волновые уравнения с вторыми производными |
|
|
Соотношения между амплитудными значениями разнотипных величин |
|
|
В таблице дополнительным подстрочным индексом В обозначены параметры, соответствующие вакууму. Другие обозначения: с – скорость света; ![]() ,
,![]() и
и ![]() - токи смещения, разные по происхождению (см. таблицу);
- токи смещения, разные по происхождению (см. таблицу); ![]() - волновая проводимость вакуума.
- волновая проводимость вакуума.
Надо отметить, что выражение отдельных полевых электромагнитных параметров через «материальные» ФВ встречается и у других авторов. Так, например, в работе [6] вектор D - индукции электрического поля трактуется как объемная плотность поляризованности материальной среды. Наш подход более широкий, он предусматривает полный отказ от использования полевых величин - как менее информативных, без которых при описании электромагнитных процессов можно обойтись.
Выводы
1. С привлечением системы физических величин и закономерностей показана возможность описания электромагнитных волн в вакууме с применением «материальных» физических величин поляризованность и намагниченность.
2. Применение физических величин поляризованность и намагниченность для описания электромагнитных волн создает возможность их модельного представления и обнаружения механизма взаимных превращений в волне электрической и магнитной энергий.
Литература
1. Чуев А.С. Системный подход в физическом образовании инженеров // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 2. Режим доступа: http://technomag.edu.ru/doc/299700.html(дата обращения 08.07.2012).
2. Чуев А.С. Система физических величин и закономерных размерностных взаимосвязей между ними // Законодательная и прикладная метрология. 2007. №3. С. 30-33.
3. Википедия. Поляризация вакуума. Режим доступа:http://ru.wikipedia.org/wiki/Поляризация_вакуума(дата обращения 08.07.2012).
4. Канн К.Б. Электромагнитные волны. Режим доступа: http://electrodynamics.narod.ru/em-waves.html(дата обращения 08.07.2012).
5. Иродов И.Е. Волновые процессы. Основные законы: учеб. пособие для вузов. – 2-е изд., доп. – М.: БИНОМ. Лаборатория знаний, 2004. – 263 с.
6. Макаров А.М., Лунёва Л.А., Макаров К.А. Об основных уравнениях электростатики изотропных диэлектриков // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2011. №2. С. 25-40.
6. Макаров А.М., Лунёва Л.А., Макаров К.А. Об основных уравнениях электростатики изотропных диэлектриков. – Вестник МГТУ им. Н.Э. Баумана. Серия «Естественные науки». – М.: МГТУ им. Н.Э. Баумана, 2011. - №2. С. 25-40.
Публикации с ключевыми словами: электромагнитные волны, волновые уравнения, система физических величин, физические законы, система физических законов
Публикации со словами: электромагнитные волны, волновые уравнения, система физических величин, физические законы, система физических законов
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||