научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2012
DOI: 10.7463/0612.0423297
УДК 778.35:629.7
Россия, МГТУ имени Н.Э. Баумана
Введение
В конце 90-х годов ХХ в. начался новый этап развития инфракрасных систем (ИКС), что было вызвано, в первую очередь, заметным совершенствованием и, как следствие, расширением применения двумерных (матричных) многоэлементных приемников излучения (МПИ), позволяющих реализовать методы электронного сканирования и пространственной выборки инфракрасных изображений, т.е. отказаться от оптико-механических сканирующих устройств. Опрос отдельных элементов МПИ с последующей обработкой получаемых при этом электрических сигналов принято называть «смотрящим» режимом работы, а сами системы – системами «смотрящего» типа.
Наряду с созданием МПИ высокого разрешения и большого формата на развитие ИКС «смотрящего» типа заметное влияние оказало и оказывает разработка новых полноформатных ПЗС и КМОП-схем считывания и первичной обработки сигналов с отдельных элементов МПИ. Пространственное разрешение таких систем в настоящее время приближается к разрешению оптико-электронных систем видимого диапазона.
Оценка разрешающей способности оптико-электронных систем (ОЭС) с использованием аналитического метода является одним из перспективных направлений их исследования. Она не только позволяет проводить сравнительную оценку разнотипных ОЭС но и помогает формировать научно-техническую политику (направление) их развития (планировать распределение сил и средств при разработке стратегии развития).
Основа современного анализа качества изображения – теория линейной фильтрации (суть аналитического способа оценки разрешающей способности). Она является частью Фурье анализа – анализа, используемого для изучения реакции на сигнал линейных инвариантных устойчивых систем.
Процесс прохождения информации в инфракрасных системах условно может быть представлен в виде системы последовательного соединения отдельных передаточных звеньев. В каждое звено системы вкладывается свое физическое содержание, однако, общим для всех звеньев является то, что каждое звено оказывает свое влияние на сигнал, несущий информацию, и это влияние рассматривается независимо от других звеньев. Каждое звено инфракрасной системы (ИКС) дистанционного зондирования Земли (ДЗЗ) описывается своей оптической передаточной функцией (ОПФ). Оптическая передаточная функция является комплексной величиной, характеризующей способность системы изображения воспроизводить пространственные частоты, содержащиеся в спектре частот объекта. Модуль ОПФ, представляющий собой амплитуду реакции системы на синусоидальное распределение, называется функцией передачи модуляции (ФПМ). Результирующая ФПМ ИК-системы находится как произведение ФПМ отдельных звеньев системы.
Угловое (пространственное) разрешение в настоящее время является наиболее часто используемым критерием качества изображения, а следовательно и параметром контроля технического состояния ИКС. Достоинством этого критерия является его хорошая корреляция с вероятностью распознавания объектов. Согласно, аналитического метода определения разрешающей способности ИКС [1, 2], она определяется, как абсцисса пересечения двух функций: результирующей ФПМ ИКС и пороговой модуляционной характеристики.
Таким образом, для определения предельной пространственной частоты
необходимо найти первый корень нелинейного уравнения
![]() ,
,
где ![]() ФПМ ИКС,
ФПМ ИКС, ![]() пороговая модуляционная характеристика,
пороговая модуляционная характеристика, ![]() пространственная частота,
пространственная частота, ![]() - разрешающая способность ИКС,
- разрешающая способность ИКС,  - угловое разрешение ИКС,
- угловое разрешение ИКС,
 .
.
Здесь ![]() коэффициент пропускания атмосферы,
коэффициент пропускания атмосферы, ![]() энергетическая яркость объекта,
энергетическая яркость объекта, ![]() энергетическая яркость фона,
энергетическая яркость фона, ![]() энергетическая яркость дымки.
энергетическая яркость дымки.
Использование аналитического метода оценки характеристик ИКС так же позволяет осуществить оценку эффективности их применения при решении специальных задач в различных условиях.
Вывод пороговой модуляционной характеристики «Цифровая инфракрасная система - дешифровщик» на основе теории оптимального обнаружения
Одной из важных зависимостей, применяемых при оценке пространственного разрешения инфракрасных средств, является пороговая модуляционная характеристика (ПМХ). ПМХ – это характеристика, оценивающая шумовые свойства системы и глаза наблюдателя. Она представляет собой пороговый контраст теплового изображения штриховой миры, который еще распознается (визуально или автоматически) при заданной пространственной частоте. Определение ПМХ можно связать с задачей обнаружения факта наличия модуляции сигнала.
До недавнего времени ИКС ДЗЗ были представлены широким классом технических систем, элементом регистрации и отображения информации, у которых являлась фотопленка. Задача нахождения аналитического выражения ПМХ для систем такого класса решена. С появлением цифровых ИКС вопрос получения аналитического вида ПМХ, для оценки эффективности этих средств, стоит остро. В данном параграфе уделено внимание решению этого вопроса.
Выходной сигнал – это ИК-изображение, наблюдаемое оператором-дешифровщиком на мониторе. При этом на сигнал накладываются шумы, вносимыми электронной схемой считывания и приемника излучения [3, 4]. Кроме того, при визуальном восприятии действует шум зрительного анализатора, обусловленный флуктуацией возбуждения в зрительной системе человека [5]. Поэтому имеет смысл вычисление пороговой модуляции – предельной модуляции выходного сигнала, когда она еще наблюдается на фоне шумов с заданной вероятностью.
Рассмотрим характеристики шумов изображения.
Наиболее полной характеристикой шума является автокорреляционная функция
 ,
,
где ![]() площадь изображения, по которой выполняется интегрирование,
площадь изображения, по которой выполняется интегрирование, ![]() световое ощущение глаза изображения,
световое ощущение глаза изображения,  - среднее световое ощущение глаза изображения,
- среднее световое ощущение глаза изображения, ![]() и
и ![]() - расстояния по осям
- расстояния по осям ![]() и
и ![]() соответственно между точками изображения, на которых рассчитывается корреляционная связь [6].
соответственно между точками изображения, на которых рассчитывается корреляционная связь [6].
По автокорреляционной функции вычисляется спектральная плотность (энергетический спектр) шумов изображения ![]() .
.
 ,
,
где ![]() – пространственные частоты по осям x и yсоответственно.
– пространственные частоты по осям x и yсоответственно.
Особый интерес представляет постоянная составляющая спектра ![]() (при
(при ![]() ). Геометрический смысл
). Геометрический смысл ![]() - объем фигуры, ограниченной поверхностью
- объем фигуры, ограниченной поверхностью ![]() и плоскостью
и плоскостью ![]() , физический смысл – энергия шума.
, физический смысл – энергия шума.
Одной из характеристик шума является его радиус корреляции [7]. При этом ![]() как бы заменяется цилиндрической поверхностью, высота которой равна
как бы заменяется цилиндрической поверхностью, высота которой равна ![]() , а в основании – эллипс, площадь которого
, а в основании – эллипс, площадь которого ![]() такая, что выполняется равенство
такая, что выполняется равенство ![]() . По форме эллипс подобен фигуре, получаемой при сечении
. По форме эллипс подобен фигуре, получаемой при сечении ![]() плоскостью, параллельной
плоскостью, параллельной ![]() . Площадь
. Площадь ![]() называется площадью корреляции. Если характеристики шума одинаковы по
называется площадью корреляции. Если характеристики шума одинаковы по ![]() и по
и по ![]() , то сечение
, то сечение ![]() – круг, и
– круг, и ![]() , здесь
, здесь ![]() называют радиусом корреляции. Таким образом, можно записать
называют радиусом корреляции. Таким образом, можно записать
 .
.
Для расчета энергии шума необходимо знать его радиус корреляции ![]() и дисперсию
и дисперсию ![]() .
.
Для определения пороговой модуляционной характеристики необходимо описать деятельность дешифровщика при наблюдении пространственных гармонических сигналов (ПГС) на разных частотах.
Задачей дешифровщика является обнаружение факта наличия модуляции сигнала. Будем считать, что дешифровщик работает как оптимальный линейный фильтр, модель которого представлена на рисунке 1.
В процессе дешифрирования оператор использует увеличение миры путем масштабирования оцифрованного изображения. Пусть минимальная частота наблюдаемого сигнала ![]() . Тогда наблюдается
. Тогда наблюдается ![]() периодов ПГС. При наблюдении частоты
периодов ПГС. При наблюдении частоты ![]() используется увеличение
используется увеличение ![]() , тогда наблюдаемая частота будет тоже
, тогда наблюдаемая частота будет тоже ![]() , но изображение увеличено, а, следовательно, увеличен радиус корреляции шумов в
, но изображение увеличено, а, следовательно, увеличен радиус корреляции шумов в ![]() раз, т.е.
раз, т.е.
 ,
,
где ![]() наблюдаемый радиус корреляции шумов.
наблюдаемый радиус корреляции шумов.
Пусть дешифровщик наблюдает изображение миры как квадрат со стороной ![]() (рисунок 2).
(рисунок 2).

Рисунок 1 – Модель дешифровщика
Итак, возможны 2 ситуации:
1. В предъявленном изображении имеется модуляция, т.е.
![]() ,
,
где ![]() ˗ световое ощущение глаза изображения ПГС,
˗ световое ощущение глаза изображения ПГС, ![]() переменная составляющая
переменная составляющая ![]() ,
, ![]() составляющая светового ощущения глаза изображения, обусловленная шумами,
составляющая светового ощущения глаза изображения, обусловленная шумами, ![]() среднее значение светового ощущения глаза изображения.
среднее значение светового ощущения глаза изображения.

Рисунок 2 - Фрагмент штриховой инфракрасной миры
2. В предъявленном изображении модуляция отсутствует
![]() ,
,
Получаемый на выходе фильтра сигнал может быть рассчитан по формуле


где ![]() составляющая выходного сигнала фильтра, обусловленная наличием модуляции в изображении,
составляющая выходного сигнала фильтра, обусловленная наличием модуляции в изображении, ![]() составляющая выходного сигнала, обусловленная шумами. Найдем ее характеристики при условии, что
составляющая выходного сигнала, обусловленная шумами. Найдем ее характеристики при условии, что ![]() , где
, где ![]() некоторая константа, а
некоторая константа, а ![]() .
.
Математическое ожидание

 ,
,
так как  и
и ![]() .
.
Второй момент



 .
.
Последний интеграл можно привести к следующему виду


Так как радиус корреляции ![]() шума
шума ![]() значительно меньше
значительно меньше ![]() , то на
, то на ![]() можно принять
можно принять ![]() . С учетом стационарности шума
. С учетом стационарности шума ![]() можно записать
можно записать ![]() и упростить интеграл
и упростить интеграл


Последнее приближенное равенство записано с учетом, что ![]() значительно меньше
значительно меньше ![]() [8], поэтому изменение пределов интегрирования
[8], поэтому изменение пределов интегрирования ![]() до бесконечных мало изменит результат.
до бесконечных мало изменит результат.
Оценим энергию части выходного сигнала фильтра ![]() обусловленной наличием модуляции
обусловленной наличием модуляции
 .
.
Необходимо выбрать ![]() такую, чтобы доставляла максимум
такую, чтобы доставляла максимум ![]() . Известно, что
. Известно, что  , которое выполняется как равенство, если
, которое выполняется как равенство, если ![]() , где
, где ![]() константа. Следовательно, это и есть условие максимума
константа. Следовательно, это и есть условие максимума ![]() .
.
Физический смысл: дешифровщик строит мысленный образ сигнала, который он должен обнаружить. Поскольку вид сигнала ему известен, то мысленный образ ![]() соответствует обнаруживаемому сигналу
соответствует обнаруживаемому сигналу ![]() .
.
Доказано [9], что наименьшая ошибка обнаружения соответствует максимуму отношения сигнал/шум ![]() :
:
 ,
,
или в развернутом виде
 .
.
Если ![]() , а
, а  , то
, то
 (3.3)
(3.3)
или 
где  - составляющая сигнала на выходе фильтра, обусловленная наличием модуляции,
- составляющая сигнала на выходе фильтра, обусловленная наличием модуляции, ![]()
 -СКО составляющей сигнала на выходе фильтра, обусловленная действием шумов
-СКО составляющей сигнала на выходе фильтра, обусловленная действием шумов ![]() .
.

Рисунок 3 - Световое ощущение глаза ![]() изображения фрагмента миры
изображения фрагмента миры
Вычислим значение ![]() полезной составляющей сигнала. для этого воспользуемся рисунком 3. Выражение для
полезной составляющей сигнала. для этого воспользуемся рисунком 3. Выражение для ![]() имеет вид (т.к. это ПГС) на
имеет вид (т.к. это ПГС) на ![]()
 ,
,
а  ,
, ![]()
где ![]() число периодов сигнала, уместившихся на длине
число периодов сигнала, уместившихся на длине ![]() . Значение интеграла
. Значение интеграла ![]() принимает вид
принимает вид

 .
.
Выражение в знаменателе преобразуем следующим образом
 .
.
Очевидно, зная спектральную плотность шума ![]() того источника
того источника ![]() и передаточную функцию
и передаточную функцию ![]() ИКС, можно найти спектральную плотность шума на выходе этой системы [10] как
ИКС, можно найти спектральную плотность шума на выходе этой системы [10] как
 ,
,
где ![]() ,
, ![]() ;
; ![]() пространственные частоты в плоскости приемника излучения.
пространственные частоты в плоскости приемника излучения.
Учитывая, что

Энергия шума
![]()
Спектральная плотность связана с корреляционной функцией через преобразование Фурье

Поэтому
 ,
,
где ![]() значение спектральной плотности шума на нулевой частоте.
значение спектральной плотности шума на нулевой частоте.
Так, например, если рассматривается тепловое изображение на экране видеоконтрольного устройства формируемое цифровой ИКС, то, принимая шумы зрительного аппарата дешифровщика, фотонный шум, тепловой шум Джонсона, избыточный шум, генерационно-рекомбинационный шум, шумы электронной схемы считывания, шумы приемника излучения и шумы видеоконтрольного устройства ВКУ некоррелированными, а также приводя значения спектральной плотности фотонного шума, теплового шума Джонсона, избыточного шума, генерационно-рекомбинационных шума, шумов электронной схемы считывания, шумов приемника излучения и видео-контрольного устройства ВКУ к глазу с учетом,

где, ![]() световое ощущение глаза;
световое ощущение глаза;
![]() тангенс угла наклона логарифмической зависимости между световым ощущением глаза
тангенс угла наклона логарифмической зависимости между световым ощущением глаза ![]() и наблюдаемой яркостью
и наблюдаемой яркостью ![]() .
.
![]() яркость изображения на экране ВКУ переменной составляющей сигнала;
яркость изображения на экране ВКУ переменной составляющей сигнала;
![]() средняя яркость изображения на экране ВКУ.
средняя яркость изображения на экране ВКУ.
То можно записать

![]()

![]()
где, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() соответственно корреляционная функция, радиус корреляции и СКО шумов зрительного анализатора, фотонного шума, теплового шума Джонсона, избыточного шума, генерационно-рекомбинационного шума, шумов электронной схемы считывания, шумов приемника излучения и ВКУ.
соответственно корреляционная функция, радиус корреляции и СКО шумов зрительного анализатора, фотонного шума, теплового шума Джонсона, избыточного шума, генерационно-рекомбинационного шума, шумов электронной схемы считывания, шумов приемника излучения и ВКУ.
Однако необходимо еще учесть изменение масштаба, т.е. формулу для наблюдаемого радиуса корреляции
 .
.
Теперь можно вычислить выражение для амплитуды переменной составляющей сигнала ![]() , обеспечивающей отношение сигнал/шум
, обеспечивающей отношение сигнал/шум


или с учетом
 .
.
Для определения пороговой модуляционной характеристики (ПМХ) ![]() необходимо перейти от модуляции по световому ощущению к модуляции по экспозиции
необходимо перейти от модуляции по световому ощущению к модуляции по экспозиции
![]() ,
,
где ![]() яркость экрана
яркость экрана
![]() и
и ![]() переменная и постоянная составляющая сигнала
переменная и постоянная составляющая сигнала
Если ![]() мало по сравнению с
мало по сравнению с ![]() , то
, то
 .
.
Так как матрица приемника ИК-излучения - линейное звено [11], и видеоконтрольное устройство (ВКУ) можно принять линейным звеном, тогда
![]() ,
, ![]() ,
,
где ![]() коэффициент контрастности системы цифровая ИКС-ВКУ.
коэффициент контрастности системы цифровая ИКС-ВКУ.
Очевидно, что  , следовательно справедливо выражение
, следовательно справедливо выражение
 .
.
Если ![]() амплитуда переменной составляющей ПГС на частоте
амплитуда переменной составляющей ПГС на частоте ![]() , а
, а ![]() его постоянная составляющая, то модуляция этого сигнала, которая называется пороговой модуляционной характеристикой
его постоянная составляющая, то модуляция этого сигнала, которая называется пороговой модуляционной характеристикой

 .
.
Следует отметить, что ПМХ в данном случае зависит от отношения сигнал/шум.
Выберем правило вычисления величины ![]() по заданной вероятности ошибки (критерий идеального наблюдателя).
по заданной вероятности ошибки (критерий идеального наблюдателя).
На выходе фильтра ![]() (рисунок 2) имеется выходной сигнал
(рисунок 2) имеется выходной сигнал ![]() , который содержит или не содержит информацию
, который содержит или не содержит информацию ![]() о наличии модуляции. Для принятия решения о наличии или отсутствии модуляции назначается
о наличии модуляции. Для принятия решения о наличии или отсутствии модуляции назначается ![]() пороговое значение сигнала (рисунок 4).
пороговое значение сигнала (рисунок 4).

Рисунок 4 - Плотности распределения выходного сигнала
В дальнейшем, если ![]() , принимается решение о наличии модуляции, в противном случае – о ее отсутствии.
, принимается решение о наличии модуляции, в противном случае – о ее отсутствии.
Если шум ![]() принять нормально распределенными, то и сигнал
принять нормально распределенными, то и сигнал ![]() , как линейное преобразование шума
, как линейное преобразование шума ![]() , будет иметь нормальное распределение с параметрами
, будет иметь нормальное распределение с параметрами ![]() и
и ![]() .
.
В этом случае плотность распределения сигнала ![]() будет
будет

После назначения порога ![]() вероятность ошибки
вероятность ошибки ![]() будет равна
будет равна

где, ![]() и
и ![]() - априорные вероятности отсутствия и наличие модуляции, будем считать их равными, т.е.
- априорные вероятности отсутствия и наличие модуляции, будем считать их равными, т.е. ![]() .
.
Определив минимум ![]() по
по ![]() , найдем условие для вычисления порога
, найдем условие для вычисления порога ![]() :
:
![]() ,
,
Так как ![]() симметричная, т.е.
симметричная, т.е. ![]() , нетрудно видеть, что
, нетрудно видеть, что  .
.
Тогда

 ,
,
где  интеграл вероятностей.
интеграл вероятностей.
Следовательно, можно записать
 .
.
Таким образом, окончательное выражение для ПМХ принимает вид
 ,
,
где ![]() пороговая модуляция глаза (Принято считать
пороговая модуляция глаза (Принято считать ![]() ),
),  квадратный корень отношение площади корреляции шумов, вызванных флуктуациями нервного возбуждения к площади наблюдаемого фрагмента,
квадратный корень отношение площади корреляции шумов, вызванных флуктуациями нервного возбуждения к площади наблюдаемого фрагмента, ![]() коэффициент, учитывающий допустимую вероятность ошибки.
коэффициент, учитывающий допустимую вероятность ошибки.
Таким образом, пороговая модуляционная характеристика ИКС определяется фотонным шумом ![]() , тепловым шумом Джонсона
, тепловым шумом Джонсона ![]() , избыточным шумом
, избыточным шумом ![]() , генерационно-рекомбинационным шумом
, генерационно-рекомбинационным шумом ![]() , шумами электрической схемы считывания
, шумами электрической схемы считывания ![]() , шумами приемника излучения
, шумами приемника излучения ![]() , видеоконтрольного устройства
, видеоконтрольного устройства ![]() , а также пороговой модуляцией глаза
, а также пороговой модуляцией глаза ![]() , отношением сигнал/шум при заданной вероятности ошибки
, отношением сигнал/шум при заданной вероятности ошибки ![]() , средней яркостью изображения на экране ВКУ
, средней яркостью изображения на экране ВКУ ![]() и величиной тангенса угла наклона логарифмической зависимости между световым ощущением глаза и наблюдаемой яркостью
и величиной тангенса угла наклона логарифмической зависимости между световым ощущением глаза и наблюдаемой яркостью ![]() .
.
Функция передачи модуляции цифровой инфракрасной системы дистанционного зондирования Земли
Исходя из конструктивных особенностей рассматриваемой цифровой ИКС запишем формулу для результирующей ФПМ:
![]()
где ![]() ФПМ атмосферы,
ФПМ атмосферы, ![]() ФПМ дифракционного объектива,
ФПМ дифракционного объектива, ![]() системы фокусировки,
системы фокусировки, ![]() ФПМ вибраций фотоустановки,
ФПМ вибраций фотоустановки, ![]() ФПМ видеоусилителя,
ФПМ видеоусилителя, ![]() ФПМ сдвига изображения,
ФПМ сдвига изображения, ![]() ФПМ приемника излучения с предварительным усилителем;
ФПМ приемника излучения с предварительным усилителем; ![]() ФПМ видеоконтрольного устройства
ФПМ видеоконтрольного устройства
Функция передачи модуляции атмосферы:
Функция передачи модуляции атмосферы имеет следующий вид:
![]()
![]() ФПМ, учитывающая турбулентность атмосферы определяется по формуле:
ФПМ, учитывающая турбулентность атмосферы определяется по формуле:
![]()
где ![]() коэффициент турбулентности атмосферы;
коэффициент турбулентности атмосферы;
![]() фокусное расстояние;
фокусное расстояние;
![]() пространственная частота;
пространственная частота;
Уточним значения коэффициента ![]() в различных условиях, таблица 1. составлена по данным и их аппроксимации.
в различных условиях, таблица 1. составлена по данным и их аппроксимации.
Таблица 1 - Зависимость коэффициента турбулентности атмосферы от высоты
Турбулентность | Значения | ||
до 1700 м | от 1700 до 10000 м | Более 10000 м | |
слабая | 2,5∙10-6 | (2,7-H∙10-4)∙10-6 | 0,017/H |
сильная | 2,5∙10-5 | (2,9-2∙H∙10-4)∙10-6 | 0,1/H |
![]() ФПМ дымки (рисунок 5) выводится следующим образом
ФПМ дымки (рисунок 5) выводится следующим образом

 ,
,  ,
, ,
,
 ,
,  ,
,
![]() ,
,
где ![]() наложенный контраст,
наложенный контраст, ![]() яркость объекта,
яркость объекта, ![]() яркость фона,
яркость фона, ![]() яркость дымки,
яркость дымки, ![]() коэффициент пропускания излучения атмосферой и аппроксимирующая функция, получены из математической модели атмосферы Lowtran7,
коэффициент пропускания излучения атмосферой и аппроксимирующая функция, получены из математической модели атмосферы Lowtran7, ![]() энергетическая светимость по закону Планка,
энергетическая светимость по закону Планка, ![]() константы Планка.
константы Планка.

Рисунок 5 - К определению ФПМ атмосферы (учет турбулентности и дымки)
ФПМ дифракционного объектива описывается формулой:

где ![]() нижняя и верхняя границы волнового инфракрасного диапазона в котором работает ИКС,
нижняя и верхняя границы волнового инфракрасного диапазона в котором работает ИКС, ![]() диафрагменное число,
диафрагменное число, ![]() пространственная частота в плоскости приемника излучения.
пространственная частота в плоскости приемника излучения.
Зависимость ФПМ дифракционного объектива ![]() от диафрагменного числа
от диафрагменного числа ![]() показана на рисунке 6,
показана на рисунке 6, ![]() функции передачи дифракционного объектива соответственно при
функции передачи дифракционного объектива соответственно при ![]() =2,5 ;4, 11.
=2,5 ;4, 11.

Рисунок 6 - Зависимость ФПМ дифракционного объектива ![]() от диафрагменного числа
от диафрагменного числа ![]()
Анализ представленных зависимостей показывает, что значения ФПМ дифракционного объектива снижаются при увеличении значений диафрагменного числа, например в случае когда диафрагменное число ![]() повышается с 2,5 до 4 значения ФПМ снижаются на 30 %.
повышается с 2,5 до 4 значения ФПМ снижаются на 30 %.
ФПМ вибраций цифровой ИКС на фотоустановке
Функция передачи модуляции вибраций цифровой ИКС на аэрофотоустановке (рисунок 7) вычисляется аналогично ФПМ турбулентной атмосферы и имеет вид:
![]() ,
,
где ![]() - параметр функции рассеяния точки, обусловленный вибрациями цифровой ИКС;
- параметр функции рассеяния точки, обусловленный вибрациями цифровой ИКС; ![]() фокусное расстояние;
фокусное расстояние;

Рисунок 7 - ФПМ вибраций фотоустановки
ФПМ системы фокусировки выглядит следующим образом:
 ,
,
где ![]() - фокусное расстояние,
- фокусное расстояние, ![]() - погрешность фокусировки,
- погрешность фокусировки, ![]() диаметр входного отверстия объектива.
диаметр входного отверстия объектива.
При исследовании математической модели цифровой ИКС была получена явная зависимость между погрешностью системы фокусировки ![]() и такой характеристикой, как угловое разрешение
и такой характеристикой, как угловое разрешение ![]() . Ее характер можно пронаблюдать как в таблице 2. так и на рисунке 8. Исследования можно представить и графически рисунок 9, что сделано для крайних членов таблицы 2, где
. Ее характер можно пронаблюдать как в таблице 2. так и на рисунке 8. Исследования можно представить и графически рисунок 9, что сделано для крайних членов таблицы 2, где ![]() функция передачи модуляции от расфокусировки соответственно при
функция передачи модуляции от расфокусировки соответственно при ![]() 0,05; 0,1; 0,15.
0,05; 0,1; 0,15.
Причинами возникновения расфокусировки![]() может быть перепад температур и давлений. А отсюда, как следствие, достижение температурой и давлением значений, при которых деформация конструктивных материалов уже существенна.
может быть перепад температур и давлений. А отсюда, как следствие, достижение температурой и давлением значений, при которых деформация конструктивных материалов уже существенна.
Таблица 2 - Зависимость углового разрешения цифровой ИКС, от расфокусировки ![]() при скорости полёта
при скорости полёта ![]() =800 км/ч и высоте
=800 км/ч и высоте ![]() =1000 м
=1000 м
| 0,05 | 0,1 | 0,15 | 0,2 | 0,25 |
| 1,323 | 1,389 | 1,493 | 1,63 | 1,792 |
Анализ результатов исследования зависимости углового разрешения ![]() от погрешности системы фокусировки, представленных на графике рисунок 8, показывает, что при изменении величины расфокусировки
от погрешности системы фокусировки, представленных на графике рисунок 8, показывает, что при изменении величины расфокусировки ![]() от 0,05 до 0,25 мм угловое разрешение цифровой ИКС падает на 26 %.
от 0,05 до 0,25 мм угловое разрешение цифровой ИКС падает на 26 %.

Рисунок 8 - Влияние погрешности системы фокусировки на разрешающую способность цифровой ИКС, имеющей с МПИ размером 320х240 пикселей

Рисунок 9 – Функции передачи модуляции цифровой ИКС при различных значениях расфокусировки ![]() 0,05; 0,1; 0,15
0,05; 0,1; 0,15
Таким образом, для цифровых ИКС имеющих малые значения фокусного расстояния (для исследуемой, цифровой ИКС ![]() мм) погрешность расфокусировки необходимо поддерживать не более
мм) погрешность расфокусировки необходимо поддерживать не более ![]() 0,05 мм.
0,05 мм.
ФПМ видеоусилителя определяется следующей формулой:
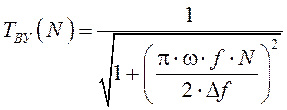
где ![]() полоса пропускания видеоусилителя
полоса пропускания видеоусилителя
На рисунке 10 представлены ФПМ видеоуслителя ![]() и пороговая модуляционная характеристика
и пороговая модуляционная характеристика ![]() .
.

Рисунок 10 - ФПМ видеоусилителя и ПМХ
ФПМ сдвига изображения определяется следующей формулой
 ,
,
где ![]() время экспозиции,
время экспозиции, ![]() скорость скомпенсированного изображения. На рисунке 11 представлены ФПМ сдвига изображения
скорость скомпенсированного изображения. На рисунке 11 представлены ФПМ сдвига изображения ![]() и пороговая модуляционная характеристика
и пороговая модуляционная характеристика ![]() .
.
ФПМ элементарного приемника излучения (апертуры) и предварительного усилителя. Эта составляющая определяется геометрией приемника излучения и описывается Фурье-преобразованием пространственного распределения чувствительности отдельного приемника излучения, также характеризуется пропускной способность предварительного усилителя
 ,
,
где ![]() ,
, ![]() размер приемника излучения матрицы цифровой ИКС,
размер приемника излучения матрицы цифровой ИКС, ![]() полоса пропускания предварительного усилителя,
полоса пропускания предварительного усилителя, ![]() количество элементов фоточувствительной матрицы соответственно по строке и по столбцу,
количество элементов фоточувствительной матрицы соответственно по строке и по столбцу, ![]() частота кадров,
частота кадров, ![]() фокусное расстояние.
фокусное расстояние.

Рисунок 11 - ФПМ сдвига изображения и ПМХ
На рисунке 12 представлены ФПМ элементарного приемника излучения и предварительного усилителя ![]() и пороговая модуляционная характеристика
и пороговая модуляционная характеристика ![]() .
.
ФПМ видеоконтрольного устройства имеет вид
![]()
 ,
,
где ![]() - характеристическая частота экрана монитора.
- характеристическая частота экрана монитора.

Рисунок 12 - ФПМ элементарного приемника излучения и ПМХ
На рисунке 13 представлены ФПМ моделируемой, цифровой ИКС ![]() и пороговая модуляционная характеристика
и пороговая модуляционная характеристика ![]() , пространственная частота по оси абсцисс на которой происходит пересечение ФПМ ИКС и ПМХ соответствует разрешающей способности моделируемой ИКС.
, пространственная частота по оси абсцисс на которой происходит пересечение ФПМ ИКС и ПМХ соответствует разрешающей способности моделируемой ИКС.
|

Рисунок 13 - Аналитическое определения разрешающей способности моделируемой ИКС по ФПМ и ПМХ
На рисунках 14-17 показаны некоторые зависимости углового разрешения моделируемой ИКС от величин, влияющих на него параметров (учтенных в разработанной математической модели).

Рисунок 14 - Зависимость углового разрешения от величины фокусного расстояния для трех зафиксированных размеров ПИ

Рисунок 15 - Зависимость углового разрешения ИКС от величины расфокусировки для трех зафиксированных величин фокусных расстояний
Анализ представленного выше аналитического исследования показал, что значение углового разрешения достаточно чувствительно к изменению рассмотренных выше факторов (погрешность фокусировки, параметры атмосферы, диафрагменное число, вибрации аэрофотоустановки, параметры полета и др.).
В разработанной математической модели учтены все существенные факторы, оказывающие влияния на величину углового разрешения ИКС ДЗЗ.

Рисунок 16 - Зависимость углового разрешения от размера элементарного ПИ для двух диапазонов длин волн

Рисунок 17 - Зависимость углового разрешения от размера элементарного ПИ для двух зафиксированных экспозиций
Заключение
Проведенное исследование разработанной математической модели цифровой ИКС «смотрящего» типа подтвердило её адекватность на изменение условий применения (влияние дымки, турбулентности атмосферы, вибраций фотоустановки, скорости носителя цифровой ИКС) и изменение конструктивный параметров конкретной ИКС (объектива, системы фокусировки, видеоусилителя, приемника излучения). Модель позволяет определить, лежит ли угловое разрешение цифровой ИКС в пределах допуска для конкретных условий применения.
С учетом того, что угловое разрешение является важнейшим параметром для оценки эффективности применения ИКС ДЗЗ, очевидно, что разработанная математическая модель оценки углового разрешения позволяет не только сформировать эталонные параметры для углового разрешения (в рамках статистической оценки технического состояния ОЭС ДЗЗ), но и оценить эффективность конкретной цифровой ИКС в заданных условиях применения (параметры полета, параметры атмосферы).
Работа поддержана Российским фондом фундаментальных исследований. Проекты №11-08-00850, № 11-08-00292.
Литература
1 Мельканович А.Ф., Янутш Д.А. К вопросу о синтезе аэрофотографической системы // Журнал научной и прикладной фотографии и кинематографии. 1979.- т. 24, вып. 1.
2 Тарасов В.В., Якушенков Ю.Г. Инфракрасные системы «смотрящего» типа. – М.: Логос, 2004. - 444 c.
3 Красильников Н.Н. Теория передачи и восприятия изображения. - М.: Радио и связь, 1986. – 246 c.
4 Регламент технического обслуживания самолета 6МР (часть 6 комплекс М100) / Ответственный за выпуск Тафинцев В.И. 1996. вып. № 6985.
5 Марр Д. Зрение. Информационный подход к изучению представления и обработки зрительных образов. – М.: Радио и связь, 1987.- 400 c.
6 Коваленко В.П. Оптико-электронное разведывательное оборудование летательных аппаратов. – М.: ВВИА им. проф. Н.Е. Жуковского, 1990.
7 Белоглазов И.Н., Шпилевой Ю.М. Вывод пороговой модуляционной характеристики иконических оптико-электронных средств на основе теории оптимального обнаружения. Научно-методические материалы “Применение ЭВМ для автоматизации процессов сбора и обработки информации”.- М.: ВВИА им. проф. Н.Е. Жуковского, 1984.
8 Веселов Ю.Г., Карпиков И.В. Особенности оценки характеристик шума цифровых оптико-электронных систем инфракрасного диапазона по изображениям, полученным в лабораторных условиях // Труды ВВА имени профессора Н.Е. Жуковского и Ю.А. Гагарина. Авиационное оборудование / Под ред. С.П. Халютина. – М.: ВВА имени профессора Н.Е. Жуковского и Ю.А. Гагарина, 2009.
9 Справочник по инфракрасной технике:в 4 т. / под ред. У. Вольфа, Г. Цисиса. – М.: Мир, 1999.
10 Мирошников М.М. Теоретические основы оптико–электронных приборов. – Л.: Машиностроение, 1977.- 600 c.
11 Веселов Ю.Г., Пономаренко А.В., Тихонычев В.В., Халтобин В.М. Исследование характеристик цифровых фотоаппаратов // Техника кино и телевидения.- 2003.- №6.- С. 39-41.
Публикации с ключевыми словами: цифровые инфракрасные системы, угловое разрешение, функция передачи модуляции, пороговая модуляционная характеристика
Публикации со словами: цифровые инфракрасные системы, угловое разрешение, функция передачи модуляции, пороговая модуляционная характеристика
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



