научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0410536
УДК 681.06
Россия, МГТУ им. Н.Э. Баумана
Введение
Метод на основе обобщенного полиномиального хаоса (ОПХ) [1-3], обеспечивает анализ и синтез динамической системы при наличии неопределенности (начальные условия, параметры, структура и воздействия окружающей среды). Полученное решение использует средние значения параметров системы с вероятностной неопределенностью. Предполагается, что функция плотности вероятности значений этих параметров известна.
При решении задачи синтеза и анализа стохастических динамических систем на основе ОПХ скорость сходимости и точность решения зависят от числа членов разложения. Метод ОПХ имеет преимущество перед классическими методами (метод Монте-Карло, ![]() и другие).
и другие).
1 Постановка задачи
Рассмотрим задачу синтеза оптимального управления в стохастических линейных системах [3-5]. Модель системы имеет вид
![]()
где ![]() ;
;
![]()
![]() - матрицы с параметрической неопределенностью;
- матрицы с параметрической неопределенностью; ![]() - вектор состояния системы;
- вектор состояния системы; ![]() - вектор управления;
- вектор управления; ![]() - вектор случайных процессов (СП).
- вектор случайных процессов (СП).
Ставится задачу синтеза управления стохастической динамической системой: найти закон управления с обратной связью в виде
![]() (2)
(2)
чтобы минимизировать целевой функционал
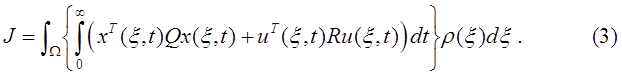
2 Решение задачи
Для решения задачи используется расширение полиномиального хаоса Винера-Аски [2,3], являющееся обобщением расширения оригинального винеровского хаоса, но с использованием полного ОПХ. Каждый компонент состояния системы ![]() будет множеством ортогональных СП, представленных в виде
будет множеством ортогональных СП, представленных в виде
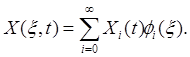 (4)
(4)
Каждая функция базиса ![]() ОПХ формирует ортогональный базис и означает среднее
ОПХ формирует ортогональный базис и означает среднее
![]() (5)
(5)
где ![]() - функция Кронекера, оператор
- функция Кронекера, оператор ![]() - среднее взвешенное произведение.
- среднее взвешенное произведение.
Для СП среднее взвешенное произведение ![]() на гильбертовом пространстве определяется выражением
на гильбертовом пространстве определяется выражением
![]() (6)
(6)
где ![]() - весовая функция - функция плотности вероятности СП
- весовая функция - функция плотности вероятности СП ![]() , связанная с отдельной выборкой из ОПХ Винера-Аски,
, связанная с отдельной выборкой из ОПХ Винера-Аски, ![]() - оператор математического ожидания, взятый по отношению к функции плотности вероятности соответствующего полиномиального базиса. Тогда среднее произведение ортогонального полинома базисных функций равно
- оператор математического ожидания, взятый по отношению к функции плотности вероятности соответствующего полиномиального базиса. Тогда среднее произведение ортогонального полинома базисных функций равно
![]()
Выборка базисных функций по схеме Винера-Аски зависит от распределения вероятности.
Каждый тип полинома из схемы Винера-Аски формирует комплексный базис в гильбертовом пространстве. В таблице 1 показаны некоторые общие распределения вероятностей и их связь с полиномиальным базисом в схеме Винера-Аски.
С помощью ОПХ [1-3] процессы ![]() ,
, ![]() и матрицы
и матрицы ![]() ,
, ![]() можно переписать в виде
можно переписать в виде

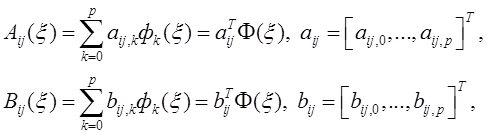 (7)
(7)
где![]() - базисные функции, зависящие от вида СП
- базисные функции, зависящие от вида СП ![]() (табл. 1); коэффициенты
(табл. 1); коэффициенты ![]() и
и ![]() получены методом проекцией Галеркина [3, 4] на
получены методом проекцией Галеркина [3, 4] на ![]() :
:
 ,
,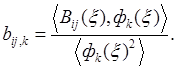 (8)
(8)
Обозначим

Закон управления в форме обратной связи зависит от плотнсти вероятности СП и состояния системы (2) вида [1, 5]:
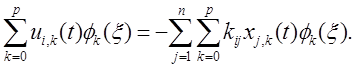 (9)
(9)
Закон управления является стохастическим из-за стохастической траектории состояния и входит в целевую функцию ![]() . Минимум целевой функций достигается с помощью оптимального управления
. Минимум целевой функций достигается с помощью оптимального управления
![]() (10)
(10)
где ![]() - произведение Кронекера.
- произведение Кронекера.
Если управление оптимально, то целевой функционал принимает минимальное значение. Матрица К должна удовлетворять решению уравнения Риккати
![]()
В результате выбора структуры управления с обратной связью по состоянию получаем модель системы вида
![]() (11)
(11)
Таким образом, мы преобразуем модель вида (1) с неопределенными параметрами в модель (11) с расширенной размерностью.
Таблица 1.
Связь ОПХ и типов случайного процесса ![]()
Случайный процесс | ОПХ |
Гауссова Равномерная гамма бета пуассона | Эрмит Лежандр Лагерр Якоби Шарлье |
3 Пример
Применим метод ОПХ для решения задачи синтеза оптимального управления стохастической системой вида
 (12)
(12)
где ![]() – СП с однородным распределением в области
– СП с однородным распределением в области ![]() . Базисными функциями являются полиномы Лежандра (см. табл. 1).
. Базисными функциями являются полиномы Лежандра (см. табл. 1).
Для этого примера возьмем порядок полинома Лежандра p=4:
![]()
![]()
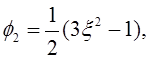
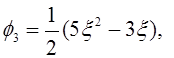
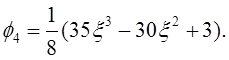
Выполним ОПХ разложение ![]() . Система (12) после ОПХ разложения приобретает вид
. Система (12) после ОПХ разложения приобретает вид
 (13)
(13)
где ![]()
![]() .
.
Приведем численный пример. Для системы (12) заданы начальные условия ![]() .
.
На рис. 1, 2 показаны результаты моделирования с помощью метода ОПХ и методом Монте-Карло. Красные линии - результаты, полученные методом ОПХ, зеленые - результаты, полученные методом Монте-Карло.
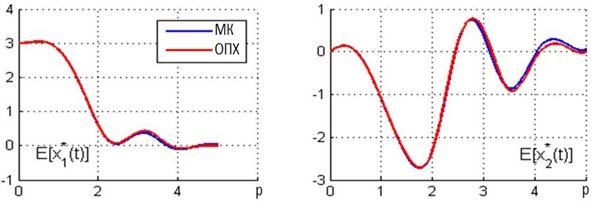
Рисунок 1 - Средние значения траектории состояния системы
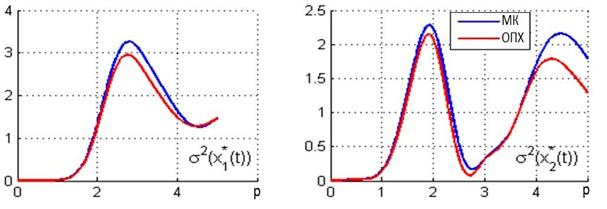
Рисунок 2 – Оценки дисперсии траектории состояния системы
Результаты показывают, что оценки средних значений и оценки дисперсий, полученные ОПХ и метод Монте-Карло достаточно близки.
Заключение
Предложен метод разложения ОПХ позволяет анализировать линейные и нелинейные стохастические дифференциальные уравнения как детерминированные. Другие основные результаты представленного метода включают в себя возможность решить задачи оптимального стохастического управления в виде детерминированной задачи.
Данный метод можно применять в задаче синтеза систем оптимального управления, а также в задаче идентификации нелинейных стохастических динамических объектов.
Литература
1. Beckmann P., Orthogonal Polynomials for Engineers and Physicists / P. Beckmann. - Golem Press, 1973, 280p.
2. Datta K.B., Orthogonal Functions in Systems and Control / K.B Datta, . - World Scientific Press, 1995, 288p.
3. Polyak B.T., Probabilistic robust design with linear quadratic regulators / B.T. Polyak and R. Tempo, - Systems and Control, 2001, V. 43, p. 343-353,.
4. Sun J., Stochastic Dynamics and Control / J. Sun - Science Press, 2006, 417p.
5. Пупков К.А. Методы робастного и адаптивного управления / К.А.Пупков-М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.-744с.
Публикации с ключевыми словами: обобщенный полиноминальный хаос, анализ и синтез системы управления, стохастический динамический объект
Публикации со словами: обобщенный полиноминальный хаос, анализ и синтез системы управления, стохастический динамический объект
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



