научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0405070
УДК 629.3.027.74
Россия, Алтайский государственный технический университет им. И.И. Ползунова
В конструкциях современных гусеничных машин для снижения динамических нагрузок и повышения ресурса гусеничного движителя применяют силовые резиновые и резинометаллические элементы. Наибольшее распространение получила конструкция гусеничного движителя с резинометаллическими шарнирами (РМШ) с силовыми резиновыми элементами и с ограничителем радиальной деформации, обеспечивающих соединение траков гусеничной цепи. В таком шарнире угловое перемещение траков относительно друг друга, обеспечивается за счет деформирования резиновых элементов, а растягивающее усилие передается как резиновыми элементами, так и ограничителями. Применение РМШ позволяет повысить податливость гусеничной цепи, и тем самым значительно снизить динамические нагрузки, действующие на элементы не только гусеничного движителя, но и на элементы трансмиссии, исключить попадание абразива на поверхности трения, снизить потери мощности [1, 2].
Ресурс резинометаллического шарнирного соединения зависит от долговечности резиновых элементов, от усталостной прочности и жесткости металлической арматуры пальца, от износа в области контакта ограничитель-проушина.
Резинометаллическое шарнирное соединение гусеничного движителя испытывает начальные деформации, вызванные запрессовкой пальца шарнира в проушины смежных звеньев и последующее (вторичное) нагружение во время эксплуатации:
- деформации, вызванные поворотом звеньев относительно друг друга;
- нагружение, вызванное растягивающим усилием в цепи;
- деформации осевого сдвига, вызванные смещением траков параллельно оси шарнира.
Кроме того, все указанные виды нагрузок могут действовать одновременно.
Для определения напряженно-деформированного состояния при вторичном нагружении необходимо предварительно определить деформации и напряжения, действующие в резинометаллическом пальце шарнира, вызванные его запрессовкой в проушины смежных звеньев.
В настоящей работе предложен алгоритм расчета напряженно-деформированного состояния резинометаллического пальца, вызванного запрессовкой в проушины смежных звеньев гусеничной цепи и при последующем деформировании, вызванном относительным поворотом звеньев.
Поскольку конструкция пальца резинометаллического шарнира, как видно на рис. 1, состоит из металлической арматуры и привулканизированных к ней резиновых элементов, то предлагаемый метод расчета должен описывать механическое поведение при совместном деформировании резины и металла.
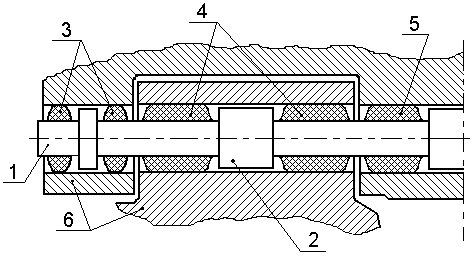
Рис. 1. Резинометаллическое шарнирное соединение траков гусеничной цепи:
1 – металлическая арматура пальца; 2 – ограничитель радиальной деформации; 3 – резиновые элементы крайней тройной проушины; 4 – резиновые элементы двойных проушин; 5 – резиновые элементы центральной проушины; 6 – смежные звенья.
При сборке резина испытывает большие деформации, поэтому алгоритм расчета резиновых элементов базируется на основных соотношениях нелинейной теории упругости несжимаемого материала. Алгоритм позволяет, используя пошаговую процедуру и линеаризированные соотношения теории наложения малых деформаций на конечные деформации, оценивать напряженное состояние, как при конечных деформациях, так и при вторичном нагружении. Механическое поведение резины описывается упругим потенциалом Трелоара [3-5].
Поведение металлической части шарнира (арматуры) описывается соотношениями линейной теории упругости в цилиндрической системе координат.
Поскольку для определения деформированного состояния резиновых элементов используется пошаговая процедура, то и для определения деформирования металлической арматуры пальца функционал приращения потенциальной энергии на каждом шаге деформирования арматуры должен учитывать деформации, полученные на предыдущем шаге. Учитывая вышесказанное, функционал приращения потенциальной энергии запишется в виде
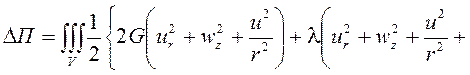

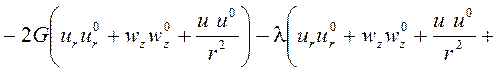
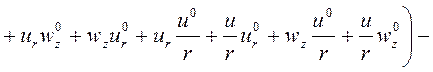
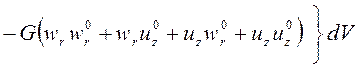 , (1)
, (1)
где
 - модуль сдвига;
- модуль сдвига;
![]() - модуль упругости;
- модуль упругости;
![]() - коэффициент Пуассона;
- коэффициент Пуассона;
 - постоянная Ляме;
- постоянная Ляме;
![]() ,
, ![]() - приращение перемещений в радиальном и осевом направлении на рассматриваемом шаге деформирования;
- приращение перемещений в радиальном и осевом направлении на рассматриваемом шаге деформирования;
![]() ,
, ![]() - суммарные перемещения в радиальном и осевом направлении, полученные на предыдущих шагах.
- суммарные перемещения в радиальном и осевом направлении, полученные на предыдущих шагах.
Здесь и далее нижние индексы обозначают частные производные по соответствующим координатам.
Для численной реализации алгоритма используется метод конечных элементов. Описание геометрической формы рассматриваемой конструкции и аппроксимация перемещений осуществлена четырехугольными изопараметрическими элементами с нелинейной аппроксимацией перемещений.
Функции формы для конечного элемента записываются в терминах безразмерных координат ![]() ,
,![]() в виде [6,7]
в виде [6,7] ![]()
Координаты и перемещения точки элемента соответственно определяются выражениями [6]:
![]() ;
; ![]() ;
;
![]() ;
; ![]() , (2)
, (2)
где
![]() ,
, ![]() - векторы соответствующих координат узловых точек конечного элемента;
- векторы соответствующих координат узловых точек конечного элемента;
![]() ,
, ![]() - векторы соответствующих перемещений узловых точек конечного элемента.
- векторы соответствующих перемещений узловых точек конечного элемента.
С учетом выражений (2) в матричном виде функционал (1) запишется
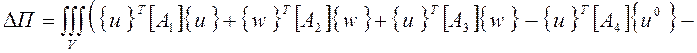
![]() , (3)
, (3)
где

 ;
;
 ;
;
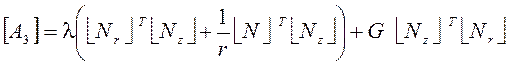 ;
;
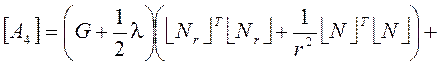
 ;
;
 ;
;
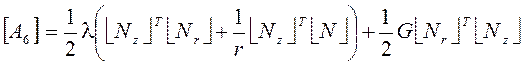 ;
;
![]() ,
, ![]() ,
,![]() - соответственно функция формы конечного элемента и ее производные по координатам [5].
- соответственно функция формы конечного элемента и ее производные по координатам [5].
Для минимизации функционала дифференцируем выражение (3) и получаем

 (4)
(4)
В соответствии с выражением (4) матрица жесткости элемента, описывающего упругое поведение металла, запишется в виде
 , (5)
, (5)
где ![]() - якобиан преобразования координат.
- якобиан преобразования координат.
Произведение  , где
, где
 , (6)
, (6)
позволяет учесть влияние деформации элемента определенной на предыдущих шагах деформирования. Матрица жесткости конечного элемента описывающего поведение резины при сборке вычисляется, как это показано в работе [5].
Приведенные соотношения позволяют последовательно определить распределение перемещений, компонентов тензора деформации и напряжений, а также их инвариантов в теле резинометаллического пальца шарнира после сборки.
Рассмотрим алгоритм расчета напряженно-деформированного состояния при вторичном нагружении вызванном поворотом звеньев. Функционал приращения потенциальной энергии металлической арматуры при кручении записывается в виде
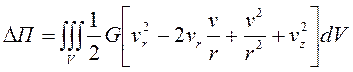 , (7)
, (7)
где ![]() - перемещения в окружном направлении.
- перемещения в окружном направлении.
В матричном виде выражение (7) перепишется в следующем виде
 , (8)
, (8)
где 
Для минимизации функционала дифференцируем выражение (8) и получаем
 (9)
(9)
Матрица жесткости, описывающая упругое поведение металлического конечного элемента при вторичном нагружении крутящим моментом запишется в виде
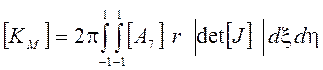 (10)
(10)
Матрица жесткости (10) вычисляется по координатам в деформированном сборкой состоянии. Матрица жесткости конечного элемента описывающего поведение резины при кручении вычисляется, как это показано в работе [5].
Изложенные выше соотношения положены в основу программного комплекса. Программный комплекс позволяет по заданным конструктивным параметрам шарнирного соединения автоматически получать конечно-элементную модель резинометаллического пальца и учитывать граничные условия. Полученные в результате расчета поля перемещений, тензоров деформаций и напряжений и их инвариантов выводятся в графическом виде.
На рис. 2 – 5 представлены картины распределения напряжений вызванных сборкой и последующим кручением (рис. 6, 7), полученные для конструкции РМШ гусеничной цепи трактора 4-го тягового класса.
Проанализируем полученные картины распределения напряжений, при этом особое внимание уделим области присоединения резиновых элементов к металлической арматуре пальца.
Центральная часть области соединения резины и металла испытывает напряжения сжатия ![]() (рис. 2). Максимальные значения напряжений составляют: для резиновых элементов крайней проушины (область I) – 1,89 МПа; для резиновых элементов двойных проушин (область II) – 3,23 МПа; для резиновых элементов центральной проушины (область III) – 2,99 МПа. Напряжения
(рис. 2). Максимальные значения напряжений составляют: для резиновых элементов крайней проушины (область I) – 1,89 МПа; для резиновых элементов двойных проушин (область II) – 3,23 МПа; для резиновых элементов центральной проушины (область III) – 2,99 МПа. Напряжения ![]() уменьшаются от указанных областей к периферии резинного элемента в области соединения и в направлении уменьшения радиуса пальца и возрастают в направлении увеличения радиуса в центральной части резинового элемента.
уменьшаются от указанных областей к периферии резинного элемента в области соединения и в направлении уменьшения радиуса пальца и возрастают в направлении увеличения радиуса в центральной части резинового элемента.

Рис. 2. Распределение напряжений ![]() (сборка)
(сборка)
Аналогичная картина распределения напряжений получена для напряжений ![]() (рис. 3). В области соединения резины и металла максимальных значений напряжения сжатия
(рис. 3). В области соединения резины и металла максимальных значений напряжения сжатия ![]() достигают в центральной части соединения и составляют для резиновых элементов проушин: крайней тройной (область I) – 1,89 МПа; для двойных (область II) – 2,69 МПа; для центральной (область III) - 2,49 МПа.
достигают в центральной части соединения и составляют для резиновых элементов проушин: крайней тройной (область I) – 1,89 МПа; для двойных (область II) – 2,69 МПа; для центральной (область III) - 2,49 МПа.

Рис. 3. Распределение напряжений ![]() (сборка)
(сборка)
Особенностью распределения напряжений ![]() (рис. 4) является то, что в центральной части соединения резиновых элементов и металла резиновые элементы испытывают напряжения сжатия, а металлическая арматура напряжения растяжения. Значение напряжений сжатия для резиновых элементов составляют: в области I – 1,43 МПа; в области II – 3,01 МПа; в области III – 2,69 МПа. Значение напряжений растяжения для металла в соединении с резиновыми элементами составляют: в области I – 1,73 МПа; в области II и III – 2,68 МПа.
(рис. 4) является то, что в центральной части соединения резиновых элементов и металла резиновые элементы испытывают напряжения сжатия, а металлическая арматура напряжения растяжения. Значение напряжений сжатия для резиновых элементов составляют: в области I – 1,43 МПа; в области II – 3,01 МПа; в области III – 2,69 МПа. Значение напряжений растяжения для металла в соединении с резиновыми элементами составляют: в области I – 1,73 МПа; в области II и III – 2,68 МПа.
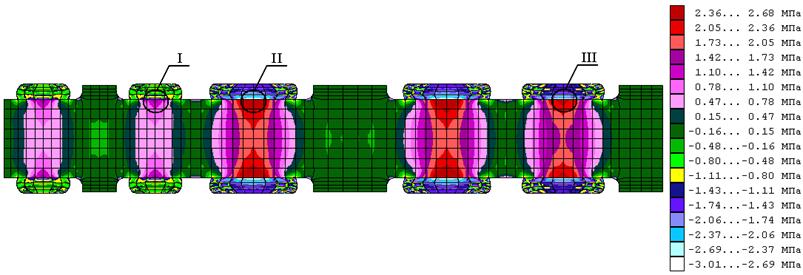
Рис. 4. Распределение напряжений ![]() (сборка)
(сборка)
Касательные напряжения ![]() (рис. 5) вызванные сборкой, достигают максимальных значений в области соединения резины и металла на расстоянии 2,5…3,0 мм (область I) от крайней точки соединения для элементов крайней тройной проушины и на расстоянии 4,5…5,5 мм (области II и III) для элементов двойных и центральной проушины, и составляют: в области I – 1,00 МПа; в областях II и III – 1,49 МПа. Необходимо отметить, что именно в этих областях наблюдается разрушение резиновых элементов при сборке.
(рис. 5) вызванные сборкой, достигают максимальных значений в области соединения резины и металла на расстоянии 2,5…3,0 мм (область I) от крайней точки соединения для элементов крайней тройной проушины и на расстоянии 4,5…5,5 мм (области II и III) для элементов двойных и центральной проушины, и составляют: в области I – 1,00 МПа; в областях II и III – 1,49 МПа. Необходимо отметить, что именно в этих областях наблюдается разрушение резиновых элементов при сборке.

Рис. 5. Распределение напряжений ![]() (сборка)
(сборка)
Касательные напряжения ![]() (рис. 6) вызванные закручиванием шарнира, достигают максимальных значений в центральной части соединения резины и металла. Для резиновых элементов тройных проушин (область I и III) максимальные значения касательных напряжений
(рис. 6) вызванные закручиванием шарнира, достигают максимальных значений в центральной части соединения резины и металла. Для резиновых элементов тройных проушин (область I и III) максимальные значения касательных напряжений ![]() достигают 0,46 МПа, а для двойных (область II) – 0,47 МПа. Наблюдается также некоторая концентрация касательных напряжений в области радиуса перехода от диаметра основного пальца к диаметру ограничителя (область IV).
достигают 0,46 МПа, а для двойных (область II) – 0,47 МПа. Наблюдается также некоторая концентрация касательных напряжений в области радиуса перехода от диаметра основного пальца к диаметру ограничителя (область IV).

Рис. 6. Распределение напряжений ![]() (кручение)
(кручение)
Касательные напряжения ![]() (рис. 7) вызванные закручиванием шарнира, достигают максимальных значений в области перехода от центральной проушины к двойной (область II) и от двойной проушины к крайней (область I). Максимальные значения касательных напряжений
(рис. 7) вызванные закручиванием шарнира, достигают максимальных значений в области перехода от центральной проушины к двойной (область II) и от двойной проушины к крайней (область I). Максимальные значения касательных напряжений ![]() достигают в области I – 3,16 МПа и в области II – 2,63 МПа. Внешние слои арматуры пальца более нагружены.
достигают в области I – 3,16 МПа и в области II – 2,63 МПа. Внешние слои арматуры пальца более нагружены.

Рис. 7. Распределение напряжений ![]() (кручение)
(кручение)
Таким образом, предложенный алгоритм позволяет определить напряженно-деформированное состояние резинометаллического пальца шарнирного соединения, вызванное сборкой шарнира и при последующем деформировании при закручивании. На основе анализа распределения перемещений, деформаций, напряжений их инвариантов оценить рациональность выбора конструктивных параметров существующих конструкций и обоснованно их выбрать для вновь проектируемых вариантов РМШ.
Кроме того, представленный алгоритм является необходимым этапом, позволяющим получить информацию для расчета последующего нагружения от растягивающего усилия в цепи.
Следующим этапом работы будет разработка алгоритма расчета напряженно-деформированного состояния резинометаллического пальца при действии растягивающего усилия в гусеничной цепи.
СПИСОК ЛИТЕРАТУРЫ
1. Барсуков Ю.Н. Экспериментальное исследование динамической нагруженности трансмиссии трактора класса 3 тс /Ю.Н. Барсуков, Л.Н. Беседин, В.Ф. Комаров //Труды АПИ. Вып. 54. - Барнаул, 1975. - С. 69 – 75.
2. Дружинин В.А. К вопросу об использовании гусениц с резинометаллическими шарнирами/В.А. Дружинин, В.А. Целищев // Совершенствование систем автомобилей, тракторов и агрегатов: сб. статей / под ред. к.т.н., профессора В.А. Дружинина / Академия транспорта РФ, АлтГТУ им. И.И. Ползунова.- Барнаул, 1999. – С. 11-18.
3. Лавендел Э.Э. Расчеты резинотехнических изделий.: Монография – М.: Машиностроение, 1976. – 232 с.
4. Дымников С.И. Расчет напряженно-деформированного состояния запрессованных резиновых элементов комбинированного шарнира методом последовательных приближений/С.И. Дымников, В.А. Дружинин //Каучук и резина. – 1977.-№6. – С. 47 – 51.
5. Коростелев С.А. Оценка напряженно-деформированного состояния резинового элемента РМШ гусеничного движителя при сборке и кручении/ С.А. Коростелев //Тракторы и сельхозмашины. – 2010.- № 11. – С. 26 – 29.
6. Галлагер Р. Метод конечных элементов. Основы.: Монография – М.: Мир, 1984. 428 с.
7. Сегерлинд Л. Применение метода конечных элементов.: Монография – М.: Мир, 1979. 392 с.
Публикации с ключевыми словами: напряженно-деформированное состояние, гусеничный движитель, резинометаллический шарнир, резинометаллический палец
Публикации со словами: напряженно-деформированное состояние, гусеничный движитель, резинометаллический шарнир, резинометаллический палец
Смотри также:
- Исследование влияния толщины и угла раскрытия рабочей лопатки центростремительной турбины на поле напряжений, возникающих в ней
- 77-30569/286502 Расчетно-экспериментальное обоснование прочности и надежности шатунов при создании и модернизации высокофорсированных двигателей.
- Конечно-элементная модель анализа напряженно-деформированного состояния деталей, образующих газовый стык среднеоборотного дизеля, от монтажных нагрузок
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



