научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК.621
МГТУ им. Н.Э. Баумана
Введение
Релаксация силы в сжатой пружине – это негативный фактор при эксплуатации тепловыделяющей сборки энергетического реактора, который обусловлен развитием в материале пружины необратимых деформаций ползучести под действием высокой температуры и флакса нейтронов. Релаксационная стойкость пружины – это способность материала, из которого изготовлена пружина, сопротивляться возникновению необратимых деформаций ползучести и падению напряжений в нем. Релаксационная стойкость пружины оценивается, в основном, по скорости падения силы в сжатой пружине, которую принято представлять кривыми релаксации. Основная цель разработанной математической модели – это возможность построения кривых релаксации для пружины, с различными геометрическими параметрами и работающей в различных условиях температурного и нейтронного воздействий. При этом существенным является разработка эффективного алгоритма и программы расчета, удобных в инженерной практике.
Основные соотношения математической модели
Состоянию чистой релаксации соответствует постоянства во времени деформированного состояния. Такое состояние реализуется при фиксированной высоте предварительно сжатой пружины. При этом напряженное состояние во времени изменяется и сила сжатия пружины падает. На рис. 1 представлена схема реализации условий чистой релаксации. Основные геометрические параметры деформированной пружины ясны из рисунка и остаются неизменными во времени.
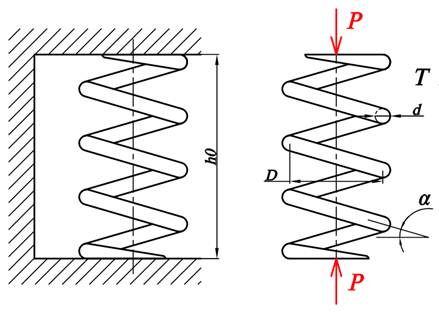
Рис. 1. Схемы закрепления и нагружения пружины
В поперечном сечении витка пружины возникают внутренние силовые факторы, представленные на рис. 2. Из условий равновесия отсеченной части пружины следуют известные соотношения теории пружин [ 1 ].
 (1)
(1)
где ![]() - крутящий момент,
- крутящий момент, ![]() - изгибающий момент,
- изгибающий момент, ![]() - поперечная сила,
- поперечная сила, ![]() - нормальная сила. Здесь также учтен крутящий момент mна торцах пружины, возникающий при запрете их поворота. Моменты Mzи My, в свою очередь вызваны, изменением кручения и кривизны оси витка пружины
- нормальная сила. Здесь также учтен крутящий момент mна торцах пружины, возникающий при запрете их поворота. Моменты Mzи My, в свою очередь вызваны, изменением кручения и кривизны оси витка пружины ![]() и
и ![]() соответственно.
соответственно.
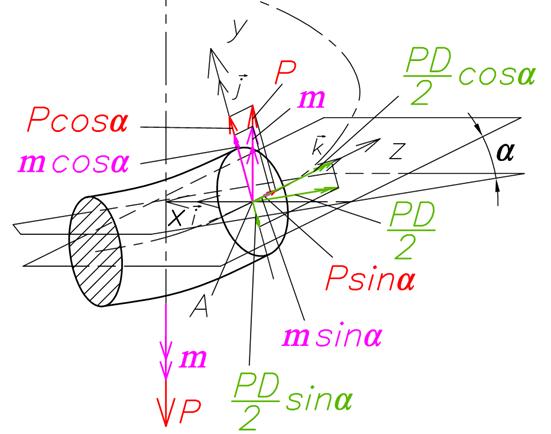
Рис. 2. Определение внутренних силовых факторов в пружине
Из курса дифференциальной геометрии известно, что кручение и кривизна винтовой линии пружины связаны с ее геометрическими параметрами соотношениями
 . (2)
. (2)
В начальный момент времени пружина находится в упругом состоянии, для которого при условии малой кривизны витка пружины справедливы соотношения
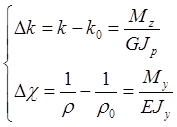 (3)
(3)
где ![]() и
и ![]() – полярный и осевой моменты инерции сечения витка пружины;
– полярный и осевой моменты инерции сечения витка пружины;
![]() и
и ![]() – измененный и начальный радиусы кривизны винтовой линии пружины.
– измененный и начальный радиусы кривизны винтовой линии пружины.
В этом случае однозначная связь между силой поджатия пружины и изменением ее геометрических параметров будет определяться следующим соотношением
 (4)
(4)
где ![]() и
и ![]() – угол подъема наклона витка и средний диаметр пружины соответствуют недеформированному состоянию, а
– угол подъема наклона витка и средний диаметр пружины соответствуют недеформированному состоянию, а ![]() и
и ![]() – соответствуют деформированному состоянию.
– соответствуют деформированному состоянию.
Напряженное состояние пружины определяется напряжениями: касательными – ![]() и
и ![]() и нормальным –
и нормальным – ![]() .
.
Компоненты напряжения ![]() и
и ![]() связаны с полным касательным напряжением
связаны с полным касательным напряжением ![]() соотношениями
соотношениями
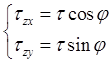 , (5)
, (5)
где угол ![]() отвечает полярной системе координат, связанной с сечением.
отвечает полярной системе координат, связанной с сечением.
Интенсивность напряжений для случая совместного кручения и изгиба имеет вид
![]() (6)
(6)
Под действием температуры и потока нейтронов в материале пружины развиваются процессы ползучести и как следствие изменяется во времени напряженное состояние. Уравнение состояния ползучести стали с учетом нейтронного облучения имеет вид [2]
 (7)
(7)
где ![]() ,
, ![]() ,
, ![]() - экспериментальные коэффициенты, зависящие от температуры;
- экспериментальные коэффициенты, зависящие от температуры;
![]() - флакс нейтронов или поток нейтронов,
- флакс нейтронов или поток нейтронов, 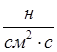 ,
,
![]() - универсальная газовая постоянная,
- универсальная газовая постоянная, 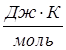 ,
,
![]() - температура активной зоны энергетического реактора,
- температура активной зоны энергетического реактора, ![]() ,
,
![]() - энергия активации ползучести,
- энергия активации ползучести, ![]() .
.
Скорости линейной и угловой деформаций ползучести определяются соотношениями теории ползучести [3]
 (8)
(8)
Условиями релаксации являются равенства скоростей кручения и кривизны винтовой оси пружины нулю.
Алгоритм численного расчета релаксации силы сжатия пружины
Напряженное состояние витка пружины неоднородно по его сечению. Для интегрирования напряжений разбиваем сечение на малые области. На рис. 3 представлен пример дискретизации сечения.

Рис. 3. Разбиение сечения витка пружины
Для определения изменения напряжений в пружине вводится соотношение между деформациями:
![]() , (9)
, (9)
где ![]() – деформация ползучести, соответствующая номерам
– деформация ползучести, соответствующая номерам ![]() области сечения;
области сечения;
![]() – упругая деформация, соответствующая номерам
– упругая деформация, соответствующая номерам ![]() области сечения;
области сечения;
![]() – начальная деформация, неизменяемая во времени.
– начальная деформация, неизменяемая во времени.
Записывая соотношение (9) в дифференциальной форме и используя конечно-разностное представление по времени получаем следующие зависимости релаксации
 , (10)
, (10)
где ![]() – текущий шаг по времени.
– текущий шаг по времени.
Выражения (10) связывают напряжения на следующем шаге и напряжения на предыдущем шаге. Скорости линейной и сдвиговой деформаций ползучести ![]() и
и ![]() определяются по напряжениям на предыдущем шаге в соответствии с зависимостями (6), (7), (8). Начальные значения напряжение определяются по упругому состоянию пружины. Интегрируя текущие значения напряжений по сечению определяем величины внутренних силовых факторов, через которые находится текущее значение силы сжатия пружины. Накопление деформаций ползучести определяется соотношениями
определяются по напряжениям на предыдущем шаге в соответствии с зависимостями (6), (7), (8). Начальные значения напряжение определяются по упругому состоянию пружины. Интегрируя текущие значения напряжений по сечению определяем величины внутренних силовых факторов, через которые находится текущее значение силы сжатия пружины. Накопление деформаций ползучести определяется соотношениями
 , (11)
, (11)
где ![]() и
и ![]() – накопленные деформации ползучести на предыдущем шаге.
– накопленные деформации ползучести на предыдущем шаге.
Данные соотношения позволяют определить изменения начальных размеров пружины после ее разгрузки.
На основе приведенного алгоритма расчета разработана программа в среде Matlab, позволяющая получать кривые релаксации силы сжатия при различных геометрических параметрах пружины и различных температурных и нейтронных воздействиях.
Результаты расчетов релаксации силы сжатия пружины
Рассматривалась задача многоэтапного поджатия пружины. Первый этап: сжатие на 15 мм, выдержка в течение 4000 ч; второй этап: дополнительное сжатие на 1 мм, общая осадка ![]() мм, время выдержки 4000 ч; третий этап:
мм, время выдержки 4000 ч; третий этап: ![]() мм, 4000 ч; четвертый этап:
мм, 4000 ч; четвертый этап: ![]() мм, 6000 ч. Результаты расчета представлены на рис. 4 – нижняя кривая. По горизонтальной оси на графике отложено время, по вертикальной оси – сила сжатия пружины.
мм, 6000 ч. Результаты расчета представлены на рис. 4 – нижняя кривая. По горизонтальной оси на графике отложено время, по вертикальной оси – сила сжатия пружины.
Для проверки работы алгоритма и программы расчета был выполнен расчет этой же задачи с помощью конечно-элементного комплекса Ansys 12. На рис. 5 представлена конечно-элементная модель пружины. Условия закрепления и нагружения пружины задавались из требования тождественности начальных состояний обеих расчетных моделей. Результаты конечно-элементного расчета представлены на рис. 4 верхней кривой.
Сопоставляя результаты решения задачи по двум моделям, видно, что разработанная программа дает несколько завышенную релаксацию по сравнению с решением задачи в Ansys 12. Однако общий вид кривых одинаковый и можно утверждать, что алгоритм разработанной программы построен и реализован верно. Завышенное значение релаксации приводит к более безопасной оценке ресурса работы пружины.

Рис. 4. Сравнение результатов решения задачи

Рис. 5. Конечно-элементная модель пружины
Выводы
В настоящей статье изложен инженерный метод расчета релаксации силы в сжатой пружине под действием температуры и потока нейтронов. Разработанная программа в среде программирования Matlab проверялась расчетом пружины при одинаковых условиях в расчетном комплексе Ansys 12. Установлено, что алгоритм разработанной программы построен верно.
Основными достоинствами разработанной программы можно считать:
- скорость решения задачи в разработанной программе превосходит скорость решения задачи в расчетном комплексе Ansys 12;
- возможность варьировать геометрические параметры пружины, внешние условия работы пружины;
- возможность учета изменения физико-механических свойств материала пружины.
Библиографический список:
1. Андреева Л.Е. Упругие элементы приборов. -М.: Машиностроение, 1981.- 392 с.
2. Киселевский В.Н. Изменение механических свойств сталей и сплавов при радиационном облучении. - Киев, Наукова Думка, 1977. – 287 с.
3. Бойл Дж., Спенс Дж. Анализ напряжений в конструкциях при ползучести. – М.: Мир, 1986.- 360 с.
Публикации с ключевыми словами: ползучесть, релаксация, расчет пружин, нейтронный поток
Публикации со словами: ползучесть, релаксация, расчет пружин, нейтронный поток
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



