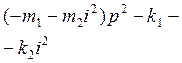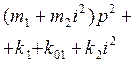научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК 62.752.
НИИ современных технологий, системного анализа и моделирования,
Иркутский государственный университет путей сообщения
Введение. Сочленения играют большую роль в динамике механических систем. Из разнообразие предопределяет интерес к связям, возникающим между элементами механизмов, кинематическим парам и соединениям [1, 2]. Понятие «сочленение» несколько отличается и от понятий «соединение», «кинематическая пара», «связь», поскольку несет на себе, в определенном смысле «предысторию» своего формирования. Под сочленением часто понимают некоторые особенности взаимодействия, возникающего между твердыми телами. В частности, сочленение может предсьавлять собой соединение двух твердых тел, обеспечивающего в некотром направлении, движение. При этом параметры звена соединения могут принимать предельные значения, например, в отношении увеличения жесткости соединения двух тел.
В простейших вариантах звенья, соединяемые шарниром, допускают вращательно-качательные движения относительно друг друга. При этом сочленение из общего числа степеней свободы производит «исключение» одной степени свободы в движениях. В практике виброзащиты могут встречаться звенья, замыкающие на себе через сочленения несколько элементов. Кроме соединения подвижных звеньев между собой часто встречаются соединения твердых тел с неподвижными звеньями или с основанием (или условно неподвижной системой).
Механические колебательные системы могут иметь сочленения различных типов, что обеспечивает особенности структуры системы и, так называемой, «метрики» [1]. Вращательные сочленения твердых тел привносят в системы рычажные связи. Поскольку сочленения уменьшают число степеней свободы системы в целом, то достаточно рациональным подходом представляется первоначальное составление общей модели без ограничений движения. В этом случае математическая модель системы может быть представлена в преобразованиях Лапласа в виде уравнения
![]() , (1)
, (1)
где ![]() - матрица операторных коэффициентов;
- матрица операторных коэффициентов;![]() - вектор-столбец переменных;
- вектор-столбец переменных;![]() - вектор столбец внешних воздействий.
- вектор столбец внешних воздействий.
В общем случае матрица A имеет порядок n×nи является симметричной. При построении математических моделей систем с сочленениями могут использоваться различные системы обобщенных координат, главным образом такие, в которых координаты отражают относительное движение. Сочленение может быть реализовано по отношению к элементу, совершающему «абсолютное» движение. Естественно, при этом, что системы координат допускают соответствующие взаимные преобразования.
Выбирая системы координат, соответствующим для поставленной задачи образом, отметим, что рассматриваемые пары или блоки сочленения будут находиться на диагонали матрицы. Введение сочленения означает исключение соответствующих столбцов и строк матрицы операторных коэффициентов, включая и «исключения» соответствующей правой части уравнения (1).
Внешнее воздействие в этом случае перераспределяется соответствующим образом при выборе систем обобщенных координат, где необходимо соблюдать условия равенства виртуальных работ обобщенных сил в различных системах обобщенных координат [3].
I. Общие положения. Постановка задач исследования. Рассматривается ряд конкретных примеров использования процедур, построения математических моделей, а также примеры сочленений. Набор возможных сочленений может обеспечивать сложные формы взаимодействий, в том числе и на основе кинематических пар IV и III, II классов [4]. На рис.1 представлена расчетная схема виброзащитной системы (ВЗС), в которой имеется два блока, наличие которых отражается контурами I и II. В основе блоков – твердое тело, обладающее массой и моментом инерции; в составе ВЗС задействованы упругие элементы, предполагается, что смещение центра тяжести блока I не оказывает существенного влияния на динамику системы в целом, а силы сопротивления достаточно малы.
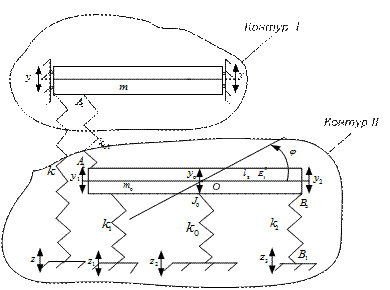
Рис. 1. Расчетная схема ВЗС, имеющей два контура взаимодействия
Расчетная схема в виде колебательной системы с тремя степенями свободы ![]() может рассматриваться как фрагмент ВЗС, в которой совместно работает блок I (контур I рис. 1) и блок II ( контур II рис. 1), состоящий из твердого тела, опирающегося на упругие опоры. Контуры I и II находятся во взаимодействии через упругий связующий элемент
может рассматриваться как фрагмент ВЗС, в которой совместно работает блок I (контур I рис. 1) и блок II ( контур II рис. 1), состоящий из твердого тела, опирающегося на упругие опоры. Контуры I и II находятся во взаимодействии через упругий связующий элемент ![]() . В свою очередь, твердое тело опирается не только на упругие опоры
. В свою очередь, твердое тело опирается не только на упругие опоры ![]() и
и ![]() , но имеет упругую связь
, но имеет упругую связь ![]() , линия действия которой проходит через центр тяжести балки в точке О. Примем, что
, линия действия которой проходит через центр тяжести балки в точке О. Примем, что ![]() ,
,![]() , а присоединенная масса
, а присоединенная масса ![]() не вызывает значительных изменений массоинерционных параметров системы. Силы сопротивления также полагаются малыми. Полагая жесткости
не вызывает значительных изменений массоинерционных параметров системы. Силы сопротивления также полагаются малыми. Полагая жесткости ![]() и
и ![]() достаточно большими, можно преобразовать расчетную схему к виду, как показано на рис. 2.
достаточно большими, можно преобразовать расчетную схему к виду, как показано на рис. 2.
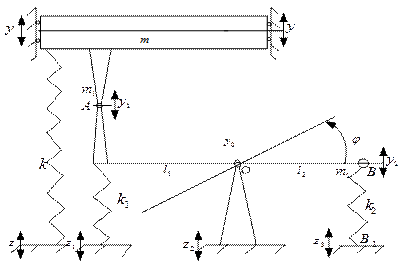
Рис. 2. Преобразованная расчетная схема, содержащая сочленения
Для полученной расчетной схемы могут быть получены математические модели, свойства которых зависят от выбора системы обобщенных координат. При этом представляет интерес формализм построения уравнений движения, на основе уоторых могут быть построены структурные схемы и определены передаточные функции системы. Последние дают возможность появления различных режимов движения и оценить роль и влияние введения сочленений.
II. Построение математических моделей. Запишем выражения для кинетической и потенциальной энергий для расчетной схемы ВЗС, приведенной на рис. 2.
 , (2)
, (2)
 , (3)
, (3)
где ![]() - скорость элемента массой
- скорость элемента массой ![]() в абсолютном движении, которая определяется из соотношения
в абсолютном движении, которая определяется из соотношения
 . (4)
. (4)
Знак минуc, отражает изменения движения, вызванное рычагами второго рода, таким образом найдем, что
 , (5)
, (5)
где  - передаточное отношение рычага.
- передаточное отношение рычага.
Потенциальная энергия определяется выражением
 (6)
(6)
Получим дифференциальное уравнение движения для системы рис. 2.
![]() , (7)
, (7)
Для упрощения расчетов примем, что ![]()
![]() и
и ![]()
тогда передаточная функция системы примет вид
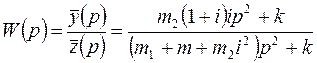 , (8)
, (8)
где ![]() - комплексная переменная (
- комплексная переменная (![]() ).
).
В качестве примера на рис.3 показано семейство амплитудно-частотных характеристик, построенных на основе (8) при изменении параметра передаточного отношения рычага i в пределах от 0÷3 с шагом 0,5. В качестве исходных приняты следующие параметры системы: ![]() кг;
кг; ![]() кг;
кг; ![]() Н/м
Н/м

Рис. 3. Семейство амплетудно-частотных характеристик системы
с передаточной функцией (8)
На рис. 3 через![]() обозначены частоты динамического гашения колебаний. Соответствующие значения частот собственных колебаний в сопоставлении с частотами динамического гашения приведены в табл.1.
обозначены частоты динамического гашения колебаний. Соответствующие значения частот собственных колебаний в сопоставлении с частотами динамического гашения приведены в табл.1.
Значения частот собственных колебаний в сопоставлении с частотами дигамического гашения ![]() для системы на рис.3
для системы на рис.3
Табл. 1
| 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
Значение частот динамического гашения |
|
|
|
|
|
|
25.81 | 15.81 | 11.54 | 9.12 | 7.55 | 6.45 | |
Значение частот собственных колебаний |
|
|
|
|
|
|
8.94 | 8.45 | 7.78 | 7.07 | 6.38 | 5.77 |
Из сравнения амплитудно-частотных характеристик следует, что при увеличении ![]() происходит смещение частот динамического гашения влево, то есть разность частот
происходит смещение частот динамического гашения влево, то есть разность частот ![]() уменьшается. При этом частота собственных колебаний также уменьшается, но гораздо медленнее. На высоких частотах коэффициент передачи амплитуды колебаний после режима динамического гашения стремится к предельному значению
уменьшается. При этом частота собственных колебаний также уменьшается, но гораздо медленнее. На высоких частотах коэффициент передачи амплитуды колебаний после режима динамического гашения стремится к предельному значению ; чем больше
; чем больше ![]() тем – больше будет значение
тем – больше будет значение ![]() . При
. При ![]() получим, что
получим, что  .
.
Более детализированная информация о свойствах динамического гасителя колебаний представлена в работе [5].
III. Построение математических моделей в различных системах координат.
Произведем ряд выкладок, в развитие метода получения математических моделей систем с сочленениями, основанного на упрощениях некоторых более общих систем. При этом используются особенности, возникающие при наложении связей. Вернемся к исходной схеме, приведенной на рис.1. Тогда выражения (5) и (6) для кинетической и потенциальной энергий можно преобразовать к виду
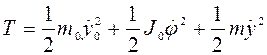 , (9)
, (9)
 , (10)
, (10)
где приняты (рис. 1) следующие обозначения: ![]() - момент инерции,
- момент инерции, ![]() - масса промежуточного тела (может превращаться в
- масса промежуточного тела (может превращаться в ![]() и
и ![]() , соединенных рычагом);
, соединенных рычагом); ![]() - масса объекта;
- масса объекта; ![]() ,
,![]() ,
, ![]() ,
, ![]() - упругие элементы, промежуточного тела, опирающегося на основание;
- упругие элементы, промежуточного тела, опирающегося на основание; ![]() - кинематические возмущения. Координаты точек
- кинематические возмущения. Координаты точек ![]() и
и ![]() , определяются следующим образом:
, определяются следующим образом:
![]() и
и ![]() . (11)
. (11)
Для получения сочленений между элементами необходимо выполнение условий
![]() ,
,![]() , (12)
, (12)
где исходные значения ![]() .
.
Определим для исследований координаты ![]() ,
, ![]() и запишем ряд соотношений
и запишем ряд соотношений
![]() ;
;![]() ,
,  ,
,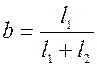 ,
, . (13)
. (13)
При движении объекта защиты в системе координат ![]() ,
, ![]() и
и ![]() выражение для кинетической энергии можно привести к виду:
выражение для кинетической энергии можно привести к виду:
 . (14)
. (14)
Соответственно для потенциальная энергия в данном случае определится
 . (15)
. (15)
В табл. 2 приведены значения коэффициентов уравнений в координатах, ![]() ,
, ![]() и
и ![]() , полученных обычным образом [2].
, полученных обычным образом [2].
Значения коэффициентов уравнений движения системы (рис.1)
в координатах ![]() ,
, ![]() и
и ![]()
Табл. 2
|
|
|
|
| 0 |
|
|
|
|
| 0 |
|
|
|
0 | 0 |
|
Обобщенные силы по координатам ![]() ,
, ![]() и
и ![]() имеют вид
имеют вид
![]() ;
;![]() ;
;![]() . (16)
. (16)
Полученные уравнения описывают движение в системе координат, отражающих вертикальные перемещения массоинерционных элементов ВЗС. Такую математическую модель можно назвать базовой. Особенность матрицы заключается в том, что ![]() =
=![]() =0,
=0, ![]() =
=![]() =0; это зависит от характера динамических взаимодействий, определяемых структурой ВЗС (рис.1) и выбором системы обобщенных координат.
=0; это зависит от характера динамических взаимодействий, определяемых структурой ВЗС (рис.1) и выбором системы обобщенных координат.
Перейдем к системе координат ![]() ,
, ![]() и
и ![]() ; запишем ряд соотношений
; запишем ряд соотношений ![]() и получим выражение для кинетической и потенциальной энергий
и получим выражение для кинетической и потенциальной энергий
 , (17)
, (17)
 . (18)
. (18)
Значения коэффициентов уравнений в координатах ![]() ,
, ![]() и
и ![]() соответственно представлены в табл.3.
соответственно представлены в табл.3.
Значения коэффициентов уравнений в координатах ![]() ,
, ![]() и
и ![]()
Табл. 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенные силы по координатам ![]() ,
, ![]() и
и ![]() имеют вид
имеют вид
![]() ;
;![]() ;
;![]() . (19)
. (19)
Математическая модель в системе координат ![]() ,
, ![]() и
и ![]() отличается от предыдущей модели (координаты
отличается от предыдущей модели (координаты ![]() ,
, ![]() и
и ![]() ) тем, что «нулевые» клетки в матрице коэффициентов отсутствуют. Что касается координаты
) тем, что «нулевые» клетки в матрице коэффициентов отсутствуют. Что касается координаты ![]() , то она может быть «обнулена» предположением, что
, то она может быть «обнулена» предположением, что ![]() и образуется сочленение, которое можно рассматривать как кинематическую пару. Физически это означает, что масса
и образуется сочленение, которое можно рассматривать как кинематическую пару. Физически это означает, что масса ![]() присоединяется к элементу ВЗС в т. А с массоинерционными параметрами
присоединяется к элементу ВЗС в т. А с массоинерционными параметрами ![]() ,
, ![]() и изменяет их (и общую массу и момент инерции). Движение системы будет описываться в этом случае координатами
и изменяет их (и общую массу и момент инерции). Движение системы будет описываться в этом случае координатами ![]() и
и ![]() . Необходимые данные для получения передаточных функций можно получить, исключая столбец и строку, содержащие
. Необходимые данные для получения передаточных функций можно получить, исключая столбец и строку, содержащие ![]() (фактически переменная устраняется, а порядок матрицы уменьшается на единицу).
(фактически переменная устраняется, а порядок матрицы уменьшается на единицу).
Для дальнейших расчетов введем систему координат ![]() ,
, ![]() и
и ![]() . Тогда выражения для кинетической и потенциальной энергий в координатах
. Тогда выражения для кинетической и потенциальной энергий в координатах ![]() ,
, ![]() и
и ![]() преобразуются к виду:
преобразуются к виду:
 .
.
или
 , (20)
, (20)
где ![]() ;
; ![]() , тогда
, тогда ![]() ;
; ![]() ;
;  (21)
(21)
Запишем 
и найдем ![]() ,
,
где  ;
; ![]() ;
; .
.
В этом случае выражение для потенциальной энергии в развернутой форме в координатах ![]() ,
, ![]() и
и ![]() определится
определится
 (22)
(22)
где  и
и  .
.
В таблице 4 представлены значения коэффициентов уравнений системы (рис.1) в координатах ![]() ,
, ![]() и
и ![]()
Значения коэффициентов уравнений в координатах ![]() ,
, ![]() и
и ![]()
Табл. 4
|
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
| 0 |
|
Обобщенные силы по координатам ![]() ,
, ![]()
![]() и имеют вид
и имеют вид
![]() ;
;![]() ;
;![]() . (23)
. (23)
В этой системе координат ![]() ,
, ![]() и
и ![]() возможно также введение сочленения и по координате
возможно также введение сочленения и по координате ![]() . Для получения передаточной функции системы, которая имеет две степени свободы
. Для получения передаточной функции системы, которая имеет две степени свободы ![]() и
и ![]() необходимо исключить соответствующие столбцы и строку. Отметим, что, если
необходимо исключить соответствующие столбцы и строку. Отметим, что, если ![]() , то
, то ![]() и движение системы при одном шарнире в точке А, будет описываться координатами
и движение системы при одном шарнире в точке А, будет описываться координатами ![]() и
и ![]() . В данном случае рычаг имеет упругое опирание для своего центра вращения. Наибольший интерес представляет все же случай с двумя сочленениями.
. В данном случае рычаг имеет упругое опирание для своего центра вращения. Наибольший интерес представляет все же случай с двумя сочленениями.
III. Введение двух сочленений. Рассмотрим систему координат ![]() ,
, ![]() и
и ![]() . Вводя ряд соотношений (
. Вводя ряд соотношений (![]() ), запишем выражение для кинетической энергии системы:
), запишем выражение для кинетической энергии системы:
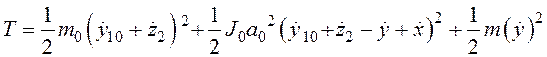 , (24)
, (24)
где  .
.
а также запишем выражение для потенциальной энергии системы
![]() , (25)
, (25)
где ![]()

где ![]() .
.
В табл. 5 приведены коэффициенты уравнений в координатах ![]() ,
, ![]() и x.
и x.
Значения коэффициентов уравнений в координатах ![]() ,
, ![]() и x
и x
Табл. 5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенные силы по координатами ![]() ,
, ![]() и
и ![]() имеют вид
имеют вид
![]() ;
; ![]() ;
;
![]() . (26)
. (26)
При ![]() получим следующие выражении для обобщенных сил:
получим следующие выражении для обобщенных сил:
![]() ; (27)
; (27)
 ; (28)
; (28)
![]() . (29)
. (29)
В данной системе координат имеется возможность выхода на два сочленения: по координате![]() и по координате
и по координате ![]() . Используя матрицу (Табл. 5) и, исключая соответствующие строки и столбцы, получим уравнение движения для системы с двумя сочленениями.
. Используя матрицу (Табл. 5) и, исключая соответствующие строки и столбцы, получим уравнение движения для системы с двумя сочленениями.
![]() . (30)
. (30)
Для упрощения принимаем, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; при этом
; при этом ![]() , тогда уравнение (30) преобразуется к виду
, тогда уравнение (30) преобразуется к виду
![]() , (31)
, (31)
откуда передаточная функция системы принимает вид
 . (32)
. (32)
Сравнение (32) и (8) показывает, что структура передаточных функций является общей и предлагаемый подход позволяет построить необходимые математические модели.
Для получения полного совпадения результатов необходимо представить расчетную схему более детализированной. Для вывода (8) использовалась схема, показанная на (рис.2). Особенность этой расчетной схемы заключается в учете массоинерционных свойств рычажных связей. Рассмотрим, в связи с этим расчетную схему системы на рис.3.4, которая отражает массоинерционные свойства системы. На расчетной схеме (рис.5) показаны массы ![]() и
и ![]() ; учет особенностей их движения является существенным фактором для совпадения выражений (8) и (32).
; учет особенностей их движения является существенным фактором для совпадения выражений (8) и (32).

Рис. 5. Расчетная схема ВЗС на рис.1, но с разнесенными массами ![]() и
и ![]()
Выберем для дальнейших расчетов систему координат ![]() ,
, ![]() и
и ![]() , полагая при этом, что
, полагая при этом, что ![]() ,
,![]() где
где ![]() . Запишем выражения для кинетической и потенциальной энергий системы
. Запишем выражения для кинетической и потенциальной энергий системы
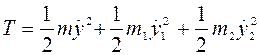 , (33)
, (33)
 (34)
(34)
Произведем ряд преобразований:
![]() ,
,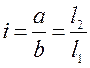 ;
;  ;
;
![]() , (35)
, (35)
тогда получим (33), (34) в виде
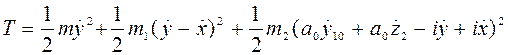 , (36)
, (36)
![]() (37)
(37)
где ![]() . Сделав ряд вспомогательных выкладок, аналогичных выше приведенным при выводе уравнений движения, получим уравнения движения в виде
. Сделав ряд вспомогательных выкладок, аналогичных выше приведенным при выводе уравнений движения, получим уравнения движения в виде
 (38)
(38)
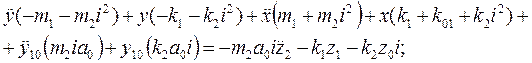 (39)
(39)
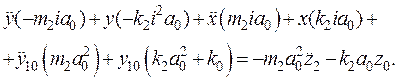 (40)
(40)
В табл.3.5 приведены коэффициенты уравнений (38) ÷ (40).
Значения коэффициентов уравнений в координатах ![]() ,
, ![]() и
и ![]()
Табл. 6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенные силы в данном случае имеют вид
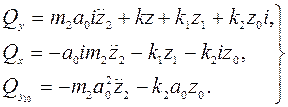 (41)
(41)
Исключая из матрицы столбцы и строки по координатам ![]() и
и ![]() , получим уравнение движения для системы с координатой
, получим уравнение движения для системы с координатой ![]()
![]() . (42)
. (42)
Для построение передаточной функции «смещение ![]() по входу
по входу ![]() » примем, что
» примем, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В этом случае при
. В этом случае при ![]() ,
, ![]() , тогда
, тогда
 , (43)
, (43)
Отметим, что 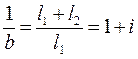 ; в этом случае
; в этом случае
 . (44)
. (44)
Выражения (8) и (44) полностью совпадают, что собственно и требовалось доказать.
Заключение. 1. Таким образом, выбирая систему обобщенных координат соответствующим образом, можно построить математическую модель механической системы с сочленениями. В этом случае система с сочленениями обладает меньшим числом степеней свободы, чем у исходной системы. Сочленение возможно между двумя телами при соединении двух тел в кинематическую пару вращательного вида (V класса). Однако, возможны и соединения твердого тела и с другим телом с потерей возможности относительного движения.
2. Предлагаемый метод получения математических моделей обладает возможностями реализации посковых технологий в разработке новых способов и средств защиты объектов от вибрационных воздействий.
3. Особенности метода таковы, что при выборе систем координат исходной системы и числа сочленений, их форм и мест расположения, что позволяют получать семейства технических решений, из которых могут быть выделены схемы, представляющие интерес для решения конкретных задач динамики машин.
Библиографический список
1. Упырь Р.Ю. Динамика механических колебательных систем с учетом пространственных форм сочленений элементарных звеньев.: автореф. … канд. техн. наук / Р.Ю. Упырь 0 Иркутск.: ИрГУПС. – 2009. 19 с.
2. Елисеев С.В., Резник Ю.Н., Хоменко А.П. Мехатронные подходы в задачах динамики колебательных систем. – Новосибирск.: Наука. 2011. – 394 с.
3. Лурье А.И. Аналитическая механика. – Москва.: Наука. 1986. – 560 с.
4. Хоменко А.П., Елисеев С.В. Сочленения в виброзащитных системах как процесс уменьшения числа степеней свободы движения // Современные технологии. Системный анализ. Моделирование. Вып. № 4(28) – Иркутск.: ИрГУПС. 2010. – с. 8-15
5. Трофимов А.Н. Об оценке свойств вычажных динамических гасителей колебаний // Системы. Методы. Технологии. Вып. № 3(11) – Братск.: БрГУ. 2011. – с. 45-60
Публикации с ключевыми словами: сочленение твердых тел, математические модели механических колебательных систем, режимы динамического гашения колебаний
Публикации со словами: сочленение твердых тел, математические модели механических колебательных систем, режимы динамического гашения колебаний
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||