научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0370692
УДК 543.8+541.13
Россия, МГТУ им. Н.Э. Баумана
Цель исследования. Работы, связанные с исследованием прочности жидкостей на разрыв в статическом и динамическом режимах растяжения многочисленны и разнообразны по технологиям испытаний. Ранее широко практиковался метод Бертоле [4, 7, 11, 14, 15], в котором использовался стеклянный или стальной капилляр, оба конца которого запаивались после частичного заполнения под вакуумом исследуемой дегазированной жидкостью. При нагревании до определённой температуры жидкость расширялась и заполняла весь объём капилляра. После медленного охлаждения капилляр оставался полностью заполненным жидкостью до тех пор, пока не происходил разрыв жидкости под действием растягивающих усилий, обусловленных объёмным сжатием. Анализ диапазона изменения температуры при нагреве и разрыве жидкости с учётом коэффициентов теплового расширения материала капилляра и жидкости давал оценку напряжения растяжения в момент разрыва жидкости. Винсент Р. [16], используя стеклянный капилляр Бертоле, получил значение прочности на разрыв минерального масла равное 12 МПа. По второму методу, Винсент заполнял минеральным маслом глухой металлический сильфон, который затем медленно растягивался до разрыва жидкости, сопровождаемого резким изменением объёма: прочность на разрыв составила всего 0,3 МПа. Используя вязкостный тонометр (длинный стеклянный капилляр, соединённый со стеклянной колбой), Винсент получил для минерального масла прочность на разрыв 0,8 МПа [18]. По методу Бриггса Л. [5] длинный стеклянный капилляр заполнялся исследуемой жидкостью, разрезался на куски ограниченной длины (с открытыми концами), погружался в подогреваемую ванну («жидкостную баню»), заполняемую другой, не смешивающейся с исследуемой, жидкостью. В процессе перегрева исследуемой жидкости в ней создавались напряжения растяжения и жидкость разрывалась. Давление насыщенного пара при температуре разрыва принималось за меру напряжения разрыва. Ускоренный динамический разрыв жидкости был осуществлён Дэвисом Р. [6] в стальной трубке, заполненной жидкостью и закрытой с обеих сторон поршнями с малой массой. После выстрела в один из поршней свинцовой пулей в жидкости возникал гидроудар. В условиях полной прилипаемости жидкости к поверхности поршня, гидроудар вызывал в жидкости растягивающие напряжения, которые оценивались с учётом масс поршней, плотности исследуемой жидкости, скорости распространения ударной волны и частотных характеристик процесса изменения давления: для воды было получено среднее значение напряжения растяжения 0,9 МПа.
Значительный разброс полученных экспериментальных данных, сложность проведения исследований, отдалённость методов исследования от задач расчёта и проектирования гидравлических машин и устройств гидроавтоматики, побудили автора статьи использовать другой, более простой метод исследования разрывной прочности минерального масла.
Физические основы кавитации. Частицы рабочей жидкости (жидкости, в объёме которой присутствуют мелкодисперсные пузырьки нерастворённого газа и механические примеси), заполняющей некоторый объём камеры, удерживаются вместе силами внешнего абсолютного давления и межмолекулярного воздействия, при этом объём жидкости может быть полностью или частично ограничен твёрдыми стенками камеры. Гидроцилиндр представляет собой замкнутую камеру, в которой жидкость ограничена поршнем, боковой цилиндрической поверхностью и дном (крышкой) гидроцилиндра. Сосуд без крышки представляет собой открытую камеру, в которой жидкость ограничена дном и стенками сосуда, а также поверхностью раздела «жидкость-газ».
Снижение абсолютного давления в жидкости, определяющего величину напряжения сжатия, возможно двумя способами:
- в открытой камере уменьшение напряжения сжатия достигается путём создания вакуума на поверхности жидкости (поверхностное вакуумирование);
- в замкнутой камере аналогичный эффект может быть достигнут путём увеличения объёма поршневой полости при выдвижении штока в условиях прилипания жидкости к поршню и дну цилиндра.
В обоих случаях появление в жидкости растягивающих усилий (напряжений растяжения) возможно только тогда, когда абсолютное давление станет алгебраически меньше нуля, т.е. станет растяжением [8, 12]. В дальнейшем, под разрывной прочностью жидкости будем понимать такое абсолютное давление, создаваемое в жидкости одним из упомянутых выше способов, в условиях которого жидкость перестаёт быть сплошной средой и из неё начинают выделяться паровые, газовые или паро-газовые пузырьки. Именно абсолютным давлением начала выделения пузырьков будет оцениваться разрывная прочность реальной жидкости, хотя можно прогнозировать уменьшение абсолютного давления при полном разрыве сплошности среды. В реальной, специально не подготовленной рабочей жидкости, всегда присутствует растворённый и нерастворённый газ или смесь газов (воздух). В идеальной, полностью дегазированной и очищенной от механических примесей жидкости, в которой частицы могут находиться рядом только под воздействием сил межмолекулярного взаимодействия в условиях нулевого значения внешнего абсолютного давления, разрыв жидкости в замкнутой камере возможен лишь в том случае, когда внешнее растягивающее усилие, создаваемое поршнем с прилипшей к нему жидкостью, а также приведённая к единице площади поршня сила поверхностного натяжения в условиях полной смачиваемости стенки, превысят удельную силу межмолекулярного взаимодействия и жидкость начнёт вести себя как жидкий стержень.
В расчётах гидравлических систем управления принято допущение, при котором рабочая жидкость разрывается при абсолютном давлении равном или близким к давлению насыщенных паров [3]. В реальных рабочих жидкостях, в частности в маслах на минеральной основе, в которых в той или иной степени присутствует как растворённый в межмолекулярном пространстве, так и нерастворённый в виде мельчайших пузырьков воздух, разрыв жидкости произойдет при более высоких значениях абсолютного давления (меньшем значении вакуума).
Растворённый воздух, который сам по себе не влияет на разрывную прочность жидкости, при понижении абсолютного давления, в соответствии с законами Дальтона и Генри, покидает межмолекулярное пространство и становится генератором кавитационных ядер - мельчайших пузырьков нерастворённого воздуха, которые, укрупняясь, превращаются в каверны. Микронеровности и трещины на поверхности твёрдых стенок камеры, а также частицы механических примесей, играют роль слабых точек, в которых образуются и удерживаются ядра разрывных полостей.
С понятием разрывной прочности жидкости хорошо согласуется явление кавитации – двухфазный процесс, связанный с выделением из жидкости пузырьков газа (пара), образованием каверн в области пониженного абсолютного давления (первая фаза), и с последующим смыканием и сжатием этих пузырьков в области повышенного абсолютного давления (вторая фаза). В этом случае разрыв жидкости можно рассматривать как первую фазу этого процесса. Если после разрыва жидкости в ней длительное время поддерживается абсолютное давление ниже критического значения, определяемого физическими свойствами и состоянием жидкости, то в ней устанавливается устойчивая кавитация в своей первой фазе [8].
Равновесные микропузырьки газа округлой формы диаметром менее 1÷2 мкм присутствуют в любой, не прошедшей специальную обработку (дегазацию), жидкости. Увеличение размеров пузырька может происходить с умеренной скоростью, если оно обусловлено диффузией в него растворённого в жидкости газа, или медленным объёмным расширением жидкости, вызывающим понижение в ней абсолютного давления. Спонтанное развитие парогазовых каверн происходит, когда внутрь пузырька врывается пар. В технической гидродинамике под кавитацией подразумевают развитие пузырьков при гидродинамическом понижении абсолютного давления, связанного с увеличением скоростного напора в сжатом сечении потока в соответствии с уравнением Д. Бернулли: не корректно термином кавитация заменять понятие кипения жидкости в открытой камере, вызванное ростом пузырьков под действием температуры и повышением давления насыщенных паров до значения абсолютного давления на поверхности жидкости. Рост пузырьков, обусловленный диффузией в них растворённого в жидкости газа при статическом или динамическом понижении абсолютного давления и последующее удаление этих пузырьков из жидкости называется дегазацией (деаэрацией применительно к воздуху).
Согласно элементарной теории кавитации разрыв идеальной жидкости, т.е. первая фаза кавитации, связанная с образованием каверн, начинается, когда местное абсолютное давление в жидкости падает до значения давления насыщенных паров и обусловлен процессом испарения. В реальной рабочей жидкости величина абсолютного давления начала кавитации больше, что связано с наличием в жидкости устойчивых кавитационных ядер. Таким образом, первая фаза кавитация характеризуется разрывной прочностью жидкости при заданной температуре, она вторична по отношению к стадии разрыва жидкости, количественно связана с испаряемостью жидкости или спонтанным расширением пузырька нерастворённого газа. Давление насыщенных паров, при котором полностью дегазированная жидкость претерпевает разрыв, является мерой внутреннего напряжения, возникающего в момент разрыва. При очень быстром, практически мгновенном разрыве дегазированной жидкости, алгебраическая величина абсолютного давления становится меньше нуля и в жидкости возникают кратковременные напряжения растяжения.
В замкнутой камере нарушение сплошности среды определяется напряжениями, связанными с прочностью жидкости на разрыв, если сила прилипания жидкости к твёрдой стенке больше разрывного усилия, или отрывом жидкости от стенки (пристеночная кавитация). Если смачиваемость недостаточна для удержания слоя жидкости на стенке (гидрофобные поверхности), то кавитационные ядра образуются на поверхности стенки раньше, чем наступает первая фаза кавитации в объёме жидкости, и разрыв наступает при более высоких значениях абсолютного давления. В случае полного отсутствия нерастворённого воздуха, разрывная прочность при медленном понижении абсолютного давления определяется только испаряемостью жидкости-она приобретает более высокую прочность на разрыв, если была предварительно подвергнута опрессовке под высоким давлением с последующей дегазацией.
Как было отмечено выше, в жидкости, находящейся в абсолютном покое в поле силы тяжести, долгое время могут присутствовать мелкодисперсные пузырьки нерастворённого воздуха, размеры которых не превышают 1÷2 мкм и которые не могут всплыть под действием естественной флотации, условия которой определяются плотностью и вязкостью жидкости. В тоже время, диаметры пузырьков должны быть достаточно малыми, чтобы давление внутри пузырька, определяемое коэффициентом поверхностного натяжения и размерами пузырька, было выше давления, при котором жидкость была насыщена газом. Если присутствует физическая возможность естественной флотации, то разрывную прочность жидкости можно оценивать двумя величинами: абсолютным давлением начала зарождения видимых невооружённым глазом пузырьков и абсолютным давлением, при котором начинается их естественная флотация или спонтанное развитие каверн.
О росте микропузырька. Проблемы, связанные с развитием ядра и его превращением в каверну, были впервые рассмотрены Рэлеем [13] и затем подробно изучены Кнэппом [8].
Пренебрегая силой тяжести газа, заполняющего пузырёк, статическое равновесие пузырька можно представить уравнением
Pж + Ps - Pг = 0 (1),
где Рж = р0πR2 - сила давления жидкости на криволинейную поверхность полусферы; Рs = 2πRσ - сила поверхностного натяжения; σ - коэффициент поверхностного натяжения; Рг = Pпл.ст. = ( рп + рг )× πR2 - сила давления насыщенного пара и нерастворённого газа на газовую плоскую стенку; р0 - давление жидкости на поверхности пузырька; рп - давление насыщенного пара при заданной температуре; рг - парциальное давление газа; R– радиус сферической поверхности пузырька.

После подстановки значений сил уравнение (1) в напряжениях принимает вид
р0 = рп + рг - 2σ /R (2).
Если газ, заполняющий сферический пузырёк, считать совершенным, давление насыщенного пара рп = рп (Т), (где Т- абсолютная температура) независящим от радиуса, а процесс диффузии через границу раздела «газ-жидкость» постоянным, то состояние газа определяется уравнением Менделеева – Клапейрона
рп = MRгT/V = 3MRгT/ 4πR3 = NT/R3 (3),
где N = 3MRг/4π - постоянная фиксированной массы газа в объёме пузырька; Rг – газовая постоянная; V– объём сферического пузырька. После подстановки давления (3) в уравнение (2) получим
р0 = рп + NT/R3- 2σ/r0 (4).
Допуская радиальное движение жидкости относительно центра пузырька безвихревым (от центра при растяжении пузырька и к центру при его сжатии) и имеющим потенциал скорости φ = R2 r × dr dt, гдеR = R(t) – радиус сферической поверхности пузырька; r- текущий радиус внутреннего объёма пузырька (0 ≤ r ≤ R), радиальную составляющую скорости движения жидкости относительно центра пузырька можно выразить через потенциал скорости
U = -∂φ ∂t= R2 r2 ´ dRdt (5),
где dRdt = u0 – радиальная скорость расширения (сжатия) поверхности пузырька, равная скорости движения жидкой частицы, лежащей на стенке пузырька. Пренебрегая силой тяжести массы газа внутри пузырька и принимая плотность частицы жидкости квазистационарной r = inv, уравнение движения жидкости представим в виде
-∂φ ∂t + u2 / 2 + p / r = p∞/ ρ (6),
где р = р(r,t) – местное давление в жидкости, находящейся в окрестностях пузырька;
р∞ = р∞(t) – давление в жидкости, достаточно удалённой от поверхности пузырька с
u = 0, φ = 0. На радиусе r = R частица жидкости движется под действием сил давления с радиальной скоростью, равной скорости движения стенки пузырька u0
-Rdu0 dt- 3u02 / 2 = (p∞-p0) / ρ (7).
Совместное решение уравнений 4, 6, 7 определяет выражение результирующей силы, под действием которой изменяется радиус пузырька
F(R,T) = ρ(Rdu0 / dt + 3u02 / 2) = pп -р¥ + NT / R3- 2σ/R (8).
При F(R,T) = 0 устанавливается баланс напряжений
рп-р∞ + NT / R3 - 2σ / R = 0 (9),
при этом радиус пузырька принимает равновесное значение R = Re.
Если F(R,T) > 0, то пузырёк расширяется, а при F(R,T) < 0 – сжимается.
В соответствии с равенством (9) пузырёк может расти с умеренной скоростью в четырёх случаях:
-при диффузии растворённых газов через стенку пузырька (∆N > 0);
-при расширении содержащегося в пузырьке газа, обусловленном повышением температуры (∆T > 0);
-при увеличении давления насыщенных паров, вызванным нагревом жидкости (∆рп > 0);
-при появлении в жидкости растягивающих напряжений (∆σраст = - р∞ > 0).
В соответствии с принятым понятием кавитации, её появление обусловлено только растягивающим напряжением и равенство (9) принимает вид
σраст = 2σ Rе- рп -NT / Rе3 (10),
где, как и прежде, Rе – равновесный радиус пузырька.
В сечении, удалённом от зоны дросселирования, давление жидкости может быть достаточно большим, а радиус пузырька малым из-за растворения газа в жидкости в соответствии с законом Генри
Vг = αVж рг / pатм (11),
где Vг – приведённый к атмосферному давлению ратм объём газа, который может раствориться в объёме жидкости Vж под давлением рг.
Принимая для минеральных масел при Т = 293К (Т0С = 200С); рг = рп = 1000Па; σ = 0,1 Нм и начальный радиус ядра Rе = Rmin = 0,01 мкм = 10-8 м, что на порядок больше наблюдаемого размера пузырька R = 10-9 м, отмеченного в работе [2], можно оценить порядок величины напряжения растяжения жидкости в начальной стадии кавитации σраст = 2σ / Rе - 2рп = 20 МПа. Рост пузырька прекращается, когда начинает выполняться условие σраст = 0 и при рп = рг = 1000 Па устанавливается равновесный радиус пузырька Rе = Rmax = 0,1 мм.
При сравнительно небольшой скорости движения стенки пузырька в процессе его расширения dRе>0 поглощаемое газом тепло компенсируется подводом тепла из окружающей пузырёк жидкости и процесс расширения газа близок к изотермическому Rе3 = рг maxRmin3, или pг = pг max × (Rmin / Rе)3 = pг max × (R*)3, где R* = Rmin / Rе – безразмерный радиус пузырька.
Подставляя в уравнение (2) начальное значение давления газа в пузырьке ргmax при R = Rmin, получим рг max = p0 - pп + 2σ / Rmin = pг / (R*)3 и снижение давления газа в пузырьке при его расширении будет соответствовать уравнению рг = (р0 - рп + 2σ / Rmin)×(R*)3, где p0 – давление жидкости на поверхности пузырька. В соответствии с выражением (9) равновесное давление в жидкости, достаточно удалённой от поверхности пузырька, подчиняется зависимости
р∞ = рп + (р0-рп + 2σ/Rmin)´(R*)3 - 2σ/Rе (12).
При быстром движении стенки при расширении пузырька (dRе > 0) процесс теплообмена между расширяющимся газом и окружающей его жидкостью прекращается и уравнение состояния газа соответствует адиабатическому закону с показателем политропы к = 1,4. В этом случае рг = рг max (Rmin / Rе)3к = рг max (Rmin / Rе)4,2.
Вязкость жидкости демпфирует рост ядра кавитации и замедляет флотацию, что приводит к длительному существованию ядер кавитации в вязких жидкостях. Растворённый в жидкости воздух сам по себе не оказывает влияние на её разрывную прочность [9]. При благоприятных условиях время образования каверны достаточно мало (примерно 5 мс) и его недостаточно для активной диффузии растворённого воздуха через жидкость к поверхности раздела «каверна-жидкость». При быстром закрытии каверны содержащийся в ней воздух не успевает полностью раствориться, а его избыток при дроблении каверны идет на генерирование новых ядер и активизацию кавитации. В работе [2] отмечается, что объём каверны при первом повторном её зарождении составляет 65 % объёма первообразной каверны, что приводит к образованию не одной вторичной каверны того же размера, а к сообществу более мелких пузырьков.
О роли растворённого воздуха. В соответствии с законом Дальтона [3] в единице объёма жидкости Vж может находиться строго определённое количество растворённого воздуха Vв до её полного насыщения
Vв = α×Vж ×p1 / ( p1 - ∆p),
где α– коэффициент растворимости (для воздуха в минеральном масле α = 0,10); p1 – давление газа при полном насыщении жидкости; ∆p – уменьшение давления до нового уровня, при этом под Vв подразумевается объём воздуха при атмосферном давлении, который может раствориться в жидкости при повышении первоначального давления на величину ∆p>0, или выделиться из жидкости в виде процесса насыщения жидкости воздухом в объёме Vж характеризуется соотношением S/Vж, где S – площадь поверхности раздела двух сред. Скорость растворения воздуха не постоянна: 25 % возможного объёма Vв растворяется практически мгновенно из-за насыщения поверхностных слоёв жидкости, а остальные 75 % растворяются в процессе медленной диффузии. При резком нарастании давления ∆p > 0 мелкие и средние пузырьки растворяются практически мгновенно. Выделение растворённого воздуха из жидкости более интенсивно, по сравнению с его растворением при том же значении ∆p. Особенно интенсивным является выделение растворённого воздуха при гидродинамической кавитации в узких щелях дросселирующих устройств. С учётом вышеизложенного, альтернативный процесс сжатия и расширения жидкости с последующей её кавитацией при резком понижении гидродинамического давления приводит к образованию двухфазной среды «жидкость-нерастворённый воздух».
Экспериментальная установка для исследования разрывной прочности минерального масла. Исследование разрывной прочности минерального масла было выполнено на экспериментальной установке, гидравлическая схема которой представлена на рис. 1а (см. также фотографии, представленные на рис. 2а, 2б, 2в, 2г). Вакуум в кавитационной камере 3 создавался поршневым вакуумным насосом 2 с пневмоприводом. Кавитационная камера непосредственно насажена на штуцер поршневой полости вакуумного насоса и представляет собой стеклянный цилиндр с внутренним диаметром 12 мм и длиной 160 мм (короткая камера) или 650 мм (удлинённая камера).
Для ускоренного заполнения кавитационной камеры при прямом ходе поршня вакуумного насоса открываются регулируемые дроссели 5 и 7. Проливка кавитационной камеры осуществляется при обратном ходе поршня через обратные клапаны 6, 10 линии байпаса при закрытом дросселе 7 в верхнюю часть бака, что позволяет отвести пузырьки нерастворённого воздуха в атмосферу через сапун. Исследование разрывной прочности минерального масла осуществляется при закрытом дросселе 5 после завершения процесса проливки кавитационной камеры и её полного заполнения.
Для обеспечения минимума присоединённого объёма поршневой полости вакуумного насоса 2 при испытании жидкости на разрыв его поршень должен находиться в крайнем положении. Скорость вакуумирования кавитационной камеры настраивается регулируемым дросселем 15 пневмопривода после подачи напряжения питания на электромагнит S2 пневматического распределителя 17. В целях предотвращения проникновения в кавитационную камеру воздуха из штоковой полости вакуумного насоса 2 при вакуумировании предусмотрен гидравлический затвор с компенсационным баком 4.
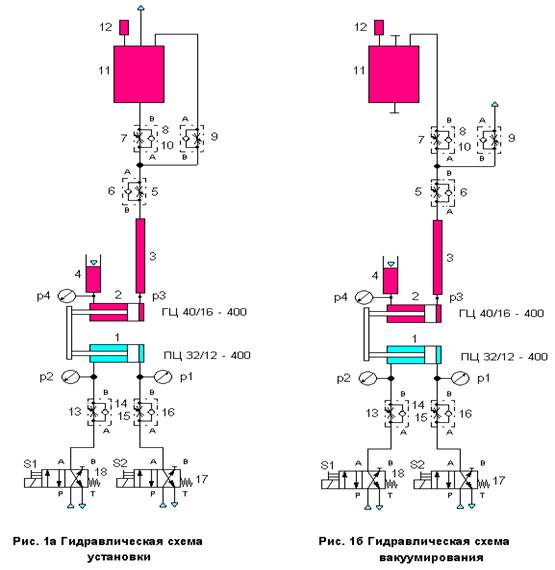

Рис. 2а. Экспериментальная установка (панель управления)

Рис. 2б. Вакуумный насос с пневмоприводом и кавитационная камера

Рис. 2в. Вакуумный насос с пневмоприводом

Рис. 2г. Короткая кавитационная камера

Рис. 3. Визуализация процесса
Визуализация и съёмка процессов гидродинамической дегазации и разрыва минерального масла в кавитационной камере осуществляется цифровой видеокамерой с короткофокусным объективом (рис. 3) и анализируется на компьютере..
Для удаления из объёма минерального масла растворённого в нём воздуха возможно применение трёх технологий дегазации:
- гидростатическая поверхностная дегазация в соответствии с гидравлической схемой рис. 1б, когда над поверхностью минерального масла в баке 11, при закрытом сапуне 12, вакуумным насосом создаётся и поддерживается вакуум (этот вид дегазации длителен и мало эффективен);
- гидродинамическая дегазация в соответствии с гидравлической схемой рис. 1а, когда при сравнительно медленном заполнении кавитационной камеры в дросселе 5 возникает кавитация [1] с активным выделением растворённого воздуха, который вытесняется в верхнюю часть бака в процессе проливки кавитационной камеры через обратный клапан 10 байпаса при закрытом дросселе 7 линии заполнения кавитационной камеры;
- разрывная дегазация, когда при быстром вакуумировании кавитационной камеры в ней резко падает абсолютное давление [2], что приводит к спонтанному развитию крупных паро-воздушных каверн, которые при быстром обратном ходе поршня вакуумного насоса вытесняются в бак через обратный клапан 10 байпаса при закрытом дросселе 7. Наиболее эффективны две последние технологии дегазации.
В целях сведения к минимуму величины присоединённого к кавитационной камере вредных объёмов, в экспериментальной установке не мог быть использован пружинный вакуумметр, и оценка величины абсолютного давления p3 в процессе вакуумирования кавитационной камеры и разрыва жидкости осуществлялась косвенным способом, путём пересчёта избыточного давления p1в поршневой полости пневмоцилиндра (рис. 4).
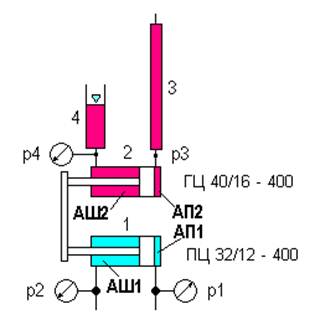
Рис. 4. Расчётная схема определения абсолютного давления в кавитационной камере
Уравнение равновесия механической системы, состоящей из пневмоцилиндра привода 1 и гидроцилиндра вакуумного насоса 2, соединённых силовой траверсой, при равномерном движении поршней в избыточной системе единиц измерения давлений и при p2 = p4 = pат , имеет вид:
p1×Aп1 + ρgh1 ×Aп2- p3 вак×Aп2-ρgh2 ×Aш2-Fтр = 0, (13)
где Fтр , Н – суммарная сила трения в уплотнениях гидроцилиндра вакуумного насоса и пневмоцилиндра пневмопривода вакуумного насоса в момент начала движения; h1 и h2, м– соответственно высоты столбов жидкости в кавитационной камере и гидравлическом затворе. В соответствии с равенством (13) абсолютное давление p3 в нижней части кавитационной камеры определяется выражением
p3 = pат - (p1×Aп1 + ρgh1 ×Aп2 -ρgh2 ×Aш2 -Fтр)/Aп2. (14)
Пробные испытания экспериментальной установки показали, что в условиях эксперимента p2 = p4 = pат, измеренное пружинным динамометром значение суммарной силы трения движения в уплотнениях составляет Fтр = 52H.
С учётом геометрии гидроцилиндра ГЦ 40/16 – 400 и пневмоцилиндра ПЦ 32/12 – 400 формула (14) для удлинённой кавитационной камеры принимает численное значение
p3 = 98,1 × 103 - (8,038 × 10-4×p1 - 46,9 )/12,56 × 10 –4 , Па .
Абсолютное давление в верхней части кавитационной камеры меньше на величину весового давления столба жидкости ρgh1 = 5,48 × 103 , Па
p3 = 98,1 × 103 - (8,04 × 10-4× p1 - 46,9 )/12,56 × 10 –4 - 5,48 × 103 , Па.
Результаты исследования разрывной прочности минерального масла. При малой скорости вакуумирования (выделение из жидкости микропузырьков воздуха наступает через 15÷20 секунд после начала вакуумирования) получены следующие результаты контрольных испытаний:
а) Масло в исходном состоянии (двухнедельный «отдых»):
- значения вакуума и абсолютного давления в нижней части кавитационной камеры при первом появлении микропузырьков нерастворённого воздуха:
p3 вак = 63 кПа; p3 = 35 кПа;
- значения вакуума и абсолютного давления в нижней части кавитационной камеры при появлении крупных каверн и разрыва жидкости:
p3 вак = 83 кПа; p3 = 15 кПа.
б) Масло после 10 циклов гидродинамической дегазации:
- значения вакуума и абсолютного давления в нижней части кавитационной камеры при первом появлении микропузырьков нерастворённого воздуха:
p3 вак = 76 кПа; p3 = 22 кПа;
- значения вакуума и абсолютного давления в нижней части кавитационной камеры при появлении крупных каверн и разрыва жидкости:
p3 вак = 90 кПа; p3 = 8 кПа.
в) Масло после 10 циклов разрывной дегазации:
- значения вакуума и абсолютного давления в нижней части кавитационной камеры при первом появлении микропузырьков нерастворённого воздуха:
p3 вак = 80 кПа; p3 = 18 кПа;
- значения вакуума и абсолютного давления в нижней части кавитационной камеры при появлении крупных каверн и разрыва жидкости:
p3 вак = 94 кПа; p3 = 4 кПа.
Выводы по результатам исследования. 1. Создана и апробирована в работе экспериментальная установка для исследования разрывной прочности рабочих жидкостей для гидроприводов (масел на минеральной основе).
2. Исследованы возможности дегазации минерального масла путём его поверхностного, гидродинамического и разрывного вакуумирования.
3. Получены количественные оценки разрывной прочности минерального масла.
4. Определена зависимость разрывной прочности минерального масла от степени его дегазации методами гидродинамического и разрывного вакуумирования.
Список литературы.
1. Арзуманов Э.С. Кавитация в местных гидравлических сопротивлениях, М., «Энергия», 1978, 302 с.
2. Бахолдин И.Б. Бездиссипативные разрывы в механике сплошной среды. М., «Физматлит», 2004, 318 с., JSB №5-9221-0546-9.
3. Башта Т. М. и др. Объёмные гидравлические приводы. Под ред. Т. М. Башта, М., «Машиностроение», 1968, 628 стр.
4. Bertholet M. Sur quelques phenomenes de dilatation forcee des liquids. Ann.de Chimie et de Physique, 30,322 et Seq.,1850.
5. Briggs L.J. Maximum superheating of water as a measure of negative pressure, Jr. Appl. Phys., 26, 1955.
6. Davies R.M. и др. The tensile strength of liquids under dynamic stressing, Proc. 1955 NPL Symp. on cavitation in hydrodynamics, Paper 5, 1956.
7. Dixon H.H. Note on the tensile strength of water, Sci. Proc. Royal Dublin Soc.,12 (N.S.), 1909.
8. Кнэпп Р., Дейли Дж., Хэммит Ф. Кавитация. Пер. с англ., М., «Мир».1974.
9. Ламекин Н.С. Кавитация: теория и применение, Государственная национальная русская академия, М., «Русаки», 2000, 246 с.
10. Марсден Дж.Э., Чорин А. Математические основы механики жидкости, Пер. с англ., М. , Ижевск: Регулярная и хаотическая динамика, 2004, 203 с.
11. Meyer J., Zur Kenntnis des Negativen Druckes in Flussigkeiten, Abhandl.Deut.BunsenGes. III, №1, 1911.
12. Пирсол И. Кавитация, Пер. с англ.,М., «Мир», 92 с., 1975.
13. Rayleigh, Lord (Strutt J.W.). On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag., 34, 1917.
14. Rees E.P., Trevena D.H. Cavitation thresholds in liquids under static conditions, ASME Cavitation Forum, p.12, 1966.
15. Scott A.F. и др., Study of the Bertholet method for determining the tensile strength of a liquid, Jr. Chem. Phys., 16, 1948.
16. Vincent R.S. Examining of the Bertholet method of measuring tensin in liquids, Proc. Phys. Soc (London), 55,1943.
17. Vincent R.S. The measurment of tension in liquids by means of a metal bellows, Proc. Phys. Soc (London), 55,1943.
18. Vincent R.S. The viscosity tonometer – A new method of measuring tension in liquids, Proc. Phys. Soc (London), 55,1943.
Публикации с ключевыми словами: кавитация, кавитационная камера, кавитационное ядро, вакуумирование, разрывная прочность жидкости, гидродинамическая дегазация, разрывная дегазация
Публикации со словами: кавитация, кавитационная камера, кавитационное ядро, вакуумирование, разрывная прочность жидкости, гидродинамическая дегазация, разрывная дегазация
Смотри также:
- Предвключенное устройство со сверхвысокой всасывающей способностью и низким уровнем низкочастотных пульсаций давления и расхода
- Первые результаты структурного синтеза экспериментальной модели трехрядного конденсатного насоса
- Влияние внешних гидродинамических параметров высокоскоростных подводных аппаратов на их тактико-технические характеристики
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



