научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0369895
УДК 681.31
Россия, МГТУ им. Н.Э. Баумана
При анализе и проектировании структур сложных дискретных устройств таких, как микропроцессорные и робототехнические системы, системы управления технологическими процессами, комплексные автоматизированные системы используется блочно-иерархический метод [1], который предусматривает расчленение процесса проектирования на ряд последовательных уровней и сведение задачи большей размерности к совокупности задач значительно меньшей размерности.
Метод анализа дискретных устройств, формализованных логической сетью, в рамках иерархических уровней проектирования недостаточен, так как не позволяет учитывать такие характеристики дискретного устройства как, например, временные параметры элементов, входящих в модель, а, следовательно, выполнять надежную верификацию проекта. В работах по многоуровневому анализу [2, 3, 4] используется принцип рассмотрения схемы устройства с разной степенью детализации. Предлагаемый в работе метод декомпозиции [5] модели сложной структуры, формализованной в виде функционального блока, позволяет выполнить анализ правильности функционирования сложного дискретного устройства путем автоматического перехода на более низкий иерархический уровень.
Для декомпозиции сложной дискретной структуры необходимо выбрать ортогональное множество разбиений [5].
Поставим в соответствие каждому разбиению ![]() функцию
функцию ![]() , такую, что
, такую, что ![]() , т.е. значение функции
, т.е. значение функции ![]() на паре
на паре ![]() равно блоку
равно блоку ![]() , в котором содержится состояние
, в котором содержится состояние ![]() .
.
Образуем на множествах A и Z соответственно разбиения ![]() и
и ![]() , так что:
, так что:
1. ![]() и
и ![]() находятся в одном блоке разбиения
находятся в одном блоке разбиения ![]() , если и только если для любого
, если и только если для любого ![]() справедливо:
справедливо: ![]() , иначе
, иначе
![]()
2. ![]() и
и ![]() находятся в одном блоке разбиения
находятся в одном блоке разбиения ![]() , если и только если для любого
, если и только если для любого ![]() справедливо:
справедливо: ![]() , иначе
, иначе
![]()
Полученные таким образом ![]() пара разбиений, т.е. каждый блок
пара разбиений, т.е. каждый блок ![]() отображается любым входным сигналом в некоторый блок
отображается любым входным сигналом в некоторый блок ![]() . При этом
. При этом ![]() максимальное разбиение, образующее пару
максимальное разбиение, образующее пару ![]() .
.
Построим логическую сеть ![]() , для чего определим все компоненты кортежа N.
, для чего определим все компоненты кортежа N.
1. Полагаем ![]() .
.
2. Полагаем ![]() .
.
3. Построим функциональные блоки ![]() , т.е. определим базис сети.
, т.е. определим базис сети.
a. Полагаем ![]() .
.
b. Для определения входного алфавита функционального блока ![]() воспользуемся построенными разбиениями
воспользуемся построенными разбиениями ![]() и
и ![]() . Напомним, что
. Напомним, что
 (1)
(1)
Здесь ![]() и
и ![]() соответственно внутренний и внешний входные алфавиты блока
соответственно внутренний и внешний входные алфавиты блока ![]() .
.
Если на вход функции ![]() поступают
поступают ![]() выходы функциональных блоков
выходы функциональных блоков ![]() , то
, то ![]() пара разбиений, где
пара разбиений, где ![]() , так как
, так как ![]() максимальное разбиение, образующее пару с
максимальное разбиение, образующее пару с ![]() . Нетрудно также доказать, что
. Нетрудно также доказать, что ![]() . Таким образом, для нахождения блоков, выходы которых присоединяются ко входу
. Таким образом, для нахождения блоков, выходы которых присоединяются ко входу ![]() , необходимо найти такое произведение
, необходимо найти такое произведение ![]() , которое не превосходит
, которое не превосходит ![]() , и тогда выходы
, и тогда выходы ![]() должны быть соединены со входом
должны быть соединены со входом ![]() .
.
Определим разбиение ![]() следующим образом:
следующим образом:
![]() ,
,
т. е. ![]() не входит в это произведение, так как ко входу
не входит в это произведение, так как ко входу ![]() могут присоединяться выходы других, отличных от
могут присоединяться выходы других, отличных от ![]() , функциональных блоков.
, функциональных блоков.
В блоке ![]() полагаем
полагаем ![]() , а
, а ![]() определяется согласно равенствам (1).
определяется согласно равенствам (1).
c. Определим функцию переходов функционального блока ![]() .
.
Пусть ![]() соответственно блоки разбиений
соответственно блоки разбиений ![]() . Если
. Если ![]() , т. е.
, т. е. ![]() (
(![]() СП-разбиение), то
СП-разбиение), то
![]() .
.
Таким образом, значение функции переходов ![]() равно блоку разбиения
равно блоку разбиения ![]() , содержащему
, содержащему ![]() . Здесь
. Здесь ![]() функция переходов декомпозируемого блока
функция переходов декомпозируемого блока ![]() .
.
Если же ![]() , то
, то
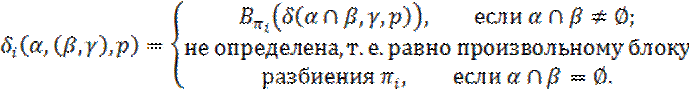
4. Построим функции соединения функционального блока ![]() ; иначе (в терминах разбиений)
; иначе (в терминах разбиений) ![]() .
.
Пусть ![]() . Образуем множество
. Образуем множество ![]() , такое, что
, такое, что ![]() . Таким образом, в
. Таким образом, в ![]() попадают только те векторы из
попадают только те векторы из ![]() , у которых пересечение всех компонентов не пусто. Такое пересечение
, у которых пересечение всех компонентов не пусто. Такое пересечение ![]() имеет место, так как компоненты
имеет место, так как компоненты ![]() блоки разбиений, т.е. множества.
блоки разбиений, т.е. множества.
Функция ![]() реализует отображение
реализует отображение ![]() . Значение
. Значение ![]() определим следующим образом:
определим следующим образом:
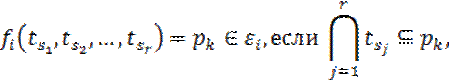
т.е. значение функции ![]() равно тому блоку разбиения
равно тому блоку разбиения ![]() , в который входит пересечение компонентов
, в который входит пересечение компонентов ![]() .
.
На множестве ![]() функция
функция ![]() не определена.
не определена.
5. Определим множество входных функций следующим образом:
![]()
т. е. значение функции ![]() на
на ![]() равно блоку разбиения
равно блоку разбиения ![]() , содержащему
, содержащему ![]() . Отсюда ясно, что автомат
. Отсюда ясно, что автомат ![]() не различают тех букв входного алфавита
не различают тех букв входного алфавита ![]() , которые входят в один блок разбиения
, которые входят в один блок разбиения ![]() .
.
6. Построим выходную функцию сети ![]() , иначе (в терминах разбиений)
, иначе (в терминах разбиений) ![]() .
.
Пусть ![]() . Образуем множество
. Образуем множество ![]() , такое, что
, такое, что ![]() . Таким образом, в
. Таким образом, в ![]() попадают только те векторы из
попадают только те векторы из ![]() , у которых пересечение всех компонентов не пусто.
, у которых пересечение всех компонентов не пусто.
Функция ![]() реализует отображение
реализует отображение ![]() . Значение
. Значение ![]() определим следующим образом:
определим следующим образом:
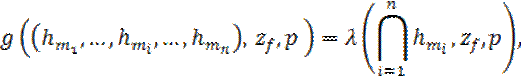
т. е. значение выходной функции сети совпадает со значением функции выхода ![]() декомпозируемого блока
декомпозируемого блока ![]() на паре
на паре ![]() , где
, где ![]() состояние, попавшее в пересечение компонентов вектора
состояние, попавшее в пересечение компонентов вектора ![]() .
.
На множестве ![]() функция
функция ![]() не определена.
не определена.
В работе [5] показано, что построенная таким образом сеть реализует исходный функциональный блок ![]() .
.
Разбиения ![]() и
и ![]() однозначно определяется разбиением
однозначно определяется разбиением ![]()
![]() ;
; ![]() показывает, какие блоки воздействуют на автомат
показывает, какие блоки воздействуют на автомат ![]() , а
, а ![]() определяет классы неразличимых автоматом
определяет классы неразличимых автоматом ![]() букв входного алфавита
букв входного алфавита ![]() .
.
Таким образом, ![]() характеристическая тройка блока
характеристическая тройка блока ![]() . Стоит отметить, что
. Стоит отметить, что ![]() и
и ![]() являются наибольшими разбиениями, причем, чем больше
являются наибольшими разбиениями, причем, чем больше ![]() , тем меньше выходов других блоков воздействует на
, тем меньше выходов других блоков воздействует на ![]() . Чем больше
. Чем больше ![]() , тем проще зависимость
, тем проще зависимость ![]() от внешнего входа
от внешнего входа ![]() . Использование разбиений
. Использование разбиений ![]() и
и ![]() при построении
при построении ![]() является, таким образом, необходимым условием для построения сети
является, таким образом, необходимым условием для построения сети ![]() наименьшей сложности.
наименьшей сложности.
Рассмотрим алгоритм декомпозиции на примере модели сложного дискретного устройства, функционирование которого задано в табличном виде (таблица 1).
Таблица 1.
Пример функционирования дискретного устройства, заданного в виде.
| a1 | a2 | a3 | a4 | a5 | a6 |
z1 | (a1, w2) - 0,5 | (a5, w2) - 0,3 | (a1, w1) - 0,6 | (a6, w1) - 1 | (a1, w3) - 1 | (a2, w2) - 0,6 |
(a2, w1) - 0,5 | (a1, w2) - 0,2 | (a2, w1) - 0,2 |
|
| (a1, w2) - 0,1 | |
| (a2, w2) - 0,3 |
|
|
| (a3, w3) - 0,1 | |
|
|
|
|
| (a4, w3) - 0,1 | |
|
|
|
|
| (a5, w1) - 0,1 | |
z2 | (a6, w2) - 1 | (a1, w1) - 0,2 | (a5, w3) - 0,8 | (a2, w2) - 0,8 | (a1, w1) - 0,3 | (a6, w2) - 1 |
| (a2, w2) - 0,2 | (a2, w3) - 0,1 |
| (a2, w2) - 0,7 |
| |
| (a3, w3) - 0,2 |
|
|
|
| |
| (a4, w3) - 0,2 |
|
|
|
| |
z3 | (a6, w1) - 1 | (a1, w1) - 1 | (a5, w1) - 0,9 | (a2, w2) - 0,6 | (a2, w3) - 0,8 | (a5, w3) - 0,7 |
|
| (a6, w1) - 0,1 |
| (a3, w3) - 0,2 | (a6, w3) - 0,3 | |
z4 | (a2, w3) - 1 | (a5, w3) - 0,7 | (a1, w1) - 0,5 | (a6, w3) - 1 | (a4, w1) - 0,9 | (a3, w1) - 1 |
| (a6, w2) - 0,3 | (a2, w2) - 0,5 |
|
|
|
Устройство содержит в себе как полностью определённые переходы (сумма вероятностей всех возможных исходов из данного состояния при указанном входном символе равна единице) так и частично определённые (сумма вероятностей меньше единицы).
Множество состояний данного устройства ![]() , входной алфавит устройства
, входной алфавит устройства ![]() , выходной алфавит
, выходной алфавит ![]() .
.
В качестве множества ортогональных разбиений возьмём множество ![]() , где
, где
![]()
![]()
![]()
В результате декомпозиции получаем логическую сеть, представленную на рисунке 1.
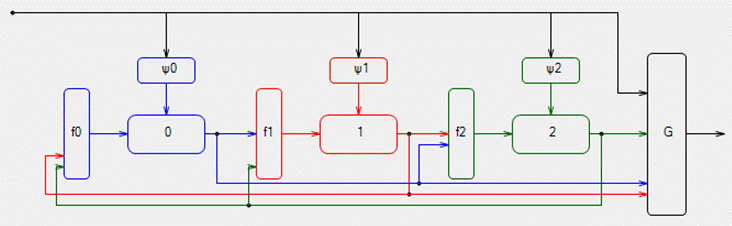
Рисунок 1. Логическая сеть сложного дискретного устройства.
Стоит отметить, что в результате декомпозиции сформировались следующие состояния:
![]()
![]()
![]()
Разработанный алгоритм и основные сущности, связанные с предметной областью, были реализованы в виде .NET-библиотеки, что позволяет использовать её в составе программных комплексов, предназначенных для анализа дискретных систем.
Результаты исследований показали, что в целом алгоритм декомпозиции сложных дискретных устройств обладает необходимой эффективностью. Анализ результатов подтвердил, что при достаточной сложности и определенной топологии системы алгоритм уменьшает время анализа процесса функционирования такого класса устройств в среднем на 25 %, причем также уменьшается общая вероятность ошибки в системе (порядка 30%) в силу подробного просмотра и анализа каждой подструктуры.
Данный алгоритм декомпозиции практически использовался при моделировании автомобильного потока для анализа чрезвычайных ситуаций в туннелях транспортного типа.
Литература
1. Норенков И.П. Основы автоматизированного проектирования: Учеб. для вузов.-М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.- 360 с.
2. Воротников С.А. Информационные устройства робототехнических систем. Уч. пособие – .-М.: Изд-во МГТУ им. Н.Э. Баумана, 2005.- 384 с
3. Рудаков И.В., Смирнов А.А. Исследование сложных дискретных систем на базе агентного метода. Статья. Вестник МГТУ им. Н.Э. Баумана – Сер. Приборостроение.-М.: МГТУ, 2009.-№3-С. 33-41.
4. Рудаков И.В., Давудпур М. Алгоритм декомпозиции формальной модели функционального блока дискретного устройства. Статья. Вестник МГТУ им. Н.Э. Баумана – Сер. Приборостроение.-М.: МГТУ, 2006.-№1-С. 90-98
5. Рудаков И.В., Давудпур М. Декомпозиционный метод исследования дискретных устройств. Статья. Информационные технологии.-М.2006.-№2-С.44-49
Публикации с ключевыми словами: декомпозиция, сложные технические системы, дискретные устройства, логическая сеть
Публикации со словами: декомпозиция, сложные технические системы, дискретные устройства, логическая сеть
Смотри также:
- Методика иерархического исследования сложных дискретных структур
- 77-48211/465152 Математические модели управляемых процессов: полнота описаний и соразмерность задачам
- 77-30569/292475 Объектно-ориентированное описание предметной области при моделировании процессов ликвидации последствий аварийных разливов нефти
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



