научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2012
DOI: 10.7463/0612.0369542
УДК 681.5.03
Россия, НИУ МИЭТ
Россия, ЗАО «НТЦ ЭЛИНС»
Современные автоматизированные информационные системы (АИС) представляют собой большие сложные многостратные иерархические системы. Система большая – т.к. состоит из большого количества элементов (компонентов); сложная – т.к. процесс принятия решений распределён между уровнями компонентов (подсистемами); многостратная – т.к. включает в себя виды обеспечения различной физической природы: техническое, информационное, методическое, организационное и т.п.; иерархическая – т.к. осуществляется «делегирование полномочий» при распределении функций между компонентами.
Стремление к построению оптимальной по структуре и показателям качества АИС приводит к необходимости развития новых подходов, в частности, методов эволюционного моделирования.
Цель работы - предложить вариант использования многокритериальных генетических алгоритмов оптимизации, основанных на использовании нечетких оценок.
Особенностями задачи нахождения гомеостатического оптимума структуры АИС являются:
- наличие противоречивых критериев оптимальности;
- отсутствие на этапах проектирования достоверных данных о значении и взаимосвязи критериев и управляющих параметров.
Формализация задач оптимизации качества АИС на основе нечётких оценок
Процесс оценивания качества АИС состоит из трех стадий:
-установления требований к качеству в терминах характеристик качества;
-подготовки к оцениванию;
-процедуры оценивания.
После выбора номенклатуры показателей качества на первой стадии процесса оценивания, при подготовке к оцениванию производится выбор шкал, с использованием которых могут быть измерены количественные показатели качества. Однако, измеренное значение не показывает уровень удовлетворения требований. Для этой цели шкала оценок разделяется на диапазоны, соответствующие различным степеням удовлетворения требований. Последним этапом подготовки является выбор формулы оценивания (оценочной функции), в которой учитывались бы результаты оценивания различных показателей.
Обычно оценочная функция, формирующая интегральный показатель качества, имеет вид линейной комбинации значений показателей:

где ![]() - оценка i-ro показателя,
- оценка i-ro показателя,
pi - весовой коэффициент показателя (нормированный: ![]() ),
),
![]() - величина случайная, то есть
- величина случайная, то есть ![]()
где ![]() - «истинное» значение оценки i-ro показателя,
- «истинное» значение оценки i-ro показателя,
σcист - «системная ошибка», связанная с недостатками модели (неточности, внесенные на первых двух стадиях процесса оценивания: при установлении требований к качеству, при выборе метрик, определении уровней ранжирования),
σi - ошибка при проведении процедуры оценивания (третья стадия), вносимая личными качествами эксперта и, возможно, особыми свойствами i-ro показателя.
Учесть системную ошибку (σcист) можно, рассматривая уровень ранжирования как нечеткое множество.
«Индивидуальная» ошибка при оценке каждого показателя (σi) приводит к необходимости интерпретировать значение показателя ![]() как нечеткое значение. Как показано в [1], в случае применения нечеткого подхода, достоверность интегрального показателя при экспертном методе оценки значений критериев выше, чем достоверность показателя, полученного обычным путем.
как нечеткое значение. Как показано в [1], в случае применения нечеткого подхода, достоверность интегрального показателя при экспертном методе оценки значений критериев выше, чем достоверность показателя, полученного обычным путем.
Рассмотрим шкалу оценок, на которой выделены следующие уровни ранжирования значений показателей качества - степени удовлетворения требований:
-низкий;
-средний;
-хороший;
-высокий.
Предлагаемая шкала оценок (рис. 1) представляет собой шкалу метрик (х) в интервале от 0 до 1, которая равномерно разделена на уровни ранжирования - промежутки одинаковой длины (по 0,25).

Рисунок 1 - Шкала уровней ранжирования
Количественное значение показателя качества (х) характеризует субъективное мнение эксперта о принадлежности х одному из уровней ранжирования.
Функция принадлежности уровню зависит от параметров а - центр и b – разброс (функция Харрингтона)
 ),
),
![]()
Характеристики уровней приведены в таблице 1.
Таблица 1 - Характеристики уровней
Уровень | Нечеткое множество (а, b) |
Низкий |
|
Средний |
|
Хороший |
|
Высокий |
|
Тогда функция принадлежности для всей шкалы уровней оценки качества будет выглядеть следующим образом (рис. 2):

Рисунок 2 - Нечеткие множества «Низкий», «Средний», «Хороший» и «Высокий» на шкале уровней
Модель АИС как объекта оптимизации в терминах популяционной генетики
Первым шагом при построении модели объекта оптимизации является выбор некоторого представления объектов из пространства альтернатив X. Представление определяется множеством S из пространства представлений. S выбирается с таким расчетом, что алгоритму поиска будет легче манипулировать членами S, чем X. Как правило, S не равно X, хотя это и не всегда обязательно.
В отличие от пространства объектов, множество S обязательно конечное. Отображение между элементами X и S будем называть представлением. Представление описывает связь между исследуемыми объектами, которые выступают в качестве потенциальных решений задачи поиска, и объектами, которыми манипулирует поисковый алгоритм. Представление есть функция кодирования:
![]()
Для ![]() и
и ![]() запись
запись ![]() будет обозначать, что s является представлением х. Обратное отношение будем записывать как
будет обозначать, что s является представлением х. Обратное отношение будем записывать как ![]() (функция декодирования):
(функция декодирования):
![]()
Обратное отношение используется тогда, когда по новому представлению ![]() , полученному в результате поиска, требуется восстановить соответствующее ему решение
, полученному в результате поиска, требуется восстановить соответствующее ему решение ![]() . Если
. Если ![]() , то будем говорить, что х представлен. Если
, то будем говорить, что х представлен. Если ![]() , то s - недопустимое представление.
, то s - недопустимое представление.
Использование представлений позволяет осуществлять поиск практически при минимуме информации о характере и свойствах пространства объектов. Как правило, бывает достаточно только той информации, которая позволяет описать ландшафт в пространстве представлений.
В классическом ГА альтернатива х обычно кодируется бинарной строкой s. Переход из пространства параметров в хеммингово пространство бинарных строк осуществляется кодированием значения переменной х в двоичную целочисленную строку длины, достаточной для того, чтобы обеспечить желаемую точность. При этом решением задачи поиска оптимального значения могут быть только дискретные величины. Предлагаемая же нами модель не предусматривает дискретизации, допуская непрерывное изменение параметров, формирующих альтернативу.
Пусть пространство ![]() , где
, где ![]() - множество всех нечетких подмножеств, определенных на вещественной оси, тогда роль функции кодирования
- множество всех нечетких подмножеств, определенных на вещественной оси, тогда роль функции кодирования ![]() может играть N-мерная функция принадлежности нечеткому множеству S, а представление s - степень принадлежности этому множеству. Для того, чтобы была возможность однозначного декодирования представления s в х необходимо, чтобы существовала обратная функция
может играть N-мерная функция принадлежности нечеткому множеству S, а представление s - степень принадлежности этому множеству. Для того, чтобы была возможность однозначного декодирования представления s в х необходимо, чтобы существовала обратная функция ![]() , то есть для нечеткого множества S функция принадлежности ему -
, то есть для нечеткого множества S функция принадлежности ему - ![]() - должна быть непрерывна и строго монотонна.
- должна быть непрерывна и строго монотонна.
Наименьшей единицей биологического вида, подвергающейся воздействию факторов эволюции, является особь. В качестве особи в задаче многокритериальной оптимизации принимается произвольная альтернатива ![]() из пространства альтернатив X. В нашем случае хромосомный набор особи состоит из одной хромосомы, где в роли гена - единицы наследственного материала, ответственного за формирование альтернативных признаков особи, выступает хi - управляемая переменная, которая может принадлежать к одному из возможных типов. Способы представления информации в генах нечеткой особи показаны в таблице 2.
из пространства альтернатив X. В нашем случае хромосомный набор особи состоит из одной хромосомы, где в роли гена - единицы наследственного материала, ответственного за формирование альтернативных признаков особи, выступает хi - управляемая переменная, которая может принадлежать к одному из возможных типов. Способы представления информации в генах нечеткой особи показаны в таблице 2.
Таблица 2 - Способы представления информации в генах нечеткой особи
Ген, si | Характеристика представляемой информации | Способ кодирования |
Числовая переменная | Числа a (например, вещественные, комплексные, целые и т.п.) | Четкое множество с характеристической функцией
|
Интегральная переменная | Интервалы [a,b] – связные ограниченные области действительных чисел | Четкое множество с характеристической функцией
|
Нечеткая переменная 1-го порядка | Нечеткие множества различной природы, в частности, нечеткие числа и интервалы | Функция принадлежности
U - универсальное множество |
Нечеткая числовая переменная | Представляет нечеткие числа – приближенные точечные оценки (например, «приблизительно равен 4») | Унимодальная, нормированная, симметричная функция принадлежности с максимумом в указанном четком числе
|
Нечеткая интервальная переменная | Приближенные интервальные оценки типа «примерно между двумя и пятью» | Нормированная функция принадлежности, принимающая максимальные значения только на указанном интервале
|
Нечеткая переменная n-порядка | Нечеткие переменные порядка n-1. Могут быть представлены варианты вероятностных характеристик, набор различного рода функциональных зависимостей | Функция принадлежности
|
Учитывая, что функция кодирования должна иметь обратную, в тех случаях, когда необходимо использовать для кодирования функцию принадлежности, не обладающую свойством монотонности, кодируемый объект должен быть разбит на подобъекты таким образом, чтобы функция принадлежности оказалась "разрезанной" на монотонные участки.
Таким образом, в многокритериальном ГА нечетких хромосом, особь представляет собой сложную структуру данных, объединяющую представление полей различных типов в единой форме. Каждое поле есть местоположение определенного гена, называемое локусом. Каждый ген может иметь несколько альтернативных форм - аллелей. Хромосома, содержащая в своих локусах конкретные значения аллелей, называется генотипом. Для унихромосомного набора термины «генотип» и «особь» являются синонимами.
Среди различных типов задач поиска наибольший интерес для нас представляет задача, в которой требуется найти лучший, насколько это возможно при существующих ограничениях (временных или каких-либо еще), объект х*. При этом на множестве объектов X должна быть определена критериальная функция у(х), позволяющая сравнивать решения
![]()
такая, что для любых двух х1, х2 из X, при условии у(х1)>у(х2), можно было считать, что альтернатива x1 лучше, чем х2. R - множество вещественных чисел. Очевидно, что об оптимальности того или иного решения можно говорить лишь тогда, когда исследовано все пространство представлений S.
Для реализации алгоритма поиска в пространстве представлений можно ввести функцию оценки представлений, аналогично функции у, определенной на элементах из множества X. Определим ее как
![]() .
.
С помощью К определяется порядок в S таким образом, чтобы представителям лучших объектов в смысле у соответствовало большее значение К. То есть, если для любых двух объектов х1, х2 из X в S определены различные представители s1=(x1) и s2= (x2), s1 не равно s2 и если y(x1)>y(x2), то K(s1)>K(s2). В общем случае, функцией K(s) может быть любая функция М, удовлетворяющая условию:
![]() .
.
Однако, как правило, вполне достаточно сделать
![]()
Иногда, в зависимости от конкретных операторов алгоритма поиска, бывает необходимо, чтобы функция K(s) принимала положительные значения.
Представленные рассуждения позволяют сформулировать задачу поиска наилучшего объекта х* из множества X следующим образом:

Ее решение осуществляется поиском в пространстве S оптимального представления s*:

При взаимодействии особи с внешней средой, ее генотип порождает совокупность наблюдаемых признаков, называемых фенотипом, для целей отбора используется степень приспособленности особи к внешней среде. Фенотип особи есть вектор критериев у=(У1,…Уm). Значения, принимаемые критериями оптимальности в данной точке пространства альтернатив, есть фенотипические признаки особи. Таким образом, каждый критерий оценки альтернативы представляет собой некую зависимость между генотипом и определенным фенотипическим признаком. Степень приспособленности формируется на основе значений критериев.
Критерий так же, как и элемент альтернативы, может представлять собой числовую, интервальную и нечеткую переменную.
Если критерий задает зависимость формулой вида![]() , тo значение в определенной точке вычисляется по правилам произведения алгебраических операций над элементами множества U (например, U=R или U=F(R)).
, тo значение в определенной точке вычисляется по правилам произведения алгебраических операций над элементами множества U (например, U=R или U=F(R)).
Если критерий и оцениваемый параметр есть нечеткие множества различий, то достаточно просто сформировать множество допустимых решений (альтернатив). В общем случае, если имеется n критериев и m ограничений, то множество допустимых решений определяется пересечением всех заданных множеств критериев и ограничений. ![]() . Функция принадлежности для множества допустимых решений соответственно задается соотношением:
. Функция принадлежности для множества допустимых решений соответственно задается соотношением: ![]()
Если принять обозначение ![]() , то соотношение можно записать в виде:
, то соотношение можно записать в виде:
![]() .
.
Поскольку при решении многокритериальной задачи решение, обеспечивающее максимум каждого из частных критериев отыскивается лишь в идеальном случае, требуется компромиссное решение. Поэтому становится необходимым указание последовательности применения критериев и относительной важности критериев.
Классические методы оптимизации (принцип максимума Понтрягина, метод динамического программирования Беллмана и др.) позволяют решать задачи только со скалярным критерием. При наличии векторного критерия применение этих методов оптимизации возможно только путем синтеза (чаще всего аддитивного) одного обобщенного критерия из частных критериев или введением всех (кроме основного) критериев в качестве дополнительных ограничений или штрафных функций, то есть ранжирования критериев.
Таким образом, нечеткий подход к принятию решения - это выбор одной или нескольких из допустимых альтернатив, который осуществляет система принятия решений (СПР), путем формирования из имеющихся критериев, с использованием операций над нечеткими множествами, нечеткого множества предпочтительности Р с функцией принадлежности ![]() .
.
Построение функции предпочтительности на множестве критериев, а не непосредственно на множестве альтернатив объясняется тем, что мощность множества критериев обычно меньше, чем размерность пространства альтернатив, и выявление предпочтений СПР по отдельным критериям несравненно проще, чем по каждой альтернативе.
Наиболее часто при решении многокритериальных задач применяются аддитивный, мультипликативный и минимаксный ![]() способы формирования функции предпочтительности. Для нечеткого подхода следует выделить только два первых способа, так как третий является одним из вариантов второго.
способы формирования функции предпочтительности. Для нечеткого подхода следует выделить только два первых способа, так как третий является одним из вариантов второго.
Аддитивное нечеткое множество предпочтительности Р

определяется следующим образом

где n - число критериев, причем в частном случае могут использоваться и дополнительные условия нормировки
![]() и
и 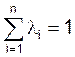
Весовые коэффициенты ![]() для критериев подбираются субъективно, на основе экспертных оценок, однако имеются и методы объективного определения весов.
для критериев подбираются субъективно, на основе экспертных оценок, однако имеются и методы объективного определения весов.
Основным недостатком аддитивного критерия является возможность компенсации одного критерия за счет других.
Мультипликативное нечеткое множество предпочтительности имеет вид:
 ,
,

Мультипликативные критерии не допускают компенсации, и если значение одного из частных критериев равно нулю, то глобальный критерий также равен нулю.
К достоинствам минимаксного критерия f1 можно отнести также тот факт, что его оптимум не смещается при добавлении новых особей.
Генетический алгоритм с нечёткой моделью
НАЧАЛО
(* формирование начальной популяции решений Р0 ={ai0}, ai=(xi,si) *)
сгенерировать начальную совокупность представлений S0;
сформировать векторы начального множества решений X0=μ-1(S0);
оценить начальные решения Р0: K(S0);
t = 0 (* счетчик итераций *);
(* процедура поиска *)
ПОКА НЕ выполнено условие останова ПОВТОРИТЬ
НАЧАЛО
Rt=Pt
(*репродукционное множество - вся популяция, Np – число особей в популяции*)
ДЛЯ р = 1 до р = Np ПОВТОРИТЬ
НАЧАЛО
(*формирование родительской совокупности*)
выбрать из Rt родительскую совокупность Ррt, состоящую из q особей;
(* кроссовер*)
выбрать число точек кроссовера случайным образом, получить q потомков Орt; оценить новые решения и добавить их в популяцию:
Орt: К(μ (Орt));
Рt=Рt![]() иОрt;
иОрt;
КОНЕЦ
С вероятность Pm для каждого решения акt![]() Рt ПОВТОРИТЬ
Рt ПОВТОРИТЬ
(* Мутация*)
НАЧАЛО
sk = М(акt);
хк = μ-1(sk);
оценить новое решение ак: K(sk);
Рt = Рt![]() аk;
аk;
КОНЕЦ;
(*Приезд иммигрантов*)
сгенерировать совокупность представлений иммигрантов SIt;
сформировать множество решений It= μ-1(Sit);
оценить множество иммигрантов I4: K(Si');
включить иммигрантов в популяцию
Рt = Рt![]() Ipt;
Ipt;
(* Оператор отбора *)
S: Рt![]() Pt+1;
Pt+1;
t = t+1;
КОНЕЦ
КОНЕЦ
Процесс подготовки к оптимизации включает несколько этапов.
1 этап. Определение нечетких переменных.
Для каждого показателя xi, в каком бы месте иерархического дерева он ни находился, определяются три набора оценок:
-оценки уровня качества по этому показателю (нечеткая переменная Уровень, принимающая значения «низкий», «средний», «хороший», «высокий»);
-оценки затрат на достижение качества (нечеткая переменная Стоимость, принимающая значения «низкая», «средняя», «высокая»).
-оценки совокупности стоимости и уровня показателя (нечеткая переменная Качество, принимающая значения «низкое», «среднее», «высокое»).
2 этап. Определение правил вывода.
Далее, для каждого показателя определяются правила нечеткого вывода, имеющие в своей основе базу знаний, формируемую специалистами предметной области в виде совокупности р нечетких предикатных правил вида:
Пj: Если Уровень xi«высок» и Стоимость xi«средняя», то Качество программных средств (ПС) по xi«высокое».
Пр: Если Уровень xi«средний» и Стоимость xi«высокая», то Качество ПС по xi«низкое»
3 этап. Определение переменной Качество.
Определяется правило, по которому все нечеткие множества, назначенные переменной вывода Качество путем применения правил, объединяются в одно нечеткое множество. В данном алгоритме принимается синтез по закону операции max в смысле g1:
![]()
4 этап. Синтез глобального критерия - функции предпочтительности.
Он сводится к синтезу глобального критерия качества ПС
![]()
как функции k исходных критериев, отражающих эффективность системы с точки зрения экономики, технологии, надежности и других. Причем максимум этого критерия будет соответствовать четкому решению многокритериальной задачи.
5 этап. Определение варианта метода приведения к четкости (дефазификация).
Известныпятьвариантовметода (Centroid, First-of-Maxima, Max-Criterion, Height, Middle-of-Maxima). Наиболее предпочтителен метод Middle-of-Maxima, как максимально учитывающий особенности формы получившейся функции принадлежности:

При моделировании сложных систем невозможно учесть воздействие всех реально существующих факторов по причине ограниченности информации об этих факторах и возможностей обработки чрезмерно усложненных моделей.
Поэтому в модель приходится вводить лишь ограниченное число таких факторов, которые по тем или иным соображениям считаются наиболее существенными. Учесть приближенность знаний об этих факторах, а также влияние «несущественных» факторов можно путем введения в математическую модель нечетких критериев, ограничений и предпочтений. Нечеткий характер исходной информации, какими бы факторами он ни был обусловлен, влияет на весь процесс оптимизации, от формирования множества альтернатив и предъявления к ним определенных требований до принятия решения о выборе оптимальной альтернативы.
Основными элементами процесса принятия решения являются:
-пространство альтернатив;
-множество ограничений, которые необходимо учитывать при выборе между различными альтернативами;
-множество критериев, задающих оценку качества альтернативы по тому или иному параметру;
-функция предпочтительности, определяющая упорядочение множества альтернатив в соответствии с предпочтениями субъекта, принимающего решение, и заданная на множестве критериев.
Следует построить такую модель объекта оптимизации, которая бы учитывала нечеткий характер исходной информации при формировании множества альтернатив, критериев и ограничений, а также наличие неопределенностей различной природы в предпочтениях системы принятия решений (СПР). Конструируемая модель должна быть пригодна для описания характеристик ПС и давать возможность использования ГА при поиске приемлемых решений.
Особь в многокритериальном генетическом алгоритме (МКГА) представляет собой нечёткую хромосому - сложную структуру с различными типами полей. Для каждого типа поля может быть определен свой метод мутации. В качестве единого способа предлагается на этапе инициализации алгоритма задавать любым доступным и удобным способом множество возможных вариантов (аллелей) каждого поля (гена), которое затем используется как при формировании начальной популяции, так и при мутагенезе. Фактически, мутация определенного гена особи представляет собой замену его какой-либо случайно выбранной аллелью из множества возможных для данного гена. Применение оператора мутации к популяции после оператора скрещивания регулируется функцией генетического разнообразия (2.6), т.е. добавление аллелей в популяцию может производиться таким образом и до тех пор, пока не установится нужное значение генетического разнообразия.
Формирования репродукционной группы из особей текущей популяции для отбора в следующее поколение производится по одному из следующих вариантов селекционных схем.
Общая схема. Вся популяция, получившаяся в результате применения операторов скрещивания и мутации, считается репродукционной группой;
Элитарная схема. В репродукционную группу включаются все особи предыдущей популяции («родители») и только те «потомки» и «мутанты», чья приспособленность выше, чем хотя бы у одного из «родителей»;
Схема выбора фиксированного числа лучших особей. Популяция упорядочивается по убыванию степеней приспособленности, в репродукционную группу включаются L первых особей;
Схема выбора по средней приспособленности. Подсчитывается средняя приспособленность особей в популяции, в репродукционную группу включаются особи, имеющие приспособленность не ниже средней.
Естественный отбор особей в следующее поколение происходит различными способами. Например, способом пропорциональный отбор. Каждой особи назначается вероятность её отбора ps(хi), равная отношению её приспособленности к суммарной приспособленности популяции:

Простейший пропорциональный отбор - рулетка (roulette-wheel selection) - отбирает особей с помощью v «запусков» рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-oro сектора пропорционален соответствующей величине ps(xi). При таком отборе члены популяции с более высокой приспособленностью будут чаще выбираться, чем особи с низкой приспособленностью.
Установление уровней притязаний в терминах целевых значений и приоритетов часто затруднительно, если это происходит при отсутствии какой-либо информации о характере функции согласования. С другой стороны, точное всеобъемлющее описание согласованной поверхности слишком дорогостоящее, а то и вовсе невозможное занятие, тем более, что Парето-множество может и не быть ограниченным. Интерактивное уточнение предпочтений способствует уменьшению вычислительных затрат путем концентрации оптимизационных усилий на той области, в которой наиболее вероятно нахождение компромиссных решений, и одновременно снабжает лицо, принимающее решение (ЛПР) информацией о функции согласования, которая может быть использована для уточнения предпочтений.
С точки зрения оптимизатора, основная трудность, связанная с последовательным уточнением предпочтений, заключается в том, что изменяется среда, с которой он должен работать, следовательно, на действия ЛПР, возможно, должны быть наложены ограничения, в том смысле, что ЛПР имеет право лишь «сжимать», то есть конкретизировать изначально расплывчатые требования.
Методы преобразования популяции, использующие эвристики
Если ландшафт приспособленности многомодален, то генетический алгоритм (ГА) при поиске оптимума имеет более одного возможного направления эволюции. Хотя изначально популяция имеет достаточный генетический потенциал (разнообразие) для поиска различных локальных оптимумов, при обработке она имеет тенденцию «увлекаться» каким-либо одним из них, несмотря на существование других, не менее достойных. Это явление известно под названием «генетический дрейф» и наблюдается достаточно часто в процессах эволюции, происходящих как в природной, так и в искусственной среде.
Когда все особи считаются одинаково хорошо приспособленными, генетический дрейф может привести к тому, что популяция сойдется только к одной небольшой области согласованной поверхности, если не будут приняты специальные меры, чтобы избежать этого.
Методы, использующие так называемые «ниши», позволяют одновременно искать несколько оптимумов путем поддержания популяционного разнообразия. При формировании ниш, особи, входящие в них, стремятся распределиться вокруг лучших оптимумов.
Разделение приспособленности моделирует конкуренцию особей с целью захвата ограниченных ресурсов в замкнутой системе.
Особи, подобные друг другу, в соответствии с некоторой мерой подобия, взаимно понижают приспособленность друг друга, конкурируя за обладание одними и теми же ресурсами. Та особь, которая изначально имела меньшую приспособленность, но была изолирована от других, имеет большие шансы на воспроизводство, поощряя таким образом генетическое разнообразие (диверсификацию).
Добиться достаточно хорошего описания функции согласования означает найти такой способ выборки точек согласованной поверхности, который позволял бы выбирать точки, находящиеся в разнообразных частях пространства критериальных функций. Предлагается схема разделения приспособленности, при которой размеры «ниши» σразд вычисляются с использованием расстояния между особями в пространстве критериев, при этом в вычислении участвуют только особи, которые имеют одинаковый ранг. Параметр σразд определяет, на каком расстоянии особи способны понижать приспособленность друг друга. Разделение приспособленности оказывает на популяцию давление отбора дополнительно к тому, которое создается при ранжировании, и таким образом противодействует генетическому дрейфу.
Ограничение скрещивания есть попытка учесть тот факт, что особи, слишком сильно отличающиеся друг от друга, в общем, менее подходят для произведения конкурентоспособного потомка, чем те особи, которые подобны другу, поэтому поощряется скрещивание похожих особей. В частности, результат скрещивания отдаленных членов Парето-множества может рассматриваться как нежизнеспособное потомство. Ограничение скрещивания может быть осуществлено тем же способом, что и разделение приспособленности, т.е. путем определения, какова должна быть степень подобия особей для того, чтобы они имели право войти в «родительскую» совокупность.
Оператор скрещивания при формировании «потомков» не влияет на генетическую информацию, содержащуюся в «родительской» совокупности, а дальнейший процесс отбора лишь меняет частоту появления конкретного гена популяции. При этом у некоторых генов эта частота «падает до нуля», что соответствует его исчезновению и уменьшению генетического разнообразия популяции. Одним из способов поддержания генетического разнообразия является фактор изменчивости (разве фактор может быть способом?), который является источником образования новых фенотипических признаков за счет изменения генотипа особей в результате мутаций, определяемых как изменение генотипа особи в результате появления в популяции новых форм аллелей отдельных генов.
Поскольку в алгоритме не используется представление хромосом в виде бинарных строк, то применение единообразного механизма «точечных мутаций», то есть изменения значений отдельных битов на противоположное, не представляется возможным.
Заключение
Рассмотренная в работе генетическая модель АИС и многокритериальные алгоритмы оптимизации реализованы в виде квазигенетического алгоритма. Приведенные методы и алгоритмы применены коллективом разработчиков АИС без использования в явном виде программныхкомплексов эволюционного моделирования при проектировании большой сложной распределённой автоматизированной системы – АИС «Снабжение».
Литература
1. Лужбинин А.В., Лисов О.И. Гомеостаз в управлении качеством электронных телекоммуникационных систем // Научная сессия МИФИ- 2003 : сб. науч. тр. М.: МИФИ, 2003. Т. 2. С. 87-89.
2. Норенков И.П. Исследование эффективности генетического метода с фрагментным кроссовером // Информационные технологии. 2008. № 6. С. 26-29.
3. Норенков И.П. Автоматизированные информационные системы: учеб. пособие. М.: МГТУ, 2011. - 342 с. - (Информатика в техническом университете).
4. Душутин И.В. Оптимизация сложных информационных систем с помощью мультихромосомных генетических алгоритмов: труды Всероссийской межвузовской научно-технической конференции студентов и аспирантов «Микроэлектроника и информатика-97». М.: МИЭТ, 1997. Ч. 2.
5. Борисенко М.Л. Использование нечеткой модели процесса оценивания качества для получения достоверной экспертной оценки // Оборонный комплекс–научно-техническому прогрессу России. 1999. №2. С. 14-18.
6. Лисов О.И., Марков А.Б. Мультихромосомная генетическая модель автоматизированных информационных систем // Открытое образование. 2011. № 2. С. 197-199.
7. Зимнович Р. В., Лисов О. И., Марков А. Б. Управление состоянием распределенных технических систем // Оборонный комплекс - научно-техническому прогрессу России. 2006. № 2. С. 66-70.
Публикации с ключевыми словами: эволюционное моделирование, генетический алгоритм, нечёткие оценки, преобразования популяции, управление качеством АИС
Публикации со словами: эволюционное моделирование, генетический алгоритм, нечёткие оценки, преобразования популяции, управление качеством АИС
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||







