научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0367620
УДК 621.396.96
Россия, МГТУ им. Н.Э. Баумана
Введение
В последние годы возрос интерес к использованию в ближней локации (БЛ) пассивных акустических информационных систем (ИС), осуществляющих обнаружение, распознавание и пеленгацию аэродинамических и наземных объектов.
Отличительная особенность данных ИС – автономность, высокое быстродействие, работа в условиях интенсивных искусственных и естественных помех при большом динамическом диапазоне параметров и нестационарности входных воздействий, работа в условиях реверберационных явлений с узко- и широкополосными сигналами, инвариантность к неинформативным параметрам условий встречи объектов и условий применения, непараметричность, робастность и возможность адаптации, более высокий коэффициент полезного действия по сравнению с активными акустическими системами.
Актуальной является задача обоснования алгоритмов обработки сигналов в пассивных акустических ИС БЛ, осуществляющих классификацию типов объектов по их акустическим излучениям, и улучшение их рабочих характеристик. В акустических ИС БЛ информативные параметры случайных сигналов на входе и помех [1] являются нецентрированными случайными величинами или процессами на ограниченном интервале наблюдения, для которых априорно не известны математические ожидания, оценить которые по нестационарной реализации также не представляется возможным.
В этих условиях невозможно применить традиционные методы статистических решений, требующие вычисления и обработки центрированных параметров сигналов, которые при неизвестных математических ожиданиях получить принципиально невозможно.
Научная новизна
В статье для решения поставленной задачи обоснованы робастные нейросетевые алгоритмы формирования областей принятия решений, использующие априорную информацию о начальных статистических характеристиках акустических сигналов аэродинамических и наземных объектов.
Такие алгоритмы обработки сигналов могут быть использованы для построения новых классов акустических ИС БЛ.
Постановка задачи
Снять ограничения, связанные с нестационарностью информативных параметров, позволяет переход в признаковое пространство, в котором каждая выборочная реализация отображается вектором, а ансамбль реализаций – областью. Для обработки информации в многомерном признаковом пространстве, при отмеченных выше особенностях АИС в ближней локации, необходимы эффективные методы выделения информативных признаков, обоснования решающих функций (разделяющих границ) в условиях априорной неопределенности в сложной помеховой обстановке. Важное значение в этих условиях играет сокращение времени на разработку систем и автоматизация процесса исследования.
Всем отмеченным выше требованиям удовлетворяет подход к созданию принципиально новых ИС БЛ, основанный на обработке в трактах ИС нецентрированных параметров сигналов и помех, на использовании в качестве априорной информации начальных моментов случайных процессов и на применении нейросетевых технологий для исследования и проектирования ИС нового поколения.
В [1, 2]обоснованы информативные признаки акустических сигналов от аэродинамических и наземных объектов военной техники.
Анализировались следующие признаки сигнала:
– длительности интервалов между нулями;
– отсчеты огибающей;
– распределение длительностей интервалов между нулями (гистограммная оценка);
– отсчеты оценок СПМ.
Выбор информативных признаков сигналов самолета и вертолета производился на основе двух методов:
- метода коэффициентов множественной начальной регрессии (КМНР) ,
- дискриминантного анализа.
Таким образом, дискриминантный анализ и метод на основе КМНР показали, что наилучшим признаком в точки зрения разделимости классов следует признать отсчеты оценок спектров сигналов, соответствующие локальным экстремумам спектра, для других сигналов наилучшим признаком в точки зрения разделимости классов следует считать гистограмму распределения интервалов между нулями входных реализаций сигналов.
Рассматривались два метода сокращения размерности входных векторов, основанные на методе главных компонент и на методе КМНР. Обе метода сокращения размерности дают идентичные результаты. В методе главных компонент элементы входного вектора упорядочиваются по убыванию их дисперсий (собственных чисел ковариационной матрицы). Отбрасываются те элементы входного вектора, вклад которых в суммарную дисперсию минимален. Аналогичным образом в методе, использующем КМНР, элементы входного вектора упорядочиваются по убыванию значений средних квадратов ошибки множественных начальных регрессионных представлений. Отбрасываются те элементы входного вектора, для которых эта величина, соответствующая вкладу в регрессионное представление, минимальна.
При использовании метода множественных коэффициентов начальной регрессии (МКНР) признаки не центрировались, в классических методах использовались центрированные признаки.
В условиях плохой обусловленности данных и априорной неопределенности, при неизвестных математических ожиданиях, применение классических методов анализа затрудняется. В этих условиях для анализа разделимости классов эффективнее использовать МКНР, так как данная методика оперирует начальными моментами случайных величин и не требует знания математических ожиданий. Кроме того, использование КМНР связано с меньшими вычислительными затратами при плохой обусловленности данных.
Результаты исследования подтвердили хорошую разделимость классов объектов в пространстве нецентрированных параметров.
Это позволяет сделать вывод о том, что для решения поставленных задач можно использовать нецентрированные параметры анализируемых признаков.
В [1] показано, что для распознавания (классификации) сигналов в качестве информативного признака целесообразно использовать гистограммы распределений длительностей интервалов (РДИН) между нулями входных реализаций.
Как следует из [3],распределение длительностей интервалов между нулями в реализации (РДИН) позволяет судить о спектральном составе сигнала, в [1,2] сделан вывод о достаточной информативности такой характеристики, при этом существенно снижается размерность входного сигнала.
Обоснование нейросетевого алгоритма
Вектор Х РДИН формируется в соответствии с алгоритмом:
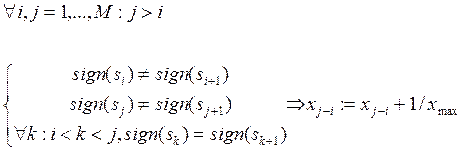 ,
,
где: М ‑ количество отсчетов принимаемого сигнала на интервале времени наблюдения
xmax ‑ константа нормирования РДИН, выбирается на этапе обучения НС.
Суть вектора РДИН ‑ гистограмма распределения количества отсчетов тактовой частоты (в рассматриваемой задаче ft=8192 Гц) в течение одной полуволны сигнала. Точное количество Nх компонент вектора РДИН определяется по результатам обучения нейронной сети. В работе в качестве начального значения выбрано Nх=32. На этапе синтеза нейросетевой системы распознавания (классификации) (НСР) для каждой реализации формируется вектор РДИН.
Спектры выборочных реализаций акустических сигналов самолета, вертолета и фонового шума приведены на рис. 1. Нормированные гистограммы РДИН выборочных реализаций акустических сигналов длительностью 1 сек. самолета, вертолета и танка, после фильтрации при помощи фильтра высокой частоты 3-го порядка с частотой среза 250 Гц приведены на рисунке 2 .

а)

б)

в)
Рисунок 1 – Модифицированная оценка СПМ (периодограмма Уэлча) акустического сигнала самолета (а), вертолета (б) и фонового шума (в)
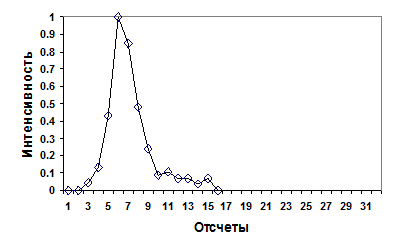
а)

б)

в)
Рисунок 2– Нормированные гистограммы РДИН выборочных реализаций акустических сигналов самолета (а), вертолета (б) и танка (в)
Создание нейросетевой системы распознавания предусматривает разработку программы эмуляции работы нейронной сети и аппаратную реализацию разработанного нейросетевого алгоритма. Количество нейронов и межнейронных связей в сети определяет сложность реализации системы. В работе в качестве базовой выбрана разомкнутая нейронная сеть (НС) с фиксированной структурой, которая предполагала неизменное в режиме настройки число слоев и число нейронов в каждом слое.
В рассматриваемом примере не предполагалось использование НС с перекрестными связями, а анализировалась однородная структура многослойных НС с последовательными связями, которая в простейшем случае реализует кусочно-линейную разделяющую поверхность в исходном пространстве признаков.
Использование последовательных связей позволяет строить безынерционные нейронные сети с простой топологией связей и реализовать произвольное преобразование входного вектора. В работе [3]показано, что трехслойная нейронная сеть с последовательными связями способна реализовать произвольную область принятия решения.
На основании результатов работ по построению аналогичных НС [2] в качестве исходной для исследований выбрана НС с количеством слоев, равным 3. В третьем, выходном слое НС, осуществляется выбор максимального отклика с выходов нейронов второго слоя. выдающего решения о распознаваемых объектах. На каждом к–ом выходе второго слоя НС отклик на входной вектор ![]() , размерностью Nj может быть представлен в виде
, размерностью Nj может быть представлен в виде
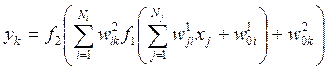 ,
,
где Ni – количество нейронов в первом слое; f1 и f2 – функции активации нейронов соответственно первого и второго слоев ; ![]() – весовые коэффициенты первого слоя;
– весовые коэффициенты первого слоя; ![]() – весовые коэффициенты второго слоя;
– весовые коэффициенты второго слоя; ![]() и
и ![]() – нулевые веса соответственно нейронов первого и второго слоев.
– нулевые веса соответственно нейронов первого и второго слоев.
Выходной слой НС должен состоять из нейронов по количеству распознаваемых классов объектов
При решении задачи рассматривались активационные функции:
– сигмоидальная, или логистическая
 ;
;
– пороговая
 ;
;
– ступенчатая
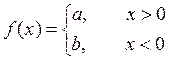 .
.
При обучении НС пороговая и ступенчатая функции активации аппроксимировались дифференцируемыми функциями. При решении задачи обучения НС предполагалось, что учитель точно знает тип объекта для каждой реализации.
Вычислительный эксперимент
Вычислительный эксперимент проводился на ПК типа IntelL(R) Core™ DuoCPUE7300@2,66GГц, 3,25 ОЗУ. Так как решается новая задача, то воспользоваться специальными пакетами программ обучения НС не представляется возможным. Поэтому программное обеспечение разработано специально для решения поставленной задачи выделения нецентрированных информативных признаков и обучения НС, в том числе и робастного.
Обучение нейронной сети производилось на обучающем множестве из 150 реализаций (по 50 для каждого из классов), полученных в результате на основании модельных сигналов. Тестирование НС производилось на тестовом множествах, включающих по 25 реализаций для каждого класса объектов, полученных экспериментально в натурных условиях. В соответствии с выбранным функционалом оптимизации – минимум среднего значения квадрата ошибки между реальным и требуемым значениями выходного сигнала, в качестве алгоритма обучения выбран алгоритм back-propagation [4].
В результате обучения и частичной оптимизации была получена НС с числом нейронов промежуточного слоя N=4. Число нейронов во входном слое сведено к Nx=32. Проводились экспериментальные исследования на 150 имеющихся в распоряжении реализациях и вычисление относительных частот правильной классификации объектов (самолет, вертолет, танк). Относительные частоты правильной классификации объектов составили 95-97 %. Для обеспечения работоспособности нейросетевой системы в условиях неизвестных помех использовано робастное обучение, которое применительно к нецентрированным признакам в БЛ отличается от часто применяемого при обучении НС.
Действительно, если вектор входной реализации обучающего множества U, в общем случае нецентрированный, описывается многомерной плотностью распределения вероятностей ![]() . Неопределенность в исходном описании входного вектора U можно учесть суммированием вектора U с некоррелированным центрированным вектором
. Неопределенность в исходном описании входного вектора U можно учесть суммированием вектора U с некоррелированным центрированным вектором ![]() , обладающим наименее благоприятной для решения поставленной задачи плотностью распределения вероятностей
, обладающим наименее благоприятной для решения поставленной задачи плотностью распределения вероятностей ![]() .Тогда робастное обучение нейросети необходимо проводить, используя новый обучающий вектор Z = U +
.Тогда робастное обучение нейросети необходимо проводить, используя новый обучающий вектор Z = U + ![]() .
.
Как отмечалось выше, вектор входной реализации обучающего множества часто нецентрированый, для которого априорно не известно математическое ожидание. В [2] показано, что в этом случае при формировании обучающего множества для робастного обучения нейросети целесообразно выбирать одинаковую относительную степень различия ![]() по каждой координате
по каждой координате
![]()
где: ![]() - среднее значение квадрата случайной величины
- среднее значение квадрата случайной величины ![]() ;
;
![]() - дисперсия случайной величины Ui.
- дисперсия случайной величины Ui.
При таком задании степени неопределенности наихудшим распределением случайной величины ξi при робастном обучении, как показано в [2], является нормальное.
Тестирование робастно обученных нейронных сетей проводилось на тестовом множестве, сформированном по размытым шумом входным векторам РДИН. В качестве добавляемого к реализациям РДИН использовался некоррелированный шум с гауссовским распределением и диапазоном изменения относительной величины среднего квадратического значения от 0 до 1
Результаты тестирования нейронных сетей с различными количеством нейронов в первом слое и активационными функциями в зависимости от относительного уровня среднего квадратического значения подмешиваемого шума приведены в [1].
Эти зависимости получены путем усреднения результатов экспериментов (проводилось по 10 тестирований для каждого типа НС).
В качестве примера, на рис. 3 приведены зависимости ошибки тестирования робастно обученной нейросети от дисперсии подмешиваемого к реализациям шума для различного количества нейронов во входном слое.
Для оценки влияния изменения весовых коэффициентов на величину дисперсии ошибки откликов нейронной сети была построена зависимость средней ошибки тестирования от величины относительного изменения весовых коэффициентов, приведенная на рис.4. Для её построения использовалось тестирование обученной нейронной сети в пакете прикладных программ Brainmaker, поскольку в нем есть встроенный случайный генератор, имитирующий случайное изменение весов в заданном диапазоне.

а)

б)
Рисунок 3 – Ошибка тестирования робастной НС с логистической (а) и пороговой (б) активационными функциями

Рисунок 4 – Зависимость ошибки тестирования НС от изменения весовых
Заключение
В статье проанализированы информативные признаки акустических сигналов в пассивных акустических ИС БЛ, осуществляющих классификацию типов объектов по их акустическим излучениям. В качестве информативного признака выбрано распределение интервалов между нулями во входной реализации, обоснованы робастные нейросетевые алгоритмы формирования областей принятия решений, использующие априорную информацию о начальных статистических характеристиках акустических сигналов аэродинамических и наземных объектов. Исследованы характеристики синтезированных НС. Показана возможность решения поставленной задачи.
Результаты исследований получены в процессе выполнения проекта П1268 от 09.06.2010 в рамках мероприятия 1.3.1 федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы.
Литература
1. Хохлов В.К., Гулин Ю.Ю. Выбор информативных признаков в автономных информационных системах с нейросетевыми трактами обработки сигналов.–М.: Вестник МГТУ им. Н.Э.Баумана. Сер. «Приборостроение». – 2003. – № 3. – с. 70-83.
2. Хохлов В.К. Обнаружение, распознавание и пеленгация объектов в ближней локации: Учеб. пособие.– М.-: Изд-во МГТУ им. Н.Э. Баумана,2005. – 336 с.
3. Галушкин А.И. Синтез многослойных систем распознавания образов.– М.: Энергия, 1974.– 274 с.
4. Оссовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. - М.: Финансы и статистика, 2002. – 344 с.
Публикации с ключевыми словами: классификация, распознавание, робастный нейросетевой алгоритм, информативные признаки, распределение интервалов между нулями
Публикации со словами: классификация, распознавание, робастный нейросетевой алгоритм, информативные признаки, распределение интервалов между нулями
Смотри также:
- Адаптация нейросетевой системы распознавания вертолета по его акустическому излучению к скорости полета
- Адаптация нейросетевого алгоритма к скоростям движения классифицируемых по акустическим излучениям объектов
- Определение марки автомобиля по видеокадру с использованием модифицированного алгоритма Виолы-Джонса.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



