научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0364256
УДК 537.523+535.23
Россия, МГТУ им. Н.Э. Баумана
Неравновесные селективно излучающие разряды, к которым относятся, например, разряды низкого давления в смеси паров ртути с инертным газом, являются объектом многочисленных фундаментальных и прикладных исследований. Библиография по физике данных разрядов весьма обширна и отражена, в частности, в монографиях [1-4]. Существующие теории основываются на ряде допущений, связанных с приближенным рассмотрением радиационных процессов (метод эффективного времени жизни с постоянным по радиусу коэффициентом поглощения), использованием усредненных по радиусу величин (концентраций и температур электронов и тяжелых частиц), упрощением схемы переходов между уровнями атомов, введением различных аппроксимаций для сечений упругих и неупругих столкновений частиц компонент и т.д. В настоящей работе строится вычислительная модель разряда, свободная от большинства указанных допущений и более реалистично учитывающая истинную картину процессов в плазме с сильной неравновесностью. Модель реализована в соответствующем программном обеспечении.
Модель разряда формулируется в гидродинамическом приближении [5]. В качестве различных сортов частиц рассматриваются электроны, ионы, атомы плазмообразующей компоненты в основном «0» и различных возбужденных «n» состояниях с объемными концентрациями ![]() и
и ![]() , а также частицы буферного газа. Кинетическая часть модели строится на основе индивидуального учета группы низко расположенных уровней излучающих атомов с детальным рассмотрением столкновительных и радиационных механизмов их заселения и опустошения, и объединения большого числа уровней, примыкающих к континууму, в квазинепрерывный спектр со свободными электронами. В этом спектре переходы описываются моделью диффузии электронов в пространстве энергии [6]. Скорости неупругих процессов возбуждения
, а также частицы буферного газа. Кинетическая часть модели строится на основе индивидуального учета группы низко расположенных уровней излучающих атомов с детальным рассмотрением столкновительных и радиационных механизмов их заселения и опустошения, и объединения большого числа уровней, примыкающих к континууму, в квазинепрерывный спектр со свободными электронами. В этом спектре переходы описываются моделью диффузии электронов в пространстве энергии [6]. Скорости неупругих процессов возбуждения![]() и ионизации
и ионизации ![]() атомов при соударениях с электронами и обратных им процессов
атомов при соударениях с электронами и обратных им процессов ![]() рассчитываются с помощью функции распределения электронов по энергиям, которая находится из уравнения Больцмана [5]. В нем в качестве параметров фигурируют температура
рассчитываются с помощью функции распределения электронов по энергиям, которая находится из уравнения Больцмана [5]. В нем в качестве параметров фигурируют температура ![]() и концентрация
и концентрация ![]() электронов, а также заселенности основного
электронов, а также заселенности основного ![]() и резонансного
и резонансного ![]() уровней излучающих атомов. Перенос излучения рассматривается в нескольких оптически плотных резонансных линиях с фойхтовским контуром, уширенных доплеровским, штарковским, резонансным и вандерваальсовским механизмами. Остальные линии учитываются в приближении объемного высвечивания.
уровней излучающих атомов. Перенос излучения рассматривается в нескольких оптически плотных резонансных линиях с фойхтовским контуром, уширенных доплеровским, штарковским, резонансным и вандерваальсовским механизмами. Остальные линии учитываются в приближении объемного высвечивания.
Вычислительная модель включает уравнения энергии для электронов и тяжелых частиц (атомов и ионов) с температурами ![]() и
и ![]() , непрерывности и движения для заряженных частиц и возбужденных атомов и переноса излучения. В уравнении энергии для электронов учитываются неупругие потери на излучение и возбуждение частиц
, непрерывности и движения для заряженных частиц и возбужденных атомов и переноса излучения. В уравнении энергии для электронов учитываются неупругие потери на излучение и возбуждение частиц
![]()
![]()
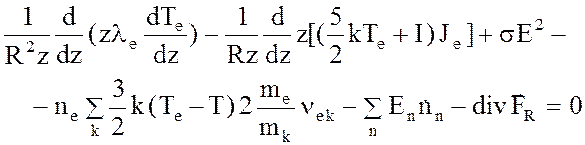 .
.
Уравнения непрерывности для возбужденных частиц, в которых учтено радиационное заселение из основного состояния, относятся к типу Бибермана- Холстейна
 .
.
Система дополняется граничными условиями и рядом соотношений, отражающих протекание процессов в замкнутом объеме, и решается численными методами. В уравнениях обозначено:![]() - безразмерная радиальная координата в цилиндре радиуса R,
- безразмерная радиальная координата в цилиндре радиуса R, ![]() - радиальный поток атомов, находящихся на уровне n,
- радиальный поток атомов, находящихся на уровне n, ![]() - коэффициенты теплопроводности электронов и электропроводности плазмы,
- коэффициенты теплопроводности электронов и электропроводности плазмы, ![]() - энергии возбуждения уровня nи ионизации атома,
- энергии возбуждения уровня nи ионизации атома,![]() - вероятность спонтанного распада уровня,
- вероятность спонтанного распада уровня, ![]() - интегральный по спектру радиальный поток излучения,
- интегральный по спектру радиальный поток излучения, ![]() - спектральные коэффициент поглощения и объемная плотность излучения в резонансной линии на частоте
- спектральные коэффициент поглощения и объемная плотность излучения в резонансной линии на частоте ![]() , c- скорость света,
, c- скорость света, ![]() - частота упругих столкновений электронов с тяжелыми частицами.
- частота упругих столкновений электронов с тяжелыми частицами.
Количество входных параметров модели ограничено: давления (масса) компонент, диаметр разрядной трубки, температура стенки, электрический ток. Применение описанной модели требует обширной базы данных по характеристикам элементарных процессов в плазме, включая многочисленные сечения упругих и неупругих столкновений, сечения фотоионизации, вероятности спонтанных радиационных переходов, параметры уширения линий. Эти данные частично заимствуются из различных источников или рассчитываются согласно [7, 8].
Ниже приведены некоторые результаты моделирования ртутных стационарных разрядов низкого давления с аргоновым буфером. В модели учитывались эффекты, связанные с изотопным составом природной ртути [2].
В области энергий электронов до порога возбуждения атома ртути на уровни ![]() (около 4.7 эВ) функция распределения электронов по энергиям мало отличается от максвелловской в силу доминирующего значения межэлектронных столкновений. В запороговом диапазоне возрастает роль неупругих процессов, и отличие функции распределения от максвелловской становится заметным (как в [2]).
(около 4.7 эВ) функция распределения электронов по энергиям мало отличается от максвелловской в силу доминирующего значения межэлектронных столкновений. В запороговом диапазоне возрастает роль неупругих процессов, и отличие функции распределения от максвелловской становится заметным (как в [2]).
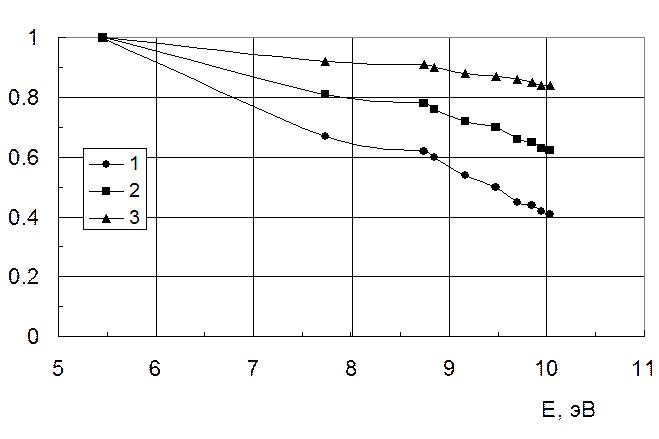
Рис. 1. Отношение скоростей возбуждения электронным ударом различных уровней Hg из состояния ![]() , рассчитанных при истинной и максвелловской функциях распределения электронов, в зависимости от энергии возбуждаемых уровней.
, рассчитанных при истинной и максвелловской функциях распределения электронов, в зависимости от энергии возбуждаемых уровней.
![]() ,
,![]() ,заселенность резонансного уровня равна 0.3 от больцмановской.
,заселенность резонансного уровня равна 0.3 от больцмановской.
1 –3 - ![]() , соответственно. Маркеры на кривых соответствуют следующим уровням в порядке увеличения их энергий:
, соответственно. Маркеры на кривых соответствуют следующим уровням в порядке увеличения их энергий:
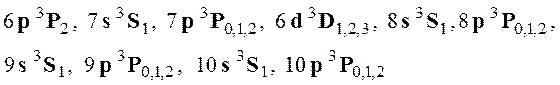 .
.
Из рис.1 следует, что уровень ![]() , ближайший к уровню
, ближайший к уровню![]() (пороговая энергия равна 0.57 эВ), возбуждается в основном максвелловскими электронами. Для уровня
(пороговая энергия равна 0.57 эВ), возбуждается в основном максвелловскими электронами. Для уровня ![]() (порог 2.84 эВ) скорость возбуждения составляет уже 0.7-0.92 от равновесной, а для уровня
(порог 2.84 эВ) скорость возбуждения составляет уже 0.7-0.92 от равновесной, а для уровня ![]() (порог 5.14 эВ) - 0.4 – 0.8. Видно, что степень влияния фактора неравновесности функции распределения на скорости возбуждения и ионизации зависит от порога процесса. Сопоставление данных теории и эксперимента проведено на рис. 2, 3. Нарастание температуры электронов к стенке связано с поглощением излучения, выходящего из центральных зон разряда с повышенной концентрацией излучающих частиц.
(порог 5.14 эВ) - 0.4 – 0.8. Видно, что степень влияния фактора неравновесности функции распределения на скорости возбуждения и ионизации зависит от порога процесса. Сопоставление данных теории и эксперимента проведено на рис. 2, 3. Нарастание температуры электронов к стенке связано с поглощением излучения, выходящего из центральных зон разряда с повышенной концентрацией излучающих частиц.

Рис. 2. Распределение температур электронов (1,3) и тяжелых частиц (2) в разряде.
1,2-настоящая работа, R=19 мм, ток равен 0.42 A, давление Hg и Ar 0.85 и 465 Па; 3-данные эксперимента[4], R=18 мм, ток равен 0.4 А, давление Hg и Ar 0.85 и 390 Па.
Перепад температуры тяжелых частиц между стенкой и центром не превышает 70К, температура тяжелых частиц во много раз отличается от температуры электронов (рис.2). Тонкой физической и важнейшей эксплуатационной характеристикой разрядов является поток излучения в резонансных линиях (рис.3). В рассмотренных условиях в линии 253.7 нм излучается от 50 до 70% подводимой электрической мощности. С ростом электрического тока мощность излучения нарастает линейно, а затем имеется тенденция к насыщению из-за возрастающей роли тушащих электронных ударов.

Рис. 3. Зависимость потока излучения в линии 253.7 нм от электрической мощности. Давление Hg 0.85 Па. 1-данные эксперимента [4], R=18 мм, давление Ar 390 Па; 2- результаты настоящей работы, R=19 мм, давление Ar 465 Па.
Предложенная теоретическая модель удовлетворительно (в пределах 15 %) согласуются с результатами экспериментов по всем основным параметрам разрядов (сравнение проводилось также с данными других авторов, например, [2, 3, 9]) и открывает новые возможности в исследовании физических эффектов в плазме и разработке перспективных источников селективного излучения.
СПИСОК ЛИТЕРАТУРЫ
1. Грановский В.Л. Электрический ток в газе. Установившийся ток. – М.: Наука, 1971.- 543 с.
2. Миленин В.М., Тимофеев Н.А. Плазма газоразрядных источников света низкого давления. - Л.: Изд-во Ленинтрад. ун-та, 1991 – 239 с.
3. Рохлин Г.Н. Разрядные источники света. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1991.- 720 с.
4. Уэймаус Д. Газоразрядные лампы / Пер. с англ.; Под ред. Г.Н. Рохлина и М.И. Фугенфирова. - М.: Энергия, 1977. – 367 с.
5. Митчнер М., Кругер Ч. Частично ионизованные газы / Пер. с англ.; Под ред. А.А. Иванова. - М.: Мир, 1976. – 496 с. (Mitchner M., Kruger Ch. Partially Ionized Gases. Department of mechanical engineering Stanford university. New York London Sydney Toronto, 1973).
6. Биберман Л.М., Воробьев В.С., Якубов И.Т. Кинетика неравновесной низкотемпературной плазмы. – М.: Наука, 1982. – 375 с.
7. Sinyarev G.B., Gradov V.M. Complex Calculations of High Pressure Discharge Irradiation Characteristics // Beitrage aus der Plasmaphysik. - 1984. - Bd.24, №5. -p.499 – 528
8. Gradov V.M., Gavrish S.V. Mathematical modeling of selective emitting nonequilibrium plasma in complex optical systems // Light & Engineering.–1997. - v.5, №3.- p.16-19.
9. Kreher J., Stern W. Contrib. Increased Power Concentration and its Effects on the Discharge Parameters of the Low Pressure Hg-rare Gas Positive Column. II. Variation of Tube Radius // Plasma Phys. - 1989.- v.29, №2. - p.181-196.
Публикации с ключевыми словами: разряд, вычислительная модель, неравновесная плазма
Публикации со словами: разряд, вычислительная модель, неравновесная плазма
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



