научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2012
DOI: 10.7463/0512.0356070
УДК 62-137
Россия, МГТУ им. Н.Э. Баумана
Для существенного уменьшения количества модельных и натурных испытаний геометрия проточных частей насосов уточняется численным экспериментом в программном пакете STARCCM+ 6.04. Для использования результатов компьютерного моделирования численная модель должна быть верифицирована физическим экспериментом. Для этих целей на кафедре “Гидромеханика, гидромашины и гидропневмоавтоматика” МГТУ им. Н.Э. Баумана в рамках проекта "Разработка и производство отечественных насосных агрегатов нового класса для транспорта нефти (импортозамещающие технологии)" при финансовой поддержке Министерства образования и науки РФ (Постановление Правительства РФ № 218) проводились испытания проточных частей насосов НМ на уменьшенным моделях, а также проводилось их численное моделирование.
Была составлена численная модель проточной части модели насоса по исходной 3D-геометрии, использованной при изготовлении проточной части на 3D принтере.

Рисунок 1 - 3D-геометрия проточной части модели насоса НМ2500-230
Метод численного моделирования основан на решении дискретных аналогов базовых уравнений гидродинамики. В случае модели несжимаемой жидкости (ρ=const) это:
Уравнение сохранения массы (уравнение неразрывности)
![]() ,
,
Уравнение сохранения количества движения (уравнение Навье-Стокса)
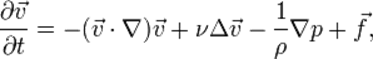
В прямой постановке для решения полноразмерной трехмерной задачи турбулентного течения в насосе необходимо использовать очень мелкую расчетную сетку, размер ячеек которой настольно мал, что современные вычислительные ресурсы не позволяют разрешить задачу. Поэтому при данном расчете использовались уравнения Навье-Стокса, осредненные по Рейнольдсу, и дополнительные два дифференциальных уравнения, отвечающие за моделирование турбулентности.
В данной задаче использовалась модель k-ω SST модель турбулентности. Пограничный слой описывался пристеночными функциями.
Использовалась структурированная призматическая расчетная сетка в 10 слоев вблизи твердых стенок и неструктурированная многогранная в ядре потока.
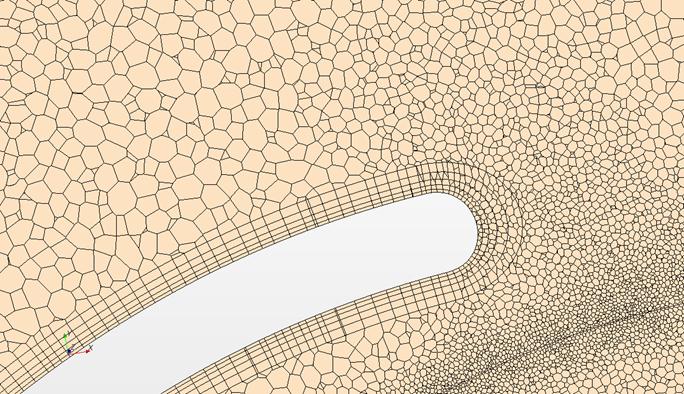
Рисунок 2 - Структурированная сетка в пристенной области

Рисунок 3 - Расчетная сетка для модели насоса НМ2500-230
Вращение рабочего колеса моделировалось как в стационарной, так и в нестационарной постановке. Т.е. предварительный расчет проводился на неподвижной сетке, а эффект вращения моделировался добавлением силовых факторов воздействующих на жидкость во вращающейся области (т.е. силы инерции и кориолисовы силы). После стационарного расчета он использовался как начальное условие для решения нестационарной задачи и расчета динамических эффектов.
Граничные условия, используемые при расчете: поток массы на входе и давление на выходе.
Первым этапом, как численного моделирования, так и натурного эксперимента являлось снятие интегральных характеристик агрегата, а именно построение напорной и энергетических характеристик агрегата.
Для сравнения с численным экспериментом были взяты результаты испытаний модели насоса при частоте вращения 2000 об/мин.
Характеристики, полученные при натурных испытаниях при номинальной частоте вращения 2000 об/мин, представлены в графическом виде.

Рисунок 4 - Характеристика модели насоса НМ2500-230 при частоте вращения 2000 об/мин
Расчет проводился для тех же значений расхода, что и полученные в ходе эксперимента.
В результате стационарного расчета при частоте вращения 1970 об/мин и подаче 33 л/с (первая точка была выбрана как точка с наивысшим значением КПД, т.е. оптимальная) была получена картина течения внутри насоса.
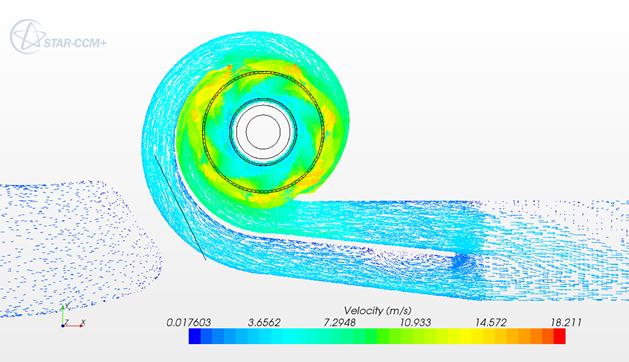
Рисунок 5 - Векторное поле скоростей в сечении насоса при подаче 33 л/с (сечение перпендикулярное оси вращения)
Рисунок 6 - Векторное поле скоростей внутри рабочего колеса (сечение перпендикулярное оси вращения)
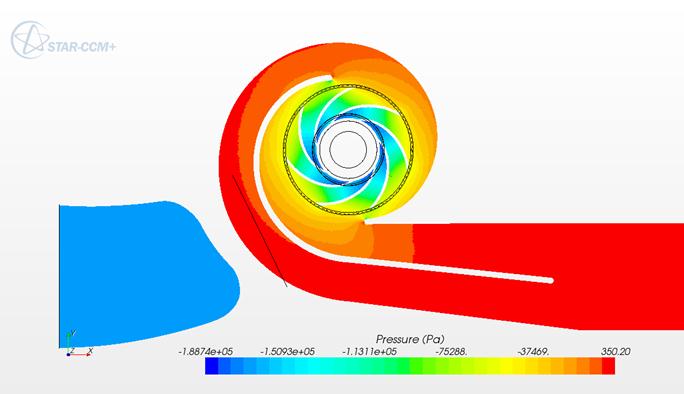
Рисунок 7 - Поле давлений в сечении насоса (сечение перпендикулярное оси вращения)
Значения интегральных параметров, полученных в результате расчета, следующие:
Сравнение результатов расчета и эксперимента в номинальной точке
| Н, м | М, Нм | КПД, % |
Эксперимент | 14,65 | 32,2 | 71,7 |
Расчет | 15,7 | 30,94 | 79 |
Погрешность, % | 7,1 | 3,9 | 10,1 |
Значения расчетных параметров отличаются от экспериментальных данных на величину погрешности. Этому есть две причины:
1. Погрешность численного эксперимента, связанная с дискретизацией исходных непрерывных уравнений гидродинамики и применение моделей турбулентности, которые являются упрощённым представлением реальных гидродинамических процессов. С этой погрешностью трудно бороться, так как ее уменьшение требует значительного увеличения вычислительных ресурсов и экономически не обосновано. Более того погрешность носит систематический характер и может быть учтена применением поправочных коэффициентов.
2. Погрешность, связанная с неполным учётом в модели факторов, присутствующих в физическом эксперименте, в частности, таких как механические потери мощности на валу насоса, утечки жидкости по щелевым уплотнениям и пр. Для устранения данной погрешности необходимо было дополнительное проведение балансовых испытаний.
При проведении балансовых испытаний были определены значения внешнего механического КПД и объёмного КПД. Внешний момент трения составил 2,5 Нм. Значение объемного КПД составило 0,97.
Таким образом, к расчетному моменту следует прибавить значение указанного момента трения, а расчетный напор скорректировать с учетом увеличенного расхода через рабочее колесо на значение перетечек в щелевых уплотнениях.
Ниже приведены некоторые результаты численного моделирования течения на других режимах по подаче (Рисунок 8, Рисунок 9, Рисунок 10).
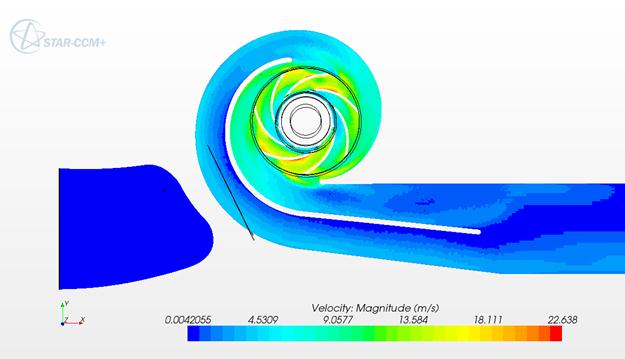
Рисунок 8 - Распределение модуля скорости в сечении насоса при подаче 11 л/с (сечение перпендикулярное оси вращения)
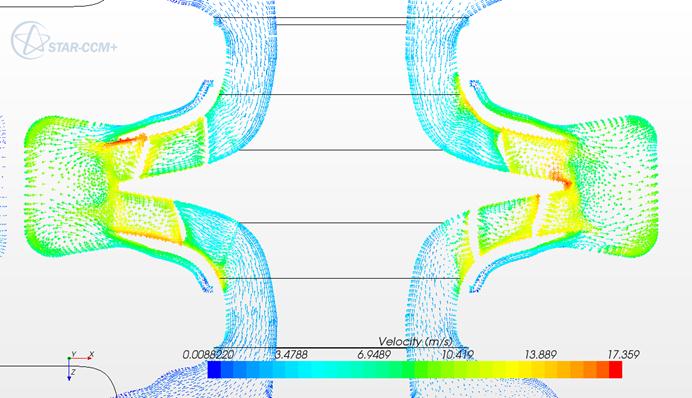
Рисунок 9 - Распределение векторов скорости в сечении насоса при подаче 11 л/с (сечение по плоскости разъема насоса)

Рисунок 10 - Распределение модуля скорости в сечении насоса при подаче 21 л/с (сечение перпендикулярное оси вращения)

Рисунок 11 Распределение модуля скорости в сечении отвода при подаче 44 л/с
Сравнение расчетных и экспериментальных характеристик представлено в табличном и графическом виде:
Таблица 2
Сравнение скорректированного расчетного и измеренного момента на валу насоса
Подача Q, л/с | Расчетный скорректированный момент М, Нм | Экспериментально измеренный момент, Нм | Погрешность, % |
0 | 15,5 | 16,5 | 6,06 |
6 | 18,93 | 20,8 | 8,99 |
11 | 23 | 22,8 | 0,88 |
16 | 24,51 | 25,2 | 2,74 |
23 | 28,7 | 28,4 | 1,06 |
28 | 31,15 | 30,8 | 1,14 |
33 | 33,44 | 32,2 | 3,85 |
39 | 34,63 | 33,3 | 3,99 |
44 | 35,76 | 33,5 | 6,75 |
49 | 34,92 | 33 | 5,82 |
53 | 33,8 | 31,5 | 7,30 |
Таблица 3
Сравнение скорректированного расчетного и измеренного напора насоса
Подача Q, л/с | Расчетный скорректированный напор Н, м | Экспериментально измеренный напор Н, м | Погрешность, % |
0 | 19,00 | 17,7 | 7,34 |
6 | 19,27 | 18 | 7,08 |
11 | 19,37 | 17,8 | 8,84 |
16 | 18,98 | 17,95 | 5,76 |
23 | 18,65 | 17,35 | 7,49 |
28 | 17,47 | 16,25 | 7,52 |
33 | 15,50 | 14,65 | 5,81 |
39 | 14,10 | 12,9 | 9,31 |
44 | 12,11 | 10,45 | 15,9 |
49 | 9,25 | 7,6 | 21,7 |
53 | 6,63 | 3,65 | 81,7 |
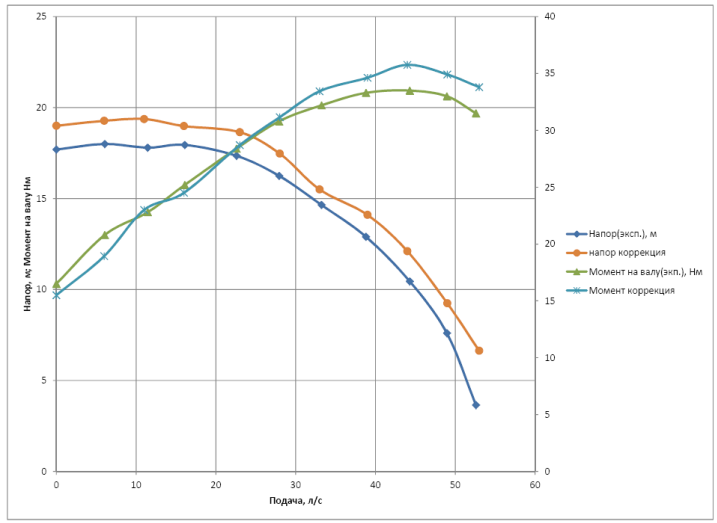
Рисунок 12 Сравнение результатов испытаний и скорректированного расчета
Из графика видно, что погрешность расчета напора носит систематический характер (за исключением области наибольших подач насоса) и в дальнейшем может быть учтена поправочным коэффициентом. Причины появления данной систематической погрешности могут быть выявлены в ходе дальнейших испытаний и моделирования. Погрешность вычисления момента ниже, а на каких-то режимах практически отсутствует.
Список использованной литературы
1. CD-adapco STAR CCM UserGuide 6.02. США 2011. URL: http://158.110.32.35/download/SCD/star_uguide.pdf. (Дата обращения 19.03.2012)
2. ГОСТ 6134-2007 Насосы динамические. Методы испытаний. М: 2007. 91 с.
Публикации с ключевыми словами: верификация, численное моделирование, нефтяной насос
Публикации со словами: верификация, численное моделирование, нефтяной насос
Смотри также:
- Экспериментальная верификация данных численного эксперимента на основе дифференциального метода применительно к центробежному насосу двухстороннего входа
- Экспериментальное исследование истечения жидкости через насадки и сравнение с результатами гидродинамического моделирования
- Потери кинетической энергии и КПД осевой турбиной ступени при моделировании нестационарных течений
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



