научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК.536.42
МГТУ им. Н.Э. Баумана
Будущее топливно-энергетического комплекса России связано с освоением нефтегазовых ресурсов арктических шельфов. Задачи, связанные с изучением, прогнозом и управлением температурными полями в грунтовых средах, в настоящее время являются одними из наиболее важных и востребованных в сфере инженерной геологии и строительства. В современных условиях, когда на территории Российской Федерации происходит разработка новых месторождений нефти и газа, все чаще поднимается проблема строительства в районах вечной мерзлоты, ведь они занимают 64 % от площади РФ и 25 % площади всего мира. В их строении выделяются ярусы охлажденных ниже 0°С и многолетнемерзлых пород. Составление прогноза изменений температурного режима грунтов является необходимым элементом инженерно-геологического обоснования строительства (реконструкции, расширения) объектов нефтегазовой промышленности в районах распространения вечномерзлых грунтов. Целью данной работы является построение математической модели, позволяющей составлять подобные температурные прогнозы. Эта модель должна учитывать фазовые переходыв трехмерной области.
Прогноз изменений температурного режима грунтов может выполняться приближенными аналитическими методами, с помощью моделирования, а также численными методами. Задача определения температурного поля в процессе термостатирования многофазных веществ является нелинейной и относится к классу задач со свободной границей, в которых часть границы не задана и должна быть определена вместе с решением системы дифференциальных уравнений теплопроводности.
Научная новизна работы заключается в следующем. С помощью интегро-интерполяционного метода (метода контрольных объемов) была получена дискретная постановка задачи Стефана, сводящаяся к задаче нахождения решения системы линейных алгебраических уравнений с трехдиагональной матрицей. Решение такой системы было получено с помощью метода прогонки (для одномерного случая) и метода переменных направлений (для двух- и трехмерного случаев). Задача была приведена к безразмерному виду.
Температурный режим (совокупность последовательных температурных полей в грунтовом массиве, соответствующих любым заданным моментам времени от начала расчета) рассчитывается как результат задаваемых на весь период расчета прогноза тепловых воздействий на верхней, боковых и нижней границах грунтового массива.
Расчетный алгоритм составлен и может быть применен для расчетных областей, ограниченных прямоугольной верхней границей, в контурах которой фиксированы тепловыделяющие объекты. В трехмерном случае область исследования параллелепипед, в двухмерном — прямоугольник и в одномерном — прямая.
В разработанном алгоритме учитываются условия на границе слоев, условия на границе фазового перехода воды в лед, физические свойства грунтов: суглинок буро-коричневый, супесь буровато-коричневая с прослоями суглинка и песка, песок пылеватый. Теплофизические характеристики корректируются по ходу вычислений при изменении влажности и температуры. Величина солнечной радиации определяется в зависимости от месяца и географической широты.
Численная реализация выполнена на языке Fortran. Программа способна рассчитать температурное поле в заданной области исследования при наличии определенного набора входных данных: физические характеристики области исследования, геометрическое разбиение области исследования, начальное распределение температуры, граничные условия.
Следует отметить, что большая часть работ, связанных с температурными полями в таких средах носит экспериментальный характер, поэтому численное моделирование прогноза физических характеристик является особенно актуальным. Предшествующие работы посвящены решению подобных задач в двумерных и одномерных областях, либо построению моделей трехмерных моделей без учета фазовых переходов. Автором была рассмотрена подобная задача в энтальпийной постановке, с которой можно ознакомиться в [1]. Разработанная модель может найти применение в таких отраслях как строительство в зоне вечной мерзлоты, геология, космонавтика и др.
1 Теплопроводность твердых тел
Процесс теплообмена представляет собой перенос энергии, происходящий между телами (средами), имеющими различную температуру. Тепловое поле на данный момент времени tопределяется распределением температуры по телу, т.е. функцией ![]() , где
, где ![]() — декартовы координаты. В простейшем случае тепловой поток направлен из области с более высокой температурой в область с более низкой температурой.
— декартовы координаты. В простейшем случае тепловой поток направлен из области с более высокой температурой в область с более низкой температурой.
Основное положение теории теплопроводности, известное как закон Фурье, состоит в предположении пропорциональности теплового потока градиенту температуры в однородной среде: ![]() , где
, где ![]() – коэффициент теплопроводности. Для получения уравнения переноса тепла запишем закон сохранения энергии в виде
– коэффициент теплопроводности. Для получения уравнения переноса тепла запишем закон сохранения энергии в виде
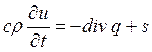 , (1.1)
, (1.1)
где sопределяет мощность внутренних источников теплоты, с – удельная теплоемкость, ![]() - плотность среды.
- плотность среды.
Подстановка выражения для потока в (1.1) позволяет записать основное дифференциальное уравнение теплопроводности
 . (1.2)
. (1.2)
Коэффициенты и правая часть уравнения могут зависеть как от точки пространства (при неоднородной среде), так и от температуры.
Если теплофизические свойства среды постоянные (однородная среда), то уравнение теплопроводности (1.2) упрощается и принимает вид
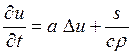 ,
,
где 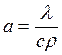 - коэффициент температуропроводности,
- коэффициент температуропроводности, ![]() - оператор Лапласа.
- оператор Лапласа.
Другой частный случай уравнения теплопроводности (1.2) соответствует описанию установившихся тепловых полей. Стационарное уравнение теплопроводности имеет вид ![]() и является эллиптическим уравнением второго порядка.
и является эллиптическим уравнением второго порядка.
При моделировании теплопереноса в движущейся среде (движущейся системе координат) уравнение теплопроводности (1.2) соответствующим образом трансформируется. Переход основан на замене частной производной по времени ![]() на полную производную по времени (субстанциональную производную)
на полную производную по времени (субстанциональную производную)  , где
, где ![]() - локальная скорость среды. Поэтому уравнение теплопроводности в движущейся среде записывается в виде
- локальная скорость среды. Поэтому уравнение теплопроводности в движущейся среде записывается в виде
 . (1.3)
. (1.3)
Здесь член с ![]() определяет изменение температуры за счет конвективного переноса.
определяет изменение температуры за счет конвективного переноса.
Распределение температуры в точках среды в различные моменты времени определяется из уравнения теплопроводности. Для однозначного определения температуры поля помимо уравнения необходимо сформулировать дополнительные (замыкающие) соотношения, так как решения уравнений в частных производных определяются с точностью до некоторых произвольных функций.
Для этого дифференциальное уравнение в общем виде дополняется: уравнениями состояния, уравнениями неразрывности, условиями в начальный момент времени, условиями на границах тела, данными о геометрии (в частности, условиями симметрии), о теплофизических свойствах материала, а иногда и другими замыкающими задачу сведениями.
Отдельно рассмотрим условия на границе контакта двух сред с различными теплофизическими характеристиками. Прежде всего, остановимся на вопросе, какие условия сопряжения естественны для уравнения теплопроводности, и, следовательно, их можно явно не формулировать. В этом случае условия контакта обуславливаются только разрывами теплофизических характеристик при переходе границы сред.
Будем считать, что контакт двух однородных сред проходит по плоскости ![]() . Теплофизические характеристики, отнесенные к среде, занимающей полупространство
. Теплофизические характеристики, отнесенные к среде, занимающей полупространство ![]() , будем помечать плюсом, а для второй среды (когда
, будем помечать плюсом, а для второй среды (когда ![]() ) будем использовать обозначения с минусом. Рассмотрим уравнение теплопроводности в виде
) будем использовать обозначения с минусом. Рассмотрим уравнение теплопроводности в виде
 , (1.7)
, (1.7)
причем коэффициенты разрывны при ![]() :
:
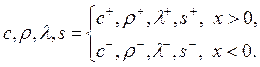 (1.8)
(1.8)
С учетом такого разрыва коэффициентов уравнения (1.7) естественно считать, что само решение уравнения (температура u) непрерывно, а вот его первые производные уже разрывны. Поэтому напишем условие непрерывности температуры при переходе из одной среды в другую в форме
![]() ,
, ![]() , (1.9)
, (1.9)
где через [ ] обозначен скачок при переходе границы контакта. В рассматриваемом случае ![]() . Осталось сформулировать условия сопряжения для первых производных температуры.
. Осталось сформулировать условия сопряжения для первых производных температуры.
Для того, чтобы получить естественные условия сопряжения для уравнения теплопроводности (1.7) с разрывными коэффициентами (1.8), можно поступить следующим образом. Выделим на границе контакта некоторую ограниченную область ![]() и проинтегрируем исходное уравнение теплопроводности (1.7) по области шириной
и проинтегрируем исходное уравнение теплопроводности (1.7) по области шириной ![]()
![]() .
.
С учетом непрерывности температуры (условие (1.9)), конечности разрывов при ![]() получим
получим
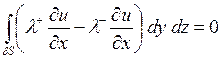 .
.
В силу произвольности выбора элемента ![]() получим условие сопряжения в виде
получим условие сопряжения в виде
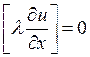 ,
, ![]() . (1.10)
. (1.10)
Условие сопряжения (1.10) отражает непрерывность теплового потока.
Естественные условия сопряжения записываются аналогично (1.9), (1.10) на произвольной криволинейной границе сопряжения двух сред ![]() внутренней границе области
внутренней границе области ![]() . Они отражают непрерывность температуры и теплового потока и записываются в виде
. Они отражают непрерывность температуры и теплового потока и записываются в виде
![]() ,
, ![]() , (1.11)
, (1.11)
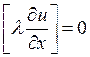 ,
, ![]() . (1.12)
. (1.12)
Уравнение (1.11) характеризует условие непрерывности температурного поля, а уравнение (1.12) ‑ закон сохранения энергии на поверхности соприкасающихся тел при условии идеального теплового контакта. Подчеркнем еще раз, что условия (1.11) и (1.12) являются естественными для уравнения (1.7) с разрывными коэффициентами (1.8), они включены в само уравнение и нет необходимости каждый раз формулировать их отдельно.
Если на границе двух сред не выполнены условия идеального контакта (непрерывности температуры и теплового потока), то необходимо специально формулировать условия сопряжения, которые дополняют уравнение теплопроводности, записанное в каждой отдельной среде. Эти условия сопряжения отражают особенности тепловых процессов на границе контакта, особенности поведения решения задачи при переходе границы контакта и не всегда могут включаться в само уравнение теплопроводности.
Пусть на границе контакта имеется поверхностный тепловой источник мощности ![]() . Тогда справедливо предположение о непрерывности температуры, т. е. выполнено условие (1.11), а вот тепловой поток претерпевает разрыв. Вместо однородного условия сопряжения (1.12) необходимо записать неоднородное условие сопряжения вида
. Тогда справедливо предположение о непрерывности температуры, т. е. выполнено условие (1.11), а вот тепловой поток претерпевает разрыв. Вместо однородного условия сопряжения (1.12) необходимо записать неоднородное условие сопряжения вида
 ,
, ![]() . (1.13)
. (1.13)
Условия сопряжения могут включаться в само уравнение теплопроводности, которое записывается для всей расчетной области без выделения границы контакта ![]() . Поверхностный источник тепла учитывается дополнительным слагаемым в уравнении (1.7)
. Поверхностный источник тепла учитывается дополнительным слагаемым в уравнении (1.7)
 , (1.14)
, (1.14)
где ![]() есть поверхностная
есть поверхностная ![]() -функция, определяемая так, что для любой функции
-функция, определяемая так, что для любой функции ![]() справедливо соотношение
справедливо соотношение
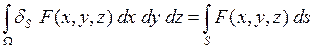 .
.
В вычислительной теплофизике выделяют и другие типы условий сопряжения. В качестве примера отметим условия типа сосредоточенной теплоемкости, когда также имеет место непрерывность температуры, а разрыв теплового потока определяется соотношением
 ,
, ![]() , (1.15)
, (1.15)
где ![]() — сосредоточенная теплоемкость контакта. Условия сопряжения (1.11), (1.15) с использованием поверхностной
— сосредоточенная теплоемкость контакта. Условия сопряжения (1.11), (1.15) с использованием поверхностной ![]() -функции включаются в уравнение теплопроводности подобно уравнению (1.14).
-функции включаются в уравнение теплопроводности подобно уравнению (1.14).
В прикладных исследованиях большого внимания заслуживают условия неидеального контакта. Такой случай реализуется, например, при недостаточно плотном соприкосновении шероховатых твердых тел. При неидеальном контакте тепловой поток непрерывен, что является отражением закона сохранения энергии. Таким образом, одно условие сопряжения мы имеем — условие (1.12). Температура при переходе границы неидеального контакта терпит разрыв, пропорциональный тепловому потоку
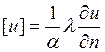 ,
, ![]() .
.
Здесь коэффициент контактного теплообмена ![]() связан с условиями контакта.
связан с условиями контакта.
2 Математическая постановка задачи
В классической задаче Стефана рассматриваются фазовые превращения с участием твердой фазы — твердое тело—жидкость. Примером таких превращений являются процессы затвердевания и плавления в металлургии. Соответствующие математические модели характеризуются наличием подвижных заранее неизвестных границ фазового перехода — задач со свободными (неизвестными) границами.
Основная предпосылка при моделировании фазовых превращений твердое тело—жидкость состоит в том, что фазовый переход происходит при заданной постоянной температуре фазового перехода u*. Пусть фазовый переход происходит на границе раздела фаз, которую мы обозначим S, причем S=S(t). Эта граница разделяет расчетную область ![]() на две подобласти. Область
на две подобласти. Область ![]() , занятая жидкой фазой, где температура превышает температуру фазового перехода, есть
, занятая жидкой фазой, где температура превышает температуру фазового перехода, есть ![]() . Соответственно, область
. Соответственно, область ![]() , занятая твердой фазой,
, занятая твердой фазой, ![]() . Аналогичные обозначения используем и для теплофизических величин в каждой отдельной фазе.
. Аналогичные обозначения используем и для теплофизических величин в каждой отдельной фазе.
Выпишем соответствующие уравнения теплопроводности. В твердой фазе имеем
 ,
, ![]() , (2.1)
, (2.1)
где ![]() . Учитывая конвективный перенос в жидкой фазе, получим
. Учитывая конвективный перенос в жидкой фазе, получим
 ,
, ![]() , (2.2)
, (2.2)
где ![]() .
.
Нас интересуют условия на границе фазового перехода ![]() . Прежде всего на этой границе контакта двух сред справедливы предположения о непрерывности температуры (1.11), т. е.
. Прежде всего на этой границе контакта двух сред справедливы предположения о непрерывности температуры (1.11), т. е.
![]() ,
, ![]() . (2.3)
. (2.3)
Фазовый переход сопровождается выделением/поглощением определенного количества тепла. Поэтому тепловой поток на границе фазового перехода разрывен и определяется величиной
 ,
, ![]() , (2.4)
, (2.4)
где ![]() - теплота фазового перехода, а
- теплота фазового перехода, а ![]() - скорость движения границы фазового перехода по нормали.
- скорость движения границы фазового перехода по нормали.
Как мы уже выше отмечали, предполагается, что фазовый переход происходит при постоянной температуре ![]() . Поэтому сама граница фазового перехода
. Поэтому сама граница фазового перехода ![]() определяется на каждый момент времени следующим образом:
определяется на каждый момент времени следующим образом: ![]() или, в другой форме, на границе фазового перехода выполнены условия первого рода
или, в другой форме, на границе фазового перехода выполнены условия первого рода
![]() ,
, ![]() . (2.5)
. (2.5)
Условия (2.3)-(2.5) есть условия Стефана, а соответствующая задача для уравнений (2.1), (2.2) называют задачей Стефана. Рассматриваемая задача характеризуется тем, что исследуются процессы в обеих фазах, поэтому в этом случае говорят о двухфазной задаче Стефана. Предельная ситуация характеризуется тем, что тепловое поле в одной из фаз известно (температура равна температуре фазового перехода). Поэтому рассматривается тепловое поле только для одной из фаз — однофазная задача Стефана [6]. В этом случае неизвестная граница фазового перехода ![]() является не внутренней, а внешней.
является не внутренней, а внешней.
Например, будем считать, что область ![]() занята твердой фазой при температуре
занята твердой фазой при температуре ![]() . Тогда для нахождения температуры в жидкой фазе используется уравнение (2.2) в переменной области
. Тогда для нахождения температуры в жидкой фазе используется уравнение (2.2) в переменной области ![]() со следующими условиями на
со следующими условиями на ![]() :
:
![]() ,
, ![]() . (2.6)
. (2.6)
 ,
, ![]() . (2.7)
. (2.7)
Условия типа (2.6), (2.7) характеризуют однофазную задачу Стефана.
С точки зрения построения эффективных вычислительных алгоритмов чрезвычайно важное значение имеет тот факт, что задача Стефана допускает обобщенную формулировку, при которой условия (2.3)-(2.5) включаются в само уравнение теплопроводности. Включение неоднородных условий сопряжения на заданной границе раздела в само уравнение обсуждалось выше. В задаче Стефана ситуация осложняется тем, что граница раздела фаз ![]() сама неизвестна, и ее нужно найти.
сама неизвестна, и ее нужно найти.
Поясним переход от уравнений (2.1), (2.2) с условиями (2.3)-(2.5) к одному уравнению теплопроводности. В соответствии с (2.4) и (1.13)-(1.14) уравнения (2.1), (2.2) можно записать в виде одного уравнения
 ,
, ![]() . (2.8)
. (2.8)
Вблизи границы фазового фронта введем локальную ортогональную координатную систему ![]() , метрические коэффициенты которой равны единице, В этих новых координатах поверхностная
, метрические коэффициенты которой равны единице, В этих новых координатах поверхностная ![]() -функция
-функция ![]() есть
есть ![]() , где уравнение
, где уравнение ![]() определяет границу
определяет границу ![]() . Аналогично для скорости движения свободной границы имеем
. Аналогично для скорости движения свободной границы имеем ![]() . Условие Стефана (2.6) соответствует тому, что в новых координатах
. Условие Стефана (2.6) соответствует тому, что в новых координатах ![]() ,
, ![]() . С учетом этого получим
. С учетом этого получим
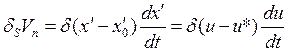 . (2.9)
. (2.9)
Подстановка (2.9) в (2.8) дает уравнение
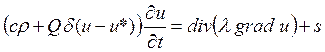 ,
, ![]() , (2.10)
, (2.10)
Уравнение (2.9) примечательно тем, что в него не входит явно сама неизвестная граница фазового перехода. Фронт фазового перехода в такой постановке задачи находится как изотермическая поверхность ![]() , положение которой в пространстве, а в общем случае и форма, изменяются с течением времени. Учет теплоты фазового перехода эквивалентен заданию эффективной теплоемкости:
, положение которой в пространстве, а в общем случае и форма, изменяются с течением времени. Учет теплоты фазового перехода эквивалентен заданию эффективной теплоемкости: ![]() .
.
Квазилинейное уравнение теплопроводности (2.10) лежит в основе эффективных процедур приближенного решения задач Стефана. Нелинейности в этой задаче изменяют не только количественный характер тепловых процессов, но и качественную картину их протекания. Они значительно усложняют математические модели тепловых процессов, причем во многом эти трудности связаны с невозможностью применения для нелинейных задач принципа суперпозиции решений.
В общем виде (2.10) такая задача не имеет полного аналитического решения. Однако найдены точные аналитические решения для некоторых частных случаев (например, для постоянных коэффициентов и для коэффициентов, зависящих только от температуры). Подробнее с ними можно ознакомиться в [3-4, 7-11].
Требуется найти распределение температуры в среде с фазовыми переходами твердое тело ‑ жидкость. Тепловое состояние такой среды с учетом теплоты фазового перехода описывается уравнением теплопроводности вида
 (3.1)
(3.1)
где ![]() – удельная теплоемкость;
– удельная теплоемкость; ![]() – плотность;
– плотность; ![]() – коэффициент теплопроводности;
– коэффициент теплопроводности; ![]() – температура среды;
– температура среды; ![]() – температура фазового перехода;
– температура фазового перехода; ![]() – теплота фазового перехода;
– теплота фазового перехода; ![]() – мощность внутренних источников тепла;
– мощность внутренних источников тепла; ![]() – дельта-функция.
– дельта-функция.
Решение ![]() требуется найти в ограниченной области (рис. 1) – прямоугольном параллелепипеде
требуется найти в ограниченной области (рис. 1) – прямоугольном параллелепипеде ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() . На границе
. На границе ![]() с температурой происходит конвективный теплообмен со средой, имеющей температуру
с температурой происходит конвективный теплообмен со средой, имеющей температуру ![]() . Плотность теплового потока на этой границе задается через коэффициент теплоотдачи
. Плотность теплового потока на этой границе задается через коэффициент теплоотдачи ![]() в виде
в виде
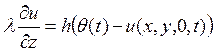 .
.

Рис. 1. Расчетная область
Коэффициент теплоотдачи ![]() записывается в виде
записывается в виде ![]() , где
, где ![]() ‑ коэффициент конвективного теплообмена и R ‑ коэффициент термического сопротивления.
‑ коэффициент конвективного теплообмена и R ‑ коэффициент термического сопротивления.
На границе ![]() поддерживается постоянный тепловой поток (поток из недр Земли согласно [12])
поддерживается постоянный тепловой поток (поток из недр Земли согласно [12])
 .
.
Боковые границы области ![]() теплоизолированы:
теплоизолированы:
 ,
, 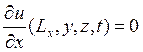 ,
,
 ,
, 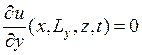 .
.
В качестве примера расчета рассматривается задача о распределении температурных полей в грунте в районах с сезонными промерзаниями и оттаиваниями почвы (аналогично РСН 67-87 ([29]) и [30]). Рассмотрим здание со свайным фундаментом и термостабилизаторами. Такой тип фундамента часто встречается при строительстве в зоне вечномерзлых грунтов. Предположим, что сверху на грунте построено здание. Необходимо найти распределение температурных полей под зданием, чтобы узнать глубину оттаивания грунтов под ним. Если под зданием через некоторый промежуток времени будут скапливаться оттаявшие грунты, здание может осесть в котлован, образовывающийся под тяжестью самого здания, а затем и вовсе разрушиться [31].
Термостабилизатор – это парожидкостное устройство для охлаждения грунтов, представляющее собой металлическую герметично запаянную, заправленную хладагентом трубку диаметром от 36 до 57 мм, длиной от 6 до 10 м и более, состоящее из конденсатора с оребрением (надземной части длиной в пределах 1—2,5 м) и испарителя (подземной части длиной от 5 до 9 м и более). Работа осуществляется без внешних источников питания, только за счет законов физики — переноса тепла вследствие испарения в испарителе хладагента и его поднятия в конденсаторную часть, где пар конденсируется, отдавая тепло, и стекает по внутренним стенкам трубы вниз. В качестве хладагента применяется экологически безвредный, не воспламеняющийся и взрывобезопасный фреон R22. В расчетах будем использовать гладкостенные термостабилизаторы СОУ СГВ-100-40/9 с глубиной погружения в грунт ![]() , общей длиной 9 м и мощностью
, общей длиной 9 м и мощностью  [32, 35]. Термостабилизатор работает с 1 октября по 31 марта и не работает с 1 апреля по 30 сентября каждого каждого года. Термостабилизатор рассматривается как бесконечно тонкий стержень:
[32, 35]. Термостабилизатор работает с 1 октября по 31 марта и не работает с 1 апреля по 30 сентября каждого каждого года. Термостабилизатор рассматривается как бесконечно тонкий стержень:
![]() .
.
В задаче мы будем рассматривать самый простой тип термостабилизаторов: прямой, без изменения формы для теплоотвода. У здания нет вентилируемого подполья, поэтому термостабилизаторы находятся вне границы здания.
Пусть область исследования ![]() имеет вид, представленный на рис. 2. Плоскость
имеет вид, представленный на рис. 2. Плоскость ![]() соответствует поверхности земли. Ось
соответствует поверхности земли. Ось ![]() направлена вглубь грунта. Закрашенный прямоугольник на верхней границе области соответствует четверти здания, расположенному над этой областью. Размер этого прямоугольника (горизонтального сечения здания) составляет
направлена вглубь грунта. Закрашенный прямоугольник на верхней границе области соответствует четверти здания, расположенному над этой областью. Размер этого прямоугольника (горизонтального сечения здания) составляет ![]() (рис. 3.1). Характеристики области
(рис. 3.1). Характеристики области ![]() :
: ![]() =21 м,
=21 м, ![]() =15 м,
=15 м, ![]() =17 м. Область
=17 м. Область ![]() состоит из 3 литологических слоев:
состоит из 3 литологических слоев:![]() ,
, ![]() и
и ![]() (соответственно, области 1, 2 и 3 на рисунке 1). Эти множества задаются следующим образом:
(соответственно, области 1, 2 и 3 на рисунке 1). Эти множества задаются следующим образом:
![]() ;
;
![]() ;
;
![]() .
.
Область исследования ![]() содержит 6 свай и 5 термостабилизаторов, расположенных как показано на рис. 2.
содержит 6 свай и 5 термостабилизаторов, расположенных как показано на рис. 2.

Рис. 2. Верхняя граница расчетной области
В зоне 2 (на рис. 2 – это заполненный текстурой «кирпичная стена» прямоугольник) располагается производственное здание, физические характеристики в этой зоне остаются постоянными во времени. Условия в зонах 1 и 3 изменяются по интервалам времени – месяцам года (см. таблицу 1). За начало отсчета принимается 01 января текущего года. Через год эти условия повторяются, т.е. условия на верхней границе являются периодическими функциями времени с периодом ![]() (1 год). Боковые границы области теплоизолированы, и условия на них не зависят от времени. Поток на боковых границах в плоскостях
(1 год). Боковые границы области теплоизолированы, и условия на них не зависят от времени. Поток на боковых границах в плоскостях ![]() и
и ![]() считаются равным нулю в силу симметрии (см. п. 3.1.1), а на двух других плоскостях равен нулю, т.к. эти грани удалены достаточно далеко и не оказывают влияния на распределение температурных полей под зданием. Начальное распределение температуры по глубине представлено в таблице 3.3.
считаются равным нулю в силу симметрии (см. п. 3.1.1), а на двух других плоскостях равен нулю, т.к. эти грани удалены достаточно далеко и не оказывают влияния на распределение температурных полей под зданием. Начальное распределение температуры по глубине представлено в таблице 3.3.
Таблица1
Физические характеристики на верхней границе расчетной области
Зоны | Характерис-тика | Месяц | |||||||||||
I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | ||
1 | Температура
| -24,6 | -23,8 | -19,2 | -9,5 | 3,7 | 13,1 | 18,0 | 12,4 | 4,6 | -4,6 | -16,4 | -22,4 |
Термическое сопротивление R, м2·ч·°С/ккал | 2,6 | 2,7 | 2,8 | 3,0 | 1,7 | - | - | - | - | 1,3 | 2,1 | 2,3 | |
Коэффициент конвективного теплообмена | 13,8 | 12,3 | 12,3 | 12,0 | 12,1 | 12,6 | 13,4 | 13,0 | 14,3 | 13,4 | 13,5 | 12,7 | |
2 | Температура
|
| |||||||||||
Термическое сопротивление R, м2·ч·°С/ккал | R=1,8= const | ||||||||||||
Коэффициент конвективного теплообмена |
| ||||||||||||
3 | Температура
| -24,6 | -23,2 | -19,2 | -9,5 | 3,7 | 13,1 | 18,0 | 12,4 | 4,6 | -4,6 | -16,4 | -22,4 |
Термическое сопротивление R, м2·ч·°С/ккал | 4,4 | 4,4 | 4,7 | 5,0 | 2,82 | - | - | - | - | 2,14 | 3,57 | 3,59 | |
Коэффициент конвективного теплообмена | 13,8 | 12,3 | 12,3 | 12,0 | 12,1 | 12,6 | 13,4 | 13,0 | 14,3 | 13,4 | 13,5 | 12,7 | |
Согласно РСН 67-87, СНиП 2.02.04-88, и ГОСТ 25100-82 ([29], [32] и [33] соответственно) можно написать для слагаемого ![]() в левой части уравнения (3.1) выражение
в левой части уравнения (3.1) выражение
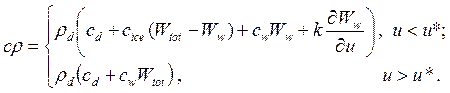 (3.2)
(3.2)
Здесь  — удельная теплоемкость сухого грунта,
— удельная теплоемкость сухого грунта,  ‑ удельная теплоемкость льда,
‑ удельная теплоемкость льда,  – удельная теплоемкость воды,
– удельная теплоемкость воды, ![]() – плотность сухого грунта,
– плотность сухого грунта, ![]() – суммарная влажность грунта в долях к массе сухого грунта,
– суммарная влажность грунта в долях к массе сухого грунта, ![]() – доля незамерзшей воды по отношению к массе сухого грунта,
– доля незамерзшей воды по отношению к массе сухого грунта,  ‑ удельная теплота фазового перехода льда,
‑ удельная теплота фазового перехода льда, ![]() ‑ температура фазового перехода.
‑ температура фазового перехода.
Формула для объемной теплоемкости (3.2) учитывает фазовые переходы в области отрицательных температур. Функцией ![]() описывается массовая доля (по отношению к массе сухого грунта) незамершей воды при температуре
описывается массовая доля (по отношению к массе сухого грунта) незамершей воды при температуре ![]() [29, 34]. Подробнее нахождение этой функции описано ниже.
[29, 34]. Подробнее нахождение этой функции описано ниже.
Коэффициент теплопроводности ![]() в уравнении (3.1) определяется выражением
в уравнении (3.1) определяется выражением
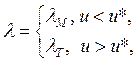 (3.3)
(3.3)
где ![]() – коэффициент теплопроводности мерзлого грунта,
– коэффициент теплопроводности мерзлого грунта, ![]() – коэффициент теплопроводности талого грунта.
– коэффициент теплопроводности талого грунта.
Коэффициент теплоотдачи ![]() записывается в виде
записывается в виде ![]() , где значения коэффициента конвективного теплообмена
, где значения коэффициента конвективного теплообмена ![]() и термического сопротивления
и термического сопротивления ![]() находятся по таблице 1 (см. [29]).
находятся по таблице 1 (см. [29]).
Теплота фазового перехода ![]() принимается равной количеству теплоты, необходимой для таяния льда (замерзания воды) в единице объема грунта и вычисляется по формуле
принимается равной количеству теплоты, необходимой для таяния льда (замерзания воды) в единице объема грунта и вычисляется по формуле ![]() в соответствии со СНиП 2.02.04-88 [32]. Внутренние источники тепла в рассматриваемой задаче отсутствуют, поэтому
в соответствии со СНиП 2.02.04-88 [32]. Внутренние источники тепла в рассматриваемой задаче отсутствуют, поэтому ![]() .
.
Физические характеристики литологических слоев, необходимые для расчета, приведены в таблице 2 (см. РСН 67-87, ГОСТ 25100-82, СП 32-101-95 [29, 33, 35]).
На нижней границе области ![]() (см. рис. 2) зададим поток из недр Земли [12]
(см. рис. 2) зададим поток из недр Земли [12]  .
.
Таблица 2
Физические характеристики литологических слоев
Номер слоя | Характеристика | ||||||
rd, кг/м3 | сd, ккал/(кг·°С) | Wtot, доли | lM, ккал/(м·ч·°С) | lT, ккал/(м·ч·°С) | Ww (u), доли | ||
u,°С | WW (u) | ||||||
1 | 1390 | 0,22 | 0,25 | 1,3 | 1,15 | -0,3 | 0,14 |
-1,0 | 0,12 | ||||||
-10,0 | 0,08 | ||||||
2 | 1520 | 0,24 | 0,22 | 1,55 | 1,55 | -0,3 | 0,12 |
-1,0 | 0,08 | ||||||
-10,0 | 0,05 | ||||||
3 | 1500 | 0,23 | 0,27 | 2,35 | 2,15 | 0 | 0 |
0 | 0 | ||||||
0 | 0 | ||||||
Верхняя граница области ![]() , представленная на рисунке 3.4, разбита на 3 зоны: 1, 2 и 3. Будем рассматривать режим теплообмена на прилегающей территории, наименее благоприятный для эксплуатации здания. Предположим, что снежные надувы образовывались симметрично со всех сторон здания. В результате определялся температурный режим под четвертью частью здания, образованной осями симметрии. В процессе эксплуатации здания с одной из его сторон на части прилегающей территории в зимнее время будут образовываться снежные надувы (увеличение максимальной мощности снега на 0,4 м по сравнению с естественным). Зона снежных надувов обозначена на рис. 2 цифрой 3.
, представленная на рисунке 3.4, разбита на 3 зоны: 1, 2 и 3. Будем рассматривать режим теплообмена на прилегающей территории, наименее благоприятный для эксплуатации здания. Предположим, что снежные надувы образовывались симметрично со всех сторон здания. В результате определялся температурный режим под четвертью частью здания, образованной осями симметрии. В процессе эксплуатации здания с одной из его сторон на части прилегающей территории в зимнее время будут образовываться снежные надувы (увеличение максимальной мощности снега на 0,4 м по сравнению с естественным). Зона снежных надувов обозначена на рис. 2 цифрой 3.
Таблица 3
Начальное распределение температуры по глубине
Глубина, м | 1 | 3 | 5 | 7 | 9,5 | 12,5 | 15,5 |
°С | -0,1 | -0,4 | -1,0 | -1,2 | -1,4 | -1,4 | -1,4 |
Дополнительно к разбиению области расчета на блоки, в каждом блоке по всем трем направлениям ![]() ,
, ![]() и
и ![]() вводилась равномерная сетка: длины блоков по каждому направлению делились на 5 частей. Таким образом, в результате число контрольных объемов по
вводилась равномерная сетка: длины блоков по каждому направлению делились на 5 частей. Таким образом, в результате число контрольных объемов по ![]() ,
, ![]() и
и ![]() составило, соответственно, 40, 30 и 35, т.е. общее число элементов в расчетной области (это же число равняется числу внутренних расчетных точек в области
составило, соответственно, 40, 30 и 35, т.е. общее число элементов в расчетной области (это же число равняется числу внутренних расчетных точек в области ![]() ) равняется
) равняется ![]() . В ходе методических расчетов проводилось сравнение вариантов разбиения каждого блока на 5, 7, 9 и 11 частей. Установлено, что разбиение на 5 частей позволяет с точностью до 10-5 находить распределение температур. Остальные варианты не дают ощутимый выигрыш в точности, в то время как эти варианты существенно снижают время расчетов. Минимальный безразмерный шаг по пространству
. В ходе методических расчетов проводилось сравнение вариантов разбиения каждого блока на 5, 7, 9 и 11 частей. Установлено, что разбиение на 5 частей позволяет с точностью до 10-5 находить распределение температур. Остальные варианты не дают ощутимый выигрыш в точности, в то время как эти варианты существенно снижают время расчетов. Минимальный безразмерный шаг по пространству  ,
,  . В качестве рассматриваемого интервала времени выбран интервал
. В качестве рассматриваемого интервала времени выбран интервал ![]() . Число итераций по времени выбрано равным 6000. Тогда безразмерный шаг по времени
. Число итераций по времени выбрано равным 6000. Тогда безразмерный шаг по времени  . Безразмерная полуширина сглаживания
. Безразмерная полуширина сглаживания ![]() -функции
-функции  . В качестве показателя даты выбран стандартный формат «дд.мм.гг», где годы будет иметь вид 01, 02, 03, 04 или 05.
. В качестве показателя даты выбран стандартный формат «дд.мм.гг», где годы будет иметь вид 01, 02, 03, 04 или 05.
На вертикальных линиях, проходящих параллельно оси ![]() через точки наблюдения M1(1.5,1), M2(9,5) (см. рис. 2), выведены на печать в определенных точках по глубине зависимости температуры
через точки наблюдения M1(1.5,1), M2(9,5) (см. рис. 2), выведены на печать в определенных точках по глубине зависимости температуры ![]() в этих точках от времени
в этих точках от времени ![]() (рисунки 4-5). По графикам наглядно видно, что в точках М1 и М2 термостабилизаторы постепенно снижают температуру.
(рисунки 4-5). По графикам наглядно видно, что в точках М1 и М2 термостабилизаторы постепенно снижают температуру.
Видно, что к концу рассматриваемого периода (5 лет) температура под зданием становится отрицательной уже на глубине порядка 2 м. Это означает, что бόльшая часть грунта находится в твердом состоянии, и зданию не угрожает разрушение. Для свай глубиной залегания 8 м. это вполне допустимая глубина промерзания. Три четверти длины сваи находится в твердом грунте, что позволит зданию устоять без просадки. Хотя следует отметить, что для большей безопасности необходимо использовать термостабилизаторы строго под зданием рядом со сваями. Таким образом, можно подморозить грунт в непосредственной близости от свай и почти полностью сваи будут находиться в твердом грунте. Это особенно важно при строительстве крупных зданий. Также есть смысл строительства зданий с вентилируемым подпольем, за счет чего значительно уменьшится эффект накопления тепла под зданием. В данном случае граничные условия не будут принимать постоянное значение. Однако построение такой модели требует учесть движение воздушных масс и их прогревание, а также их специфический теплообмен с дисперсной средой. По данному направлению ведутся исследования, достигнутые результаты изложены в [37].

Рис. 3. Зависимость температуры от времени в точке М1 на глубинах: 1 – 1 м., 2 – 3 м., 3 – 5 м., 4 – 7 м., 5 – 15,5 м.

Рис. 4. Зависимость температуры от времени в точке М2 на глубинах: 1 – 1 м., 2 – 3 м., 3 – 5 м., 4 – 7 м., 5 – 15,5 м.
В результате выполнения данного проекта была разработана эффективная математическая модель для определения температурных полей в низкотемпературных двухфазных средах. В ходе работы были получены результаты прогноза распределения температурных полей для зданий с разным типом фундамента: свайный, ленточный и без фундамента; рассмотрен вариант охлаждения грунта под зданием с помощью термостабилизаторов.
Кроме того была создана программа, которая реализует численное решение класса трехмерных обобщенных задач Стефана в безразмерном виде. Программа позволяет прогнозировать распределение температурных полей в низкотемпературных двухфазных средах во времени. Разработанная программа может найти применение в таких отраслях промышленности как космонавтика, геология, строительство в зоне вечной мерзлоты и др.
1 Крылов Д.А., Мельникова Ю.С. Математическое моделирование распределения температурных полей в криолитозоне // Студенческий научный вестник. Сборник статей четвертой научно-технической выставки «Политехника». М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. С.94-97.
2 Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Книжный дом «ЛИБРОКОМ», 2009. 784 с.
3 Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
4 Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 599 с.
5 Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х томах. Т.1. ‑ М.: Мир, 1991. ‑ 504 с.
6 Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х томах. Т.2. М.: Мир, 1991. 552 с.
7 Тихонов А.Н., Самарский А.А. Уравнения математической физики: учеб. пособие. М.: Изд-во МГУ, 1999. 799 с.
8 Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики: учебник для студентов вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 1996.
9 Фридман А. Вариационные принципы и задачи со свободными границами. М.: Наука, 1990. 536 с.
10 Власова Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики: учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 704 с.
11 Синай Я.Г. Теория фазовых переходов. Строгие результаты. М.: Наука, 1980. 208 с.
12 Короновский Н.В. Общая геология: учебник. М.: Изд-во «Книжный дом университет», 2006. 528 с.
13 Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1977. 440 с.
14 Зарубин В.С. Математическое моделирование в технике: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. 496 с.
15 Ferziger Joel H., Petric M. Computational methods for fluid dynamics. 3 rev. ed. ‑ New York: Springer, 2002. ‑ 423 p.
16 Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. ‑ М.: Наука, 1989. ‑ 432 с.
17 Галанин М.П., Савенков Е.Б. Методы вычислений. Уравнения в частных производных. Интегральные уравнения: Учеб. пособие. М.: Изд-во ИПМ им. М.В. Келдыша РАН, 2006. 72 с.
18 Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации: Учеб. для вузов. М.: Изд-во МГТУ им. Н. Э. Баумана, 2003. 440 с.
19 Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). Определения, теоремы, формулы. Спб.: Изд-во «Лань», 2003. 832 с.
20 Галанин М.П., Савенков Е.Б. Методы вычислений. Обыкновенные дифференциальные уравнения. Разностные схемы: Учеб. пособие. М.: Изд-во ИПМ им. М.В. Келдыша РАН, 2006. 90 с.
21 Отчет по теме «Фундаментальные основы управления нестационарным температурным режимом в криолитозоне» / МГТУ. Руководитель темы Н.И. Сидняев. ГР № 01201151171, Инв. № 02201157901. М., 2010, 306 с.
22 Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984. 152 с.
23 Патанкар С.В. Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах. М.: Изд-во МЭИ, 2003. 312 с.
24 Веденеева Е.А. Применение метода контрольного объема к решению задач динамики вязких теплопроводных жидкостей. М.: Изд-во МГУ, 2009. 87 с.
25 Сборник задач по методам вычислений: Учеб. пособие для вузов / Под ред. П.И. Монастырского. М.: Физматлит, 1994. 320 с.
26 Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 544 с.
27 Галанин М.П., Савенков Е.Б. Методы вычислений. Алгебра. Интерполяция: Учеб. пособие. М.: Изд-во ИПМ им. М.В. Келдыша РАН, 2006. 80 с.
28РСН 67-87. Инженерные изыскания для строительства. Составление прогноза изменений температурного режима вечномерзлых грунтов численными методами. М., 1987.
30 Крылов Д.А., Сидняев Н.И., Федотов А.А. Математическое моделирование распределения температурных полей в вечномерзлых грунтах // Материалы Международной научно-практической конференции по инженерному мерзлотоведению, посвященной ХХ-летию создания ООО НПО «Фундаментстройаркос»» - Тюмень. Изд-во «Сити-пресс», 2011. С. 126-132.
31 Цытович Н.А. Механика мерзлых грунтов. М.: Высшая школа, 1973. 448 c.
32СНиП 2.02.04-88. Основания и фундаменты на вечномерзлых грунтах. М., 1998.
33ГОСТ 25100-82. Грунты. Классификация. М., 1982.
34 Роман Л.Т. Механика мерзлых грунтов. М.: МИАК «Наука/Интерпериодика», 2002. 426 с.
35СП 32-101-95. Проектирование и устройство фундаментов опор мостов в районах распространения вечномерзлых грунтов. М., 1996.
36 Попов А.П., Милованов В.И. и др. К вопросу о типовых технических решениях по основаниям и фундаментам для криолитозоны // Инженерная геология. 2008. Сентябрь. ‑ С. 22-38.
37. Крылов Д.А., Сидняев Н.И. Метод расчета массовой кристаллизации многофазных реологических сред // Материалы Четвертой конференции геокриологов России. МГУ им. М.В. Ломоносова, 7-9 июня 2011 г. Т. 1. Часть 1. Физико-химия, теплофизика и механика мерзлых пород. М.: Университетская книга, 2011. С. 129-136.
Публикации с ключевыми словами: математическая модель, прогноз, грунт, температурное поле, фазовый переход, термостабилизатор
Публикации со словами: математическая модель, прогноз, грунт, температурное поле, фазовый переход, термостабилизатор
Смотри также:
- 77-30569/330390 Математическое моделирование управления нестационарным температурным полем в двухфазных средах
- 77-30569/252086 Проблемы метрологического обеспечения объектов техносферы, строительной науки и практики
- 77-30569/251611 Анализ геодеформационных проявлений вибросейсмических процессов объектов техносферы
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



