научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК 004.8
МГТУ им. Н.Э. Баумана
Одним из ключевых этапов разработки экспертных систем (ЭС) является этап тестирования (оценки). На данном этапе реализованный прототип ЭС с первично наполненной базой знаний оценивается по ряду показателей качества на основе тестовых примеров и специально подготовленных входных данных [1]. При получении неудовлетворительных значений показателей качества решения экспертной системой, как правило, прибегают к переформулированию правил принятия решения или модификации определений понятий в базе знаний. При реализации ЭС для анализа действий оператора на интерактивном тренажере это приводит к искажению семантического содержания понятий и правил базы знаний, что отрицательно сказывается на адекватности экспертной системы при объяснении получаемых результатов и снижает ее полезность для оператора.
В данной работе рассматривается метод редукции ошибок нечеткого вывода продукционных ЭС, не требующий модификации начальной экспертной базы знаний.
В общем случае процесс тестирования ЭС и редукции ошибок показан на рис. 1. В процессе тренировки, оператор оценивает текущее состояние ![]() имитируемого объекта и принимает решение о воздействии
имитируемого объекта и принимает решение о воздействии ![]() на органы управления тренажера. В случае слабой формализации правил принятия управляющих воздействий и сложности анализа действий оператора ЭС формирует вариант «эталонного» решения
на органы управления тренажера. В случае слабой формализации правил принятия управляющих воздействий и сложности анализа действий оператора ЭС формирует вариант «эталонного» решения ![]() , который определяет основу для оценки действий оператора.
, который определяет основу для оценки действий оператора.

Рис. 1. Редукция ошибок в экспертных системах интерактивных тренажеров
В случае слабой формализации правил принятия решения алгоритм вывода ЭС может допускать неприемлемую погрешность решения в частных случаях исходных данных, то есть формировать ошибочные прецеденты решения ![]() . Для контроля эффективности коррекции базы знаний на основе набора ошибочных прецедентов решения формируется множество контрольных прецедентов
. Для контроля эффективности коррекции базы знаний на основе набора ошибочных прецедентов решения формируется множество контрольных прецедентов ![]() , где
, где ![]() – решение, удовлетворяющее критериям качества. Необходимо скорректировать результаты нечеткого вывода таким образом, чтобы при исходных данных
– решение, удовлетворяющее критериям качества. Необходимо скорректировать результаты нечеткого вывода таким образом, чтобы при исходных данных ![]() отклонение от контрольного решения
отклонение от контрольного решения ![]() было минимально, т. е.
было минимально, т. е. ![]() .
.
В качестве основы алгоритма нечеткого вывода целесообразно выбрать алгоритм Суджено, поскольку в этом случае поверхность отклика при нечетком выводе строится в виде линейной комбинации гиперплоскостей, образующихся на этапе логического вывода в соответствии с выражением
 , (1)
, (1)
что дает возможность дополнительного построения детализирующих гиперплоскостей, таких что
![]() . (2)
. (2)
Анализ работ [2], [3] показывает возможность представления функции многих переменных в виде линейной комбинации функций одного переменного. Тогда можно полагать, что при вычислении значения целевой функции каждая определяющая переменная осуществляет вклад в итоговое значение функции независимо от других переменных, т.е. результат нечеткого вывода может быть представлен в виде
 , (3)
, (3)
где l – порядок (уровень) приближения, ![]() – вклад переменной
– вклад переменной ![]() в значение F на l-ом уровне приближения. С точки зрения формулы (3) этап логического вывода Суджено обеспечивает приближение к функции
в значение F на l-ом уровне приближения. С точки зрения формулы (3) этап логического вывода Суджено обеспечивает приближение к функции ![]() на первом и единственном уровне приближения при
на первом и единственном уровне приближения при ![]() в окрестности действия продукционного правила. Для обеспечения сходимости (3) и получения приближения на уровнях
в окрестности действия продукционного правила. Для обеспечения сходимости (3) и получения приближения на уровнях ![]() используем аналогию аппроксимации функции одной переменной с помощью базисных функций системы Фабера-Шаудера. Для проведения обобщения функций Фабера-Шаудера для случая функции многих переменных необходимо обеспечить разбиение
используем аналогию аппроксимации функции одной переменной с помощью базисных функций системы Фабера-Шаудера. Для проведения обобщения функций Фабера-Шаудера для случая функции многих переменных необходимо обеспечить разбиение ![]() на зоны
на зоны![]() , где l – уровень разбиения, d – индекс зоны на уровне l в соответствии с требованиями:
, где l – уровень разбиения, d – индекс зоны на уровне l в соответствии с требованиями:
| (4) |
Вид обобщенной функции Фабера-Шаудера показан на рис. 2.
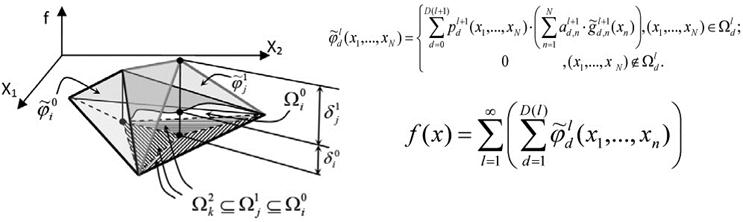
Рис. 2. Вид обобщенной функции Фабера-Шаудера
С учетом аппроксимации поверхности отклика нечеткого вывода с помощью обобщенной функции Фабера-Шаудера выражение (2) может быть представлено в виде
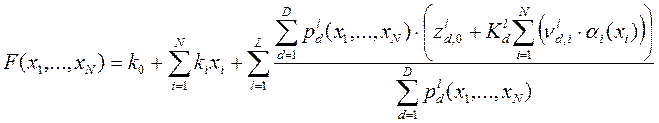 , (5)
, (5)
где ![]() - коэффициенты, выбираемые в зависимости от положения контрольных прецедентов
- коэффициенты, выбираемые в зависимости от положения контрольных прецедентов ![]() .
.
Покажем преимущества модифицированного алгоритма Суджено на примере фрагмента ЭС анализа выполнения маневра самолета «верхний двойной вираж» (см. рис. 3).

Рис. 3. Общий вид маневра «верхний двойной вираж»
Задача атакующего самолета при выполнении маневра «верхний двойной вираж» - осуществить сближение с целью, осуществляющей оборонительный вираж в горизонтальной плоскости, с выходом на допустимые условия атаки. Эффективность маневра оценивается в процентах по 4 показателям. Большее значение показателя соответствует лучшему варианту выполнения маневра. Также для эффективного маневра необходимо, чтобы значения показателей E2 и E3 принимали значение более 85 %. На рис. 4 (сверху) показаны графики функций управляющих воздействий для угла крена, полученные при использовании традиционного алгоритма Суджено, его проведенной модификации и соответствующие выбранному «эталонному» маневру. Можно заметить, что в окрестностях 3 и 15 секунды располагается область решений, в которой применение традиционного алгоритма Суджено приводит к получению значительной погрешности 10..20 градусов по углу крена, что сказывается на снижении показателей качества (см. рис. 4, снизу).
Учет контрольных прецедентов с помощью обобщенных функций Фабера-Шаудера позволил, не модифицируя первоначально созданные экспертом определения в базе знаний ЭС, осуществить коррекцию результатов нечеткого вывода и добиться увеличения значения показателей E2 и E3 до уровня выше 85 %.
Таким образом, использование модифицированного алгоритма нечеткого вывода Суджено, основанного на внесении поправки на этапе логического вывода с помощью обобщенных функций Фабера-Шаудера, позволяет осуществить коррекцию нечеткого решения в соответствии с требованиями контрольных прецедентов, не изменяя первоначально заданные экспертные определения в базе знаний ЭС.
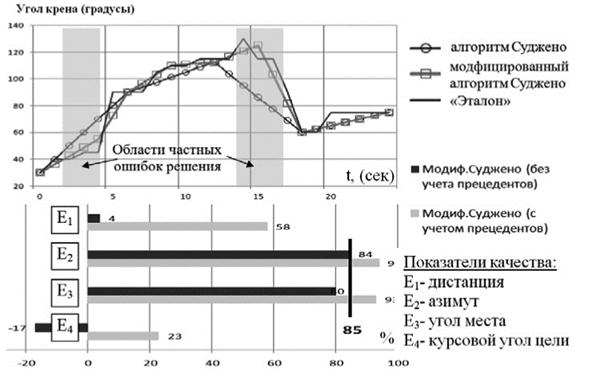
Рис. 4. Значения угла крена и показатели качества маневра с учетом модели редукции ошибки
Литература
1. Тельнов Ю.Ф. Интеллектуальные информационные системы/ Московский международный институт эконометрики, информатики, финансов и права.–М.,2004.–82с.
2. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения // Докл. АН СССР .– 1957.– Т. 114 .– с.953-956
3. Кашин Б.С., Саакян А.А. Ортогональные ряды.–М.:АФЦ,1999.– 560с.
Публикации с ключевыми словами: экспертная система, база знаний, алгоритм нечеткого вывода Суджено, обобщенные функции Фабера-Шаудера
Публикации со словами: экспертная система, база знаний, алгоритм нечеткого вывода Суджено, обобщенные функции Фабера-Шаудера
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




