научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК 519.81
МГТУ им. Н.Э. Баумана
iu5.root@gmail.com
Введение.
Системы оперативной обработки запросов клиентов, построенные не базе ЛВС (СООЗК), находят широкое применение во всех областях народного хозяйства. Условно эти системы можно разбить на следующие группы:
- системы обслуживания звонков клиентов (так называемые CallCenter). К их числу следует отнести справочные службы, обслуживающие телефонные звонки клиентов.
- системы обслуживания запросов клиентов (так называемые СОЗаК). К их числу следует отнести центры обслуживания продаж электроэнергии, центры мобильной связи, телефонные узлы и т.д. Эти организации имеют несколько рабочих мест (окон), за которыми находятся специалисты, которые отвечают на запросы клиентов.
- системы обслуживания заказов клиентов (так называемые СОЗК). К их числу следует отнести салоны сервисного обслуживания компьютерной техники, салоны оперативной полиграфии и т.д.
Количество граждан, имеющих ноутбуки и пользующихся услугами салонов компьютерной техники, постоянно растет. Также постоянно растет количество граждан и организаций, которые для печати полиграфической продукции, например, визиток, бланков, этикеток, ярлыков, приглашений, ценников, листовок пользуются услугами полиграфических предприятий. При этом следует иметь в виду, что постоянно растут потребности граждан в улучшении качества их обслуживания, как клиентов. Это требует уменьшения как времени пребывания клиентов в офисе, так и времени выполнения их заказов, а также дальнейшего непрерывного совершенствования сервиса услуг, которые предоставляют клиентам.
В связи с этим необходимо иметь простую для использования аналитическую модель, позволяющую, для систем оперативной обработки запросов клиентов, оценивать эффективность их функционирования и давать рекомендации по построению, модернизации или реорганизации этих систем.
Формализация работы систем оперативной обработки запросов клиентов.
Формально описать работу СОЗаК и СООЗК можно в виде системы массового обслуживания (СМО). При этом клиентов следует представить в виде заявок, поступающих на обслуживание в СМО, а сотрудников этих организаций в видеаппаратов, обслуживающих эти заявки.
Тогда организационную структуру работы этих систем удобно представить в виде многоканальной СМО с количеством обслуживающих аппаратов “C” (равным количеству сотрудников, обслуживающих клиентов), с бесконечной очередью и дисциплиной обслуживания в порядке поступления. Согласно [1-5] входной поток заявок в СМО следует считать пуассоновским, а время обслуживания этих заявок распределенным экспоненциально. Условно СМО такого типа обозначают сокращенно как М/М/С, при этом все аппараты считаются одинаковыми.
Анализ существующей модели анализа многоканальной СМО.
В настоящее время для анализа многоканальной СМО типа М/М/С в основном применяют стандартную аналитическую модель, которая позволяет определить загрузку обслуживающего аппарата системы, среднее количество заявок в очереди и системе (в очереди и на обслуживании), среднее время нахождения заявок как в очереди, так и в СМО. Эта модель предполагает использование ряда математических выражений в следующей последовательности [1-5]:
1) Определяем вероятность (![]() ) того, что в СМО отсутствуют заявки.
) того, что в СМО отсутствуют заявки.
 (1)
(1)
![]() - количество аппаратов, обслуживающих поступающие на вход СМО заявки;
- количество аппаратов, обслуживающих поступающие на вход СМО заявки;
![]() - загрузка одного аппарата СМО
- загрузка одного аппарата СМО ![]()
![]() - загрузка всех аппаратов СМО
- загрузка всех аппаратов СМО ![]() где
где ![]()
2) Определяем вероятность (![]() ) того, что обслуживают заявки только (i) аппаратов СМО, где
) того, что обслуживают заявки только (i) аппаратов СМО, где ![]()
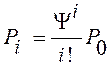 (2)
(2)
3) Определяем вероятность (![]() ) того, что заняты обслуживанием заявок все аппараты и кроме этого (i) заявок находится в очереди, где
) того, что заняты обслуживанием заявок все аппараты и кроме этого (i) заявок находится в очереди, где ![]()
 (3)
(3)
4) Определяем среднее количество заявок в очереди
 (4)
(4)
5) Определяем среднее количество заявок в системе (в очереди и на обслуживании)
![]() (5)
(5)
6) Определяем среднее время ожидания заявок в очереди (![]() )
)
 (6)
(6)
7) Определяем среднее время пребывания заявок в СМО (![]() )
)
![]() (7)
(7)
Анализ приведенных выражений показывает, что модель не совсем удобна для практического использования, особенно в инженерной практике.
Постановка задачи.
Необходимо разработать более простую и более удобную в использовании, чем набор выражений (1) – (7), аналитическую модель для анализа СМО типа М/М/С .
Разработка аналитической модели.
При разработке аналитической модели для вычисления основных характеристик функционирования многоканальной СМО типа М/М/С предлагается использовать метод сведения загрузки многоканальной СМО к загрузке одноканальной СМО, учитывающий помощь обслуживающих аппаратов друг другу при наличии в очереди заявок, которые следует обслужить.
В этом случае, например, для СМО типа М/М/2, в которой только два аппарата, справедливы следующие зависимости:
![]() - загрузка одного аппарата многоканальной СМО, т.е. вероятность загрузки любого аппарата;
- загрузка одного аппарата многоканальной СМО, т.е. вероятность загрузки любого аппарата;
![]() - вероятность, что аппарат свободен и может помочь другому аппарату в обслуживании заявок при наличии заявок в очереди к СМО. В случае двух аппаратов также имеем, что
- вероятность, что аппарат свободен и может помочь другому аппарату в обслуживании заявок при наличии заявок в очереди к СМО. В случае двух аппаратов также имеем, что ![]() - вероятность, что свободный аппарат может помочь занятому в обслуживании заявок, находящихся в очереди;
- вероятность, что свободный аппарат может помочь занятому в обслуживании заявок, находящихся в очереди;
Тогда загрузка аппарата одноканальной СМО, заменяющей эквивалентную ей двухканальную СМО, будет уменьшена на величину этой помощи, и равна ![]()
Далее будем использовать этот принцип замены для трех и более аппаратов. При этом для упрощения вычислений не будем учитывать. одновременную помощь нескольких аппаратов выделенному одному аппарату Для трех аппаратов в этом случае получаем ![]() и так далее В результате получаем, что загрузка аппарата в одноканальной СМО, заменяющей эквивалентную ей “С” канальную СМО будет приближенно равна
и так далее В результате получаем, что загрузка аппарата в одноканальной СМО, заменяющей эквивалентную ей “С” канальную СМО будет приближенно равна ![]()
В этом случае аналитические выражения для определения основных характеристик “С” канальной СМО будут иметь следующий вид
 (8)
(8)
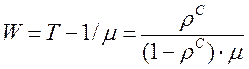 (9)
(9)
Далее используя формулу Литтла и учитывая ,что ![]() , имеем
, имеем
 (10)
(10)
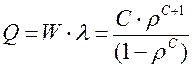 (11)
(11)
![]() - среднее время пребывания заявки в “С” канальной СМО
- среднее время пребывания заявки в “С” канальной СМО
![]() - среднее время нахождения заявки в очереди в “С” канальной СМО
- среднее время нахождения заявки в очереди в “С” канальной СМО
![]() - среднее количество заявок, находящихся в очереди и на обслуживании в “С” канальной СМО
- среднее количество заявок, находящихся в очереди и на обслуживании в “С” канальной СМО
![]() - среднее количество заявок, находящихся в очереди в “С” канальной СМО
- среднее количество заявок, находящихся в очереди в “С” канальной СМО
При этом следует иметь в виду, что ![]()
Оценка погрешности аналитической модели.
Сравнительный анализ полученных в работе выражений (8)-(11) и существующих (точных выражений) (1)-(7) показал, что при С=2 полученные выражения также дают точный результат , и лишь при С > 2 результаты являются приближенными. При этом приближенные значения основных характеристик функционирования “С” канальной СМО несколько меньше точных значений, Это указывает на то, что реальная эквивалентная загрузка аппарата будет несколько больше чем величина.![]() .
.
Для значений ![]() при С < 6 это различие составляет менее 5% и с ростом загрузки аппарата многоканальной СМО эта погрешность существенно уменьшается.
при С < 6 это различие составляет менее 5% и с ростом загрузки аппарата многоканальной СМО эта погрешность существенно уменьшается.
Точные выражения для проведения быстрого анализа СМО типа М/М/С.
Для быстрого и точного анализа широко используемых на практике многоканальных СМО типа М/М/С, с количество аппаратов менее шести, из выражений (4)- (7) получены простые выражения, которые имеют следующий вид
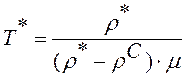 (12)
(12)
 (13)
(13)
Далее используя формулу Литтла и учитывая , что ![]() имеем
имеем
 (14)
(14)
 (15)
(15)
Выражения для вычисления ![]() в зависимости от числа аппаратов многоканальной СМО типа М/М/С приведены ниже в таблице
в зависимости от числа аппаратов многоканальной СМО типа М/М/С приведены ниже в таблице
Таблица 1.
Выражения для вычисления загрузки СМО.
Значения С | Значения |
С=1 | |
С=2 | |
С=3 | |
С=4 | |
С=5 | |
Выводы.
1. Предложена аналитическая модель для анализа организационных структур систем оперативной обработки запросов клиентов, формализуемых в виде СМО типа М/М/С.
2. Разработанная аналитическая модель содержит простые и удобные для практического использования приближенные выражения для оценки основных характеристик функционирования СМО типа М/М/С.. Погрешность вычисления среднего числа заявок и среднего времени их пребывания в СМО составляет менее 5%. С ростом загрузки СМО эта погрешность уменьшается.
3. Для быстрого и точного анализа широко используемых на практике многоканальных СМО типа М/М/С, с количеством обслуживающих аппаратов не более пяти, получены и приведены точные и достаточно простые аналитические выражения.
Литература
1. Денисов А.А., Колесников Д.Н. Теория больших систем управления. – Л.: Энергоиздат. 1982.- 288 с.
2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман Н.М. Исследование операций в экономике. – М.: Маркет ДС 2007 – 408 с.
3. Лабскер Л.Г. , Бабешко Л.О. Теория массового обслуживания в экономической сфере. – М.: ЮНИТИ. 1998 – 319 с.
4. Лебедев А.И., Чернявский Е.А. Вероятностные методы в вычислительной технике. – М.: Высшая школа. 1986.- 312 с.
5. Фомин Г.П. Математические методы и модели в коммерческой деятельности –М.: Финансы и статистика. 2009. -642 с.
Публикации с ключевыми словами: массовое обслуживание, запросы клиентов, многоканальные системы
Публикации со словами: массовое обслуживание, запросы клиентов, многоканальные системы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



