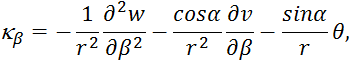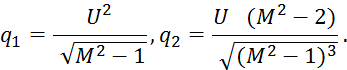научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК 004.4
Мордовский государственный университет им. Н. П. Огарева
Разрушение авиационных и ракетных конструкций может происходить не только из-за развития в них чрезмерных напряжений или из-за потери статической устойчивости, но и вследствие динамической неустойчивости в сверхзвуковом потоке газа, т.е. флаттера. Явления флаттера, связанные с элементами обшивки летательных аппаратов, принято относить к категории панельного флаттера (или флаттера пластин и оболочек) [1].
Задача о флаттере включает в себя несколько аспектов (рис. 1):
· аэродинамический, связанный с определением параметров потока на поверхности обтекаемого тела;
· упругий, связанный с анализом напряженно-деформированного состояния конструкции под действием внешних нагрузок;
· инерционный, связанный с необходимостью учета сил инерции.
Рис. 1. Основные аспекты решения задачи о флаттере
В теории панельного флаттера известны два вида флаттера: связанный и одномодовый. Первый возникает при слиянии частот колебаний оболочки в комплексной плоскости при больших числах Маха. Сравнение границ флаттера связанного типа с экспериментами при M>1.7 удовлетворительное [2]. Одномодовый флаттер возникает при 1<M<2 и изучен в настоящее время слабо, поскольку требует для своего исследования привлечения уточненной аэродинамической теории, а это сопряжено со значительными математическими трудностями [1].
Цель данной работы состоит:
· в разработке методики, алгоритма и программной реализации для решения задачи о связанном флаттере для осесимметричной оболочки с меридианом в виде Безье-сплайна, при этом толщина оболочки вдоль меридиана также предполагается заданной Безье-функцией;
· в создании программной среды для дальнейшего исследования оболочек рассматриваемого класса в отношении флаттера одномодового типа.
Программное обеспечение, разрабатываемое нами в этих целях, назовем условно FlutterWorks. В такой постановке для решения задачи лучше всего подходит метод конечных элементов (МКЭ), а задача в целом дополняется еще двумя аспектами:
· геометрическим, предполагающим создание геометрической модели оболочки, удобной для ее последующей дискретизации;
· алгебраическим, связанным с решением несимметричной квадратичной обобщенной задачи на собственные значения высокого порядка и с матрицей блочно-ленточной структуры.
Одной из особенностей современного этапа развития САПР в целом и, в частности, CAE-систем [3], является открытость их архитектуры, что дает возможность, используя средства API, разрабатывать специализированные библиотеки, расширяющие и дополняющие базовый функционал САПР.
В качестве такой системы мы выбрали SolidWorks (SolidWorksFlowWorksSimulation). В этом смысле данная работа является продолжением работы [4]. Тогда рассматриваемая задача реализуется в виде следующей последовательности этапов:
1. Формирование геометрической модели оболочки, т.е. геометрический аспект, включающий в себя процедуру считывания параметров геометрии модели SolidWorks из дерева конструирования, в частности, координат ключевых точек сплайнов (рис. 2 а). Эта функция реализуется специальным программным модулем, разработанным на базе APISolidWorks.
2. Решение аэродинамической задачи средствами FlowWorksSimulation с последующим импортом результатов решения в FlutterWorks (аэродинамический аспект). Эту функцию также реализует специальный программный модуль, разработанный на базе API FlowWorksSimulation (рис. 2 б).
3. Формирование конечноэлементной модели для решения задачи о флаттере осесимметричной оболочки рассматриваемого типа.
4. Решение обобщенной квадратичной несимметричной задачи на собственные значения.
| |
(а) | (б) |
Рис. 2. Геометрия оболочки и аэродинамический аспект задачи | |
Геометрический аспект задачи и конечноэлементная дискретизация.
После того как координаты ![]() и
и ![]() ключевых точек сплайнов модели считаны из дерева конструирования, (
ключевых точек сплайнов модели считаны из дерева конструирования, (![]() ,
, ![]() – количество ключевых точек, задающих образующую оболочки), конечноэлементная дискретизация не представляет собой никаких трудностей. В качестве конечного элемента рассматривается усеченный конус, и координаты конечноэлементных узлов согласно [5] определяются следующим образом:
– количество ключевых точек, задающих образующую оболочки), конечноэлементная дискретизация не представляет собой никаких трудностей. В качестве конечного элемента рассматривается усеченный конус, и координаты конечноэлементных узлов согласно [5] определяются следующим образом:
 ,
,
 ,
,
где
![]() , здесь
, здесь
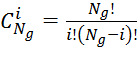 , ,
, , ![]() .
.
Густота сетки задается при этом величиной шага для параметра ![]() . Толщина оболочки определяется аналогично одномерной Безье-Функцией в следующем виде:
. Толщина оболочки определяется аналогично одномерной Безье-Функцией в следующем виде:
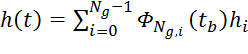 , ,
, ,
где
![]() , здесь
, здесь
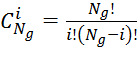 ,
,  ,
, ![]()
![]() – координаты ключевых точек на числовой оси,
– координаты ключевых точек на числовой оси, ![]() ,
, ![]() – количество ключевых точек, задающих распределение толщины вдоль образующей. Таким образом, геометрическая модель оболочки в целом задается ключевыми точками Безье в двух подпространствах: в двумерном для образующей и одномерном для толщины.
– количество ключевых точек, задающих распределение толщины вдоль образующей. Таким образом, геометрическая модель оболочки в целом задается ключевыми точками Безье в двух подпространствах: в двумерном для образующей и одномерном для толщины.
К сожалению, базовый функционал SolidWorks не предусматривает возможности формирования оболочки, толщина которой была бы задана Безье-функцией, поэтому координаты ключевых точек для толщины задаются в виде уравнений, а визуализация оболочки в целом осуществляется в отдельном окне. Все связанные с названными обстоятельствами особенности построения конечноэлементной сетки иллюстрирует собой рис. 3.
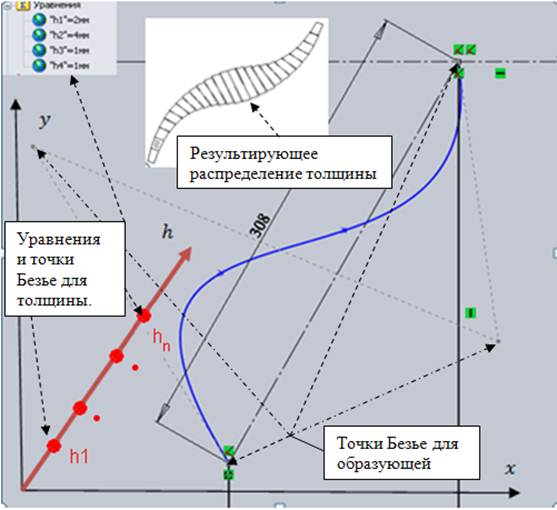
Рис. 3. Конечноэлементная дискретизация
Конечноэлементная модель.
Как уже указывалось, для решения рассматриваемой задачи в качестве конечного элемента используется усеченный конус. На рис. 4 показаны компоненты перемещений и внутренних силовых факторов, имеющих место в поперечных и меридиональных сечениях оболочки. Конечный элемент построен на основе теории С.П.Тимошенко с учетом деформации поперечного сдвига в меридиональном направлении [6]. Таким образом, для неосесимметричной деформации имеем:
|
(1) |
Здесь ![]() ,
, ![]()
![]()
![]() −компоненты линейной деформации в срединной поверхности соответственно в меридиональном, окружном направлении и деформация сдвига;
−компоненты линейной деформации в срединной поверхности соответственно в меридиональном, окружном направлении и деформация сдвига; ![]() ,
, ![]() ,
, ![]() −параметры изменения кривизн и кручения,
−параметры изменения кривизн и кручения, ![]() –деформация поперечного сдвига в меридиональном направлении; u, w, v,– компоненты перемещений соответственно в тангенциальном, радиальном направлении и в направлении, касательном к параллельному кругу,
–деформация поперечного сдвига в меридиональном направлении; u, w, v,– компоненты перемещений соответственно в тангенциальном, радиальном направлении и в направлении, касательном к параллельному кругу, ![]() −угол поворота сечения, нормального к срединной поверхности;
−угол поворота сечения, нормального к срединной поверхности; ![]() −координата вдоль образующей,
−координата вдоль образующей, ![]() −угловая координата в плоскости параллельного круга,
−угловая координата в плоскости параллельного круга, ![]() −угол полураствора конуса,
−угол полураствора конуса, ![]() −радиус параллельного круга. На рис. 4 показаны также внутренние силовые факторы: перерезывающая сила Q, продольные силы Nsи Nb , изгибающие моменты Ms и Mβсоответственно в меридиональном и окружном направлении.
−радиус параллельного круга. На рис. 4 показаны также внутренние силовые факторы: перерезывающая сила Q, продольные силы Nsи Nb , изгибающие моменты Ms и Mβсоответственно в меридиональном и окружном направлении.
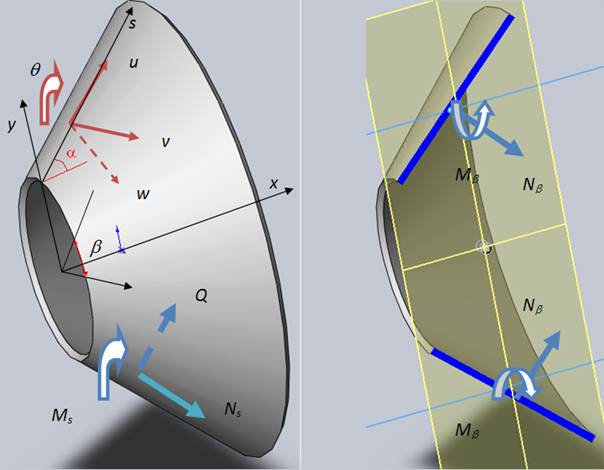
Рисунок 4. Конечный элемент оболочки
Тогда уравнение колебаний конечного элемента оболочки можно получить на основе принципа Гамильтона и в соответствии со стандартной процедурой МКЭ имеем [7]:
![]() ,
,
где
![]() ,
,
![]() .
.
Здесь ![]() − матрица жесткости конечного элемента, N– матрица формы [7], построенная в данном случае в предположении о кубическом характере изменения перемещений w внутри элемента, D – матрица упругости; m – матрица масс конечного элемента, ρ−плотность материала оболочки,
− матрица жесткости конечного элемента, N– матрица формы [7], построенная в данном случае в предположении о кубическом характере изменения перемещений w внутри элемента, D – матрица упругости; m – матрица масс конечного элемента, ρ−плотность материала оболочки, ![]() – круговая частота колебаний; B – матрица дифференциальных операторов, построенная на основе разложения компонент перемещений в ряд Фурье по окружной координате, а также на основе уравнений (1). Таким образом,
– круговая частота колебаний; B – матрица дифференциальных операторов, построенная на основе разложения компонент перемещений в ряд Фурье по окружной координате, а также на основе уравнений (1). Таким образом, ![]() и
и ![]() –вектор амплитуд для перемещений, t–время, а
–вектор амплитуд для перемещений, t–время, а ![]() Интегрирование ведется для первого интеграла по срединной поверхности элемента S, для второго – по объему элемента V.
Интегрирование ведется для первого интеграла по срединной поверхности элемента S, для второго – по объему элемента V.
Объединяя вклад каждого конечного элемента на основе принципа прямой жесткости, и осуществляя преобразование перемещений к общей системе координат, получим для ансамбля элементов следующее уравнение:
| (2) |
где ![]() - матрица жесткости,
- матрица жесткости, ![]() - матрица масс,
- матрица масс, ![]() - вектор амплитуд перемещений для узловых точек. Все указанные в данном случае матрицы и вектор относятся к ансамблю конечных элементов. Уравнение (2) представляет собой обобщенную симметричную задачу на собственные значения. Для ее решения используется известная процедура, основанная на следствии из теоремы об инерции Сильвестра [7], согласно которой количество отрицательных элементов на главной диагонали матрицы уравнения (2) после приведения ее к треугольному виду методом Гаусса при заданном значении
- вектор амплитуд перемещений для узловых точек. Все указанные в данном случае матрицы и вектор относятся к ансамблю конечных элементов. Уравнение (2) представляет собой обобщенную симметричную задачу на собственные значения. Для ее решения используется известная процедура, основанная на следствии из теоремы об инерции Сильвестра [7], согласно которой количество отрицательных элементов на главной диагонали матрицы уравнения (2) после приведения ее к треугольному виду методом Гаусса при заданном значении ![]() , указывает число собственных значений, расположенных левее заданного в спектре. Дальнейшее определение нужного собственного значения в спектре определяется сочетанием методов хорд и «золотого сечения».
, указывает число собственных значений, расположенных левее заданного в спектре. Дальнейшее определение нужного собственного значения в спектре определяется сочетанием методов хорд и «золотого сечения».
Тестовая задача 1. С целью тестирования разработанного программного обеспечения была решена задача по определению собственных частот колебаний жестко защемленной на торцах усеченной конической оболочки со следующими параметрами: меньший торцевой радиус ![]() =0.67 м., больший торцевой радиус RL=334.5 м., длина по оси
=0.67 м., больший торцевой радиус RL=334.5 м., длина по оси ![]() =0.15266 м., толщина (неизменная по меридиану)
=0.15266 м., толщина (неизменная по меридиану) ![]() =0.001 м., модуль Юнга
=0.001 м., модуль Юнга ![]() =1.98e+11 Па, коэффициент Пуассона
=1.98e+11 Па, коэффициент Пуассона ![]() =0.31, плотность материала
=0.31, плотность материала ![]() =7850.0 кг/м3.
=7850.0 кг/м3.
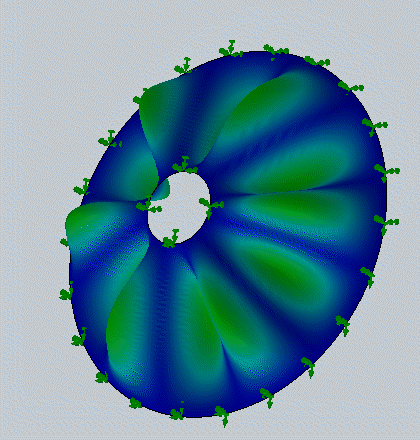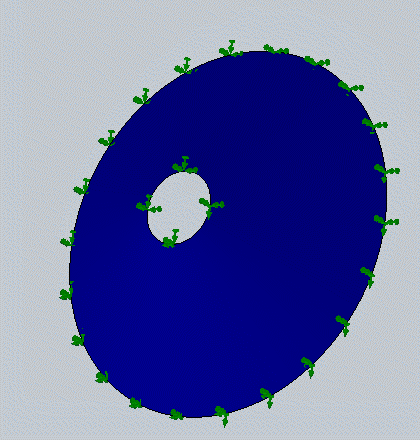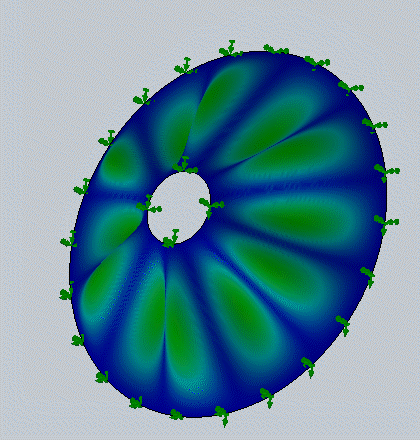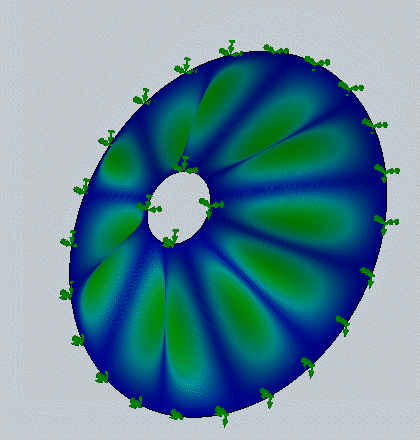
На рис. 5 и 6 показано сравнение результатов решения этой задачи для различных гармоник и форм колебаний по меридиану с известным экспериментальным и аналитическим решением этой задачи [8] и результатами SolidWorksSimulation. Следует отметить совпадение этих решений с относительной погрешностью не более 2 %.

Рис. 5. Результаты решения задачи анализа колебаний конической оболочки
|
|
Рис. 6 Результаты решения задачи анализа колебаний конической оболочки в сравнении с результатами SolidWorksSimulation | |
Флаттер оболочки. Будем использовать для определения аэродинамической нагрузки поршневую теорию:
| (3) |
Здесь ![]() – динамическое давление потока,
– динамическое давление потока, ![]() –плотность газа, U–скорость потока, M– число Маха. В этом случае на основе принципа Гамильтона уравнение флаттера для ансамбля конечных элементов приобретает следующий вид [9]:
–плотность газа, U–скорость потока, M– число Маха. В этом случае на основе принципа Гамильтона уравнение флаттера для ансамбля конечных элементов приобретает следующий вид [9]:
| (4) |
В этом уравнении Aи D- матрицы ансамбля конечных элементов, соответственно аэродинамической жесткости, и аэродинамического демпфирования. A и ![]() формируются аналогично K и M на основе принципа прямой жесткости, при этом для конечных элементов имеем
формируются аналогично K и M на основе принципа прямой жесткости, при этом для конечных элементов имеем ![]() − матрица аэродинамической жесткости конечного элемента ,
− матрица аэродинамической жесткости конечного элемента , ![]() − матрица аэродинамического демпфирования конечного элемента. Матрица Aнесимметрична и собственные значения рассматриваемой задачи
− матрица аэродинамического демпфирования конечного элемента. Матрица Aнесимметрична и собственные значения рассматриваемой задачи ![]() комплексны. Здесь также использованы обозначения:
комплексны. Здесь также использованы обозначения:
| (5) |
При этом следует иметь в виду, что параметры (![]() ,
, ![]() и
и ![]() ) соответствуют возмущенному около оболочки потоку.
) соответствуют возмущенному около оболочки потоку.
Порядок уравнения (4) высок, но матрицы имеют блочно-ленточную структуру. Тогда, следуя В.Г.Бунькову [10], есть смысл перейти к обобщенным координатам, в качестве которых использовать собственные векторы задачи (2), т.е. формы колебаний оболочки в вакууме. Учитывая ортогональность собственных форм и, нормируя их по кинетической энергии ![]() , где
, где ![]() −матрица, составленная из rсобственных векторов, а
−матрица, составленная из rсобственных векторов, а ![]() − единичная матрица, получаем уравнение флаттера в обобщенных координатах:
− единичная матрица, получаем уравнение флаттера в обобщенных координатах:
| (6) |
где ![]() ,
, ![]() - диагональная матрица, содержащая собственные значения, т.е. квадраты частот, соответствующих колебаниям в вакууме
- диагональная матрица, содержащая собственные значения, т.е. квадраты частот, соответствующих колебаниям в вакууме ![]()
![]()
![]() …
… ![]() на главной диагонали,
на главной диагонали, ![]() ,
, ![]() ,
,![]() - собственный вектор, соответствующий обобщенным координатам.
- собственный вектор, соответствующий обобщенным координатам.
Дальнейшее решение сводится к анализу изменения собственных значений задачи (6) при возрастании параметра (плотности) потока. При этом используется дифференциальный прогноз, т.е. для каждого следующего собственного значения ![]() , соответствующего плотности
, соответствующего плотности ![]() , решение получается исходя из предыдущего
, решение получается исходя из предыдущего ![]() , соответствующего плотности
, соответствующего плотности ![]() (
(![]() , и двигаясь в направлении производной
, и двигаясь в направлении производной
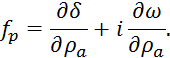
Для определения производной сформируем сопряженную систему:
| (7) |
где ![]() - собственный вектор сопряженной задачи. Уравнения (6) и (7) эквивалентны следующим уравнениям:
- собственный вектор сопряженной задачи. Уравнения (6) и (7) эквивалентны следующим уравнениям:
![]() .
.
в этих формулах
 ,
,  ,
,  .
.
Тогда производная от собственного значения по плотности потока определяется в виде:
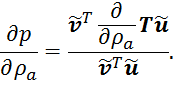
Cоответственно, очередное собственное значение аппроксимируется как

здесь ![]() , а затем это собственное значение и соответствующие собственные векторы прямой и сопряженной задачи уточняются при помощи следующих итерационных процессов:
, а затем это собственное значение и соответствующие собственные векторы прямой и сопряженной задачи уточняются при помощи следующих итерационных процессов:
 ,
,
 ,
,

Здесь
![]()
![]() – наибольший по модулю компонент вектора
– наибольший по модулю компонент вектора ![]()
![]() – номер компонента,
– номер компонента, ![]() −отношение
−отношение ![]() -ных компонент векторов
-ных компонент векторов ![]() и
и ![]() ,
, ![]() – единичная матрица.
– единичная матрица.
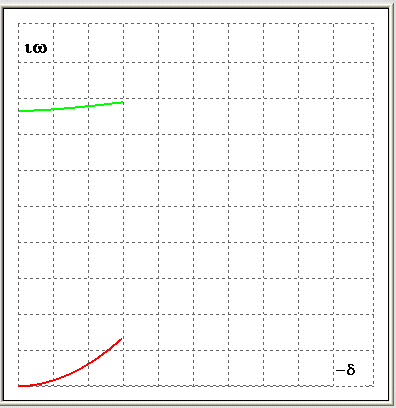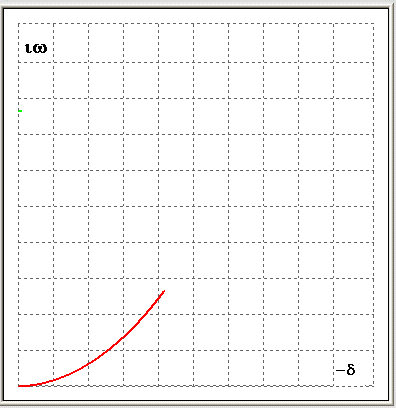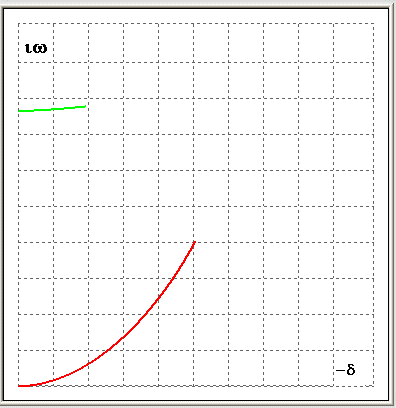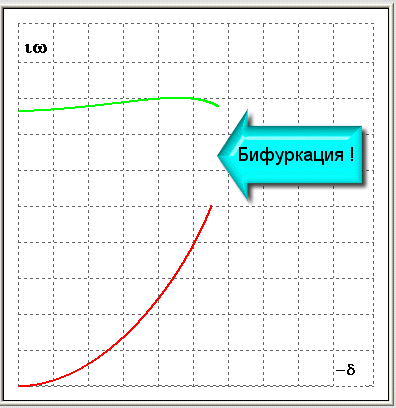
При возрастании плотности потока собственные значения сближаются друг с другом и при некотором критическом значении становятся кратными (близкими к кратным), такая ситуация называется бифуркационной. Затем одно из собственных значений выходит на положительную полуплоскость, чему соответствуют колебания с возрастающей амплитудой, т.е. флаттер. На рис. 7 показаны годографы нескольких низших комплексных частот (рис. 7а), а также бифуркационная ситуация для частот, движущихся навстречу друг другу в более крупном масштабе (рис. 7 б).
Тестовая задача 2. С целью тестирования разработанного программного обеспечения была решена задача по определению границы флаттера жестко защемленной на торцах усеченной конической оболочки со следующими параметрами: меньший торцевой радиус ![]() =0.04 м., больший торцевой радиус
=0.04 м., больший торцевой радиус ![]() =0.0556 м., длина по оси
=0.0556 м., длина по оси ![]() =0.06258 м., толщина (неизменная по меридиану)
=0.06258 м., толщина (неизменная по меридиану) ![]() =0.00003 м., модуль Юнга
=0.00003 м., модуль Юнга ![]() =1.28e+11 Па, коэффициент Пуассона
=1.28e+11 Па, коэффициент Пуассона ![]() =0.25, плотность материала
=0.25, плотность материала ![]() =8000.0 кг/м3. При этом в наших расчетах q1и q2 определялись следующим образом:
=8000.0 кг/м3. При этом в наших расчетах q1и q2 определялись следующим образом: ![]() ,
, ![]() , где
, где ![]() и
и ![]() определяются так же, как и
определяются так же, как и ![]()
![]() в (5), но в качестве
в (5), но в качестве ![]() в этих формулах, а также в качестве Mи Uв (5) берутся местные значения параметров для конечного элемента, соответствующие возмущенному потоку (рис. 8);
в этих формулах, а также в качестве Mи Uв (5) берутся местные значения параметров для конечного элемента, соответствующие возмущенному потоку (рис. 8); ![]() и
и ![]() соответствуют парметрам потока на бесконечности, при которых реализуется данное возмущенное состояние,
соответствуют парметрам потока на бесконечности, при которых реализуется данное возмущенное состояние, ![]() в (4), а также
в (4), а также ![]() и
и ![]() определяются как текущие значения соответственно плотности потока и коэффициентов на бесконечности (число Маха на бесконечности
определяются как текущие значения соответственно плотности потока и коэффициентов на бесконечности (число Маха на бесконечности ![]() и
и ![]() ). В работах [11, 12] для определения аэродинамического давления для фиксированного значения угла полураствора конуса (
). В работах [11, 12] для определения аэродинамического давления для фиксированного значения угла полураствора конуса (![]() =14°) производилась замена в (3) коэффициента
=14°) производилась замена в (3) коэффициента ![]() на
на ![]() , где
, где ![]() ,
, ![]() - динамическое давление на бесконечности. Результаты, представленные на рис. 9, были получены нами для ряда разных высот стандартной атмосферы, т.е. для разных значений
- динамическое давление на бесконечности. Результаты, представленные на рис. 9, были получены нами для ряда разных высот стандартной атмосферы, т.е. для разных значений ![]() и, соответственно,
и, соответственно,![]() при постепенном возрастании
при постепенном возрастании ![]() . Максимальная относительная разность их по отношению друг к другу и к результатами [11, 12] не превышала 1,2 %, что свидетельствует об адекватности результатов решения аэродинамической задачи средствами SolidWorksFlowWorksSimulation действительным значениям параметров обтекания. Частотные годографы (рис. 7) соответствуют этой же задаче.
. Максимальная относительная разность их по отношению друг к другу и к результатами [11, 12] не превышала 1,2 %, что свидетельствует об адекватности результатов решения аэродинамической задачи средствами SolidWorksFlowWorksSimulation действительным значениям параметров обтекания. Частотные годографы (рис. 7) соответствуют этой же задаче.
|
|
(а) | (б) |
Рис. 7. Частотные годографы | |
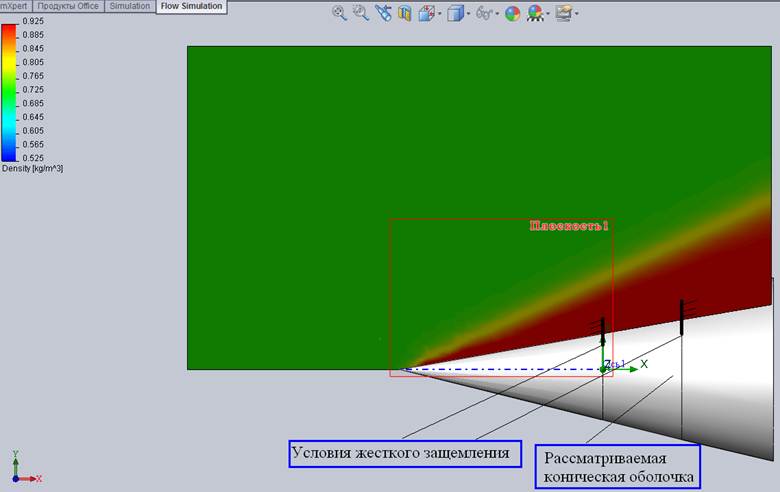
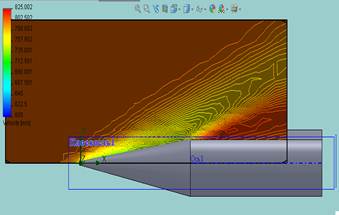
Рис. 8. Возмущенный около оболочки поток. Распределение плотности потока.

Рис. 9. Критическое значение динамического давления, соответствующее наступлению флаттера
Пример. Задача 3. Рассмотрим задачу определения границы флаттера для почти конической оболочки с такими же параметрами, как и в Задаче 2, но являющейся элементом составной конструкции (рис. 10) и заданной сплайном. От конической оболочки Задачи 2 эта оболочка отличается тем, что в точках сопряжения сплайна, являющимся ее меридианом, заданы условия касательности с дугой окружности на левом торце и с прямой – на правом торце.
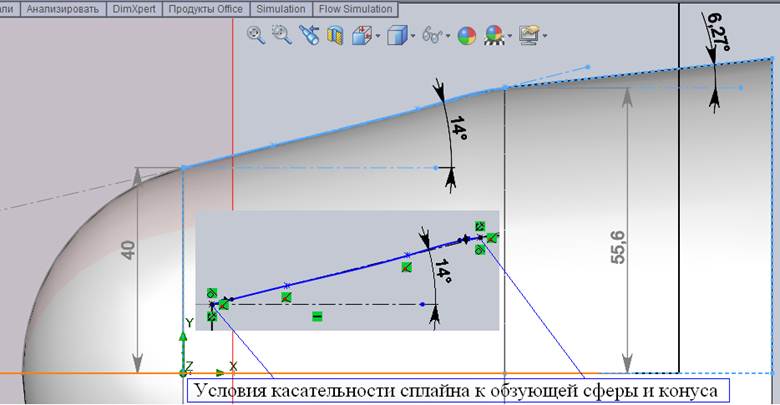
Рис. 10. Составная оболочечная конструкция
На рис. 11 показан характер распределения плотности потока при обтекании конструкции (получено средствами FlowWorksSimulation), а граница флаттера, как показывают наши расчеты, изменилась по сравнению с Задачей 2 существенным образом: динамическое давление флаттера на бесконечности, соответствующее сочетанию первой и второй формы колебаний, составило ![]() и реализуется со значением номера гармоники
и реализуется со значением номера гармоники ![]() . Наинизшее динамическое давление составило
. Наинизшее динамическое давление составило ![]() и соответствует сочетанию четвертого и пятого тонов при
и соответствует сочетанию четвертого и пятого тонов при ![]() .
.
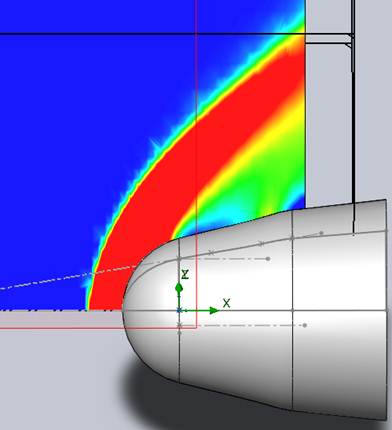
Рис. 11. Качественный характер распределения плотности потока около обтекаемой оболочки (получено средствами FlowWorksSimulation)
Программная реализация. Структура программного обеспечения в целом приведена на рис. 12. AddInмодуль создает COM-интерфейс и через соответствующую структуру данных передает основной указатель
m_iSldWorks = CComQIPtr<ISldWorks, &__uuidof(ISldWorks)>(ThisSW); на API SolidWorks Application. Этот же модуль обеспечивает создание в меню SolidWorksпункта MechanicsOptimum– Flutter, при обращении к которому производится загрузка основного dll-модуля FLUTTER.DLL. Функции API приложения FlowWorksSimulationреализованы в динамической библиотеке NIKCommonApi.dll, а доступ к ним организуется посредством созданного в нашей программной среде пространства имен:
#import "NIKCommonApi.dll"
namespace API = NIKCommonApiLib;
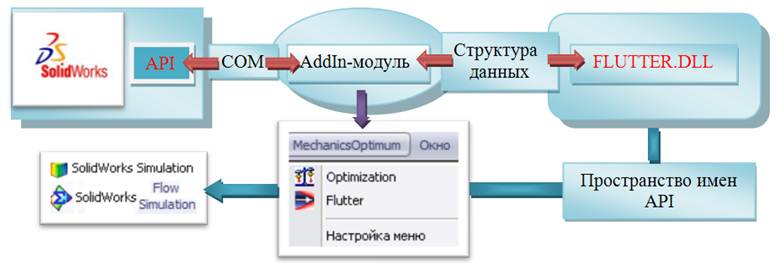
Рис. 12. Структура программного обеспечения
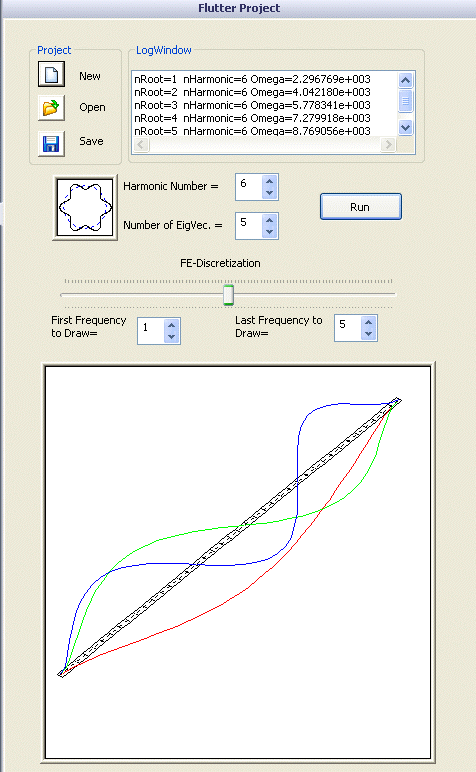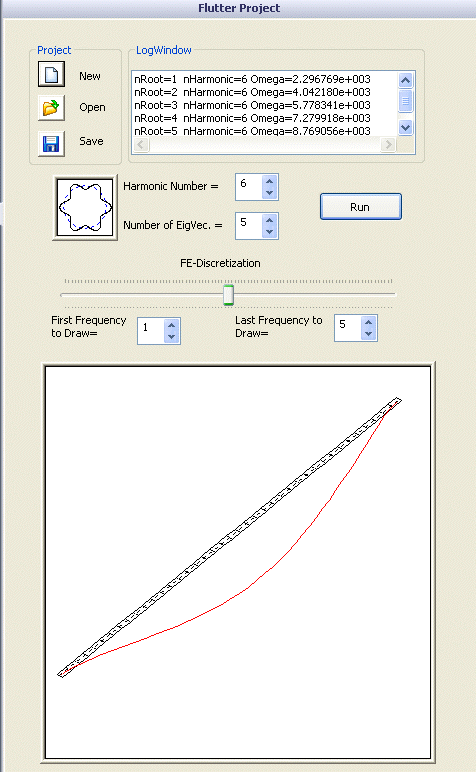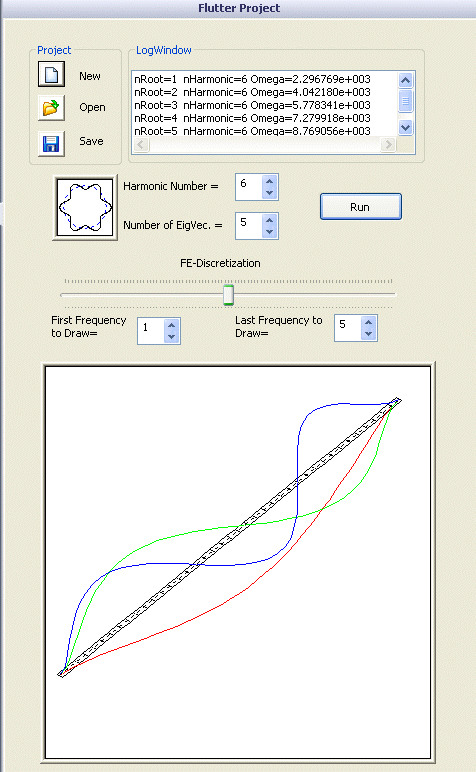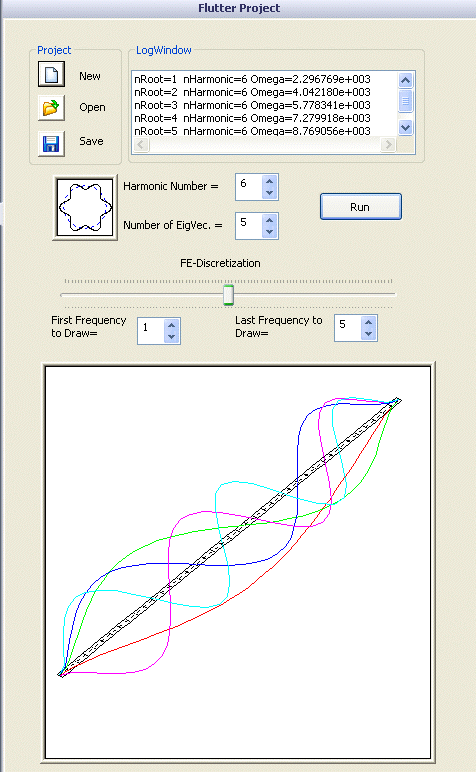
Интерфейс пользователя (рис. 6) полностью встроен в окно TaskPaneSolidWorks.
Работа выполнена в соответствии с базовым соглашением о сотрудничестве с компанией SolidWorksRussiaи партнерской программой SolidWorksCorp. Partner (Research).
Автор выражает признательность сотрудникам компании SolidWorksRussiaД.Б. Собянину и И.В. Щекину за квалифицированную техническую поддержку, оказанную в процессе выполнения данной работы.
Литература:
1. Алгазин С.Д., Кийко И.А. Флаттер пластин и оболочек. Ин-т проблем механики РАН. – М.: Наука, 2006. 247 с.
2. Веденеев В.В. Численное исследование сверхзвукового флаттера пластины с использованием точной аэродинамической теории //Механика жидкости и газа. 2009, № 2. С.169-178.
3. Норенков И. П. Основы автоматизированного проектирования: учеб. для вузов. — 4-е изд., перераб. и доп.— М.: Изд-во МГТУ им. Н. Э. Баумана, 2009. 430 с.
4. Чугунов М. В., Небайкина Ю. А. Программный модуль для решения задач оптимального проектирования в среде SolidWorks на базе API //Наука и образование: электронное научно-техническое издание, 2011, № 9. (<http://technomag.edu.ru/doc/206217.html>).
5. Шикин Е.В., Плис А.И. Кривые и поверхности на экране компьютера. – М.: «Диалог», МИФИ, 1996. 280 с.
6. Королев В.И. Слоистые анизотропные пластины и оболочки из армированных пластмасс. – М.:Машиностроение, 1965. 272 с.
7. Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов: Пер. с англ. М.: Стройиздат, 1982. 447с.
8. Кольман Э.Р. Экспериментальное исследование собственных частот колебаний стальных усеченных конических оболочек вращения // В кн.: Расчеты на прочностью – М.: Машиностроение, 1968. – Вып. 8.
9. Вольмир А.С. Оболочки в потоке жидкости и газа. Задачи гидроупругости. – М.: Наука, 1979. 387 с.
10. Буньков В.Г. Проблема собственных значений матриц в задаче о флаттере // Труды ЦАГИ. 1978.Т. 17, № 2. С. 93-99.
11. Sunder P.J., Ramakrishnan C.V., Sengupta S. Optimum cone angles in aeroelastic flutter // Comp. and Struct. 1983. Vol.17, N 1. P. 25-29.
12. Ueda T., Kobayashi S., Kihira M. Supersonic Flutter of Truncated Conical Shells. // Trans. Jap. Soc. Aer. Sp. Sci. 1977. V.20, N 47. P.13 -30.
Публикации с ключевыми словами: метод конечных элементов, САПР, SolidWorks, API, флаттер осесимметричной оболочки, Безье-сплайны, аэродинамическое давление, поршневая теория, обобщенная несимметричная задача на собственные значения, COM-интерфейс
Публикации со словами: метод конечных элементов, САПР, SolidWorks, API, флаттер осесимметричной оболочки, Безье-сплайны, аэродинамическое давление, поршневая теория, обобщенная несимметричная задача на собственные значения, COM-интерфейс
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||