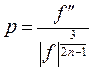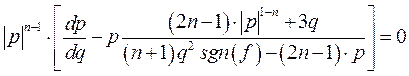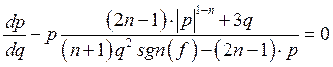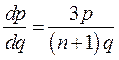научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
УДК 519.624
МГТУ им. Н.Э. Баумана
Применение в технике жидкостей сложного состава приводит к необходимости рассматривать жидкости со сложными механическими свойствами. Такие жидкости могут проявлять свойства упругости, пластичности, памяти, зависимости кажущейся вязкости от интенсивности скорости их деформирования и много других свойств, отличающих их от обычной ньютоновской жидкости. Для описания механических свойств чисто вязких жидкостей (то есть без предельного напряжения сдвига, наличие которого определяет свойство пластичности) широко применяется степенная модель Оствальда – де Виля, которая в случае простого сдвигового течения записывается в виде
 ,
,
где ![]() - касательное напряжение,
- касательное напряжение, ![]() - поперечная координата,
- поперечная координата, ![]() - скорость (в случае простого сдвига
- скорость (в случае простого сдвига ![]() ),
), ![]() - постоянная консистенции,
- постоянная консистенции, ![]() - индекс течения,
- индекс течения, ![]() соответствует ньютоновской жидкости.
соответствует ньютоновской жидкости.
Если ![]() , то жидкость называется псевдопластической, так как ее «кажущаяся вязкость»
, то жидкость называется псевдопластической, так как ее «кажущаяся вязкость»  убывает с увеличением скорости деформации.
убывает с увеличением скорости деформации.
Если ![]() , то кажущаяся вязкость возрастает с увеличением скорости деформации. Это свойство экспериментально зафиксировано у некоторых полимерных растворов и называется «дилатансией». Соответствующие жидкости называются дилатантными.
, то кажущаяся вязкость возрастает с увеличением скорости деформации. Это свойство экспериментально зафиксировано у некоторых полимерных растворов и называется «дилатансией». Соответствующие жидкости называются дилатантными.
Известны многочисленные примеры применения реологического закона Оствальда – де Виля к теории пограничного слоя. В частности, при описании пограничного слоя на полубесконечной пластине (задача Блазиуса), слоя смешения спутных потоков несмешивающихся жидкостей и других. Во всех рассматриваемых случаях задача является автомодельной.
Если в качестве зависимой переменной выбрать функцию ![]() , пропорциональную функции тока:
, пропорциональную функции тока:  , и независимую переменную
, и независимую переменную  , то в конечном итоге, указанный класс задач теории пограничного слоя сводится к исследованию обыкновенного нелинейного дифференциального уравнения
, то в конечном итоге, указанный класс задач теории пограничного слоя сводится к исследованию обыкновенного нелинейного дифференциального уравнения
| (1) |
(Здесь 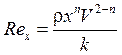 - обобщенное число Рейнольдса,
- обобщенное число Рейнольдса, ![]() - продольная координата,
- продольная координата, ![]() - плотность жидкости,
- плотность жидкости, ![]() - характерная скорость, в случае задачи Блазиуса она равна скорости набегающего потока.) То есть, уравнение (1) описывает целый класс автомодельных течений теории нелинейного пограничного слоя.
- характерная скорость, в случае задачи Блазиуса она равна скорости набегающего потока.) То есть, уравнение (1) описывает целый класс автомодельных течений теории нелинейного пограничного слоя.
Для качественного исследования уравнения (1) сведем его к уравнению первого порядка. Перепишем это уравнение в инвариантных переменных (вид этих «инвариантных» переменных был получен методами группового исследования в [1])
| (2) |
Уравнение (1) в переменных (2) переписывается в виде
| (3) |
Следует отметить, что уравнение (3) при n>1 всегда имеет в качестве решения алгебраический корень ![]() . Этому корню соответствует однородное течение жидкости с
. Этому корню соответствует однородное течение жидкости с ![]() . Анализ второго сомножителя, то есть уравнения
. Анализ второго сомножителя, то есть уравнения
| (4) |
позволяет установить, что здесь также возможно особое решение p= 0, но лишь при 1<n<2.
Таким образом, исследование выбранного класса решений уравнения нелинейного пограничного слоя сводится к исследованию поведения интегральных кривых уравнения (4). Для качественного представления решений уравнения (4) удобно использовать двулистную фазовую плоскость с координатами (p, q), один из листов которой соответствует положительным значениям функции f, а другой – отрицательным. При этом достаточно исследовать поведение интегральных кривых на одном листе фазовой плоскости, тогда на другом их ход можно указать в силу симметрии. Мы ограничимся случаем sgn(f) > 0.
Поведение интегральных кривых для конечных значений p, qподробно исследовано в [1], [2]. Из результатов качественного анализа следует, что проблема существования множества решений или их отсутствия может быть связана именно с переходом с одного листа фазовой плоскости на другой, когда значения функции f проходят через ноль. Поэтому представляет интерес получение асимптотических представлений для сепаратрис семейств интегральных кривых при ![]() .
.
Анализ показывает существование двух сепаратрис при q→ -∞, p→0. Соответствующее асимптотическое представление следует искать в виде зависимости
![]() ,
, 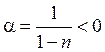 ,
,  ,
,
что подтверждается непосредственной проверкой.
Для доказательства существования двух других сепаратрис при p®¥ удобно перейти к новым переменным ![]() ,
,  ,
,  В новых переменных уравнение (4) записывается в виде
В новых переменных уравнение (4) записывается в виде
| (5) |
Нетрудно показать, что уравнение (5) имеет две интегральные кривые, являющиеся сепаратрисами семейств интегральных кривых и входящих в точку на прямой z=0 при ![]() , соответствующее асимптотическое представление которых в переменных (p, q) имеет вид
, соответствующее асимптотическое представление которых в переменных (p, q) имеет вид  .
.
Для исследования поведения интегральных кривых вблизи бесконечно удаленной точки, в областях, не примыкающих к оси p=0 и не лежащих между найденными выше сепаратрисами, будем предполагать, что выполнены сильные неравенства
 и
и ![]() .
.
Тогда уравнение (4) асимптотически эквивалентно уравнению
| (6) |
Уравнение (6) позволяет определить асимптотический вид указанных интегральных кривых
![]() ,
, 
с произвольной постоянной a, ![]() . Для дальнейшего следует отметить, что показатель
. Для дальнейшего следует отметить, что показатель ![]() при
при ![]() и
и ![]() при
при ![]() .
.
Для подтверждения полученных качественных результатов относительно вида интегральных кривых желательно указать «простой» пример, решение которого можно получить аналитически. Такая возможность имеется при ![]() , так как уравнение (1) сводится линейному уравнению (в пределах листа)
, так как уравнение (1) сводится линейному уравнению (в пределах листа)
| (7) |
А именно, рассмотрим конкретную задачу о смешении двух спутных потоков одинаковой жидкости, один из которых вначале был неподвижным. Для решения уравнения (7) это означает выполнение условия ![]() при
при ![]() , а также граничных условий
, а также граничных условий
| (8) |
Как показывает анализ сформулированной краевой задачи, основанный на аналитическом решении уравнения (7), выполнение граничных условий (8) возможно только при ![]() и
и ![]() , где
, где ![]() и
и ![]() . После проведения расчетов был получен окончательный вид решения уравнения (7), удовлетворяющий указанным условиям:
. После проведения расчетов был получен окончательный вид решения уравнения (7), удовлетворяющий указанным условиям:
 ,
,
где ![]() ,
,![]() ,
, ![]() для отрезка
для отрезка ![]() , причём
, причём ![]() ,
, ![]() .
.
Вне этого отрезка решение должно быть продолжено следующим образом: при ![]()
![]() и
и ![]() при
при ![]() соответственно.
соответственно.
На рис. 1 изображен вид интегральных кривых, рассчитанных численно по уравнению (4), в проекции на круг (проекция нижней полусферы Пуанкаре на плоскость переменных (p,q)) для n=2. Там же указана выделенная кривая, соответствующая приведенному точному решению частной задачи, находящаяся в полном соответствии с качественным анализом.
В рамках построенной модели, для уравнения (1) при ![]() были найдены решения следующей краевой задачи
были найдены решения следующей краевой задачи
![]()
![]() ,
, ![]() , и
, и ![]() ,
, ![]() , ξ→ξ+ (ξ+>0).
, ξ→ξ+ (ξ+>0).

Рис. 1. Качественный вид интегральных кривых в проекции на круг (проекция нижней полусферы Пуанкаре на плоскость переменных (p,q)) для рассмотренного случая n=2.
Эта краевая задача соответствует задаче Блазиуса с отрицательной скоростью, пропорциональной постоянной ![]() на поверхности обтекаемой пластины. Известно [3], что решение такой задачи может быть неединственным или не существовать вовсе. В рамках модели дилатантной жидкости анализ возникающей проблемы проводится до конца аналитически.
на поверхности обтекаемой пластины. Известно [3], что решение такой задачи может быть неединственным или не существовать вовсе. В рамках модели дилатантной жидкости анализ возникающей проблемы проводится до конца аналитически.
На самом деле, результаты проведенного исследования свидетельствуют о том, что решения уравнения (1) с такими граничными условиями существуют при ![]() только если
только если ![]() . Число решений для одних и тех же граничных условий равно 2.
. Число решений для одних и тех же граничных условий равно 2.
При этом можно выделить два случая.
1) Для значений ![]() оба решения задачи имеют одинаковый вид
оба решения задачи имеют одинаковый вид
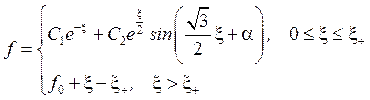
где 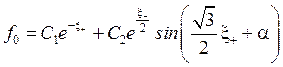 .
.
Например, при ![]() :
:
первое решение имеет вид
 ,
,
второе решение имеет вид
 .
.
Графики решений в первом случае, их первых и вторых производных вблизи точки ![]() представлены рис. 2
представлены рис. 2

Рис. 2. Графики решений, их первых и вторых производных при ![]()
2) Для значений ![]() решения имеют разный вид.
решения имеют разный вид.
Первое решение имеет прежний качественный вид


Рис. 3. Графики решений, их первых и вторых производных при ![]() .
.
Второе решение является «составным»

Например, при ![]() первое решение
первое решение

второе решение

Графики решений во втором случае, их первых и вторых производных вблизи точки ![]() представлены на рис. 3
представлены на рис. 3
Таким образом, приведенные примеры показывают, что на основе применения модели дилатантной жидкости можно эффективно демонстрировать качественные методы анализа нелинейных процессов переноса, так как имеется одновременная возможность построения аналитических решений.
Литература.
1. Жижин Г.В., Уфимцев А.А. О течениях в плоском ламинарном пограничном слое дилатантных жидкостей // Изв. АН СССР. МЖГ. 1977. №5. С. 164-167.
2. Павлов К.Б., Шахорин А.П. К вопросу о пространственной локализации ламинарного пограничного слоя в неньютоновской дилатантной жидкости // Изв. АН . МЖГ. 2007. №1. С. 51-57.
3. Черный Г.Г. Пограничный слой на пластине с подвижной поверхностью // Докл: АН СССР, 1973. Т. 213. №4. С. 802-803.
Публикации с ключевыми словами: пограничный слой, точное аналитическое решение, неньютоновская жидкость
Публикации со словами: пограничный слой, точное аналитическое решение, неньютоновская жидкость
Смотри также:
- Расчетно–экспериментальное исследование сверхзвукового турбулентного отрывного течения и локальной теплоотдачи в плоском канале с внезапным расширением
- Анализ физической адекватности численного расчета коэффициента восстановления температуры при различных вариантах постановки задачи
- Расчет тепловых потоков на поверхности затупленных тел
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||