научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
УДК.62-522.2
МГТУ им. Н.Э. Баумана
Введение
В настоящее время вопросам разработки математических моделей и методик расчета конструктивных параметров пневмогидравлических устройств (ПГУ) подвески автомобилей посвящено большое количество работ [1, 2, 3 и др.].
Наряду с расчетными методами исследования внутренней динамики ПГУ с использованием имитационного математического моделирования окончательное заключение о работоспособности конструкции и правильности выбора настроек могут дать только натурные испытания. Натурные испытания также позволяют верифицировать имитационные математические модели – оценить их адекватность и точность.
Натурные испытания пневмогидравлических рессор (ПГР) могут проводиться в составе изделия (пробеговые испытания машины), и на стенде. Стендовые испытания дают возможность получить наиболее общую картину процессов, протекающих в исследуемой ПГР, так как позволяют нагружать рессору любым необходимым воздействием, замерять все необходимые параметры и оперативно менять настройки и регулировки - объемы камер, заправочные давления, дроссельную систему.
Целью работы является разработка и экспериментальная проверка адекватности математической модели двухообъемной ПГР, а также исследование нагрузочных и тепловых характеристик рессоры в стендовых условиях нагружения.
Первый раздел статьи посвящен разработке математической модели двухообъемной ПГР. Во втором разделе приведено описание стендовой установки для испытания рессоры. Третий раздел включает в себя результаты испытания исследуемой ПГР и анализ полученных экспериментальных данных. В приложении размещены динамические нагрузочные характеристики ПГР, полученные как экспериментально, так и расчетные характеристики для тех же условий нагружения.
1. Математическая модель двухобъемной пневмогидравлической рессоры
В работе проведены исследования характеристик двухобъемной ПГР (рис. 1) как методами имитационного моделирования, так и в процессе стендовых испытаний. Технические характеристики исследуемой рессоры приведены в таблице 1.
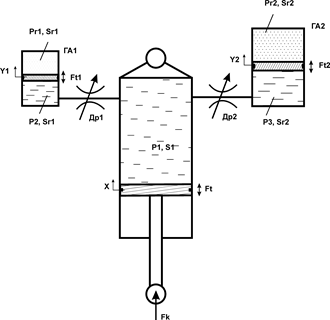
Рис. 1. Расчетная схема двухобъемной гидропневматической рессоры
Таблица 1
Характеристики пневмогидравлической рессоры
Параметр | Размер-ность | Значения |
Диаметр поршня гидроцилиндра Dп | м | 0,14 |
Диаметр штока гидроцилиндра Dшт | м | 0,115 |
Полный ход поршня гидроцилиндра hmax | м | 0,9 |
Объем малой пневмокамеры V02 | л | 0,87 |
Объем большой пневмокамеры V01 | л | 2,7 |
Заправочное давление малой пневмокамеры p02 | МПа | 3,3 |
Заправочное давление большой пневмокамеры p01 | МПа | 3,3 |
Площадь дросселирующего отверстия малой пневмокамеры fдр2 | м2 | 3,8×10-5 |
Площадь дросселирующего отверстия большой пневмокамеры fдр1 | м2 | 9,5×10-5 |
1.1. Общие положения
При построении математической модели используем следующие допущения: отсутствуют утечки рабочей жидкости (РЖ); волновые процессы в трубопроводах отсутствуют; температура РЖ постоянна (т.е. постоянными считаем коэффициенты кинематической вязкости и силы трения); потери на трение в магистралях и обратном клапане, золотнике и другой аппаратуре не учитываются; давление в сливной магистрали равно нулю; радиальный зазор между втулкой и золотником в золотниковых распределителях принимаем равным нулю; рабочие кромки считаем острыми; принимаем, что соединительные каналы велики по сечению и коротки по длине; постоянным принимаем модуль упругости РЖ.
Уравнение неразрывности выражает закон сохранения массы движущейся жидкости. Для двух поперечных сечений одного и того же потока идеальной жидкости (рис. 2) уравнение неразрывности можно записать в виде
Q1 = Q2, (1)
где Q1, Q2– расходы жидкости через сечения 1 и 2.

Рис. 2. Схема сечений потока рабочей жидкости
Уравнение (1) показывает, что в любом сечении потока при установившемся движении несжимаемой РЖ расход ее постоянен.
Расход жидкости через дроссель связан с перепадом давления на входе и выходе известной зависимостью [4, 5]
 (2)
(2)
где µ - коэффициент расхода; fдр – площадь проходного сечения дросселя; (р1-р2) - перепад давлений; ρ – плотность рабочей жидкости.
Коэффициент расхода µ золотникового дросселя зависит от числа Рейнольдса и условий подхода потока к рабочему окну. Для идеального золотникового дросселя можно принять µ = 0,73 … 0,75 [6].
Уравнение движения подвижных элементов составляют на основании основного закона динамики - второго закона Ньютона
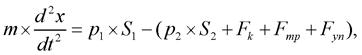 (3)
(3)
где m - приведенная к поршню масса подвижных частей и РЖ; p1, p2, - давление в полостях гидроцилиндра; S1, S2 - эффективные площади поршня в поршневой и штоковой полостях гидроцилиндра; Fk – внешняя нагрузка; Fmp - сила трения; Fуп – сила, действующая со стороны цилиндра на поршень при достижении им упоров; x - перемещение поршня.
При вычислении силы трения Fmp следует отметить, что ее величина, в общем случае, зависит от большого числа факторов, таких как вид трения, рабочее давление, температура, шероховатость поверхностей, геометрические и физико-механические характеристики уплотнений и др. [7, 8]. Ввиду значительных давлений в зоне контакта уплотнений поршней и штоков пневмогидравлических устройств, обусловленных большим предварительным натягом, их трение можно считать сухим или гранично-сухим [8].
В математических моделях элементов ПГУ зависимость силы сухого трения от скорости относительного перемещения контактирующих поверхностей задается в виде, показанном на рис. 3.
Сила Fmp приближенно описывается равенством [9]
![]() (4)
(4)
где Fc – кулоновское трение; kb – коэффициент изменения силы страгивания;
cv – коэффициент перевода.
Кулоновское трение определяется зависимостью
![]() (5)
(5)
где Fpr – сила трения покоя; fcfr – коэффициент силы кулоновского трения;
pA, pB – давление в полостях гидроцилиндра ПГР.
Для того чтобы избежать разрыва функции Fmp(v) при dx/dt=0, вводится небольшая область abs[dx/dt] ≤ vthв окрестности нулевого значения скорости, где сила трения прямо пропорциональна скорости:
![]() (6)
(6)
 (7)
(7)
Здесь vth - скорость на границе введенной области.
Численные значения параметров в формулах (4) – (7), принятые при моделировании, приведены в таблице 2.
Таблица 2
Численные значения параметров, принятых при моделировании
Параметр | Обозначение | Размерность | Значение |
Сила трения покоя | Fpr | Н | 1 500 |
Коэффициент силы | fcfr | Н/бар | 33 |
Коэффициент изменения | kb | -- | 1,1 |
Коэффициент перевода | cv | с/м | 10 |
Начальное давление газа в поршневой полости ПГР | pA | кПа | 13,5×103 |
Начальное давление газа в штоковой полости ПГР | pB | кПа | 45×102 |
Вид зависимости силы, действующей на поршень со стороны упоров в цилиндре, представлен на рис. 4.
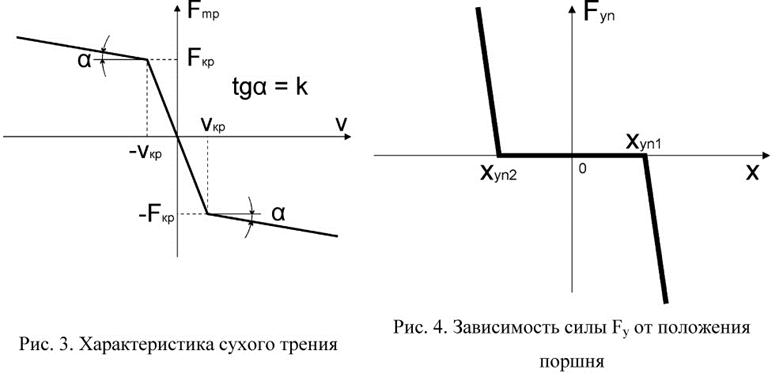
Таким образом, формула для расчета Fуп имеет вид
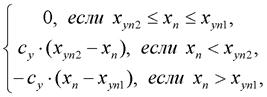 (8)
(8)
где xуп1, xуп2 – координаты упоров в цилиндре; cу – жесткость упора.
Для полости цилиндра связь между давлением и балансом расходов определяется формулой [9]
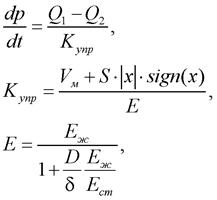 (9)
(9)
где р – давление в полости цилиндра; Q1 и Q2– расходы рабочей жидкости на входе и выходе рассматриваемой полости; Купр – коэффициент упругости полости с жидкостью; Vм – «мертвый» объем полости цилиндра, т.е. объем рабочей жидкости, оставшейся в цилиндре при максимальном ходе поршня; S – площадь цилиндра; x – перемещение поршня; Е – приведенный объемный модуль упругости рабочей жидкости в упругой оболочке цилиндра; Еж – объемный модуль упругости рабочей жидкости; D, δ – диаметр и толщина стенки цилиндра; Ест – модуль упругости материала стенки цилиндра.
Для вычисления силы, действующей на поршень со стороны газа, необходимо знать уравнение состояния газа. Упругая характеристика газовой полости определяется как зависимость между действующей силой Fупр и смещением поршня х. В соответствии с первым законом термодинамики [9]
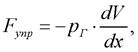 (10)
(10)
где рГ – текущее значение избыточного давления газа в газовой полости; V – текущее значение объема газовой полости.
При работе «газовой пружины» возможны различные условия теплообмена между газом, находящимся в полости пневмогидравлического устройства, и окружающей средой. При хорошем теплообмене процессы, протекающие в объеме камеры, могут быть близкими к изотермным [9]. Однако в общем случае изменение состояния газа в зависимости от продолжительности процесса и конкретных условий окружающей среды может происходить по разным законам. При этом во всех случаях должно удовлетворяться уравнение состояния идеального газа. Такими процессами являются политропические процессы, характеризуемые уравнением
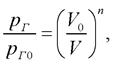 (11)
(11)
где рГ и рГ0 – текущее и начальное значение давления газа в полости соответственно; V и V0 – текущее и начальное значение объема газовой полости; n – показатель политропы.
С достаточной для практики точностью можно принять в расчетах показатель политропы n = 1,25…1,28 [9].
1.2. Математическая модель двухобъемной ПГР
Расчетная схема рессоры приведена на рис. 1. Запишем выражения для расходов в полостях ПГР:
![]() (12)
(12)
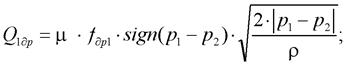 (13)
(13)
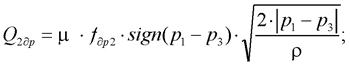 (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
Здесь Q1 – расход рабочей жидкости в полости гидроцилиндра за счет перемещения поршня; Q1др, Q2др - расходы рабочей жидкости через дроссели 1 и 2 соответственно; Q1Г, Q2Г - расходы рабочей жидкости в полостях гидроаккумуляторов 1 и 2 соответственно; S1Г, S2Г – площади цилиндров гидроаккумуляторов 1 и 2 соответственно.
Уравнения для давлений в полостях ПГР имеют вид
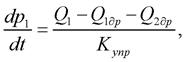 (17)
(17)
 (18)
(18)
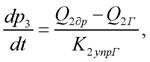 (19)
(19)
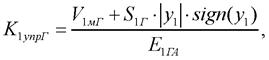 (20)
(20)
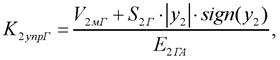 (21)
(21)
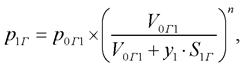 (22)
(22)
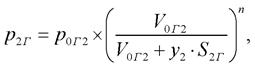 (23)
(23)
где К1упрГ, К2упрГ – коэффициенты упругости полостей с жидкостью гидроаккумуляторов 1 и 2 соответственно; V1мГ, V2мГ – «мертвые» объемы полостей гидроаккумуляторов 1 и 2 соответственно; Е1ГА, Е1ГА – приведенные объемные модули упругости рабочей жидкости в упругой оболочке цилиндров гидроаккумуляторов 1 и 2 соответственно; р1Г, р2Г – текущие значения давлений газа в полостях гидроаккумуляторов 1 и 2 соответственно; р0Г1, р0Г1 - начальные значения давлений газа в полостях гидроаккумуляторов 1 и 2 соответственно.
Движение поршня совместно с колесом МКМ описывается выражением
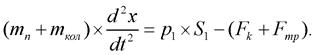 (24)
(24)
Здесь mn - масса поршня цилиндра ПГР; mкол – масса колеса МКМ.
Движение поршней-разделителей может быть описано уравнениями
 (25)
(25)
 (26)
(26)
где m1n-p, m1n-p – массы поршней-разделителей гидроаккумуляторов 1 и 2 соответственно; F1mp, F2mp - сила трения в гидроаккумуляторах 1 и 2 соответственно.
Совместное решение уравнений (12) – (26) полностью описывает рабочие процессы, протекающие в пневмогидравлической рессоре с противодавлением.
2. Описание установки для испытаний
Испытания ПГР проводились в ГНЦ РФ ФГУП «НАМИ». Для испытаний использовался электрогидравлическом стенде POZ 0317 фирмы Schenk. Параметры стенда приведены в таблице 3.
Таблица 3
Параметры стенда
Параметр | Величина |
Ход гидроцилиндра, мм | 250 |
Максимальная пиковая скорость штока гидроцилиндра, м/с | 0,5 |
Максимальная динамическая сила гидроцилиндра, кН | ±100 |
Частотный диапазон, Гц | 0 - 30 |
Высота от пазовых плит до штока гидроцилиндра в среднем положении, мм | 1200 |
Мертвая зона хода штока по краям диапазона, мм | 15 |
Чувствительность датчика перемещений штока, мм/в | 12,5 |
Чувствительность датчика силы, кН/в | 10 |
Для испытаний рабочий цилиндр ПГР был закреплен на штатных сферических шарнирах на гидроцилиндре, головка без соединительного шланга была соединена со штоком, головка со шлангом соединялась с датчиком силы, установленным на неподвижном основании под гидроцилиндром. Такой способ установки исключал из измерений силы инерции движущихся частей рабочего гидроцилиндра и позволял измерять только упругие и демпфирующие компоненты силы, развиваемой гидроцилиндром. Пневмокамеры были расположены на расстоянии 800 мм от рабочего цилиндра и были соединены с ним рукавом высокого давления.
Сила рабочего цилиндра и перемещение его корпуса регистрировались с помощью системы сбора данных B+ SMultidata и далее обрабатывались.
На рис. 5 представлен внешний вид стенда с закрепленной на нем ПГР, на рис. 6…8 – компоненты стенда и испытуемой ПГР.
3. Описание эксперимента
3.1. Исследование упругой (статической) характеристики ПГР
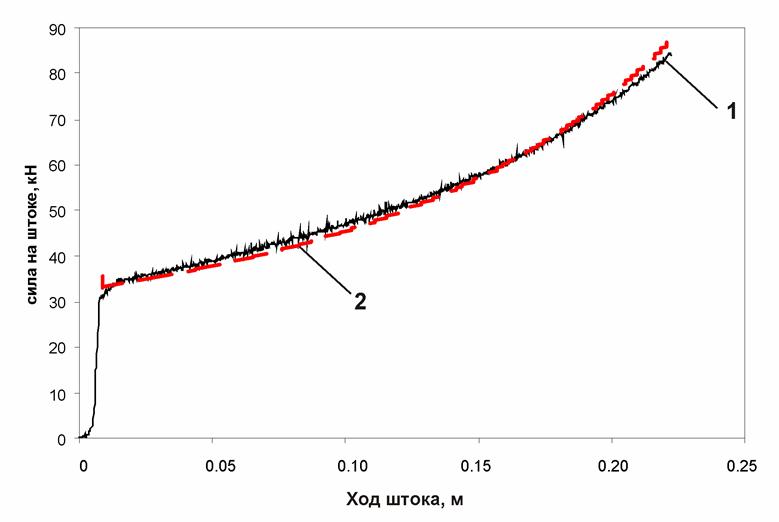
Во время стендовых испытаний шток ПГР перемещался от среднего положения (ход штока 0,12 м) до полностью вдвинутого, а затем – до полностью выдвинутого со скоростью не более 1мм/с. При этом измерялись сила на штоке и ход штока.
После обработки полученных записей был построен график зависимости силы на штоке ПГР от перемещения штока (рис. 9).
|
| |
Рис. 5. Стенд для испытания ПГР | Рис. 6. Датчик силы | |
|
| |
Рис. 7. Блок пневмоцилиндров испытуемой ПГР | Рис. 8. Аппаратура управления стендом (1) и системы сбора данных B+SMultidata | |
| ||
Рис. 9. Статическая характеристика ПГР: 1 – экспериментальная характеристика; 2 – расчетная характеристика | ||
3.2. Исследование динамических характеристик ПГР
Динамические нагрузочные характеристики ПГР определялись следующим образом. Шток ПГР перемещался по гармоническому закону с частотой и амплитудой в соответствии с таблицей 4. При этом замерялись сила на штоке и ход штока. Колебания штока проходили относительно статического положения 0,12 м.
На рис. П1 – П12 (см. Приложение) представлены динамические характеристики ПГР для различных частот и амплитуд колебаний штока при начальном положении штока 0,12 м, полученные экспериментально, в сравнении с расчетными характеристиками, полученными при тех же условиях нагружения.
Таблица 4
Параметры колебания штока ПГР
Амплитуда, мм | 30 | 15 | 10 |
Частота колебаний штока ПГР, Гц | 0,2 0,4 0,6 0,8 1 1,2 | 2 2,4 3 3,5 - - | 6 8 - - - - |
Проведенное сравнение расчетных и экспериментальных нагрузочных характеристик двухобъемной пневмогидравлической рессоры (рис. П1 – П12) позволяет сделать следующие выводы:
· максимальное расхождение графиков нагрузочных характеристик, полученных экспериментально и расчетным путем, не превышает 10 %, что свидетельствует о приемлемой точности расчетов по разработанной математической модели ПГР;
· разработанная математическая модель адекватно описывает процессы течения рабочей жидкости и сжатия газа в ПГР, о чем свидетельствует не только количественное, но и качественное (по форме кривых) совпадение графиков нагрузочных характеристик, полученных экспериментально и расчетным путем.
3.3. Исследование пневмогидравлической рессоры на нагрев
Для оценки тепловой нагруженности ПГР были проведены испытания на нагрев. Нагружение рессоры осуществлялось периодической нагрузкой с амплитудой 30 мм и частотой 1 Гц. На рис. 10 представлен мультиметр с термопарой, используемые для измерения температуры блока пневмоцилиндров ПГР. Цель этих испытаний – исследование влияния нагрева ПГР на ее динамические характеристики. Во время испытаний фиксировалась температура большого пневмоцилиндра ПГР через каждые 30 с. После нагрева ПГР периодическим нагружением на 28°С (с 30 до 58°С) были получены динамические характеристики ПГР (рис. 11 – 13).

Рис. 10. Прибор для изменения температуры ПГР
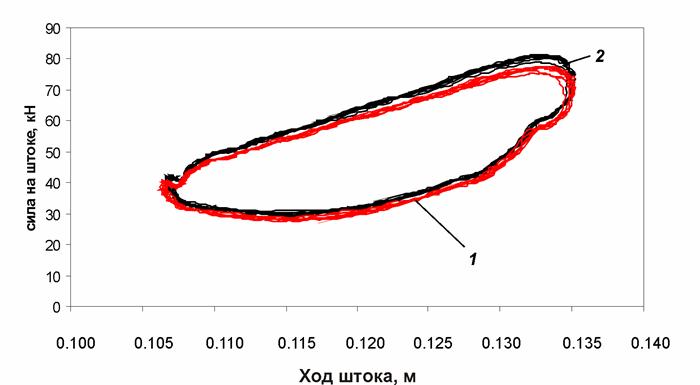
Рис. 11. Динамическая характеристика ПГР при частоте 3,5 Гц и амплитуде 15 мм для разных температур: 1 – температура 30°С; 2 – температура 58°С
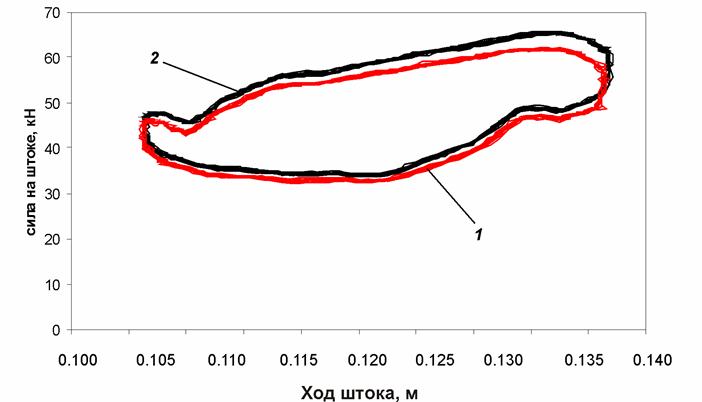
Рис. 12. Динамическая характеристика ПГР при частоте 6 Гц и амплитуде 10 мм для разных температур: 1 – температура 30°С; 2 – температура 58°С
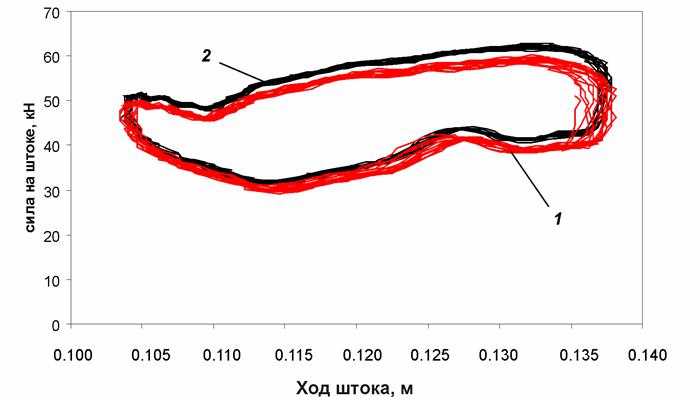
Рис. 13. Динамическая характеристика ПГР при частоте 8 Гц и амплитуде 10 мм для разных температур: 1 – температура 30°С; 2 – температура 58°С
Анализ динамических характеристик, представленных на рис. 11 – 13 позволяет сделать вывод, что нагрев в рабочей области температур практически не оказывает влияние на динамические характеристики ПГР. Таким образом, соответствующее допущение, принятое при разработке математических моделей пневмогидравлических устройств подвески МКМ, является правомерным.
Заключение
Разработана математическая модель двухобъемной пневмогидравлической рессоры подвески многоосных колесных машин, учитывающая динамику внутренних процессов, протекающих в ПГР. Модель может быть использована при исследовании методами имитационного моделирования управляемых систем подрессоривания МКМ.
Проведенное сравнение расчетных и экспериментальных нагрузочных характеристик двухобъемной пневмогидравлической рессоры свидетельствует приемлемой точности расчетов (ошибка не более 10 %) по разработанной математической модели ПГР. Разработанная математическая модель адекватно описывает процессы течения рабочей жидкости и сжатия газа в ПГР, о чем свидетельствует не только количественное, но и качественное (по форме кривых) совпадение графиков нагрузочных характеристик, полученных экспериментально и расчетным путем.
Показано, что нагрев пневмогидравлической рессоры в рабочей области температур практически не влияет на вид ее динамических нагрузочных характеристик. Соответствующее допущение, принятое при разработке математических моделей пневмогидравлических устройств подвески МКМ, является правомерным.
Список литературы
1. Певзнер Я.М. О выборе соотношений параметров передней и задней подвесок автомобиля // Автомобильная промышленность.- 1977.- N1. - С. 20-22.
2. Белоусов Б.Н., Попов С.Д. Колесные транспортные средства особо большой грузоподъемности. Конструкция. Теория. Расчет / Под общ. ред. Б.Н.Белоусова. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2006. – 728 с.
3. Смирнов А.А. Математическое моделирование пневмогидравлических устройств систем подрессоривания транспортных средств / Дисс… кандидата технических наук. – М.: МГТУ им. Н.Э.Баумана, 1999. – 179 с.
4. Расчет и проектирование строительных и дорожных машин на ЭВМ / Е. Ю. Малиновский, Л. Б. Зарецкий, Ю. Г. Беренгард, М. М. Гайцгори и др. Под ред. Е. Ю. Малиновского. – М.: Машиностроение, 1980. – 216 с.
5. Автоматизированное проектирование машиностроительного гидропривода / И. И. Бажин, Ю. Г. Беренгард, М. М. Гайцгори и др. Под общей ред. С. А. Ермакова. – М.: Машиностроение, 1988. – 312 с.
6. Абрамов Е.И., Колесниченко К.А., Маслов В.Т. Элементы гидропривода (справочник). – Киев: «Техника», 1977. – 320 с.
7. Бартенев Г.М., Лаврентьев В.В. Трение и износ полимеров. – Л.: Изд-во «Химия», 1972. - 240 с.
8. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ.- М.: Машиностроение, 1977. - 526 с.
9. Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. – М.: Машиностроение, 1987. – 232 с.
10. Башта Т.М. Гидропривод и гидропневмоавтоматика. Учеб. для вузов. – М.: Машиностроение, 1972. – 242 с.
Приложение
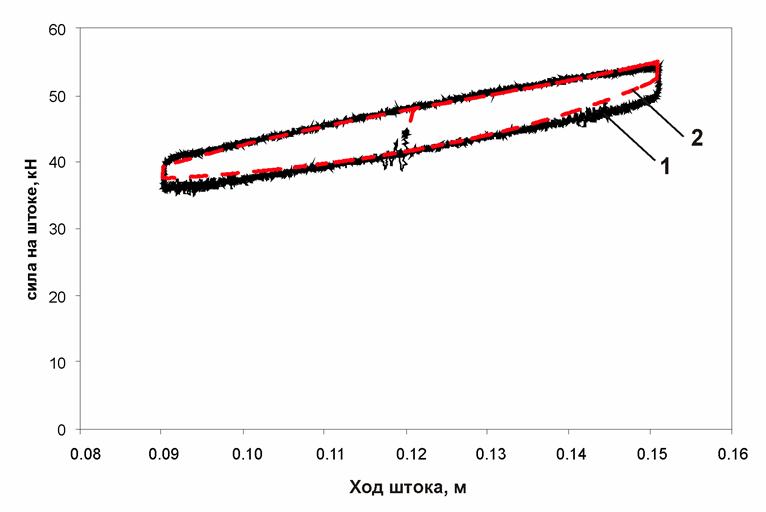
Рис. П1. Динамическая характеристика ПГР (частота 0,2 Гц; амплитуда 30 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
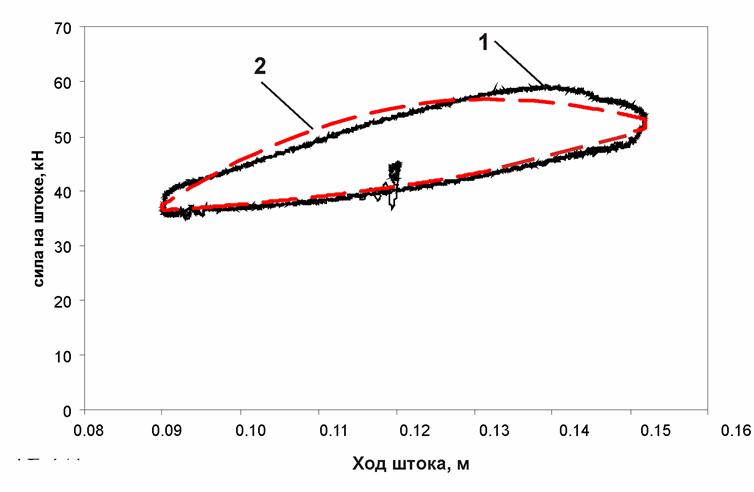
Рис. П2. Динамическая характеристика ПГР (частота 0,4 Гц; амплитуда 30 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
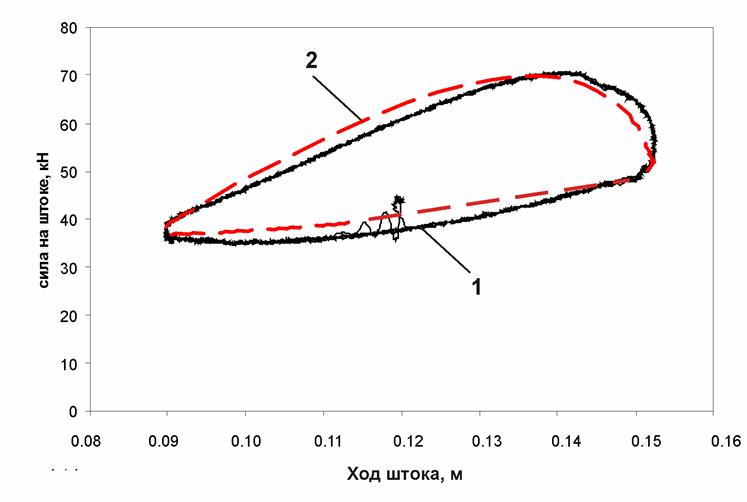
Рис. П3. Динамическая характеристика ПГР (частота 0,6 Гц; амплитуда 30 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
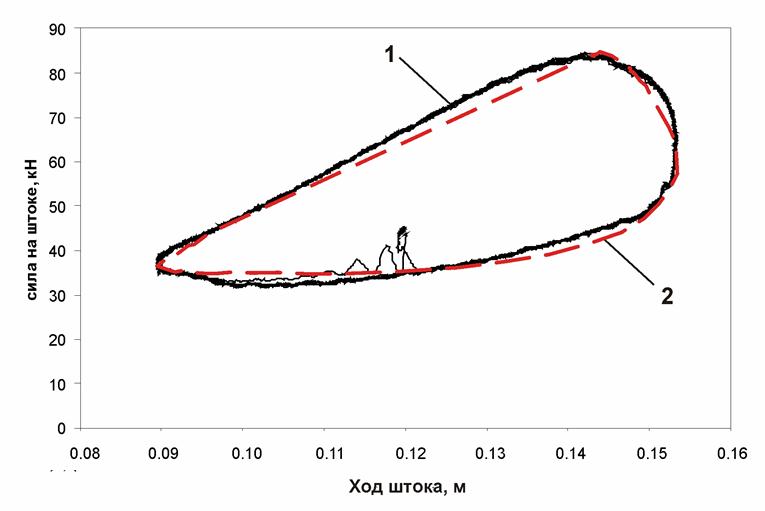
Рис. П4. Динамическая характеристика ПГР (частота 0,8 Гц; амплитуда 30 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
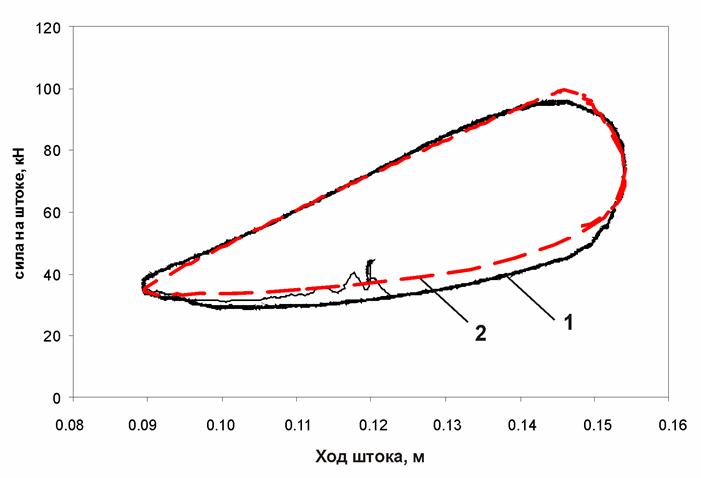
Рис. П5. Динамическая характеристика ПГР (частота 1 Гц; амплитуда 30 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
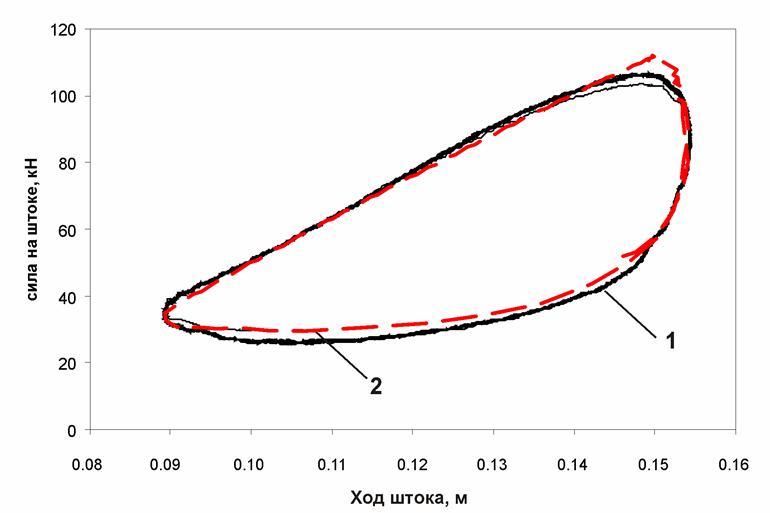
Рис. П6. Динамическая характеристика ПГР (частота 1,2 Гц; амплитуда 30 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
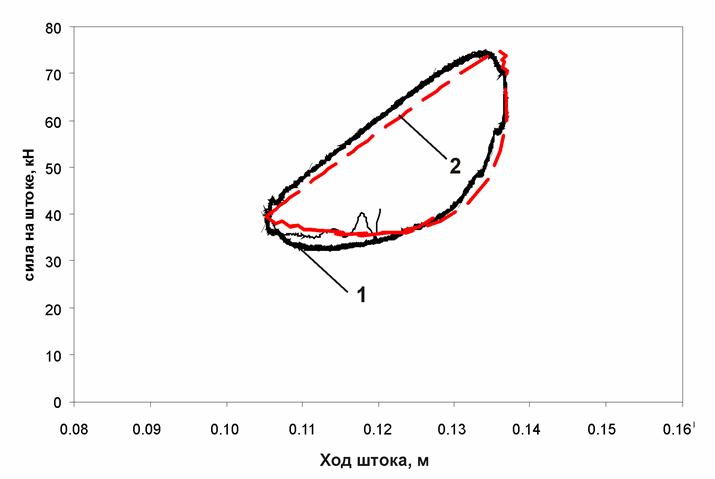
Рис. П7. Динамическая характеристика ПГР ( частота 2 Гц; амплитуда 15 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
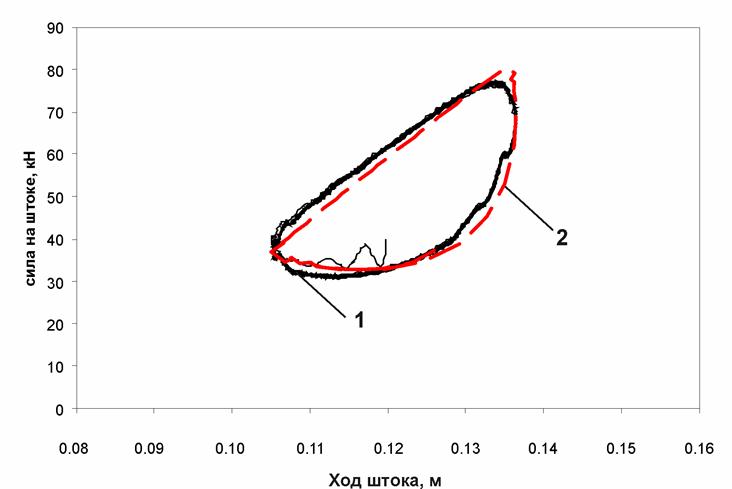
Рис. П8. Динамическая характеристика ПГР (частота 2,4 Гц; амплитуда 15 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
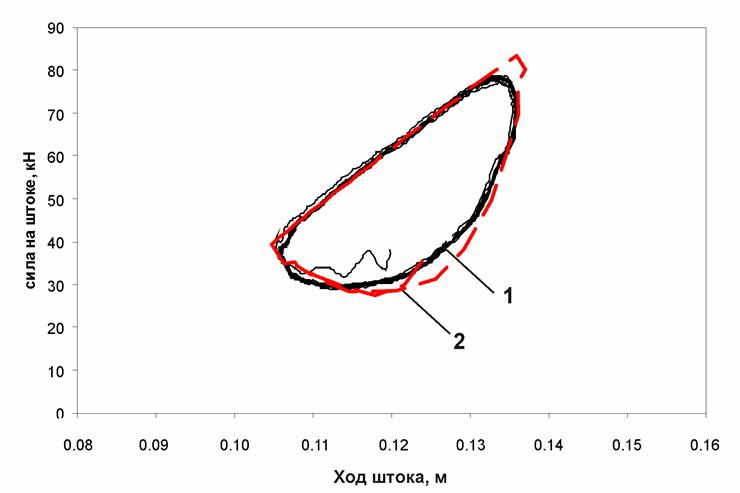
Рис. П9. Динамическая характеристика ПГР (частота 3 Гц; амплитуда 15 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика

Рис. П10. Динамическая характеристика ПГР (частота 3,5 Гц; амплитуда 15 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
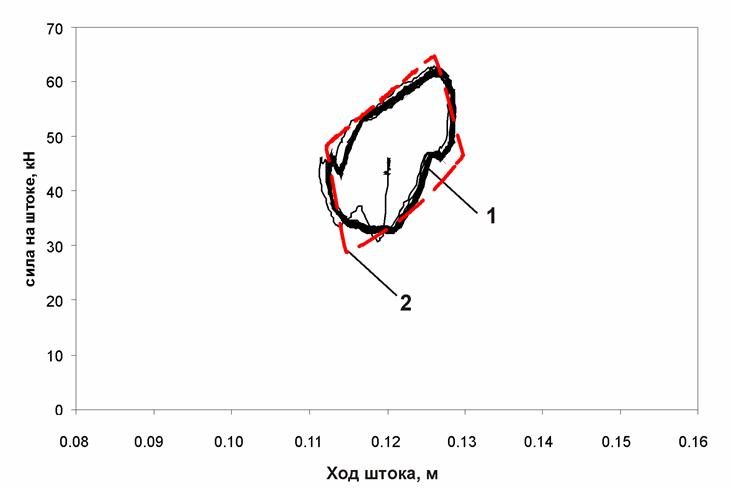
Рис. П11. Динамическая характеристика ПГР (частота 6 Гц; амплитуда 10 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
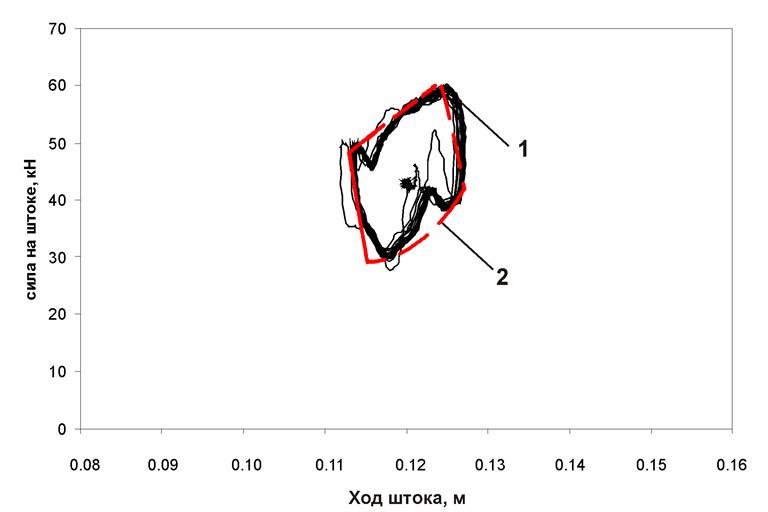
Рис. П12. Динамическая характеристика ПГР (частота 8 Гц; амплитуда 10 мм):
1 – экспериментальная характеристика; 2 – расчетная характеристика
Публикации с ключевыми словами: пневмогидравлическая рессора, упругая характеристика подвески, демпфирующая характеристика подвески, стендовые испытания
Публикации со словами: пневмогидравлическая рессора, упругая характеристика подвески, демпфирующая характеристика подвески, стендовые испытания
Смотри также:
- 77-30569/346660 Методика расчета характеристик пневмогидравлической управляемой подвески с двухуровневым демпфированием многоосных колесных машин
- Разработка адаптивного закона релейного управления трехуровневым демпфированием упруго-демпфирующих элементов подвески многоосных колесных машин
- 77-30569/293578 Методика подбора характеристик управляемой подвески с двумя уровнями демпфирования многоосных колесных машин
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||