научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 621.865.8-8
МГТУ им. Н.Э.Баумана
boshlyakov@mail.ru
ВВЕДЕНИЕ
В настоящее время является актуальной задача создания компактных безредукторных высокоточных мехатронных модулей. Например, в астрономии, в космических исследованиях, где требуется точная ориентировка по весьма малым объектам (звездам); в робототехнических комплексах, в особенности мобильных, для решения задач сканирования, ориентации и стабилизации датчиков информационных каналов [1] и т.п.
Представляется перспективным построение таких модулей на основе пьезоэлектрических двигателей, т.к. они обладают уникальной совокупностью положительных свойств, а именно:
Ø отсутствие люфта;
Ø потенциально может обеспечить высокую точность;
Ø эффект самоторможения (удержание момента на валу при отсутствии питающего напряжения);
Ø высокий удельный номинальный момент (как правило, больший, чем у электромагнитного двигателя того же объема);
Ø высокая надежность;
Ø обладает высоким быстродействием;
Ø отсутствие излучаемых полей;
Ø возможность миниатюризации.
Применение пьезоэлектрических двигателей вращения в следящих системах затрудняется сложностью управления ими. Пьезодвигатель с точки зрения управления представляет собой нелинейный объект. Причиной этому являются нелинейности пьезокерамики, наиболее существенные из которых – зависимость ее свойств от температуры и пьезоэлектрический гистерезис [2]. Отсутствие достаточно полной математической модели, описывающей поведение двигателя, затрудняет синтез регуляторов классическими методами теории управления. В работе [3] показана возможность использования инверсного нейросетевого регулятора для управления пьезодвигателем. Однако, настройка такого регулятора довольно сложный и трудоемкий процесс, не позволяющий менять весовые коэффициенты нейросети в процессе работы мехатронного модуля. Целью данной работы является построение адаптивного нейросетевого регулятора для управления пьезоэлектрическим двигателем вращения, обеспечивающего подстройку коэффициентов регулятора в функционирующей системе.
Основная идея предлагаемого подхода заключается в том, что в цепь ошибки вводится адаптивный регулятор, построенный на базе нейросети (рис. 1).

Рис. 1. Структура системы управления
Весовые коэффициенты сети настраиваются адаптивным регулятором в соответствии с принятым критерием качества без этапа предварительного обучения и только при наличии ошибки в системе. Как только ошибка в системе становится меньше допустимой, то корректировка весов прекращается. Корректировка весов выполняется лишь эпизодически, что обеспечивает высокоточную отработку мехатронным модулем быстротекущих сигналов.
СИНТЕЗ АДАПТИВНОГО РЕГУЛЯТОРА
За основу адаптивного регулятора (выделен пунктиром на рис. 2) был взят самонастраивающийся нейросетевой регулятор, предложенный в работе [4].

Рис. 2. Структура адаптивного регулятора.
Как показало моделирование, трех нейронов и двух производных ошибки управления достаточно для реализации адекватной обратной связи. Структурная схема нейросети представлена на рис. 3, где приняты следующие обозначения:
yr– уставка;
ey – ошибка;
u – сигнал управления;
y – регулируемая величина;
wi,j и vj – весовые коэффициенты;
hj – значение активационной функции нейрона.

Рис. 3. Структура нейросети
Сигнал управления u(t) формируется в следующем виде
 ,
,
 ,
,
где  .
.
Введем минимизируемый критерий качества управления
 ,
,
![]() ,
,
где время t полагается дискретным (шаг постоянный).
АЛГОРИТМ КОРРЕКТИРОВКИ ВЕСОВ
Для минимизации критерия будем использовать метод обратного распространения ошибки, для этого нам необходимо будет вычислить градиент функции E(t)
 .
.
Выражения для частных производных функции E(t) имеют вид

![]()
 ,
,

![]()
 ,
,
где xi –i-й вход нейросети.
В результате дифференцирования появляется частная производная ![]() , которую можно рассматривать как некий «эквивалентный коэффициент усиления» [4]. В дальнейшем мы вернемся к ней. На основе приведенных выше выражений выведем правила для корректировки весовых коэффициентов нейросети
, которую можно рассматривать как некий «эквивалентный коэффициент усиления» [4]. В дальнейшем мы вернемся к ней. На основе приведенных выше выражений выведем правила для корректировки весовых коэффициентов нейросети
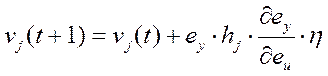 ,
,
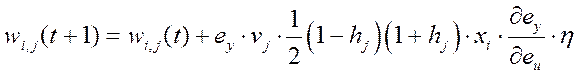 ,
,
где ![]() - коэффициент, влияющий на величину шага изменения весовых коэффициентов, т.е. на скорость обучения (learningrate).
- коэффициент, влияющий на величину шага изменения весовых коэффициентов, т.е. на скорость обучения (learningrate).
Данный метод замечателен своей простотой, но на пути к его применению возникает препятствие в виде указанной выше частной производной ![]() , так как в общем случае она неизвестна. Однако, достаточно знать её знак, поскольку амплитуда может быть учтена коэффициентом скорости обучения
, так как в общем случае она неизвестна. Однако, достаточно знать её знак, поскольку амплитуда может быть учтена коэффициентом скорости обучения ![]() при условии, что
при условии, что
 .
.
Кроме того, знак можно определить путем простого эксперимента – подачи на вход системы ступенчатой функции. Предположение о том, что знак этой частной производной для данной конкретной системы остается постоянным в окрестности рабочей точки, не является строгим, но выполняется на практике в большинстве случаев. В наихудшем случае можно реализовать оценку знака «на лету» в процессе работы системы управления. Таким образом правила корректировки весов нейросети принимают вид
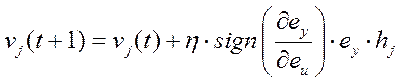 ,
,
 .
.
Схема алгоритма работы адаптивного регулятора представлен на рис. 4.
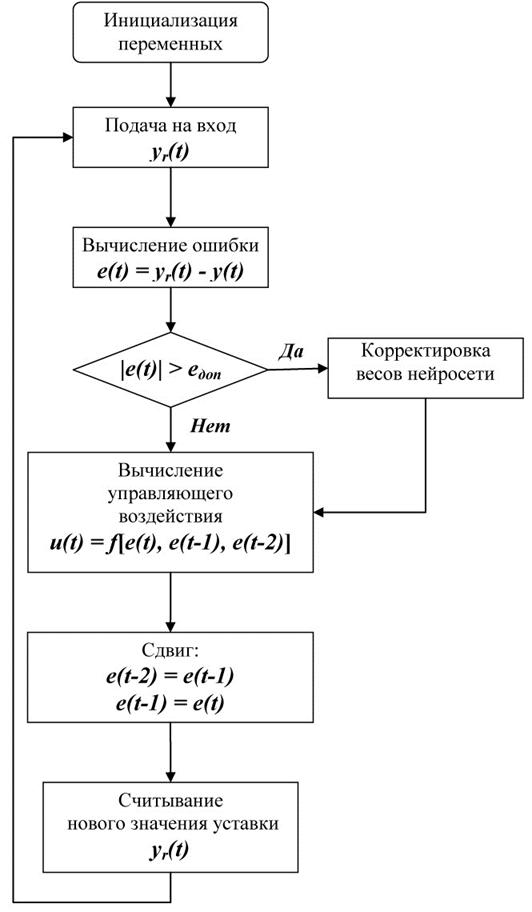
Рис. 4. Схема алгоритма работы адаптивного регулятора
МОДЕЛИРОВАНИЕ
Моделирование работы системы управления проводилось с помощью математического пакета MATLAB. В начале была произведена первичная настройка адаптивного регулятора по реакции системы на заранее приготовленный тестовый сигнал. Затем подавались различные сигналы.
1) Ступенчатое воздействие (рис. 5). Переходный процесс имеет колебательный характер, перерегулирование – не более 9 %, время вхождение сигнала в трубку 5%-го отклонения составляет 24 мс, установившаяся ошибка равна нулю.

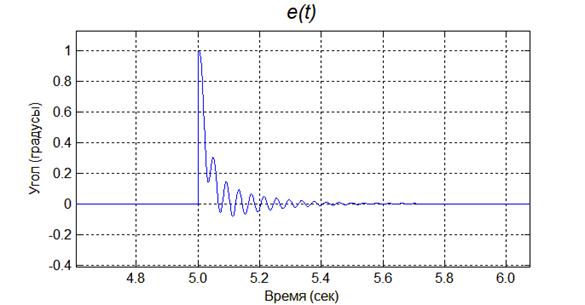
Рис. 5. Реакция на ступенчатое воздействие
2) Синусоидальное воздействие: частота 2 Гц; амплитуда 50 (рис. 6). Динамическая ошибка не превышает 11 минут, нелинейные искажения отсутствуют, временной сдвиг равен 2,5 мс.

Рис. 6. Реакция на синусоидальное воздействие (частота 2 Гц; амплитуда 50)
3) Синусоидальное воздействие: частота 20 Гц; амплитуда 50 (рис. 7). Динамическая ошибка не превышает 10, нелинейные искажения отсутствуют, временной сдвиг равен 3 мс.
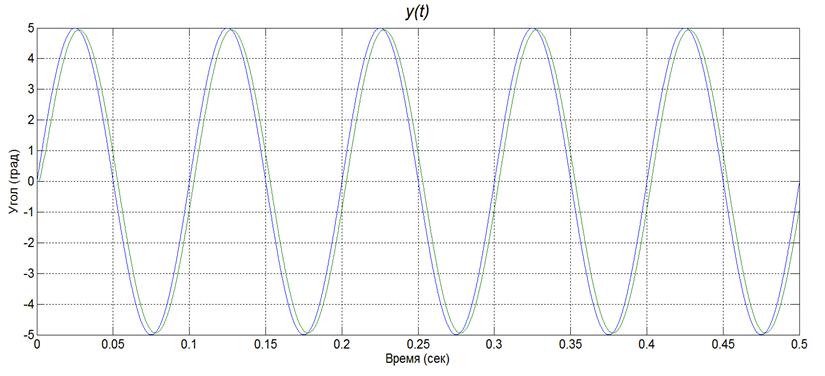
Рис. 7. Реакция на синусоидальное воздействие (частота 20 Гц; амплитуда 50)
4) Ломаный сигнал (рис. 8). Колебательности практически нет, на линейных участках динамическая ошибка не превышает 0,30.


Рис. 8. Реакция на ломаный сигнал
5) Комбинированное воздействие (рис. 9). При ступенчатых перепадах возникают колебания, идентичные тем, что наблюдаются при реакции на ступенчатое воздействие. На линейном участке динамическая ошибка не превышает 1,2 мин. На следующем за ним горизонтальном участке ошибка равна нулю.


Рис. 9. Реакция на комбинированное воздействие
6) Ступенчатый сигнал (рис. 10): высота одной ступеньки составляет 10,длина горизонтального участка ступеньки произвольна в пределах от 10 до 25 мс. На горизонтальных участках в установившемся режиме ошибка не превышает 0,010 и со временем стремится к нулю, а после 12 мс становится меньше 30”.

Рис. 10. Ступенчатый сигнал
АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
Приведенные выше результаты были получены при частоте замыкания контура обратной связи равной 10 кГц. В процессе моделирования возник ряд проблем.
1) Перед включением системы управления матрицы весовых коэффициентов должны быть инициализированы ненулевыми начальными значениями.
2) Коэффициент η можно сделать либо постоянным, либо реализовать адаптивное изменение его значения в зависимости от величины текущей ошибки. Моделирование показало, что введение адаптивного изменения скорости обучения резко снижает устойчивость процесса управления, поэтому был принят первый вариант. Значение коэффициента подбиралось эмпирически.
3) Реализованный в данной работе метод корректировки весовых коэффициентов нейросети имеет ограниченную скорость сходимости, поэтому чем выше частота сигнала управления, тем больше динамическая ошибка системы управления. Это легко заметить на графиках реакции системы на синусоидальное входное воздействие с частотой 2 Гц и 20 Гц – динамическая ошибка возрастает в 6 раз.
4) Адаптивный регулятор достаточно хорошо отрабатывает постоянные входные воздействия. Есть небольшая колебательность, но она быстро затухает, а перерегулирование не превышает 9 %. Кроме того, через 24 мс, ошибка становится меньше 5 %. Однако в случае линейных входных сигналов наблюдается постоянная динамическая ошибка, обусловленная временным запаздыванием.
5) Моделирование показало, что знак частной производной ![]()
не остается постоянным даже в окрестности рабочей точки, поэтому было реализовано определение знака в процессе работы системы управления. Для этого было использовано разностное приближение
 .
.
ЗАКЛЮЧЕНИЕ
При выполнении данной работы были получены следующие результаты.
Синтезирован адаптивный нейросетевой регулятор для управления пьезоэлектрическим двигателем вращения.
Проведено моделирование работы всей системы, которое показало целесообразность предложенного подхода построения системы управления.
В заключение стоит отметить, что качество процесса управления можно значительно улучшить, применив более быстрый метод оптимизации весовых коэффициентов нейросети.
Список литературы
1. Бордаченков А.В., Бошляков А.А., Рубцов И.В. Быстродействующий привод сканирования и стабилизации изображения в системах технического зрения мобильных робототехнических комплексов // Интеллектуальные робототехнические системы-2001: Материалы науч. молод. школы. Таганрог: Изд-во ТРГУ, 2001, с.138-139.
2. Рассадкин Ю. И., Бошляков А.А., Лебедев А. Ю. Выбор метода управления лепестковым пьезоэлектрическим двигателем вращения для ориентации и стабилизации датчиков систем технического зрения //Электротехнические системы и комплексы: Межвузовский сб. науч. тр. - (Магнитогорск). 2007. Вып.14, c.287-293.
3. Борисов В.В., Бошляков А.А., Иванов Д.А., Лебедев А.Ю. Реализация нейросетевого регулятора для управления пьезоэлектрическим двигателем // Известия ЮФУ, Технические науки. 2010. №12(113), c.190 - 195.
4. Ponce N., Behar A., Hernandez O., Sitar R., “Neural Networks for Self-tuning Control Systems”, Czech Technical University Publishing House, 2004. Acta Polytechnica Vol. 44, No. 1/2004, p. 49-52.
Публикации с ключевыми словами: система управления, мехатронный модуль, пьезоэлектрический двигатель вращения, нейросетевой регулятор
Публикации со словами: система управления, мехатронный модуль, пьезоэлектрический двигатель вращения, нейросетевой регулятор
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



