научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 620.18: 669-419:621.771, 548.1
МГТУ им. Н.Э. Баумана
МГУ им. М.В. Ломоносова
1. Введение
Эффекты гигантского магнитного момента и спинового стекла наблюдаются в металлических сплавах, находящихся в кристаллическом, аморфном [1–3] или квазикристаллическом [4] состояниях. Общепринятым объяснением происхождения гигантского магнитного момента считается косвенное обменное взаимодействие магнитных ионов благодаря поляризации электронов проводимости (взаимодействие Рудермана-Киттеля-Касуя-Иосида, РККИ). Однако, обнаруженная в работе [4] зависимость температуры замерзания спинового стекла и величины гигантского магнитного момента от симметрии квазикристалла Al-Mn (икосаэдрической или декагональной) заставляет предположить, что гигантский момент обусловлен не только особенностями электронного строения сплава, но и особенностями ближнего атомного окружения. На основании такого предположения авторы [5] в рамках теории функционала плотности выполнили расчеты электронной структуры и магнитного момента тригональных и тетраэдрических кластеров, из которых ранее была собрана иерархическая структура квазикристалла [6]. Строение этих кластеров представляет собой икосаэдрическую оболочку из ионов алюминия, внутри которой располагаются либо треугольники, либо тетраэдры, составленные из ионов 3d-переходного металла (Mn или Со). Тригональная либо тетраэдрическая симметрия кластеров обусловлена пересечением трех либо четырех икосаэдров алюминия, а координаты ионов, образующих кластер, взяты из эксперимента, поскольку кластеры являются фрагментами кристаллических структур некоторых интерметаллидов систем Al-3d-переходный металл. Согласно проведенным расчетам оказалось, что в кластерах, образованных алюминием и кобальтом, магнитный момент кластера равен нулю, а в кластерах Al-Mn магнитный момент треугольника из ионов марганца равен приблизительно 3 моментам изолированного иона марганца, а момент марганцевого тетраэдра равен 12 магнитным моментам изолированного иона марганца. Этим явлением в работе [5] и был объяснен гигантский магнитный момента квазикристаллов Al-Mn, наблюдавшийся в [4]. Несмотря на то, что в кристаллических твердых растворах типа Pd-Mn, Cu-Mn и многих других гигантский момент наблюдается в однофазной области твердого раствора на основе благородного металла, естественно предположить, что и в этом случае появление эффектов гигантского магнитного момента и спинового стекла может быть обусловлено существованием кластеров магнитного иона в номинально однофазном твердом растворе. Аномалии физических свойств в однофазном (по рентгеновским данным) твердом растворе давно известны, достаточно указать на аномалию электросопротивления в сплаве Ni-20%Сr , в сплавах Fe-Al, Ni-Mo и др. [7, 8], а также отклонение концентрационной зависимости избыточного электросопротивления твердого раствора от квадратичного закона (правила Линде) [9]. Гинье показал [10], что полностью однородных твердых растворов не существует, поскольку однородное распределение в обратном пространстве интенсивности рассеяния Лауэ не наблюдалось никогда.
Поэтому в настоящей работе была поставлена задача расчета электронного строения и величины магнитного момента в ГЦК-твердых растворах на основе палладия и меди, в узлах кристаллической решетки которого размещены не только единичные ионы растворенного марганца, но и скопления двух, трех, или четырех ионов марганца, т.е. гантели, треугольники или тетраэдры. Выбор систем Pd-Mn и Cu-Mn обусловлен большим числом исследований явлений спинового стекла и гигантского магнитного момента в них.
2. Методика расчетов и модель кластеров примеси в твердом растворе
Первопринципные расчеты в данной работе выполнены на основе теории функционала электронной плотности (density functional theory, DFT) [11]. Для учёта обменно-корреляционных эффектов в этом методе обычно используется приближение локальной плотности (local density approximation, LDA) [12], которое с высокой точностью позволяет описать равновесный объём и стабильную кристаллическую структуру чистых элементов или их соединений. LDA использует обменно-корреляционную энергию однородного электронного газа в каждой точке системы, игнорируя неоднородность реальной плотности заряда. Для неоднородной плотности заряда обменно-корреляционная энергия может значительно отклоняться от случая однородного электронного газа. Отклонение может быть выражено через градиент и пространственную производную высшего порядка от полной плотности заряда. Приближение обобщенного градиента (generalized gradient approximation, GGA) [13] использует градиент зарядовой плотности для учёта этого отклонения, что позволяет добиться большей точности расчётов, поэтому оно было использовано в расчётах.
В данном компьютерном эксперименте был использован современный метод расчёта электронной структуры — PAW метод (projectoraugmented-wave) [14], т. к. он совместно с приближением GGA позволяет получить наиболее точные результаты, но требует больше вычислительных затрат по сравнению с приближением LDAдля обменно-корелляционного функционала.
Эффекты спинового стекла и гигантского магнитного момента в системах Pd-Mnи Cu-Mnсоответствует областям однородного твердого раствора замещения. В работе предполагается, что атомы растворённого марганца распределяются по узлам решётки растворителя не равномерно, а образуют скопления (кластеры), содержащие 2, 3 или 4 атома (иона).
В соответствии с геометрией ГЦК решётки 2, 3 или 4 иона марганца образуют гантель, треугольник и тетраэдр. Во всех случаях ребро кластера совпадает с направлениями <110> ГЦК решетки. Длина ребра (гантели, треугольника, тетраэдра) соответствует либо ближайшему соседству ионов марганца, либо упорядоченному чередованию с ионами растворителя через один или два иона Mnили Cu, всего получается 9 вариантов размещения магнитных ионов марганца (рис. 1).
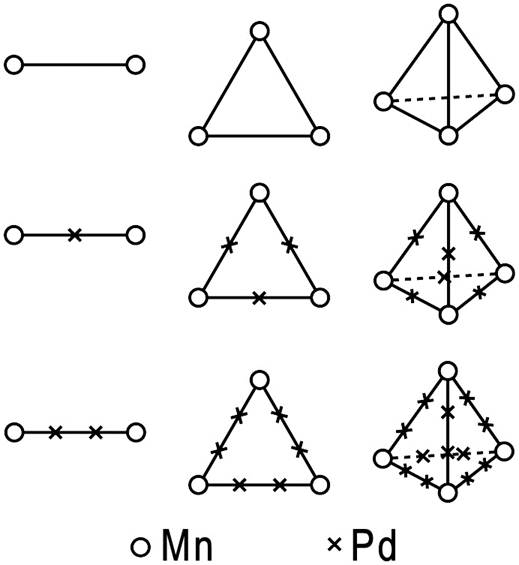
Рис. 1. Девять конфигураций кластеров марганца в палладии.
При замещении палладия атомами марганца возникают нескомпенсированные силы межатомного взаимодействия. Для нахождения энергетического минимума системы требуется переместить атомы таким образом, чтобы уравновесить эти силы. Для этого в наших компьютерных экспериментах проводилась оптимизация формы и объёма элементарной ячейки.
Расчёт проводили в суперячейке палладия размерами 3х3х3 элементарных ячейки (108 атомов), что позволяет получить концентрацию марганца в палладии примерно 1–4 ат. %. Расчеты проводили для объемного случая (bulk calculations), т.е. считали, что исследуемый объём значительно удалён от поверхности. При таком допущении можно исключить из рассмотрения поверхностные эффекты.
Поскольку имеющиеся в нашем распоряжении вычислительные мощности не позволяют провести расчёт ячейки большей, чем 3х3х3, то максимально большим объектом, который можно построить в данной суперячейке является тетраэдр в котором марганец располагается через 2 атома палладия.
Этот тетраэдр с ребром Mn-Pd-Pd-Mn заполняет весь объём суперячейки, т.е. образуется сверхструктура (рис. 2):
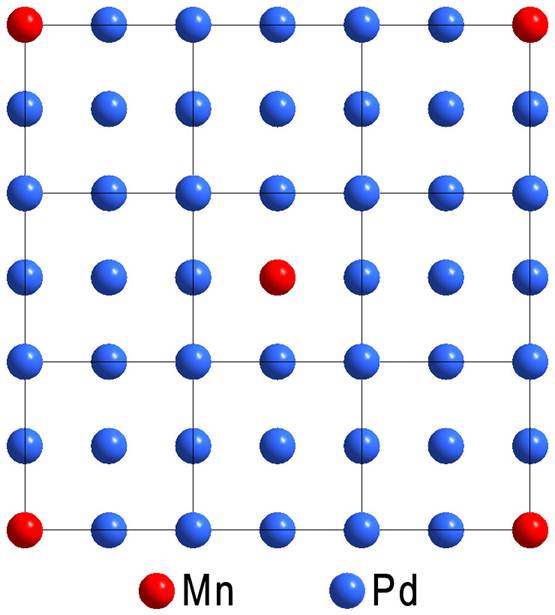
Рис. 2. Упорядоченный твёрдый раствор марганца в палладии. Суперячейка с утроенным периодом решётки.
3. Результаты и обсуждение
Расчетное распределение электронной плотности в решетке Pd для единичного иона марганца и тетраэдрического кластера марганца в разных сечениях кубической решетки показано на рис. 3 и 4 соответственно. Расчеты свободной энергии (при 0 К) показали, что во всех случаях образование кластеров марганца стабилизирует систему по сравнению с растворением единичного иона (рис. 5). Интересно отметить, что даже при некотором удалении ионов примеси энергетический выигрыш от образования кластеров примерно одинаков и для непосредственного контакта между ионами марганца, и при образовании связей Mn-Pd-Mn и Mn-Pd-Pd-Mn, причем для всех конфигураций — гантельной, треугольной и тетраэдрической.

Рис. 3. Распределение электронной плотности для единичного иона Mnв решетке Pd в сечениях соответственно (100) и (111).

Рис. 4. Распределение электронной плотности в решетке Pd с тетраэдрическим кластером Mnв плоскости (111) тетраэдра с ребрами Mn-Pd-Mn(а) и в плоскости (100) с ребром тетраэдра Mn-Pd-Mn (б).
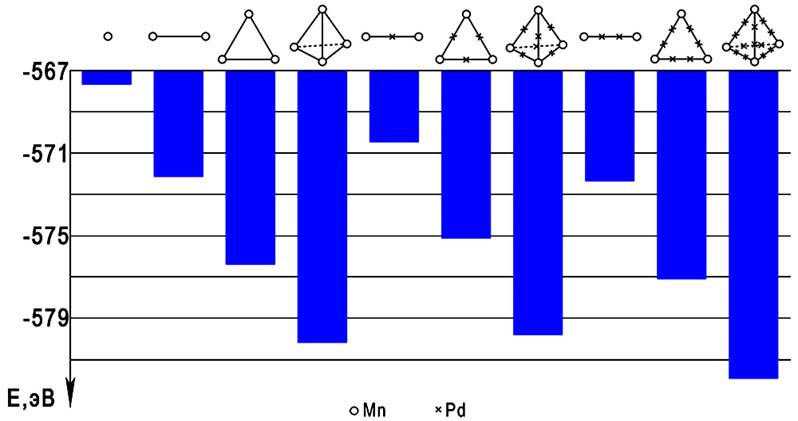
Рис. 5. Свободная энергия E для твердого раствора Pd–Mn с различными кластерами.
Согласно многочисленным экспериментальным и теоретическим исследованиям, в спиновых стеклах системы Pd-Mn обменное взаимодействие Mn-Mn в первой координационной сфере носит антиферромагнитный характер, а взаимодействие в следующих координационных сферах является ферромагнитным [15–18]. Это хорошо согласуется с результатами наших расчетов магнитного момента, которые показаны на рис. 6.
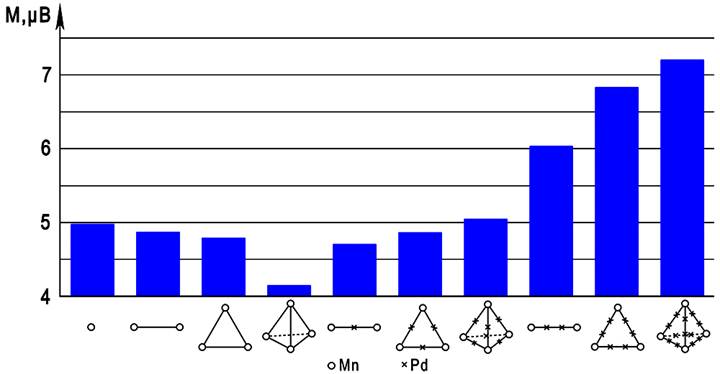
Рис. 6. Величина магнитного момента (M, в магнетонах Бора) на ион марганца для различных кластеров в твердом растворе системы Pd–Mn.
Как видно, эффект гигантского магнитного момента наблюдается уже для единичного иона марганца в узле решетки палладия (для изолированного иона марганца магнитный момент составляет 1,3 µВ). Кластеры с ближайшим соседством ионов марганца подавляют суммарный момент, и этот эффект усиливается с увеличением числа ионов марганца в кластере: момент снижается от 5 до 4,2 µВ. Это проявление антиферромагнитного взаимодействия между ионами марганца. При удалении ионов марганца в кластере величина магнитного момента постепенно растет и уже в тетраэдрическом кластере, построенном на связях Mn-Pd-Mn величина магнитного момента такая же, как у единичного иона марганца. Интересно, что в кластерах на связях Mn-Pd-Pd-Mn эффект гигантского момента усиливается, и у тетраэдрического кластера, построенного на связях Mn-Pd-Pd-Mn, величина момента на ион марганца уже значительно превышает момент для изолированного иона примеси, достигая величины 7,2 µВ, т.е. 5,5 момента единичного изолированного иона марганца. Возможно, это явление той же природы, что и полученный нами в работе [5] момент в 12 моментов единичного иона для тетраэдрического кластера марганца, заключенного в икосаэдрическую оболочку алюминия. По абсолютной величине (7,2 µВ) полученный нами результат также хорошо согласуется с экспериментальной величиной гигантского момента в сплавах Pd-Mn (7,8 µВ) [15, 19]. Зависимость магнитного момента от атомных конфигураций позволяет также понять наблюдаемое снижение намагниченности спинового стекла Pd-Mn c увеличением концентрации марганца [15]. В целом наблюдаемая на рис.6 тенденция изменения гигантского момента соответствует опубликованной фазовой магнитной диаграмме для растворов Pd-Mn [20].
На рис. 7, 8 показаны результаты аналогичных расчетов свободной энергии и магнитного момента, выполненных для растворов Cu-Mn, проявляющих эффект спинового стекла. Как и в системе Pd-Mn, образование кластеров стабилизирует систему (рис. 7), однако в отношении магнитного момента тенденция иная (рис. 8). Изолированный ион марганца имеет повышенный магнитный момент, что соответствует РККИ-поляризации s-полосы меди [2]. В кластерах Mn-Mn магнитный момент постепенно понижается с увеличением числа ионов марганца в кластере вследствие прямого антиферромагнитного взаимодействия Mn-Mn, как и в системе Pd-Mn. Однако в кластерах с косвенными контактами Mn-Cu-Mn магнитный слабо снижается, а в кластерах с более далекими контактами Mn-Cu-Cu-Mn момент остается постоянным на уровне изолированного иона марганца. Такое поведение хорошо согласуется с современными представлениями о растворах Cu-Mn как смеси ферромагнитного и антиферромагнитного упорядочения [2, 18]. В кластерах с косвенными контактами магнитных ионов ферромагнитное взаимодействие через поляризацию электронов проводимости частично или полностью компенсирует прямое антиферромагнитное взаимодействие, и магнитный момент остается примерно на уровне изолированного иона марганца. В работе [18] отмечается, что в упорядоченном сплаве Cu3Mn (по типу L12, или Cu3Au) спины взаимодействую ферромагнитно, а рассмотренные нами кластеры вида Mn-Сu-Mn как раз соответствуют этому типу упорядочения.
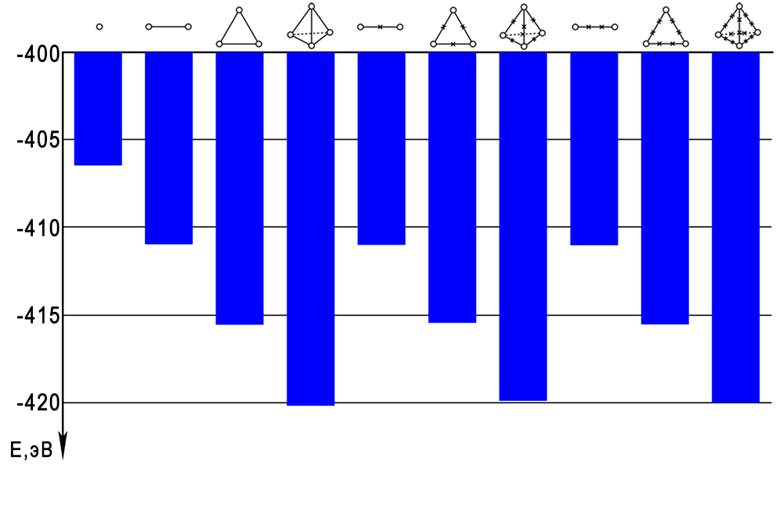
Рис. 7. Свободная энергия E для твердого раствора Cu-Mnс различными кластерами.
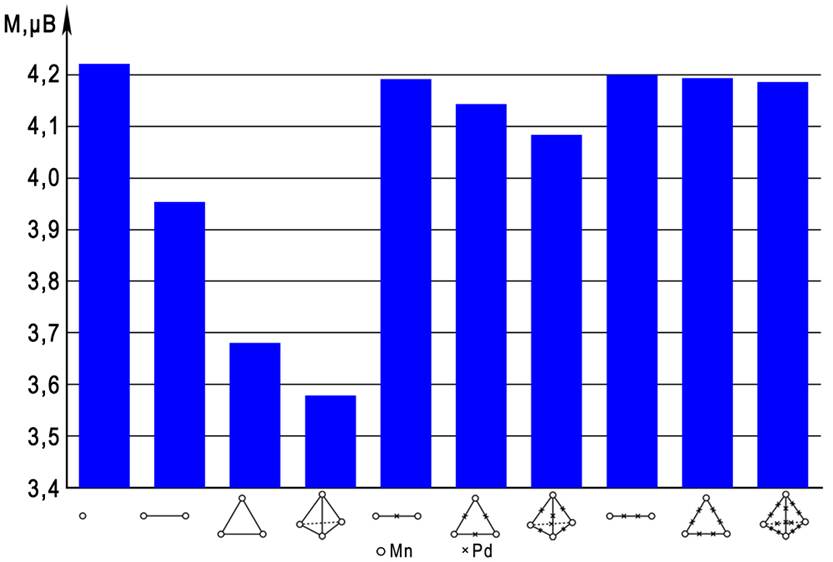
Рис. 8. Величина магнитного момента (M, в магнетонах Бора) на ион марганца для различных кластеров в твердых растворах Cu–Mn.
По мнению авторов работы [19] происхождение эффектов спинового стекла в твердых растворах Cu-Mn и Pd-Mn имеет разную физическую природу. В таких системах, как Cu-Mn и Au-Fe (их считают типичными спиновыми стеклами) поведение спинового стекла есть следствие пространственных осцилляций взаимодействия РККИ, а в системе Pd-Mn это же поведение вызвано конкуренцией между непосредственным антиферромагнитным взаимодействием и косвенным ферромагнитным. Во всяком случае, результаты выполненных расчетов отражают выявленную в многочисленных экспериментах разницу в магнитном поведении растворов Pd-Mn и Cu-Mn при однотипном атомном строении (одна и та же кристаллическая решетка и одинаковые кластеры магнитной примеси).
Таким образом, проведенные расчеты и их согласие с экспериментальными данными показывают, что явления гигантского магнитного момента обусловлены не только деталями электронной структуры, но и структурой атомного ближнего порядка. Атомные неоднородности (кластеры) в несколько атомов оказались энергетически выгодными, так что твердый раствор с подобными аномалиями магнетизма можно считать неоднородным твердым раствором, и даже назвать коллоидным раствором. В цитированной выше работе [19] на основе измерений концентрационных зависимостей спонтанной намагниченности, электросопротивления и удельной теплоемкости твердых растворов Pd-Mn в области концентраций до 10 ат. % Mn была рассчитана доля атомов марганца в кластерах и в виде единичных (изолированных) ионов. Оказалось, что доля изолированных ионов снижается с ростом содержания марганца в растворе. Это также согласуется с нашими расчетами.
Тонкую структуру ближнего порядка в твердых растворах наблюдали давно, в том числе предлагались модели распределения атомов растворенного компонента в виде тетраэдров [21]. Наблюдение зон Гинье-Престона с октаэдрической огранкой в сплаве Al-5%Ag [22] хотя и относится уже к зонной стадии распада твердого раствора, но также может служить свидетельством в пользу развиваемых в настоящей работе представлений о неоднородностях твердого раствора. По-видимому, октаэдрические зоны Гинье-Престона – некоторая поздняя стадия объединения тетраэдрических кластеров в твердом растворе. Автор обзора [23], обобщая многочисленные данные, указывает, что в распадающихся сплавах выше кривой растворимости возможно образование в матрице областей ближнего порядка типа расслоения (кластеров), Такие кластеры и были обнаружены при высокотемпературном исследовании сплавов Al-Cu [24].
4. Выводы
1. В рамках теории функционала плотности выполнены расчеты электронной плотности и магнитного момента твердых растворов Pd-Mn и Cu-Mn, проявляющих поведение спинового стекла и эффект гигантского магнитного момента, и содержащих кластеры с числом ионов марганца в кластере от 2 до 4 (гантель, треугольник или тетраэдр). Ионы марганца располагались в узлах кристаллической решетки палладия или меди, и находились либо в непосредственном контакте между собой (Mn-Mn), либо образовывали ребра Mn-Pd-Mn, Mn-Pd-Pd-Mn или Mn-Cu-Mn, Mn-Cu-Cu-Mn.
2. Рассчитанные значения свободной энергии при всех конфигурациях кластеров соответствуют их стабилизации в обеих системах, глубина энергетического минимума увеличивается с ростом числа ионов марганца в кластере, поэтому однофазные твердые растворы в системах Pd-Mn и Cu-Mn можно рассматривать как твердые коллоидные растворы.
3. Эффект гигантского магнитного момента существует уже для единичного иона марганца решетках Pd или Cu (соответственно 5 или 4,2 µВ на ион марганца), в случае непосредственных контактов Mn-Mn этот эффект подавляется при увеличении числа магнитных ионов в кластере ( в сплаве Pd-Mn4,2 µВ на ион марганца в тетраэдре), а в случае контактов через ион палладия усиливается при увеличении числа ионов марганца в кластере (7,2 µВ на ион марганца в тетраэдре с ребрами Mn-Pd-Pd-Mn). В случае контактов через ион меди магнитный момент остается постоянным на уровне момента единичного иона марганца в решетке меди.
4. Результаты расчетов магнитного моментов в растворах Pd-Mn и Cu-Mn с кластерами соответствуют литературным данным для спиновых стекол Pd-Mn и Cu-Mn (антиферромагнитное взаимодействие между ионами марганца в первой координационной сфере и ферромагнитное взаимодействие в следующих сферах). В целом можно считать, что явление гигантского магнитного момента определяется не только особенностями электронной структуры, но и локальным атомным порядком.
Благодарности
Работа выполнена в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007–2013 годы», ГК № 16.523.11.3010 по теме «Создание комплекса вакуумных и ионно-вакуумных технологий химико-термической обработки деталей машин с получением наноструктурированного состояния диффузионных слоёв», а также при финансовой поддержке РФФИ (проекты 10–02–00602, 11–02–00296). Компьютерные вычисления выполнены на суперкомпьютерах Межведомственного Суперкомпьютерного Центра (МСЦ), Москва, РФ.
Литература
- Mydosh I.A. Spin Glasses, an experimental introduction. London: Taylor and Francis, 1993.
- Binder K., Yong A.P. Spin glasses: Experimental facts, theoretical concepts, and open questions // Rev. Mod. Phys. 1986. V.58. #4. P.801-976.
- Fisher K.H., Hertz J.A. Spin Glasses. England: Cambridge University, Cambridge, 1991. 418 p.
- Yang D.P., Hines W.A., Clark W.G., Machado F.L.A., Azevedo L.A., Giessen B.C., Quan M.X. Magnetization study of the I-Al80Mn20 and T-Al78Mn22 quasicrystalline phases // Journal of Magnetism and Magnetic Materials. 1992. V.109. P.1-6.
- Kraposhin V.S., Bazhanov D.I., Bocharov P.V. On the origin of the giant magnetic moment of the Al-Mn quasicrystals // Eur. Phys. J. Web of Conferences 15, 03012 (2011) DOI: 10.1051/epjconf/20111503012.
- Kraposhin V. S., Talis A.L., Lam Ha Thanh, Dubois J.-M. Model for the transformation оf an icosahedral phase into a B2 crystalline phase // J. Phys.: Condens. Matter. 2008. V.20. P.235215 (8ppм.).
- Лившиц Б.Г., Равдель М.П. // Доклады АН СССР, 1953.- Т.93.-С.1033.
- Warlimont H., Aubauer H. // Z. Metallkunde, 1973.- H.64.- S.484.
- Linde J.O. // Helvecia Physica Acta, 1968.-V.41. –P.1007-1015.
- Неоднородные металлические твердые растворы/А. Гинье-М.: Издательство иностранной литературы, 1962.- 158 с. [ Guinier A. Heterogeneities in solid solutions // Solid State Physics, Ed. by F. Seitz, D. Turnbull, 1959- Academic Press, New York, London].
- Hohenberg P., Kohn W. Inhomogeneous Electron Gas // Phys. Rev. 136 864 (1964).
- Kohn W., Sham L. Self-Consistent Equations Including Exchange and Correlation Effects // Phys. Rev. 140 1133 (1965).
- Perdew J.P., Burke S., Ernzerhof M. Generalized Gradient Approximation Made Simple // Phys. Rev. Lett. B 77 3865 (1996).
- Blochl P.E. Projector augmented-wave method // Phys. Rev. B 24 17953 (1994)
- Guy C. N. , Howarth W. Spin glass behavior of the FCC solid solutions Pd-Mn // Proc. 2nd Int. Symp. on Amorphous Magnetism, P.137-144. (New York, Plenum Press, 1976).
- Star W. M. , Foner S. , McNiff, Jr. E. J. Giant mompent and ferromagnetism in dilute Pd(Mn) alloys // Physical Review, 1975. V. 12. P.2690-2709.
- Nieuwenhuys G.J. Magnetic behaviour of cobalt, iron and manganese dissolved in palladium // Adv. in Physics, 24(1975) 515-591.
- Coles B. R., Jamieson H., Tajlor R. H. , Tari A . Limited ferromagnetism and other magnetic properties of Pd-Mn alloys // J . Phys. F: Metal Phys. 1975. Vol. 5. P.565-574.
- Nieuwenhuys G. J., Verbeek B.H. On the magnetic ordering in palladium-manganese dilute alloys // J. Phys. F: Metal Phys. 1977.- V.7.-P.1497-1503.
- B.R. Coles, H.I. Jamieson, R.H. Tajlor, Tari A. Limited ferromagnetism and other magnetic properties of Pd-Mn alloys // J . Phys. F: Metal Phys. 1975. -V. 5.- P.565-574.
- Borie B., Sparks C. J. The short-range structure of copper-16 at. % aluminum // Acta Crystallographica, 1964. -V.17.-P. 827-835.
- Alexander K.B., Legoues F.K., Aaronson H.I., Laughlin D.E. Faceting of GP zones in an Al-Ag alloy // Acta Metallurgica, 1984.-V. 32.- P. 2241-2249.
- Чуистов К.В. Начальные стадии распада пересыщенных твердых растворов. I. Зоны и комплексы // Металлофизика и новейшие технологии, 1995.-Т.17. -№4. – С.7-24.
- Matsubara E., Cohen J.B. Local atomic arrangements in the solid solution Al-1.7 at.% Cu, at 793 K // Acta Metallurgica, 1983.-V. 31.- P. 2129-2135.
Публикации с ключевыми словами: нанокластеры, твердые растворы, электронная структура, спиновые стекла, теория функционала плотности
Публикации со словами: нанокластеры, твердые растворы, электронная структура, спиновые стекла, теория функционала плотности
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



