научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 51-7 530.1 531 14
Самостоятельный исследователь


1. Введение
Кони нуждаются в движении каждый день [1]. Поэтому при больших конюшнях обычно имеется прогулочный круг, используемый для выгула коней, если погода неблагоприятна для дальних прогулок. Также на этом кругу берут первые уроки верховой езды начинающие наездники. Излишне объяснять почему, это и так ясно, время от времени конь на кругу должен менять направление вращения. При этом конь сходит с окружности и по некоторой кривой направляется к центру круга. Затем по симметричной кривой он возвращается на окружность в точке, диаметрально противоположной точке схода, и продолжает движение по окружности уже в другом направлении.
Один хороший друг автора, большой любитель верховой езды и восточной мудрости, однажды обратил внимание, что в целом траектория коня при описанном маневре делит круг на две части, похожие на хорошо известные в древней китайской премудрости фигуры Инь-Ян [2, 3, 4]. Качественно совершенно ясно поведение коня при маневре смены направления вращения. Ничего другого, кроме кривой типа Инь-Ян при этом получиться не может. Однако, упомянутый друг автора предложил подвести математическую базу под это явление. В результате появилась на свет настоящая работа. Исходная предпосылка работы состоит в том, что конь выбирает после многократных повторений маневра оптимальную, наименее утомительную траекторию.
В данной работе предлагается математическая модель утомляемости коня и производится вариационный вывод уравнений движения [5]с помощью этой модели. Уравнения решаются в общем интегральном виде и затем численно с учетом граничных условий типа Инь-Ян в точках выхода на окружность (или схода с нее) и в центре круга. Результаты представлены в графическом виде вместе с их обсуждением.
2. Вариационная постановка задачи и вывод
уравнений движения
От чего устает конь? Он устает даже, если ничего не делает, как и прочие живые существа. Просто со временем все нуждаются во сне. Здесь мы пренебрегаем этой усталостью. Мы полагаем, что конь бежит и устает от бега. Он устает и тогда, когда движется по прямой с постоянной скоростью. Но кони выносливы, они способны долго скакать без видимой усталости. Поэтому эта не та усталость, которая нас здесь интересует. Нас интересует усталость от движения с переменной скоростью, т.е. с ускорениеми, как продольным, меняющим скорость по величине, так и поперечным, сообщающим траектории кривизну. В общем случае, как свидетельствует преизбыточный опыт наездников, эти два вида ускорения утомляют коня в разной степени.
Наша задача здесь найти оптимальную, наименее утомительную траекторию бегущего коня при заданных граничных условиях, а именно его начальных и конечных положений и скоростей. С этой целью определим интегрально утомление как функционал от вектора скорости ![]() , записываемый в виде
, записываемый в виде
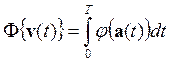 , (1)
, (1)
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,  ,
,
![]()
где ![]() – вектор ускорения,
– вектор ускорения, ![]() и
и ![]() – его продольная и поперечная компоненты,
– его продольная и поперечная компоненты, ![]() и
и ![]() – коэффициенты утомления от соответственно продольного и поперечного ускорений,
– коэффициенты утомления от соответственно продольного и поперечного ускорений, ![]() – угол вектора скорости, отсчитываемый от оси х , T– полное время движения для половины траектории. Для определенности здесь и ниже рассматривается половина траектории, начиная от центра до точки выхода на окружность. Другая половина, после начала маневра получается преобразованием центральной симметрии
– угол вектора скорости, отсчитываемый от оси х , T– полное время движения для половины траектории. Для определенности здесь и ниже рассматривается половина траектории, начиная от центра до точки выхода на окружность. Другая половина, после начала маневра получается преобразованием центральной симметрии ![]() ,
, ![]() , где
, где ![]() – текущий радиус-вектор,
– текущий радиус-вектор, ![]()
Следуя стандартной процедуре [5], вычисляя вариационные производные [6]от функционала (1) по компонентам скорости и приравнивая их нулю по условию экстремума, получаем после несколько громоздких вычислений уравнения движения в виде
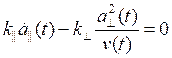 , (2)
, (2)
 . (3)
. (3)
При выводе ур-ний (2) и (3) , как обычно, вариации скорости на концах временного интервала полагаются равными нулю.
Из ур-ний (2) и (3) легко получаем
![]()
и далее после интегрирования
 , (4)
, (4)
где ![]() – интеграл движения, равный половине утомления на единицу времени (см (1)), т.е. если уж утомляться, то лучше это делать равномерно по времени. Величину
– интеграл движения, равный половине утомления на единицу времени (см (1)), т.е. если уж утомляться, то лучше это делать равномерно по времени. Величину ![]() не следует путать с кинетической энергией, мы используем это обозначение лишь как дань традиции.
не следует путать с кинетической энергией, мы используем это обозначение лишь как дань традиции.
Ур-ния (3) и (4) удобно решать в частности для нашей задачи Инь-Ян, перейдя в полярную систему координат в пространстве скоростей, т.е. вместо искомых функций ![]() и
и ![]() решать уравнения для абсолютной величины скорости
решать уравнения для абсолютной величины скорости ![]() и угла
и угла ![]() (см (1)). Опять, опуская громоздкие выкладки, приведем получаемые ур-ния. Ур-ние (4) примает вид
(см (1)). Опять, опуская громоздкие выкладки, приведем получаемые ур-ния. Ур-ние (4) примает вид
 , (5)
, (5)
а вместо (3) приходим к ур-нию
![]() ,
,
которое легко интегрируется
![]() , (6)
, (6)
где ![]() еще один интеграл движения, аналогичный моменту количества движения, но не являющийся таковым. Как и в случае традиционной задачи движения в поле центральных сил, наличие интеграла движения
еще один интеграл движения, аналогичный моменту количества движения, но не являющийся таковым. Как и в случае традиционной задачи движения в поле центральных сил, наличие интеграла движения ![]() вытекает из симметрии системы итносительно сдвигов по времени, а интеграл движения
вытекает из симметрии системы итносительно сдвигов по времени, а интеграл движения ![]() обусловлен симметрией системы относительно поворотов на произвольный угол (теорема Нётр [7]).
обусловлен симметрией системы относительно поворотов на произвольный угол (теорема Нётр [7]).
Ур-ния (5) и (6) составляют систему двух диф-ных ур-ний первого порядка. Для ее решения требуется два граничных условия. Запишем требуемые граничные условия для точки выхода на окружность в виде
![]() , (7)
, (7)
![]() ,
,
где ![]() – постоянная скорость, с которой конь совершает движение по окружности по или против часовой стрелки, а время
– постоянная скорость, с которой конь совершает движение по окружности по или против часовой стрелки, а время ![]() определено в (1). Для полярной системы координат равенства (7) дают
определено в (1). Для полярной системы координат равенства (7) дают
![]() , (8)
, (8)
 .
.
Начальные условия для ![]() и
и ![]() пока остаются неопределенными. Эти величины будут определены ниже из начальных и конечных условий для координат
пока остаются неопределенными. Эти величины будут определены ниже из начальных и конечных условий для координат ![]() и
и ![]() .
.
Прежде, чем перейти к решению ура-ний (5) и (6), удобно переписать их вместе с граничными условиями (8) в безразмерном виде, используя упомянутый выше парметр ![]() и еще один параметр – радиус беговой дорожки
и еще один параметр – радиус беговой дорожки ![]() . Запишем переход к безразмерным величинам в виде следующей цепочки равенств:
. Запишем переход к безразмерным величинам в виде следующей цепочки равенств:
 ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
 ,
,
 ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно безразмерные время, координаты, вектор скорости, скрость по модулю и перенормированные в соответствии с их размерностями (см. (4) и (6)) интегралы движения
соответственно безразмерные время, координаты, вектор скорости, скрость по модулю и перенормированные в соответствии с их размерностями (см. (4) и (6)) интегралы движения ![]() и
и ![]() .
.
Ур-ния (5) и (6) в безразмерных единицах принимают вид
 , (9)
, (9)
![]() , (10)
, (10)
где вместо коэффициентов утомления ![]() и
и ![]() введен один параметр – их отношение
введен один параметр – их отношение ![]() . Во избежание увеличения обозначений под точкой теперь будет пониматься дифференцирование по безразмерному времени
. Во избежание увеличения обозначений под точкой теперь будет пониматься дифференцирование по безразмерному времени ![]() , т.е. например,
, т.е. например, ![]() .
.
Вместо граничных условий (8) теперь имеем
![]() , (11)
, (11)
 ,
,
где под ![]() понимается теперь безразмерное полное время движения до выхода на окружность.
понимается теперь безразмерное полное время движения до выхода на окружность.
3. Решение задачи Инь-Ян
Исключая ![]() из ур-ний (9) и (10), получаем ур-ние только для
из ур-ний (9) и (10), получаем ур-ние только для ![]() вида
вида
 , (12)
, (12)
которое легко решается
![]() , (13)
, (13)
где ![]() – постоянная интегрирования, определяемая условием
– постоянная интегрирования, определяемая условием ![]() . В момент времени
. В момент времени ![]() убывание скорости меняется на ее возрастание. Ниже из графика траектории будет видно, что этот момент прохождения через некую вершину траектории, с чем связано ее обозначение индексом 'а' (apex– вершина). Соответствующая минимальная скорость определяется из (12) и равна
убывание скорости меняется на ее возрастание. Ниже из графика траектории будет видно, что этот момент прохождения через некую вершину траектории, с чем связано ее обозначение индексом 'а' (apex– вершина). Соответствующая минимальная скорость определяется из (12) и равна
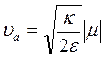 . (14)
. (14)
Начальная скорость в центре беговой окружности с помощью (13) записывается как
![]() . (15)
. (15)
После подстановки ![]() из (13) в (10), угол
из (13) в (10), угол ![]() находится простым интегрированием
находится простым интегрированием
![]() , (16)
, (16)
где ![]() – начальный угол, а переменная часть
– начальный угол, а переменная часть ![]() получается в виде
получается в виде
 ,
, ![]() . (17)
. (17)
Для рассматриваемой ветви траектории угол ![]() ожидается убывающим. Поэтому ниже полагается
ожидается убывающим. Поэтому ниже полагается ![]() и соответственно
и соответственно ![]() .
.
Граничные условия (11) приобретают вид ур-ний
![]() , (18)
, (18)
 .
.
Значения четырех величин ![]() ,
, ![]() (или
(или ![]() ),
), ![]() и
и ![]() , из коих в силу (18) только две независимы, остаются пока неизвестными. Дополнительные два уравнения определяются из граничных условий для координат
, из коих в силу (18) только две независимы, остаются пока неизвестными. Дополнительные два уравнения определяются из граничных условий для координат ![]() и
и ![]() . Запишем их в виде
. Запишем их в виде
![]() ,
, ![]() . (19)
. (19)
Выпишем выражения для ![]() и
и ![]() , получаемые простым интегрированием проекций скорости
, получаемые простым интегрированием проекций скорости
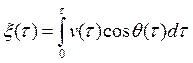 ,
, ![]() , (20)
, (20)
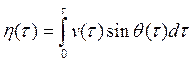
![]() ,
,
где функции ![]() и
и ![]() определены соответственно в (13) и (16) . Далее определим две функции
определены соответственно в (13) и (16) . Далее определим две функции
 ,
, 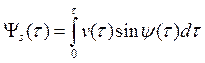 , (20)
, (20)
где функция ![]() определена в (17). С их помощью граничные условия (19) можно переписать в удобном для численого решения виде
определена в (17). С их помощью граничные условия (19) можно переписать в удобном для численого решения виде
![]() , (21)
, (21)
![]() .
.
Таким образом четыре ур-ния (18) и (21) определяют все четыре параметра, а именно ![]() ,
, ![]() (или
(или ![]() ),
), ![]() и
и ![]() как функции полного времени
как функции полного времени ![]() , задаваемое, естественно, всадником. Знание численных значений в свою очередь позволяет численно рассчитать траекторию и поведение всех интересующиех нас величин во времени и построить соответствующие графики.
, задаваемое, естественно, всадником. Знание численных значений в свою очередь позволяет численно рассчитать траекторию и поведение всех интересующиех нас величин во времени и построить соответствующие графики.
Функции (20) в общем случае, за исключением случая ![]() , не вычисляются аналитически. Поэтому система ур-ний (18) и (21) была решена численно методом Ньютона [8]с помощью компьютерной программы в системе технического программирования Matlab[9]. Результаты этого решения для различных значений свободных параметров
, не вычисляются аналитически. Поэтому система ур-ний (18) и (21) была решена численно методом Ньютона [8]с помощью компьютерной программы в системе технического программирования Matlab[9]. Результаты этого решения для различных значений свободных параметров ![]() и
и ![]() представлены графически в следующем разделе.
представлены графически в следующем разделе.
4. Графическое представление решения и его обсуждение
Кони, как и люди, бывают разные, юркие, средние и не очень поворотливые. Кроме того всадник может предоставить коню самому решать, как оптимально совершить маневр, или вынудить его сделать это в заданное время. Поэтому были рассмотрены и получены два множества траекторий.
В первом множестве изменяется параметр ![]() при одинаковом для всех траекторий значении радиуса кривизны на выходе на окружность
при одинаковом для всех траекторий значении радиуса кривизны на выходе на окружность ![]() , равным радиусу беговой дорожки, т.е. в безразмерных единицах равным 1. Этот тот случай, когда конь делает маневр свободно, без принуждения. Для каждой отдельной траектории вычисляется время
, равным радиусу беговой дорожки, т.е. в безразмерных единицах равным 1. Этот тот случай, когда конь делает маневр свободно, без принуждения. Для каждой отдельной траектории вычисляется время ![]() и значение
и значение ![]() (см. (12)), представленные ниже в Таб. 1.
(см. (12)), представленные ниже в Таб. 1.
Во втором множестве параметр ![]() держится постоянным для всех траекторий с принятым значением
держится постоянным для всех траекторий с принятым значением ![]() , а изменению подлежит радиус кривизны на выходе на окружность
, а изменению подлежит радиус кривизны на выходе на окружность ![]() (иначе траектория выйдет за беговую дорожку). В этом случае конь вынужден на входе и выходе скачком изменить радиус кривизны, чтобы совершить маневр за более кроткое время. Для этого множества время
(иначе траектория выйдет за беговую дорожку). В этом случае конь вынужден на входе и выходе скачком изменить радиус кривизны, чтобы совершить маневр за более кроткое время. Для этого множества время ![]() задается, а значение
задается, а значение ![]() и радиус кривизны
и радиус кривизны ![]() вычисляются. Эти данные представлены ниже в Таб. 2.
вычисляются. Эти данные представлены ниже в Таб. 2.
1. Первое множество решений, ![]() .
.
Траектории, явно имеющие вид фигур Инь-Ян, представлены на Рис. 1
Значения параметра ![]() на рис. 1 сверху вниз в правой половине равны: 0.2, 0.4, ..., 2.0. Каждая половина кривой с
на рис. 1 сверху вниз в правой половине равны: 0.2, 0.4, ..., 2.0. Каждая половина кривой с ![]() (центральная красная линия) – обыкновенная парабола, представляющая равноускоренное движение (подобно полету камня, брошенного под углом к горизонту).
(центральная красная линия) – обыкновенная парабола, представляющая равноускоренное движение (подобно полету камня, брошенного под углом к горизонту).

Рис. 1
Особый интерес представляют траектории с малыми значениями ![]() . Поэтому были расчитаны кривые, аналогичные кривым на рис. 1, с
. Поэтому были расчитаны кривые, аналогичные кривым на рис. 1, с ![]() 0.2, 0.18, ..., 0.02, а также исследован и найден предел
0.2, 0.18, ..., 0.02, а также исследован и найден предел![]() . Соответствующие траектории, включая
. Соответствующие траектории, включая ![]() , показаны на рис. 2. Также, как и на рис. 1, траектории следуют в порядке возрастания
, показаны на рис. 2. Также, как и на рис. 1, траектории следуют в порядке возрастания ![]() в правой половине окружности сверху вниз. Значения
в правой половине окружности сверху вниз. Значения ![]() не рассматривались как не имеющие отношения к реальности.
не рассматривались как не имеющие отношения к реальности.
На Рис. 3 показано поведение координат ![]() и
и ![]() во времени для значений
во времени для значений ![]() 0.0, 0.1, 0.2, 0.4, ..., 2.0 (в порядке убывания сверху вниз на левом рисунке, и снизу вверх на правом рисунке в его правой части). Здесь и ниже для удобства сравнения, т.е. чтобы конечные точки совпадали для всех кривых, используются приведенные времена, т.е. свой масштаб для каждой кривой с базовым периодом
0.0, 0.1, 0.2, 0.4, ..., 2.0 (в порядке убывания сверху вниз на левом рисунке, и снизу вверх на правом рисунке в его правой части). Здесь и ниже для удобства сравнения, т.е. чтобы конечные точки совпадали для всех кривых, используются приведенные времена, т.е. свой масштаб для каждой кривой с базовым периодом ![]() :
:
 ,
,
где ![]() – значение времени
– значение времени ![]() для данной кривой (см. Таб. 1). Выбор базового периода в виде
для данной кривой (см. Таб. 1). Выбор базового периода в виде ![]() , не имеет какого-либо специального значения. Просто траектория с
, не имеет какого-либо специального значения. Просто траектория с ![]() была при вычислениях первой.
была при вычислениях первой.
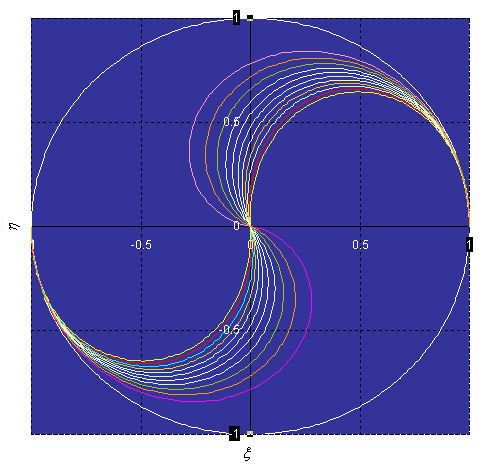
Рис. 2
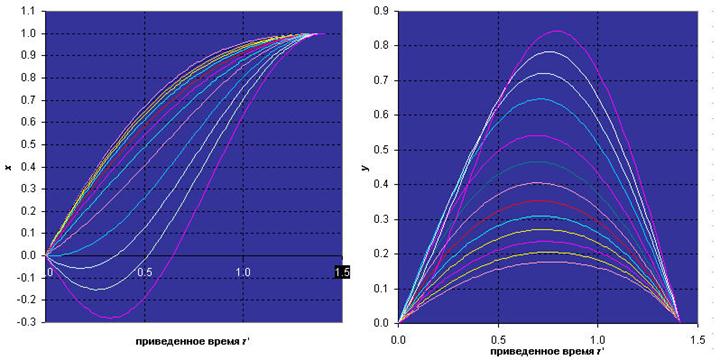
Рис. 3
На рис. 4 слева представлены графики поведения скорости по модулю для тех же значений ![]() 0.0, 0.1, 0.2, 0.4, ..., 2.0 в порядке убывания
0.0, 0.1, 0.2, 0.4, ..., 2.0 в порядке убывания ![]() сверху вниз вблизи начальной временной точки. Все линии, за исключением линии с
сверху вниз вблизи начальной временной точки. Все линии, за исключением линии с ![]() , являются отрезками гипербол, что вытекает из (13). Из этого выражения также следует, что в случае
, являются отрезками гипербол, что вытекает из (13). Из этого выражения также следует, что в случае![]() график претставляет собой прямую, как это видно на рис. 4 (вырожденная гипербола). Минимальные скорости при прохожднии вершин гипербол достигаются при
график претставляет собой прямую, как это видно на рис. 4 (вырожденная гипербола). Минимальные скорости при прохожднии вершин гипербол достигаются при ![]() .
.

Рис. 4
На рис. 4 справа показаны графики траекторий в пространстве скоростей для тех же значений ![]() в порядке возрастания
в порядке возрастания ![]() сверху слева направо. Красная прямая линия соответствует случаю
сверху слева направо. Красная прямая линия соответствует случаю ![]() – равноускоренное движение.
– равноускоренное движение.
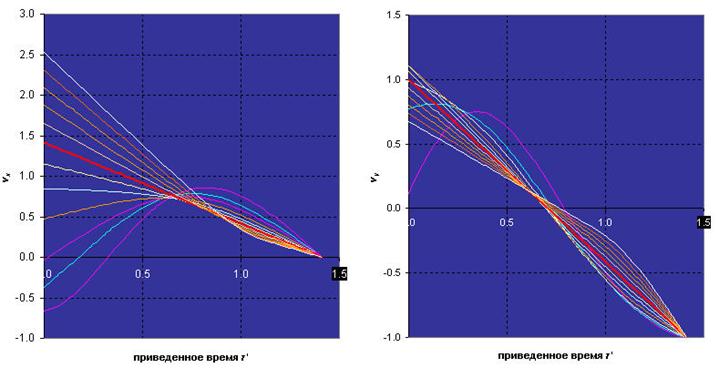
Рис. 5
На рис. 5 показано поведение проекций скоростей ![]() и
и ![]() во времени снова для значений
во времени снова для значений ![]() 0.0, 0.1, 0.2, 0.4, ..., 2.0 (в порядке убывания сверху вниз на левом рисунке вблизи начальной временной точки, и снизу вверх на правом рисунке в его средней части). Опять красная прямая линия соответствует случаю
0.0, 0.1, 0.2, 0.4, ..., 2.0 (в порядке убывания сверху вниз на левом рисунке вблизи начальной временной точки, и снизу вверх на правом рисунке в его средней части). Опять красная прямая линия соответствует случаю ![]() – равноускоренное движение.
– равноускоренное движение.
Полезно отметить, что время прохода через упомянутую выше вершину ![]() (см. (13)) принимает отрицательные значения в некоторой малой области значений
(см. (13)) принимает отрицательные значения в некоторой малой области значений ![]() около нуля, включая сам нуль, как это видно в частности для
около нуля, включая сам нуль, как это видно в частности для ![]() из Таб. 1. Поэтому собственно сам проход для таких значений
из Таб. 1. Поэтому собственно сам проход для таких значений ![]() оказывается вне приведенных рисунков временной зависимости, за их левыми краями, и модуль скорости монотонно возрастает на всей траектории.
оказывается вне приведенных рисунков временной зависимости, за их левыми краями, и модуль скорости монотонно возрастает на всей траектории.
Таблица 1
|
|
|
|
0.00 | 3.04450 | 0.01169 | -6.20421 |
0.04 | 2.71159 | 0.07086 | 0.23249 |
0.10 | 2.44193 | 0.16853 | 0.88859 |
0.20 | 2.17946 | 0.35312 | 1.07132 |
0.40 | 1.87734 | 0.80438 | 1.08678 |
0.60 | 1.68307 | 1.37735 | 1.04294 |
0.80 | 1.53566 | 2.09704 | 0.99257 |
1.00 | 1.41421 | 3.00000 | 0.94281 |
1.20 | 1.30901 | 4.13774 | 0.89478 |
1.40 | 1.21473 | 5.58320 | 0.84840 |
1.60 | 1.12808 | 7.44144 | 0.80329 |
1.80 | 1.04688 | 9.86756 | 0.75904 |
2.00 | 0.96954 | 13.09780 | 0.71520 |
1. Второе множество решений, ![]() .
.
По опыту наездников обычно поперечное ускорение на порядок меньше утомляет коня. С этим связан выбор значения ![]() . Траектории типа фигур Инь-Ян, представлены на Рис. 6. За исключением верхней и нижних кривых в правой части, остальные кривые вычислены для заданых
. Траектории типа фигур Инь-Ян, представлены на Рис. 6. За исключением верхней и нижних кривых в правой части, остальные кривые вычислены для заданых ![]() 1.2, 1.4, ..., 2.4 . На Рис. 6 они следуют в порядке возрастания снизу вверх в правой части. Каждая из них имеет свой радиус кривизны
1.2, 1.4, ..., 2.4 . На Рис. 6 они следуют в порядке возрастания снизу вверх в правой части. Каждая из них имеет свой радиус кривизны ![]() на выходе на окружность, как это видно из Таб. 2. Самая верхняя кривая на Рис. 6 имеет максимальный радиус кривизны
на выходе на окружность, как это видно из Таб. 2. Самая верхняя кривая на Рис. 6 имеет максимальный радиус кривизны ![]() и период
и период ![]() (см. Таб. 1). Эта линия присутствует также среди кривых первого множества на Рис. 1.
(см. Таб. 1). Эта линия присутствует также среди кривых первого множества на Рис. 1.
Как это выяснилось в процессе вычислений второе множество решений ограничено снизу предельным значением ![]() (см. Таб. 2). Ниже этого значения систем ур-ний (18) и (21) при данном значении
(см. Таб. 2). Ниже этого значения систем ур-ний (18) и (21) при данном значении ![]() не имеет вещественных решений. Предельная кривая также представлена на Рис. 6 – самая нижняя желтая линия. Как можно показать, критерием этого предела является величина
не имеет вещественных решений. Предельная кривая также представлена на Рис. 6 – самая нижняя желтая линия. Как можно показать, критерием этого предела является величина
![]() , (22)
, (22)
которая обращается в нуль на этом пределе (см. Таб. 2). Можно показать также, что равенство ![]() равносильно обращению в нуль продольной компоненты ускорения в точке выхода на окружность, т.е. в этой точке
равносильно обращению в нуль продольной компоненты ускорения в точке выхода на окружность, т.е. в этой точке ![]() .
.

Рис. 6
На рис. 7 показано поведение координат ![]() и
и ![]() во времени для значений
во времени для значений ![]() 2.44193,2.4, 2.2, ... , 1.2, 1.15528 (в порядке убывания сверху вниз на левом рисунке, и снизу вверх на правом рисунке в его правой части).
2.44193,2.4, 2.2, ... , 1.2, 1.15528 (в порядке убывания сверху вниз на левом рисунке, и снизу вверх на правом рисунке в его правой части).

Рис. 7
На рис. 8, аналогичном рис. 4, слева представлены графики поведения скорости. Опять все линии являются отрезками гипербол, и минимальные скорости при прохожднии вершин гипербол достигаются при ![]() . Полезно отметить, что, как это видно на этом рисунке, для предельной кривой вершина гиперболы совпадает с точкой выхода, т.е. для значения
. Полезно отметить, что, как это видно на этом рисунке, для предельной кривой вершина гиперболы совпадает с точкой выхода, т.е. для значения ![]() имеем
имеем ![]() .
.

Рис. 8
На рис. 8 справа показаны графики траекторий в пространстве скоростей, а на рис. 9 показано поведение проекций скоростей ![]() и
и ![]() во времени.
во времени.

Рис. 9
Обнаружение предельной траектории с ![]() явилось неожиданностью. Поначалу это трудно предвидеть, поскольку в (22) как
явилось неожиданностью. Поначалу это трудно предвидеть, поскольку в (22) как ![]() , так и
, так и ![]() подлежат вычислению. С наличием такой предельной траектории возникает вопрос: какова же все-таки оптимальная траектория, если требуемое время
подлежат вычислению. С наличием такой предельной траектории возникает вопрос: какова же все-таки оптимальная траектория, если требуемое время ![]() ? Такая траектория должна существовать. Возможный ответ: для
? Такая траектория должна существовать. Возможный ответ: для ![]() кроме скачков поперечного ускорения на входе (или выходе) должен быть еще такой скачок в какой-то промежуточный момент, один или несколько. Но это уже другая постановка, с другой более сложной системой уравнений нежели система (18) и (21). Эта задача здесь не решалась. Педлагаем ее заинтересованному читателю.
кроме скачков поперечного ускорения на входе (или выходе) должен быть еще такой скачок в какой-то промежуточный момент, один или несколько. Но это уже другая постановка, с другой более сложной системой уравнений нежели система (18) и (21). Эта задача здесь не решалась. Педлагаем ее заинтересованному читателю.
Таблица 2
|
|
|
|
2.44193 | 0.16853 | 1.00000 | 0.06853 |
2.40000 | 0.17316 | 0.97984 | 0.06625 |
2.20000 | 0.19879 | 0.88186 | 0.05459 |
2.00000 | 0.23262 | 0.78104 | 0.04190 |
1.80000 | 0.28013 | 0.67794 | 0.02875 |
1.60000 | 0.35309 | 0.57354 | 0.01615 |
1.50000 | 0.40680 | 0.52131 | 0.01055 |
1.40000 | 0.48018 | 0.46939 | 0.00580 |
1.20000 | 0.74164 | 0.36765 | 0.00024 |
1.15528 | 0.83771 | 0.34550 | 0.00000 |
––––––––––––––––––––
Также, как и классическая фигура Инь-Ян, составленая из двух полу-окружностей, в целом линии типа Инь-Ян на рис. 1, 2, 6 не являются едиными аналитическими кривыми. Правая и левая части этих кривых сопряжены в центре, т.е имеют общую касательную, однако кривизна в этой точке меняет знак. Опытные наездники, по их описанию, ощущают проход через центр как приятный момент. Конь, как они это описывают, «меняет ногу» и на «мгновение невесомо повисает в воздухе в свободном падении». При этом наклон коня и всадника меняется на притивоположный.
5. Заключение
Полученные в данной работе траектории в равной степени применимы не только для лошади, но и для других активно движущихся объектов таких, как мотоцикл, велосипед, гоночный автомобиль и т.п.
Предлагаемый в данной работе подход и выведенные здесь уравнения применимы и при других граничных условиях. Траектория типа Инь-Ян не единственный способ поворта вращения в другую стороны. Можно, например, просто описать петлю. Соответствующую оптимальную траекторию можно найти из тех же уравнений при соответствующих граничных условиях. В самом общем случае эти уравнения позволяют оптимально решить любую смену характера движения. В связи с этим, нам представляется, что предлагаемый здесь подход может оказаться полезным в дорожном строительстве при проектировании, например, развязок дорог при их пересечении, т.н. розеток [10].
Полезно подчеркнуть, что предлагаемый здесь вариацонный подход коренным образом отличается от т.н. принципа наименьшего действия [11] в классической механике в виде лангранжева или гамильтонова формализмов [12]. Варьируемые аргументы здесь – скорости, а не обобщенные координаты, как в формализме Лагранжа. Поэтому здесь отсутствуют обычные механические понятия такие, как энергия, импульс и т.п. Предполагается однако, что активно движущийся объект обладает достаточной внутренней энергией для поддержания движения. При необходимости, конечно, можно произвести анализ расхода и диссипации этой энергии, но это выходит за рамки данной работы.
Данную работу следует отнести к области науки, пока, видимо, не имеющей названия и которую следует назвать активной механикой. К этой области можно отнести также работы, посвященые исследованию движения микроорганизмов, как например [13], а также механике ходьбы (бега) [14] и других способов передвижения живых существ. Наш феноменологический подход позволяет исследовать движение в целом отдельно от деталей его механизмов и физиологии усталости, трудно поддающиеся математической формализации.
Сюда также можно отнести работы по реактивному движению с переменной массой, в основе которых лежит известное уравнение Мещерского [15]и которые также предлагают задачи на оптимизацию, например, расчет наиболее эфективного расхода топлива при заданных граничных условиях..
Активная и, если так можно выразиться, пассивная механика отличаются принципами причинности. В пассивной механике следствие с необходимостью подчиняется причине и действительно неизбежно следут ей мгновенно или с опозданием. В активной же механике, как и в жизни, истиная причина лежит всегда впереди, как определенная цель и задача состоит в оптимальном ее достижении.
Ссылки
- Уход за лошадью. http://en.wikipedia.org/wiki/Horse_care (дата обращения: 15.12.2011).
- Инь и янь, Википедия - свободная энциклопедия, <http://en.wikipedia.org/wiki/Yin_and_yang>. (дата обращения: 15.12.2011)
- Иньянь (инь-янь), Интернет-энциклопедия по философии, http://www.iep.utm.edu/yinyang/ (дата обращения: 15.12.2011).
- Тайцзи, Википедия - свободная энциклопедия, <http://en.wikipedia.org/wiki/Taiji> (дата обращения: 15.12.2011).
- Вариационное исчисление, Википедия - свободная энциклопедия, <http://en.wikipedia.org/wiki/Calculus_of_variations> (дата обращения: 15.12.2011).
- Функциональныепроизводные. http://mathworld.wolfram.com/FunctionalDerivative.html (дата обращения: 15.12.2011).
- Теорема Нетера, Википедия - свободная энциклопедия, http://en.wikipedia.org/wiki/Noether's_theorem (дата обращения: 15.12.2011).
- Метод Ньютона, Википедия - свободная энциклопедия, <http://en.wikipedia.org/wiki/Newton's_method> (дата обращения: 15.12.2011).
- MathWorks – Company - Компания MathWorks, < http://www.mathworks.com/index.html> (дата обращения: 15.12.2011).
- TransportAdvicePortal: JunctionDesign – Транспортный консультационный портал: Разработка развязок, http://tap.iht.org/ (дата обращения: 15.12.2011).
- Принцип наименьшего действия, Википедия - свободная энциклопедия, <http://en.wikipedia.org/wiki/Principle_of_least_action> (дата обращения: 15.12.2011).
- Лагранжева и гамильтонова механика. http://www.mathpages.com/home/kmath523/kmath523.htm (дата обращения: 15.12.2011).
- Креншау и др., Анализ трехмерной траектории организмов..., Журнал экспериментальной биологии 203 (6): 961.
- Клэр Т. Фарлей и др., Биомеханикаходьбы и бега. http://www.scribd.com/doc/35787151/Bio-Mechanics-of-Walking-and-Running (дата обращения: 15.12.2011).
- Аркадий Космодемьянский, Механика тел переменной массы, Большая Советская Энциклопедия, 3-е изд., 1970-1979.
Публикации с ключевыми словами: математическая модель, утомляемость коня, уравнения движения
Публикации со словами: математическая модель, утомляемость коня, уравнения движения
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



