научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 519.6
МГТУ им. Н.Э. Баумана
Введение
Решение многих современных практических задач, связанных с идентификацией и диагностированием сложных систем, обеспечением безопасности, оптимальным проектированием, управлением и т.п., предполагает применение методов многокритериальной оптимизации [1–3]. При наличии нескольких критериев целью оптимизации является поиск множества недоминируемых решений [4], образующих Парето-оптимальный фронт. Ввиду большой размерности и сложной структуры пространства поиска для большинства задач векторной оптимизации точное решение получить не удается. Одним из эффективных методов численного решения многокритериальных задач является векторный вариант метода линеаризации [5]. Используя построение сглаживающих аппроксимаций, можно расширить этот подход на негладкий случай [6]. Существенно, что отдельные критерии могут представлять собой многоэкстремальные не всюду дифференцируемые функции. В общем случае поиск глобального решения для такой критериальной функции представляет собой самостоятельную сложную задачу. Этим обусловлена актуальность разработки гибридных алгоритмов решения задач векторной оптимизации с многоэкстремальными негладкими критериями.
Эффективность детерминированных алгоритмов решения задач глобальной оптимизации существенно ограничена размерностью пространства поиска. В свою очередь, реализация мощных современных стохастических алгоритмов требует значительных вычислительных затрат. В работе [7] представлен гибридный алгоритм NMPCA, объединяющий стохастический алгоритм PCA и симплекс-метод Нелдера-Мида. При этом общий поиск решения в пространстве переменных проводится стохастическим алгоритмом, а затем перспективная область сканируется с использованием симплекс-метода. Однако метод Нелдера-Мида не всегда обеспечивает сходимость к стационарной точке, что снижает в целом надежность алгоритма MNPCA. В связи с этим в работе [8] представлен новый гибридный алгоритм, построенный на основе алгоритма PCA в сочетании с детерминированным методом линеаризации при локальном поиске. Градиентная информация, используемая в гибридном алгоритме, позволяет получить локально оптимальное, а следовательно, и глобальное решение задачи (если оно существует) при меньших вычислительных затратах по сравнению с алгоритмом PCA. При локальном поиске для многомерных не всюду дифференцируемых критериальных функций вводятся сглаживающие аппроксимации. Вместе с тем, существует класс оптимизационных задач, в которых использование градиентной информации или затруднено, или требует значительных вычислительных затрат. Этим объясняется интерес к разработке алгоритмов, не использующих производные критериальных функций по переменным задачи оптимизации. Второй гибридный алгоритм построен на основе алгоритма Метрополиса в сочетании с детерминированным методом редукции исходной многомерной задачи к эквивалентной одномерной. Редукция размерности пространства проводится при локальном поиске с использованием метода построения кривой, заполняющей пространство [9], по схеме Пеано-Гильберта. Решение задач глобальной оптимизации для отдельных критериев позволяет определить множество недоминируемых решений многокритериальной задачи, аппроксимирующих искомый фронт Парето.
В первом разделе вводятся некоторые определения и формулируется задача многокритериальной оптимизации. Краткое описание гибридных алгоритмов приведено во втором разделе. Предложенный подход позволяет находить глобальные решения для отдельных критериев, не являющихся всюду дифференцируемыми. В третьем разделе приводятся сведения о реализации алгоритма в виде прикладной программы. Численный пример применения гибридного алгоритма рассматривается в четвертом разделе, где представлены результаты решения стандартной эталонной тестовой задачи векторной оптимизации, а также приведены оценки эффективности алгоритма.
1. Постановка задачи
Пусть заданы функции ![]()
![]() образующие векторный критерий
образующие векторный критерий ![]() некоторой многокритериальной задачи оптимизации при ограничениях
некоторой многокритериальной задачи оптимизации при ограничениях ![]() , где
, где ![]() вектор переменных управления;
вектор переменных управления; ![]() функции ограничений; множество индексов
функции ограничений; множество индексов ![]() . Будем рассматривать задачу векторной оптимизации в предположении, что частные критерии и функции ограничений являются непрерывными многоэкстремальными не всюду дифференцируемыми функциями. В соответствии с [4] введем определения.
. Будем рассматривать задачу векторной оптимизации в предположении, что частные критерии и функции ограничений являются непрерывными многоэкстремальными не всюду дифференцируемыми функциями. В соответствии с [4] введем определения.
Определение 1. Решение ![]() называется слабо эффективным (эффективным или Парето-оптимальным), если не существует такого
называется слабо эффективным (эффективным или Парето-оптимальным), если не существует такого ![]() , что
, что ![]() .
.
Определение 2. Решение ![]() называется собственно эффективным (оптимальным по Джоффриону), если оно эффективное и существует такое положительное число
называется собственно эффективным (оптимальным по Джоффриону), если оно эффективное и существует такое положительное число ![]() , что для любого
, что для любого ![]() и
и ![]() , для которых выполнено неравенство
, для которых выполнено неравенство ![]() , и некоторого
, и некоторого ![]() , такого, что
, такого, что ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
Определение 3 [3]. Парето-оптимальное множество ![]() данной многокритериальной задачи
данной многокритериальной задачи ![]() определяется в виде:
определяется в виде: ![]() .
.
Определение 4 [3]. Для данной многокритериальной задачи и Парето-оптимального множества ![]() фронт Парето определяется в виде
фронт Парето определяется в виде
![]() .
.
2. Алгоритмы решения задачи со сглаживающей аппроксимацией
Построим алгоритм решения рассматриваемой задачи, реализующий вариант метода линеаризации для задач многокритериальной оптимизации [5]. Для каждой функции, представляющей частный критерий или функцию ограничений, введем двухпараметрическую сглаживающую аппроксимацию, предложенную в работе [6].
Следуя работе [5], свяжем с каждой точкой ![]() вспомогательную задачу
вспомогательную задачу

 , (1)
, (1)
где ![]() вектор направления поиска;
вектор направления поиска; ![]() параметр;
параметр; ![]() градиент сглаживающей аппроксимации критериальной функции
градиент сглаживающей аппроксимации критериальной функции ![]() , вычисленный в допустимой точке
, вычисленный в допустимой точке ![]() ;
; ![]() ; множество
; множество ![]() определено выше. Введем следующие предположения: пусть
определено выше. Введем следующие предположения: пусть ![]() слабо эффективное решение и существует такое
слабо эффективное решение и существует такое ![]() , что
, что
а) множество ![]() для
для ![]() ограничено;
ограничено; ![]() ;
;
б) градиенты функций ![]() в
в ![]() удовлетворяют условию Липшица с константой
удовлетворяют условию Липшица с константой ![]() ;
;
в) существуют такие множители Лагранжа задачи (1) ![]() что
что  , причем задача (1) разрешима относительно
, причем задача (1) разрешима относительно ![]() для любого
для любого ![]() .
.
Решением двойственной к (1) задачи являются некоторые функции ![]() и
и ![]() ; вектор
; вектор ![]() может быть представлен так:
может быть представлен так:
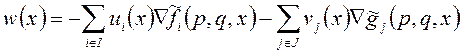 .
.
Далее при построении алгоритма используется ряд оценок изменений сглаживающих аппроксимаций функций ![]() и
и ![]()
![]() при сдвигах вдоль направлений, определяемых решением задачи (1).
при сдвигах вдоль направлений, определяемых решением задачи (1).
Алгоритм решения задачи векторной оптимизации включает в себя следующие основные шаги [5, 6]. Пусть ![]() начальное приближение и выбраны
начальное приближение и выбраны ![]() , и параметры аппроксимации
, и параметры аппроксимации ![]() . Пусть уже получена точка
. Пусть уже получена точка ![]() , тогда:
, тогда:
Шаг 1. Решить вспомогательную задачу (1) при ![]() .
.
Шаг 2. Найти первое значение ![]() при котором будет выполнено неравенство (4) для
при котором будет выполнено неравенство (4) для ![]() ; если такое
; если такое ![]() найдено, то положить
найдено, то положить ![]() ,
, ![]()
Если сглаживающие аппроксимации критериальных функций и функций ограничений построены, то, по теореме Да Канха-Полака-Джоффриона, необходимое условие слабой эффективности с учетом условия дополняющей нежесткости имеет вид:
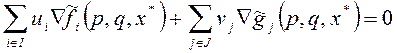 . (2)
. (2)
При некоторых предположениях о выпуклости рассматриваемых функций выражение (2) соответствует и достаточным условиям оптимальности точки ![]() . Если дополнительно предположить строгую выпуклость вектор-функции
. Если дополнительно предположить строгую выпуклость вектор-функции ![]() , то условия регулярности Коттла и равенства
, то условия регулярности Коттла и равенства ![]() будет необходимо и достаточно, чтобы точка
будет необходимо и достаточно, чтобы точка ![]() была эффективной (Парето-оптимальной). Следует отметить, что в любой предельной точке
была эффективной (Парето-оптимальной). Следует отметить, что в любой предельной точке ![]() , генерируемой данным алгоритмом, выполняются необходимые (а в выпуклом случае и достаточные) условия слабой эффективности (при дополнительном требовании на выполнение условия регулярности Коттла), собственной эффективности (при дополнительном требовании на выполнение условия обобщенной регулярности) и имеет место
, генерируемой данным алгоритмом, выполняются необходимые (а в выпуклом случае и достаточные) условия слабой эффективности (при дополнительном требовании на выполнение условия регулярности Коттла), собственной эффективности (при дополнительном требовании на выполнение условия обобщенной регулярности) и имеет место ![]() при
при ![]() .
.
3. Описание прикладных программ
Оптимизация частных критериальных функций проводится с использованием гибридного алгоритма глобальной оптимизации, объединяющего стохастический алгоритм PCA [7] и метод линеаризации при локальном поиске. Для не всюду дифференцируемых критериальных функций вводятся сглаживающие аппроксимации. Работа стохастического алгоритма PCA основана на использовании аналогии с физическими процессами абсорбции и рассеяния частиц при ядерных реакциях. В алгоритме PCA для исследования области поиска используется одна частица. На начальном шаге выбирается пробное решение (Old_Config), которое затем модифицируется посредством стохастического возмущения (Perturbation()), что позволяет найти новое решение (New_Config). С помощью функции Fitness() дается сравнительная оценка нового и предыдущего решений, на основании которой новое решение может быть принято или отвергнуто. Если новое решение отвергнуто, то происходит переход к функции Scattering(), реализующей схему Метрополиса. Новое решение принимается, если оно лучше предыдущего (абсорбция); если найденное решение хуже предыдущего, то происходит переход в отдаленную область пространства поиска (рассеяние), что позволяет преодолевать локальные минимумы. Второй алгоритм глобальной оптимизации построен на основе алгоритма Метрополиса в сочетании с детерминированным методом кривой, заполняющей пространство; последний применяется только при локальном поиске. Для решения задачи липшицевой минимизации исходная многомерная задача редуцируется к эквивалентной одномерной с использованием кривой Пеано, построение которой проводится по схеме Гильберта [10].
Версии гибридных алгоритмов многокритериальной оптимизации реализованы в виде прикладных программ. Программная реализация каждого алгоритма включает в себя: модули ввода исходной информации; модуль, реализующий основной цикл алгоритма, в том числе фазу случайных возмущений для перехода в новую область поглощения частицы, фазу исследования области поглощения, фазу возмущений в области рассеяния, фазу исследования решения в области рассеяния; модуль локального поиска методом редукции размерности; модуль вычисления текущего значения частного минимизируемого критерия; модуль формирования фронта Парето; модуль вывода результатов решения. Для определения параметров возмущения на соответствующих шагах гибридных алгоритмов используются стандартные встроенные генераторы случайных чисел. С целью получения оценки вычислительных затрат в программном обеспечении во всех случаях предусмотрены счетчики числа обращений к подпрограммам вычисления текущих значений критериальной функции. Проведено тестирование разработанного программного обеспечения и получены оценки вычислительной эффективности гибридных алгоритмов многокритериальной оптимизации.
4. Численный пример
Рассматривается стандартная эталонная тестовая задача ZDT4 [2]. Требуется решить бикритериальную задачу
найти ![]() , где
, где ![]() , при условиях:
, при условиях: ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Существенно, что функция ![]() , определяющая свойства критериальной функции
, определяющая свойства критериальной функции ![]() задачи, является многоэкстремальной. График функции
задачи, является многоэкстремальной. График функции ![]() в заданной области определения
в заданной области определения ![]() для
для ![]() представлен на рис. 1.
представлен на рис. 1.

Рис. 1.
Приближенное решение подзадачи глобальной минимизации частного критерия ![]() с использованием гибридного алгоритма PCASFC [10] иллюстрирует рис 2. Представлено изменение значений критериальной функции и переменной
с использованием гибридного алгоритма PCASFC [10] иллюстрирует рис 2. Представлено изменение значений критериальной функции и переменной ![]() при возрастании плотности развертки
при возрастании плотности развертки ![]() . Для определения множества недоминируемых решений задачи многокритериальной оптимизации требуется многократное решение подзадач глобальной минимизации при различных значениях переменной
. Для определения множества недоминируемых решений задачи многокритериальной оптимизации требуется многократное решение подзадач глобальной минимизации при различных значениях переменной ![]() и, соответственно, критериальной функции
и, соответственно, критериальной функции ![]() . На рис. 3 показан фронт Парето, представляющий решение задачи: сплошная линия соответствует точному решению; штриховая – приближенному решению, полученному с использованием программного обеспечения, реализующего гибридный алгоритм многокритериальной оптимизации (с редукцией размерности при глобальной минимизации частных критериев). Погрешность численного решения, аппроксимирующего фронт Парето, здесь не превышает 3.8 %.
. На рис. 3 показан фронт Парето, представляющий решение задачи: сплошная линия соответствует точному решению; штриховая – приближенному решению, полученному с использованием программного обеспечения, реализующего гибридный алгоритм многокритериальной оптимизации (с редукцией размерности при глобальной минимизации частных критериев). Погрешность численного решения, аппроксимирующего фронт Парето, здесь не превышает 3.8 %.
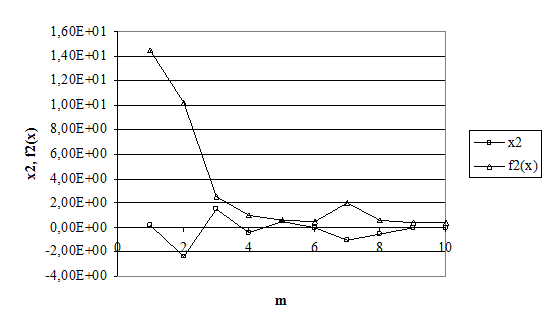
Рис. 2.

Рис. 3.
Следует отметить, что для решения одной подзадачи глобальной минимизации частного критерия ![]() потребовалось порядка
потребовалось порядка ![]() вычислений значений минимизируемой функции. Общее число обращений к подпрограммам вычисления значений критериальных функций определяется требованиями, предъявляемыми к точности построения аппроксимации фронта Парето.
вычислений значений минимизируемой функции. Общее число обращений к подпрограммам вычисления значений критериальных функций определяется требованиями, предъявляемыми к точности построения аппроксимации фронта Парето.
Заключение
Представлены новые гибридные алгоритмы решения задач векторной оптимизации с многоэкстремальными негладкими критериями. При определении глобальных оптимумов частных критериев используются гибридные методы, объединяющие алгоритм Метрополиса и детерминированные методы локального поиска. На основании анализа результатов, полученных с применением разработанного программного обеспечения для стандартного эталонного теста ZDT4 [2], можно сделать вывод о возможности получения решений задач рассматриваемого класса с достаточной точностью при приемлемом уровне вычислительных затрат.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (грант Президента РФ по поддержке научных исследований ведущих научных школ РФ, код НШ-4748.2012.8).
Литература
1. Gao J., Wang J. A hybrid quantum-inspired immune algorithm for multiobjective optimization // Applied Mathematics and Computat. – 2011. – V. 211, № 14. – P. 4754-4770.
2. Gil C., Márques A., Baños R., Montoya M.G., Gómez J. A hybrid method for solving multi-objective global optimization problems // Journal of Global Optimization. – 2007. – V. 38, № 2. – P. 265-281.
3. Zio E., Bazzo R. Multiobjective optimization of the inspection intervals of a nuclear safety system: a clustering-based framework for reducing the Pareto front // Annals of Nuclear Energy. – 2010. – Vol. 37, No. 5. – P. 798-812.
4. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. – 2-е изд., испр. и доп. – М.: ФИЗМАТЛИТ, 2007. – 256 с.
5. Пшеничный Б.Н., Сосновский Р.Б. Метод линеаризации для решения многокритериальной задачи оптимизации // Кибернетика. – 1987. – № 6. – С. 107-109.
6. Сулимов В.Д., Шкапов П.М. Сглаживающая аппроксимация в задачах векторной недифференцируемой оптимизации механических и гидромеханических систем // Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». – 2006, № 2. – С. 17-30.
7. Sacco W.F., Filho H.A., Henderson N., de Oliveira C.R.E. A Metropolis algorithm combined with Nelder-Mead Simplex applied to nuclear reactor core design // Annals of Nuclear Energy. – 2008. – Vol. 35, No. 5. – P. 861-867.
8. Сулимов В.Д. Локальная сглаживающая аппроксимация в гибридном алгоритме оптимизации гидромеханических систем // Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». – 2010, № 3. – С. 3-14.
9. Strongin R.G., Sergeev Y.D. Global optimization: Fractal approach and non-redundant parallelism // Journal of Global Optimization. – 2003. – V. 27, № 1. – P. 25-50.
10. Сулимов В.Д., Шкапов П.М. Глобальная минимизация липшицевой многомерной недифференцируемой функции с использованием гибридного алгоритма PCASFC. Свидетельство о государственной регистрации программы для ЭВМ № 2010613753. Зарегистрировано в Реестре программ для ЭВМ 9 июня 2010 г. – Федеральная служба по интеллектуальной собственности, патентам и товарным знакам, 2010.
Публикации с ключевыми словами: системы динамические, оптимизация многокритериальная, фронт Парето, алгоритмы гибридные
Публикации со словами: системы динамические, оптимизация многокритериальная, фронт Парето, алгоритмы гибридные
Смотри также:
- 77-30569/363023 Популяционные методы аппроксимации множества Парето в задаче многокритериальной оптимизации. Обзор.
- Оптимизация силовой части электрогидравлического следящего привода с дроссельным регулированием
- Постановка задачи управления фронтом Парето и ее решение в анализе и синтезе оптимальных систем
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



