научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2012
УДК 532.529.5
НИИ механики МГУ им. М.В. Ломоносова
МГТУ им. Н.Э. Баумана
Введение
Первые работы по исследованию поперечной миграции частиц в сдвиговых потоках были связаны с изучением движения крови в каналах. В 1836 году Пуазейль опубликовал работу, основанную на многочисленных экспериментах течения крови в каналах, в которой впервые было показано, что вблизи стенок каналов формируется область, свободная от частиц [1]. В последующих исследованиях обращено внимание на неоднородное распределение эритроцитов в течении крови в сосудах (например, [2, 3]). В [4] экспериментально исследовалось движение нейтрально плавучих частиц (плотность вещества частиц совпадает с плотностью несущей фазы) в течении Пуазейля в трубе при низких значениях чисел Рейнольдса основного течения. Было получено, что частицы в таком течении собираются в равновесном положении на расстоянии 0.6 радиуса трубы от оси симметрии. Этот эффект был назван авторами “Пинч” (“pinch”)-эффект ‒ частицы суспензии медленно мигрируют поперек основного потока и ниже по течению собираются в узкое кольцо, коаксиальное трубе. Далее последовала целая серия работ, в которых изучалось возникновение поперечной силы, действующей на сферу в сдвиговом потоке, в различных ситуациях. В [5] исследовалась поперечная миграция частиц в отсутствие их вращения, в [6-8] изучалось влияние отношения плотностей вещества частиц и несущей фазы, а также отношения радиуса частиц к радиусу трубы на положение частиц в вертикальном канале. В [9] рассмотрено влияние вращения на положение нейтрально плавучих частиц в каналах круглого и квадратного сечения. В перечисленных работах, помимо повторения эффекта, полученного Сегрэ и Зильбербергом [4], было получено, что радиус кольца частиц уменьшается, если скорость частиц меньше скорости основного потока и наоборот ‒ частицы собираются ближе к стенкам трубы, если их скорость выше скорости несущей фазы. В [10] исследовалась поперечная миграция частиц в течении суспензий в круглой трубе при различных значениях объемной доли частиц. Было показано, что область накопления частиц меняется в зависимости от объемной доли примеси и числа Рейнольдса, посчитанного по радиусу частиц и средней скорости потока. Частицы могут собираться в кольцо, на оси трубы, либо профиль концентрации может иметь два локальных максимума ‒ на оси симметрии и на некотором расстоянии от стенки. В [11] изучается трансформация кольца частиц, полученного в оригинальном опыте Сегрэ-Зильберберга, в зависимости от числа Рейнольдса основного течения. С увеличением числа Рейнольдса диаметр и ширина этого кольца увеличиваются. Эффект накопления частиц на определенном расстоянии от стенок канала предлагается использовать для фильтрации клеток, в проточной цитометрии (см., например, [12, 13]), при создании так называемой «лаборатории на чипе» ‒ миниатюрного устройства, позволяющего проводить один или несколько лабораторных процессов на одном чипе.
Первые теоретические исследования возникновения силы, поперечной основному потоку, относятся к 60-м годам прошлого века. В [14] было предложено выражение для поперечной силы, возникающей для закрученной сферы в однородном потоке (сила Магнуса). В [15] было показано, что при полном пренебрежении инерционными эффектами, поперечная сила, действующая на сферу в сдвиговом потоке, не возникает. Впервые выражение для подъемной силы, действующей на сферу в неоднородном потоке, было получено Сэфманом [16], который решил задачу об обтекании сферы плоскопараллельным сдвиговым потоком при малых, но конечных числах Рейнольдса. Было показано, что в сдвиговом потоке сила Сэфмана может заметно превосходить силу Магнуса. Ряд работ [16‒24] посвящен исследованию попереречной силы, действующей на сферу при конечных значениях чисел Рейнольдса обтекания частиц, и анализу влияния стенки на значение подъемной силы при малых числах Рейнольдса обтекания частиц. Впервые сила Сэфмана была включена в постановку задачи о течении запыленного газа в пограничном слое в работах [25, 26]. В сдвиговых потоках у стенки частицы могут оседать на начальном участке течения, а также накапливаться на определенном расстоянии от стенки [27, 28]. В [27] были получены предельные профили концентрации частиц. В [29] показана возможность формирования зон накопления частиц на границе пограничного слоя за ударной волной, движущейся с постоянной скоростью по запыленному газу или вдоль эродирующего слоя дисперсного осадка. В [30] теоретически и экспериментально продемонстрирован эффект фокусировки субмикронных аэрозольных частиц, движущихся в слабо сужающемся микрокапилляре диаметром порядка 10-4 м со скоростью порядка 100 м/с. В [31] исследуется поведение инерционных частиц за ударной волной, движущейся в узком канале постоянного сечения, и найден режим, соответствующий фокусировке частиц на оси канала.
В настоящей работе рассматриваются две модели течений дисперсных сред в пограничном слое на плоской пластине в поле силы тяжести. Исследуется поперечная миграция частиц, результаты численного моделирования сравниваются с известными экспериментальными данными [32, 33]. В [32] было экспериментально изучено распределение частиц в течении жидкости с примесью твердых частиц вдоль горизонтальной пластины. В [33] получены профили концентрации частиц в течении запыленного газа вдоль вертикально расположенной пластины. Обе экспериментальные работы показывают, что вблизи стенки концентрация частиц уменьшается. Во второй работе отношение плотностей несущей фазы и вещества частиц много меньше единицы. В таком случае движение частиц определяется силой аэродинамического сопротивления и силой Сэфмана, постановка задачи аналогична той, которая рассматривалась в [27]. В [32] рассматривается течение суспензии, в которой плотности жидкой и твердой фаз близки. Для этой задачи о течении суспензии в пограничном слое предложена модель, в которой в межфазном обмене импульсом также учитываются силы Архимеда, присоединенных масс и Бассэ-Буссинеска.
Постановка задачи
Рассматривается плоская задача о течении газа (жидкости) с примесью твердых частиц в пограничном слое на плоской стенке. Задача решается в рамках модели взаимопроникающих континуумов [34]. Несущая фаза – несжимаемая жидкость плотности ρ и вязкости μ. Дисперсные включения – одинаковые сферические частицы радиуса σ, массы m, ρsm – плотность вещества частиц; тензор напряжений в среде частиц отсутствует. Влиянием частиц на несущую фазу пренебрегается. В межфазном обмене импульсом учитываются сила аэродинамического сопротивления, подъемная сила, сила Архимеда, сила присоединенных масс и сила Бассэ-Буссинеска.
Вводится декартова система координат, ось x направлена вдоль стенки, начало координат находится на передней кромке пластины. Система уравнений для обеих фаз имеет вид (здесь и далее нижние индексы s относятся к параметрам дисперсной фазы, звездочкой обозначены размерные величины, которые в последующем следует отличать от аналогичных безразмерных величин):

Выражение для силы fs, действующей на одну частицу, имеет вид [35]:
![]()

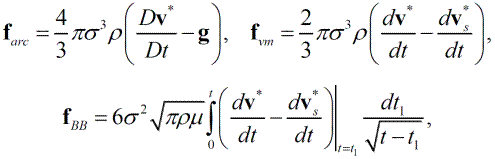

Здесь d/dt и D/Dt обозначают, соответственно, субстанциональные производные вдоль траекторий твердой частицы и частицы несущей фазы; g – ускорение свободного падения. fst, fsaf, farс, fvm, fBB – сила аэродинамического сопротивления, подъемная сила, сила Архимеда, сила присоединенных масс и сила Бассэ-Буссинеска. Выражения для силы аэродинамического сопротивления и подъемной силы взяты в формах, предложенных в работах [36, 37], учитывающих конечные значения чисел Рейнольдса обтекания частиц.
Параметры задачи приведем к безразмерному виду следующим образом (звездочкой обозначены размерные величины):

где L – характерная длина задачи, U0 – скорость набегающего потока.
Так как влиянием частиц на несущую фазу пренебрегается, поля параметров несущей фазы находятся из решения задачи Блазиуса для чистого газа. Параметры дисперсной фазы находятся с помощью лагранжева подхода [39]:
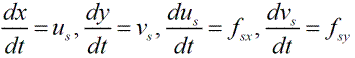
Здесь t – безразмерное время движения частицы вдоль траектории (масштаб при обезразмеривании времени L/U0), fsx, fsy – продольная и поперечная компоненты сил, действующих на единицу массы частицы. Начальные условия:
![]()
Полный лагранжев подход позволяет вычислять все параметры частиц, включая концентрацию, вдоль выбранных траекторий, что делает возможным исследовать течения с множественными пересечениями траекторий частиц и локальными зонами накопления дисперсной фазы. В случае течения суспензии, когда траектории частиц не пересекаются, концентрация определяется с помощью трубок тока дисперсной фазы. Взаимодействие частиц со стенкой не рассматривается.
Движение частиц определяется следующими безразмерными параметрами (выражение в скобках для случая, когда сила тяжести направлена вдоль стенки):

Параметр при подъемной силе выражается через основные следующим образом:

Выражения для текущих чисел Рейнольдса обтекания частиц таковы:
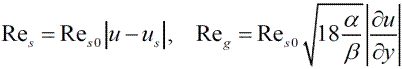
Течение суспензии в пограничном слое на горизонтальной пластине
В [32] рассматривается течение смеси «вода – твердые частицы» вдоль пластины длиной 244 см. Скорость набегающего потока – 40-50 см/с. Плотность вещества частиц – 1-2 г/см3, диаметр частиц – 100 мкм. Сечения, при которых проводились измерения: x1* = 2.5 см, x2* = 5 см, x3* = 7.5 см. В таблице приведены значения безразмерных определяющих параметров при U0 = 50 см/с, Res0 = 100, ω = 1,05•105.
α | β | ζ |
1 | 2200 | 1.2•106 |
0.91 | 2000 | 1.1•106 |
0.77 | 1700 | 1.2•106 |
В данной задаче различие между субстанциональными производными вдоль траекторий твердой частицы и частицы несущей фазы несущественно в силу того, что числа Рейнольдса обтекания частиц, посчитанные по относительной скорости, малы, и параметр инерционности β велик. Поэтому уравнения движения частиц можно упростить и переписать в виде:

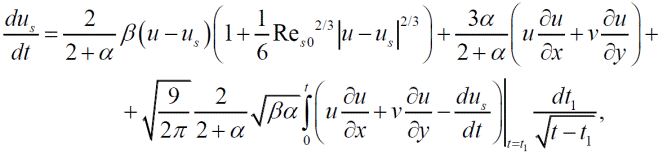
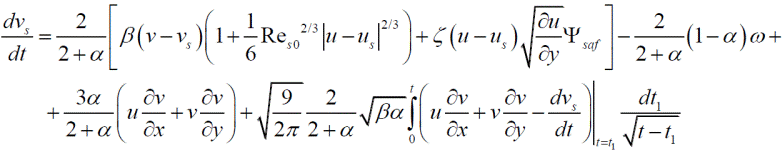
Концентрация частиц определяется из условия сохранения потока дисперсной фазы в трубке тока. Для двумерного случая, это условие принимает вид:
![]()
Данная система интегро-дифференциальных уравнений с начальными условиями (2) решалась численно. Несобственный интеграл разбивается на две части – с особенностью и без нее. В первой части интегрирование ведется от 0 до t ‒ ε, во второй – в ε-окрестности точки t. Данный алгоритм вычисления наследственной силы Бассе-Буссинеска был предложен и апробирован в работе [38]. Концентрация вычисляется с помощью трубок тока дисперсной фазы (4), с использованием интерполяции параметров частиц полиномами второго порядка.
Некоторые результаты расчетов приведены на рис. 1-4. В расчетах было положено: U0 = 50 см/с, Res0 = 100, ω = 1,05•105, α = 0.77, x1 = 0.01 (2.5 см), x2 = 0.02 (5 см), x3 = 0.03 (7.5 см), us0 = 1. На рис. 1 приведены траектории движения частиц. На рис. 2, 3 показано развитей профилей продольной и поперечной компонент скорости дисперсной фазы (пунктирной линией обозначены профили соответствующих компонент скорости несущей фазы) в зависимости от автомодельной переменной Блазиуса y/x1/2. В силу того, что частицы малоинерционны (параметр β принимает большие значения), продольная компонента скорости частиц в рассматриваемых сечениях принимает значения близкие к значениям продольной скорости несущей фазы. На начальном участке движение частиц определяется действием подъемной силы, частицы сначала движутся от стенки, далее они меняют направление движения и под действием силы тяжести осаждаются на стенку. На рис. 4 показаны рассчитанные профили концентрации дисперсной фазы, приведено сравнение результатов численного моделирования (сплошные линии) и эксперимента (точки). Как и в эксперименте, концентрация убывает в направлении стенки.

Рис. 1. Траектории частиц диаметра 100 мкм при Res0 = 100, ω = 1,05•105, α = 0.77.

Рис. 2. Профили продольной компоненты скорости частиц диаметра 100 мкм в сечениях x1, x2, x3, пунктирная линия – профиль продольной компоненты скорости несущей фазы.
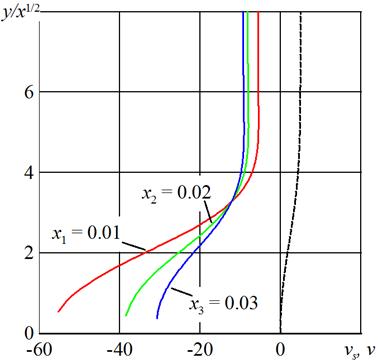
Рис. 3. Профили поперечной компоненты скорости частиц диаметра 100 мкм в сечениях x1, x2, x3, пунктирная линия – профиль поперечной компоненты скорости несущей фазы.
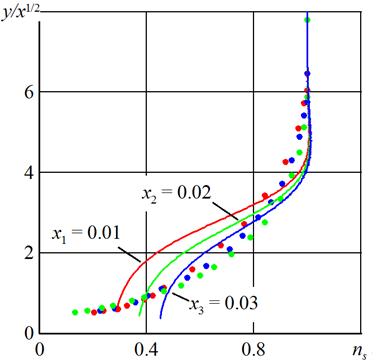
Рис. 4. Профили концентрации частиц диаметра 100 мкм в сечениях x1, x2, x3, точками обозначены результаты эксперимента [28] в тех же сечениях.
Течение запыленного газа в пограничном слое у вертикальной пластины
В [33] экспериментально исследовано течение запыленного газа вдоль вертикальной пластины. Несущая фаза – воздух, включения – твердые сферические частицы плотности 3.95 г/см3, радиус частиц 32 мкм, отклонение от данного размера частиц может достигать 30 %. Длина пластины – 50 см, скорость набегающего потока – 150 см/с. Сечения, в которых проводились измерения: x1* = 5 см, x2* = 10 см, x3* = 17 см. При таких параметрах эксперимента можно положить β = 1. Так как отношение плотностей воздуха и вещества частиц много меньше единицы, вместо α включим в набор определяющих параметров параметр при подъемной силе ζ. Безразмерные параметры принимают значения: Res0 = 3.36; ω = 0.0855, ζ = 3.88. Так как отношение плотностей газа и вещества частиц много меньше единицы, действием сил Архимеда, присоединенных масс и Бассэ-Буссинеска можно пренебречь (см. соответствующие коэффициенты в системе уравнений (3)). В таком случае уравнения движения части существенно упрощаются:

Концентрация частиц определяется с помощью полного лагранжева подхода [39], использующего лагранжеву форму уравнения неразрывности дисперсной фазы:
![]()

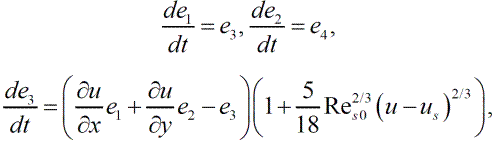

Первое уравнение – уравнение неразрывности в лагранжевых переменных, последние четыре – дополнительные уравнения для определения компонент якобиана, которые получаются дифференцированием системы уравнений (5) по параметру y0. Начальные условия для этой системы – условия (1), дополненные начальными значениями для дополнительных переменных:
![]()
Система обыкновенных дифференциальных уравнений (5)-(6) с начальными условиями (1), (7) решалась численно методом Рунге-Кутта четвертого порядка точности на выбранных траекториях частиц.
Некоторые результаты расчетов для профилей концентрации частиц приведены на рис. 5-8. В расчетах было положено Res0 = 3.36; ω = 0.0855, ζ = 3.88, us0 = 0.35; профили построены в сечениях, соответствующих экспериментам x1 = 2.55 (5 см), x2 = 5.1 (10 см), x3 = 8.7 (17 см). На рис. 5 приведены профили концентрации частиц, пунктирной линией показаны профили концентрации в тех же сечениях без учета действия боковой силы (здесь и далее для сравнения результатов численного моделирования и экспериментов концентрация частиц отнесена к ее значению вдали от стенки, приведены профили концентрации в зависимости от расстояния от стенки, отнесенного к толщине пограничного слоя). Под влиянием боковой силы, действующей на частицы в сдвиговом потоке, концентрация частиц при приближении к стенке убывает. Без учета подъемной силы поле концентрации частиц имеет особенность – неограниченно возрастает у стенки как и в [40]. На рис. 6 приведено сравнение результатов численного моделирования и экспериментальных данных. Получено качественное совпадение. При приближении к стенке концентрация частиц убывает, на некотором расстоянии от стенки профиль концентрации имеет локальный максимум. В численных расчетах локальный максимум профиля концентрации на некотором расстоянии от стенки исчезает ниже по потоку. Различие в результатах может быть объяснено тем, что в эксперименте использовались полидисперсные частицы. На рис. 7 приведено сравнение профилей концентрации частиц диаметра 32 мкм и частиц, размер которых на 30 % больше (соответствующие профили обозначены пунктирной линией). Для них значение максимума в каждом сечении больше.
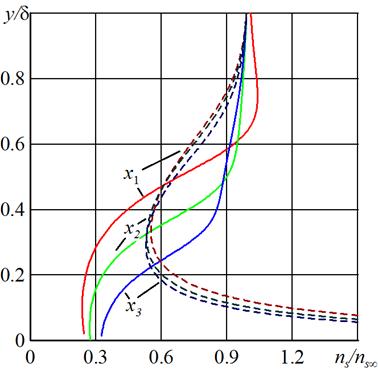
Рис. 5. Профили концентрации частиц диаметра 32 мкм в сечениях x1, x2, x3, пунктирная линия – профили концентрации частиц без учета поперечной силы.
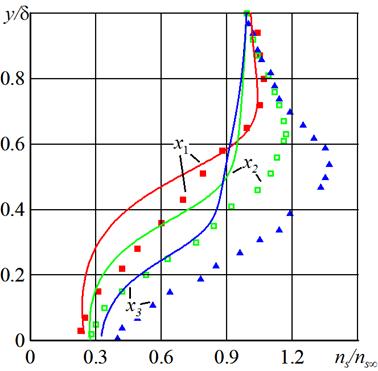
Рис. 6. Профили концентрации частиц 32 мкм в сечениях x1, x2, x3, точками обозначены результаты эксперимента [29] в тех же сечениях.

Рис. 7. Профили концентрации частиц диаметра 32 мкм в сечениях x1, x2, x3, пунктирные линии – профили концентрации частиц, диаметр которых на 30 % больше.
Заключение
В рамках модели двух взаимопроникающих континуумов решены задачи о течении газа (жидкости) с примесью твердых частиц в пограничном слое на плоской пластине в случае, когда массовая доля частиц пренебрежимо мала. В первой задаче рассматривается течение жидкости с примесью твердых частиц вдоль горизонтальной пластины, во второй – течение запыленного газа вдоль вертикальной пластины. В первом случае отношение плотностей несущей фазы и вещества частиц порядка единицы, поэтому помимо силы аэродинамического сопротивления и подъемной силы в межфазном обмене импульсом учитываются сила Архимеда, сила присоединенных масс и сила Бассе-Буссинеска. Во второй задаче о течении запыленного газа, когда плотность вещества частиц много больше плотности несущей фазы, поведение частиц определяется лишь силами аэродинамического сопротивления и Сэфмана.
Проведено параметрическое численное исследование профилей концентрации дисперсной фазы, формирующихся в пограничном слое. Получено качественное совпадение рассчитанных профилей концентрации частиц экспериментальным данным. Учет поперечной силы правильно описывает экспериментальные эффекты локальных максимумов концентрации частиц внутри пограничного слоя и уменьшения концентрации вблизи стенки. Некоторые количественные расхождения численных и экспериментальных результатов могут быть объяснены отсутствием полной информации о значениях параметров проведенных экспериментов (начальные рассогласования скоростей фаз, распределение частиц по размеру и проч.).
Работа поддержана РФФИ (№11-01-00483-а) и грантом президента РФ МК-3582.2011.1.
Список литературы:
- Poiseuille J.L.M. Recherches sur les causes du mouvement du sang dans les vaisseaux capillaires // Ann. Sci. Nat. 1836. Ser.2. T.5. P.111 ‒ 115.
- Taylor M. The flow of blood in narrow tubes. II. The axial stream and its formation, as determined by changes in optical density // Aust. J. Exp. Biol. Med. Sci. 1955. V. 33. Iss. 1. P.1 ‒ 16.
- Bayliss L. E. The axial drift of the red cells when blood flows in a narrow tube // J Physiol. 1959. Vol. 149. No 3. P.593 ‒ 613.
- Segre G., Silberberg A. Behaviour of macroscopic rigid spheres in Poiseuille flow. Pt. 2. Experimental results and interpretation // J. Fluid Mech. 1962. 14, 136 P. 136 ‒ 157.
- Oliver R. Influence of particle rotation on radial migration in the Poiseuille flow of suspensions // Nature. 1962. 194. P. 1269 ‒ 1271.
- Jeffrey R. C., Pearson J. R. A. Particle motion in laminar vertical tube flow // J. Fluid Mech. 1965. 22. P. 721 ‒ 735.
- Karnis A., Goldsmith H. L., Mason S. G. The flow of suspensions though tubes. V Inertial effects // Can. J. Chem. Engng. 1966. 44 P. 181 – 193.
- Aoki H., Kurosaki Y., Anzai H. Study on the tubular pinch effect in a pipe flow // Bull. JSME. 1979. 22. 164. P. 206 – 212.
- Tachibana M. On the behaviour of a sphere in the laminar tube flows // Rheol. Acta. 1973. 12. P. 58 – 69.
- Han M. [и др.] Particle migration in tube flow of suspensions // J. Rheol. 1999. 43. P. 1157 – 1174.
- Matas J.-P., Morris J.F., Guazzelli E. Inertial migration of rigid spherical particles in Poiseuille flow // J. Fluid Mech. 2004. 515. P. 171 ‒ 195.
- Bhagat A.A.S., Kuntaegowdanahalli S.S., Papautsky I. Enhanced particle filtration in straight microchannels using shear-modulated inertial migration // Phys. Fluids. 2008. V. 20. N 10. 101702.
- Kuntaegowdanahalli S.S, [и др.] Inertial microfluidics for continuous particle separation in spiral microchannels // Lab on a Chip. 2009. V. 20. Iss. 9. P. 2973 ‒ 2980.
- Rubinow S. I., Keller J. B. The transverse force on a spinning sphere moving in a viscous fluid // J. Fluid Mech. 1961. 11. P. 447 ‒ 459.
- Bretherton F. P. The motion of rigid particles in a shear flow at low Reynolds number // J. Fluid Mech. 1962. V. 14. Iss. 2. P. 284 ‒ 304.
- Saffman P.G. The lift on a small sphere in a slow shear flow. // J. Fluid Mech. 1965. V. 22. P. 385 ‒ 400. Corrigendum: // J. Fluid Mech. 1968. V. 31 P. 624.
- Dandy D.S., Dwyer H.A. Sphere in shear flow at finite Reynolds number: Effect of shear on particle lift, drag and heat transfer // J. Fluid Mech. 1990. V. 216. P. 381 ‒ 410.
- Асмолов Е.С. О динамике сферической частицы в ламинарном пограничном слое // Изв. АН СССР. МЖГ. 1990. N 6. C. 91 ‒ 96.
- McLaughlin J.B. Inertial migration of a small sphere in linear shear flows // J. Fluid Mech. 1991. V. 224. P. 261 ‒ 274.
- Асмолов Е.С. О движении дисперсной примеси в ламинарном пограничном слое на плоской пластине // Изв. АН СССР. МЖГ. 1992. N 1. C. 66 ‒ 73.
- McLaughlin J.B. The lift on a small sphere in wall-bounded linear shear flows // J. Fluid Mech. 1993. V. 246. P. 249 ‒ 265.
- Cherukat P., McLaughlin J.B. The inertial lift on a rigid sphere in a linear shear flow field near a flat wall // J. Fluid Mech. 1994. V. 263. P. 1 -- 18. Corrigendum: //J. Fluid Mech. 1995. V. 285. P. 407 ‒ 407.
- Asmolov E.S. The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number // J. Fluid Mech. 1999. V. 381. P. 63 ‒ 87.
- Asmolov E.S., Osiptsov A.A. The inertial lift on a spherical particle settling in a horizontal viscous flow through a vertical slot // Phys. Fluids. 2008. V. 20. N 12. 123301.
- Otterman B., Lee S.L. Particulate velocity and concentration profiles for laminar flow of a suspension over a flat plate // In: Proc. Heat Transfer and Fluid Mech. Inst Monterey, Calif: Stanford Univ. Press. 1970. P 311-322.
- Lee S.L., Chan W.K. Two-phase laminar boundary layer along a vertical flat wall // Hydrotransport. 1972. 1. N 2 (A-4,45-A4). P. 58.
- Осипцов А.Н. Движение запыленного газа в начальном участке плоского канала и круглой трубы // Изв. АН СССР. МЖГ. 1988. N 6. C. 80-87.
- Наумов В.А. Расчет ламинарного пограничного слоя на пластине с учетом подъемных сил, действующих на дисперсную примесь // Известия АН СССР. Механика жидкости и газа. – 1988. – № 6. С. 171-173.
- Ван Бо-И, Осипцов А.Н. Пристеночный пограничный слой за ударной волной в запыленном газе // Изв. РАН, МЖГ. 1999. № 4. С. 61 ‒ 73.
- AkhatovI.S. [и др.] Aerosol flow in microscale: Theory, experiment, and application to direct-write microfabrication // Proc. ECI Intern. Conf. Heat Transfer and Fluid Flow in Microscale. Whistler, Canada, 2008. P. 1.
- Осипцов А.Н., Рыбдылова О.Д. Фокусировка аэрозоля за ударной волной, движущейся в микроканале // Теор. основы хим. технологии. Т. 45, № 2, 2011, С. 178 ‒ 186.
- Lee S.L. Aspects of suspension shear flows // Adv. in Appl. Mech. 1982. V. 22. P. 1 ‒ 65.
- Hussainov M. [и др.] Properties of solid particle distribution in two-phase laminar boundary layers of various shapes and particle sedimentation // Proc. Estonian Acad. Sci. Phys. Math. 1994. V. 42. N. 4. P. 237 ‒ 249.
- Marble F.E. Dynamics of dusty gases // Ann. Rev. Fluid Mech. 1970. V. 2. P. 397 ‒ 445.
- Maxey M.R., Riley J.J. Equation of motion of a small rigid sphere in a nonuniform flow // Phis. of Fluids. 1983. V.26. P. 883-889.
- Carlson D.J., Hoglund R.F. Particle drag and heat transfer in rocket nozzles // AIAA Journal. 1964. V. 2. N 11. P. 1980 ‒ 1984.
- Mei R. An approximate expression for the shear lift force at finite Reynolds number // Intern. J. Multiphase Flow. 1992. V. 18. N 1. P. 145 ‒ 147.
- Невский Ю.А., Осипцов А.Н. О роли нестационарных и наследсвенных сил в задачах гравитационной конвекции // Вестн. Моск. Ун-та. Сер. 1. Мат., Мех. 2008. N 4 С. 37 ‒ 40.
- Осипцов А.Н. Развитие лагранжева подхода для моделирования течений дисперсных сред. В сб.: Проблемы современной механики. К 85-летию со дня рождения академика Г.Г. Черного. М.: Изд. МГУ, 2008. С. 390 ‒ 407.
- Осипцов А.Н. О структуре ламинарного пограничного слоя дисперсной смеси на плоской пластинке // Изв. АН СССР. МЖГ. 1980. N4. C. 48-54.
Публикации с ключевыми словами: пограничный слой, подъемная сила, частицы
Публикации со словами: пограничный слой, подъемная сила, частицы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



