научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 519.713; 510.5
МГТУ им. Н.Э. Баумана
В задачах вычислительной математики, криптографии, математического моделирования находят применение клеточные автоматы. Известен ряд связанных с клеточными автоматами задач, являющихся NP-полными. В настоящей статье доказывается NP-полнота еще одной задачи, связанной с клеточными автоматами – задачи о существовании предыдущего состояния обобщенного клеточного автомата. NP-полнота этой задачи важна как для теории клеточных автоматов, так и для прикладных наук, таких как криптография.
Классические клеточные автоматы впервые были предложены Дж. фон Нейманом в работе [9] и исследовались в работах [8, 10-13]. В работах [5, 6] исследовалась NP-полнота некоторых задач связанных с клеточными автоматами. Недавно, в работах [3, 4], было предложено и исследовано обобщение клеточных автоматов – неоднородные клеточные автоматы. Такие автоматы мы будем называть обобщенными.
Назовем обобщенным клеточным автоматом пару ![]() , где
, где ![]() – ориентированный мультиграф (V – множество вершин, а E – мультимножество ребер), с каждой вершиной которого ассоциирована булева переменная, причем все вершины пронумерованы числами
– ориентированный мультиграф (V – множество вершин, а E – мультимножество ребер), с каждой вершиной которого ассоциирована булева переменная, причем все вершины пронумерованы числами ![]() . Переменную, ассоциированную с i-ой вершиной, будем обозначать
. Переменную, ассоциированную с i-ой вершиной, будем обозначать ![]() . Такие переменные мы будем называть ячейками. Для каждой вершины входящие в нее ребра пронумерованы числами
. Такие переменные мы будем называть ячейками. Для каждой вершины входящие в нее ребра пронумерованы числами ![]() . Функция
. Функция ![]() – локальная функция связи.
– локальная функция связи.
Опишем теперь работу обобщенного клеточного автомата. В начальный момент времени каждая ячейка памяти ![]() ,
, ![]() имеет некоторое начальное значение
имеет некоторое начальное значение ![]() . Далее автомат работает по шагам. На шаге с номером tс помощью локальной функции связи вычисляются новые значения ячеек:
. Далее автомат работает по шагам. На шаге с номером tс помощью локальной функции связи вычисляются новые значения ячеек:
![]() ,
,
где ![]() – номер вершины, из которой исходит ребро, входящее в вершину i и имеющее номер j. Заполнение клеточного автомата на шаге tбудем обозначать
– номер вершины, из которой исходит ребро, входящее в вершину i и имеющее номер j. Заполнение клеточного автомата на шаге tбудем обозначать ![]() .
.
Пусть дан обобщенный клеточный автомат ![]() и его заполнение после первого шага
и его заполнение после первого шага ![]() . Задачу нахождения такого начального заполнения клеточного автомата
. Задачу нахождения такого начального заполнения клеточного автомата ![]() , которое после первого шага перейдет в заполнение
, которое после первого шага перейдет в заполнение ![]() , назовем задачей о восстановлении предыдущего состояния обобщенного клеточного автомата.
, назовем задачей о восстановлении предыдущего состояния обобщенного клеточного автомата.
Сформулируем теперь эту задачу в форме распознавания. Назовем задачей о существовании предыдущего состояния обобщенного клеточного автомата следующую задачу. Дан обобщенный клеточный автомат ![]() и его заполнение после первого шага:
и его заполнение после первого шага: ![]() . Распознать, существует ли начальное заполнение клеточного автомата
. Распознать, существует ли начальное заполнение клеточного автомата ![]() , которое после первого шага перейдет в заполнение
, которое после первого шага перейдет в заполнение ![]() .
.
Теперь докажем следующую теорему, являющуюся основным результатом этой работы.
Теорема 1. Задача о существовании предыдущего состояния обобщенного клеточного автомата является NP-полной.
Доказательство.
Задача о существовании предыдущего состояния принадлежит классу NP, поскольку в качестве сертификата можно рассматривать начальное заполнение.
Сведем задачу о 3-выполнимости (3-SAT), NP-полнота которой известна, к задаче о существовании предыдущего состояния.
Пусть дана 3-КНФ вида:
Задача о 3-выполнимости состоит в том, чтобы определить, существует ли такой набор аргументов ![]() , для которого
, для которого ![]() .
.
Сведем эту задачу к задаче о существовании предыдущего состояния обобщенного клеточного автомата. Для этого построим обобщенный клеточный автомат, граф которого состоит из ![]() вершин. В качестве локальной функции связи клеточного автомата, выберем функцию
вершин. В качестве локальной функции связи клеточного автомата, выберем функцию
![]() .
.
Теперь определим ребра графа (всего их ![]() ). Ориентированное ребро, исходящее из вершины aи входящее в вершину b, будем обозначать
). Ориентированное ребро, исходящее из вершины aи входящее в вершину b, будем обозначать ![]() . Рассмотрим j-ую дизъюнкцию, входящую в :
. Рассмотрим j-ую дизъюнкцию, входящую в : ![]() . Для каждой такой дизъюнкции добавим в граф четыре ребра.
. Для каждой такой дизъюнкции добавим в граф четыре ребра.
· Для каждого литерала ![]() из трех, входящих в рассматриваемую дизъюнкцию, добавим в граф ребро
из трех, входящих в рассматриваемую дизъюнкцию, добавим в граф ребро ![]() в случае, если
в случае, если ![]() и
и ![]() – в противном случае. Поставим в соответствие каждому такому ребру номер t.
– в противном случае. Поставим в соответствие каждому такому ребру номер t.
· Четвертым будет ребро ![]() с номером 4. Мы будем полагать, что
с номером 4. Мы будем полагать, что ![]() .
.
Проделав это для всех ![]() , получим, что если в первых nячейках разместить значения переменных, а в последующих nячейках разместить значения отрицаний переменных, клеточный автомат за один шаг вычислит значения всех q дизъюнкций из 3-КНФ .
, получим, что если в первых nячейках разместить значения переменных, а в последующих nячейках разместить значения отрицаний переменных, клеточный автомат за один шаг вычислит значения всех q дизъюнкций из 3-КНФ .
Теперь для каждого ![]() добавим три одинаковых ребра
добавим три одинаковых ребра ![]() с номерами 1,2,3 и ребро
с номерами 1,2,3 и ребро ![]() с номером 4. Эти ребра необходимы для того, чтобы гарантировать то, что
с номером 4. Эти ребра необходимы для того, чтобы гарантировать то, что ![]() .
.
Кроме того, добавим ребро ![]() , с номером 1; два одинаковых ребра
, с номером 1; два одинаковых ребра ![]() , с номерами 2 и 3 и петлю
, с номерами 2 и 3 и петлю ![]() , с номером 4. В результате такой конфигурации ребер, в вершине
, с номером 4. В результате такой конфигурации ребер, в вершине ![]() будет вычисляться:
будет вычисляться:

Теперь, если выполняется условие ![]() , для каждого
, для каждого ![]() добавим по четыре одинаковых петли
добавим по четыре одинаковых петли ![]() .
.
Положим теперь:
· ![]() для
для ![]() ;
;
· ![]()
· если выполняется условие ![]() , то
, то ![]() для
для ![]() .
.
Легко видеть, что такое заполнение может получиться в том и только в том случае, если выполняются следующие условия:
· ![]() ;
;
· ![]() для всех
для всех ![]() ;
;
· ![]()
· Начальное значение остальных ячеек произвольно.
Другими словами, если начальное заполнение существует, то существует и набор, на котором выполняется 3-КНФ .
Таким образом, задача о 3-выполнимости сводится к задаче о существовании предыдущего состояния обобщенного клеточного автомата. Из этого следует NP-полнота этой задачи. Теорема доказана. □
Итак, задача о существовании предыдущего состояния обобщенного клеточного автомата является NP-полной, а задача восстановления этого состояния, распознавательным аналогом которой является задача о существовании предыдущего состояния, является NP-трудной. NP-трудность этой задачи сохраняется, если рассматривать все обобщенные клеточные автоматы, отличные от классических. В то же время, в случае двухместности локальной функции связи f, задача о существовании предыдущего состояния принадлежит классу P. Докажем этот факт в следующей теореме.
Теорема 2. Задача о существовании предыдущего состояния обобщенного клеточного автомата, локальная функция связи которого зависит от двух переменных, принадлежит классу P.
Доказательство.
Если локальная функция связи fзависит от двух переменных, то задача о существовании предыдущего состояния состоит в том, чтобы определить, существует ли решение системы булевых уравнений:
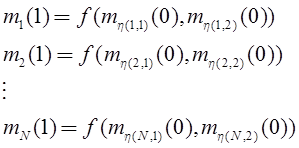 ,
,
относительно начального заполнения. Правые части этих уравнений легко представляются в виде 2-КНФ.
Эта система уравнений эквивалентна уравнению:
 .
.
Легко видеть, что задача о наличии решений этого уравнения представляет собой принадлежащую классу P задачу о 2-выполнимости [7]. □
Доказанные в статье теоремы важны для обоснования криптостойкости систем шифрования, основанных на обобщенных клеточных автоматах [1-4].
Литература
1. Ключарев П.Г. Клеточные автоматы, основанные на графах Рамануджана, в задачах генерации псевдослучайных последовательностей // Наука и образование. Электронное научно-техническое издание. – 2011. – №10. – http://technomag.edu.ru/doc/241308.html.
2. Ключарев П.Г. Криптографические свойства клеточных автоматов, основанных на графах Любоцкого-Филипса-Сарнака // Безопасные информационные технологии. – М.: НИИ радиоэлектроники и лазерной техники. – 2011. – C. 163-173.
3. Сухинин Б.М. Исследование характеристик лавинного эффекта в двоичных клеточных автоматах с равновесными функциями переходов // Наука и образование: электронное научно-техническое издание. – 2010. – №8. – http://technomag.edu.ru/doc/159565.html.
4. Сухинин Б.М. Разработка генераторов псевдослучайных двоичных последовательностей на основе клеточных автоматов // Наука и образование: электронное научно-техническое издание. – 2010. – №9. – http://technomag.edu.ru/doc/159714.html.
5. Durand B. A random NP-complete problem for inversion of 2D cellular automata // Theoretical computer science. – 1995. – Vol. 148, №1. – 19-32.
6. Green F. NP-complete problems in cellular automata // Complex Systems. – 1987. – Vol. 1, №3. – 453-474.
7. Krom M.R. The Decision Problem for a Class of First Order Formulas in Which all Disjunctions are Binary // Mathematical Logic Quarterly. – 1967. – Vol. 13, №1. – 15-20.
8. Packard N.H., Wolfram S. Two-dimensional cellular automata // Journal of Statistical Physics. – 1985. – Vol. 38, №5. – P.901-946.
9. von Neumann J. The general and logical theory of automata // Cerebral mechanisms in behavior. – 1951. – P. 1–41.
10. Wolfram S. Cryptography with cellular automata // CRYPTO'85 Proceedings. – 1986. – P. 429-432.
11. Wolfram S. Statistical mechanics of cellular automata // Reviews of Modern Physics. – 1983. – Vol. 55, №3. – 601 p.
12. Wolfram S. Theory and applications of cellular automata // Advanced Series on Complex Systems, Singapore: World Scientific Publication, 1986. – 1986. – Vol. 1.
13. Wolfram S. Universality and complexity in cellular automata // Physica D: Nonlinear Phenomena. – 1984. – Vol. 10, №1-2. – P. 1-35.
Публикации с ключевыми словами: клеточный автомат, NP-полнота
Публикации со словами: клеточный автомат, NP-полнота
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




