научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 539.4
МГТУ им. Н.Э. Баумана
Актуальность вопроса катастрофических разрушений конструкций, к сожалению, не только не снижается в наше время, а, наоборот, возрастает. Проводимые расследования зачастую указывают на ошибки при проектировании: неполный учет действующих нагрузок, что приводит к возникновению колебаний и резонансу. При этом развивается большое число разориентированных трещин, что и приводит к катастрофе. Как отмечено в [2], анализ известной катастрофы Такомского моста «указал на необходимость динамического расчета мостов» и экспериментальных исследований параметров их колебаний (собственных частот и угловых подвижек) [5].
Анализ работ ученых [1-5], работающих в области теории упругости и механики разрушения, свидетельствует о том, что теоретический анализ в этих областях – это очень сложная и трудоемкая задача.
Разрушение – это предмет изучения теории прочности, теории разрушения или механики разрушения и сопротивления материалов. Однако ввиду актуальности проблемы безопасности и целостности как строительных сооружений, так и любых других конструкций и приборов, этими вопросами занимаются ученые различных областей науки и техники. Подходы, терминологии и приемы решения задач, связанные с определением сопротивления разрушению очень разнообразны и специфичны для каждой области науки, что может приводить к непониманию между специалистами смежных областей, решающих одни и те же задачи. Обычно специалисты в области теории разрушения анализируют изменение напряжений в теле исследуемого объекта при возникновении трещины. Чаще всего аналитические исследования проводятся с помощью МКЭ и компьютерного пакета ANSIS. При появлении трещины изменяются напряжения и смещаются узлы сетки, с помощью которой объект был разбит на конечные элементы. Одним из интересных экспериментальных способов является способ смещения муаровых полос, основанный на явлении механической интерференции при освещении поверхности объекта пучком света. Но такие методы пригодны для небольших объектов, которые можно исследовать в условиях лаборатории.
Настоящая работа посвящена вопросу выявления признаков, по которым можно было бы определить место расположения опасного сечения. Известно [4], что при появлении трещин в конструкции начинает падать основная (первая) собственная частота.
Для анализа выбираем частотную математическую модель – модель колебаний системы с распределенными параметрами. Представим пролет моста (рис. 1) в виде прямолинейного стержня или балки, шарнирно опертой на концах (рис. 2), и рассмотрим ее уравнение изгибных колебаний.

Рис. 1. Ворошиловский мост в Ростове-на-Дону
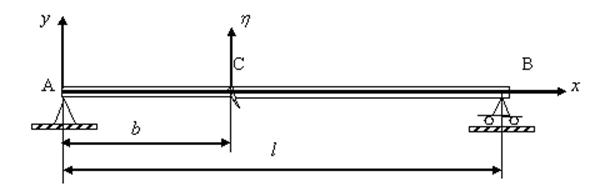
Рис.2. Модель шарнирно опертой балки
Математическая модель для целостной шарнирно опертой балки известна [6]. Рассмотрим эту модель.
Частотные методы исследования предполагают решение волнового уравнения. Дифференциальное уравнение изгиба балки – это волновое уравнение в частных производных (1) относительно амплитуд (при условии, что диаметр и свойства поперечного сечения стержня постоянны):

![]()
![]()
![]()
Решение уравнения (1) можно представить в виде (2) или (3), где Aj(x) – функция только абсциссы, представляющая собой амплитудное смещение (искомая форма собственных колебаний для j– той частоты).


Если подставить (3) в (1), то получается обыкновенное дифференциальное уравнение (4) относительно амплитуды Aj(x) для ![]() той частоты:
той частоты:
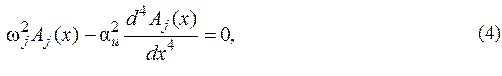
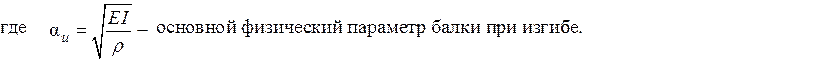
Для решения (4) необходимо задать граничные и начальные условия для левого и правого концов балки:
![]()
![]()
Для шарнирного стержня равны нулю вертикальные смещения и изгибающие моменты на концах. Равенство нулю изгибающего момента математически сводится к равенству нулю второй производной от смещения по х.
Начальные условия, т.е. начальное распределение, задается смещением и скоростью всех точек стержня в момент времени t=0.
Уравнения решаются с помощью преобразований Лапласа и функций А.Н. Крылова – S,T,U,V, которые связаны между собой условиями (6):
![]()
![]()
Окончательно решение принимает вид (7) или (8).
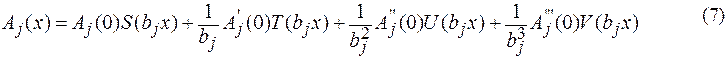
![]()
из граничных условий.
Из условий на левом конце вытекает, что C1=C3=0. Тогда выражение для амплитуд примет вид (9).
![]()
Используя условия на правом конце получим систему уравнений (10) относительно A’j(0) иA’’’j(0) или систему (11) относительно C1 и С2.
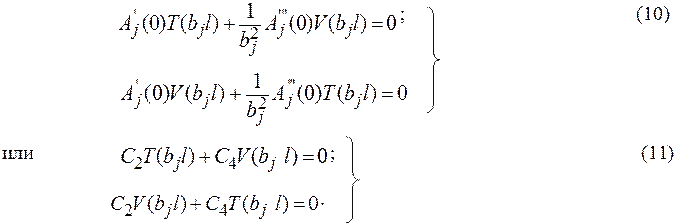
Система может иметь отличные от нуля решения только в том случае, если ее определитель равен нулю, т.е. (12) или (13) и (14),
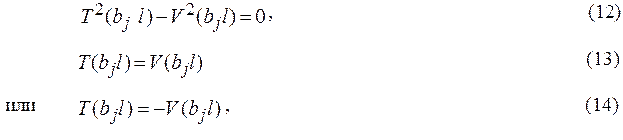
что возможно только при условиях (15):
![]()
которые удовлетворяются решением (16):
![]()
Таким образом, для балки на шарнирных опорах частоты определяются по формулам (17), т.е. собственные частоты пропорциональны квадратам натуральных чисел:
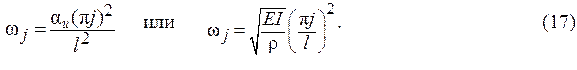
Уравнение упругой линии можно переписать в виде (18).
 (18)
(18)
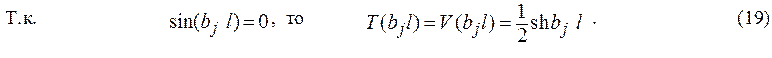
С учетом (19) запишем (10) в виде (20):

Откуда
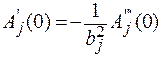 .
.
Формы собственных колебаний (упругой линии) имеют вид (21):
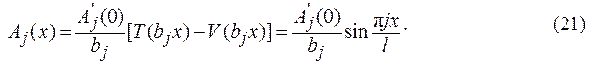
где Aj(0) – величина произвольная, которая зависит от Н.У.
Поэтому собственное колебание можно записать и так:
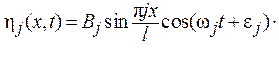
Ниже приведены формы пяти собственных колебаний для n=1,2,3,4,5.
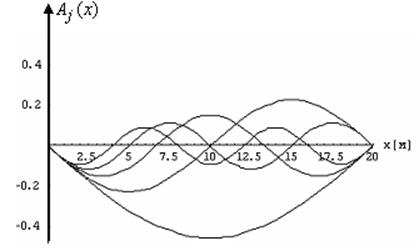
Рис. 3. Формы собственных колебаний
Для выявления критерия локализации проблемного сечения необходимо построить модель, учитывающую положение трещины по длине пролета. Присоединение дополнительной точечной массы на стержне приводит к такому же снижению основной собственной частоты, как и появлении трещины. Поэтому используем известную [6] модель – модель балки с точечным грузом. Расчетная схема показана на рис.4.
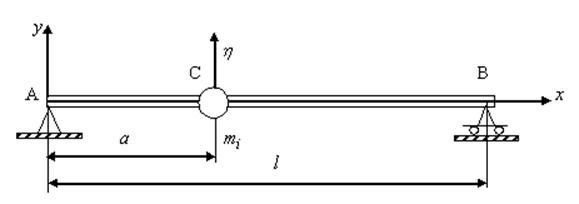
Рис.4. Модель балки с точечным грузом
В случае сосредоточенной массы в этой точке прикладывается сила инерции (22).

где Aj –величина амплитуды в точке присоединения массы mi.
Амплитудное значение силы обозначено:
![]()
Сопряжение участков выполняется следующим образом.
В случае общего для обоих участков начала отсчета принимается, что поперечные силы для правого и левого участков отличаются на величину ![]() :
:
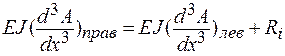
Выражение функции Aiдля правого и левого участка отличаются дополнительным слагаемым (см.23), где a – расстояние от начала координат до присоединенного груза.
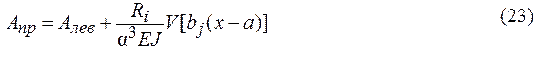
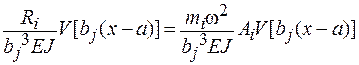
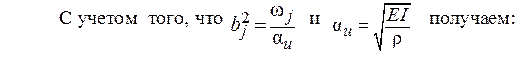
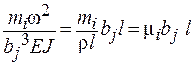
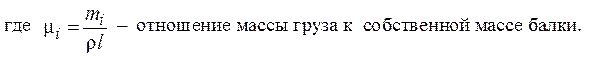
![]()
![]()
Прогиб для правого участка (x>a) можно представить в виде (24), где C2и С4 – некоторые постоянные.
![]()
Если использовать граничные условия для конца балки (25):

то можно получить уравнения (26) относительно этих постоянных:
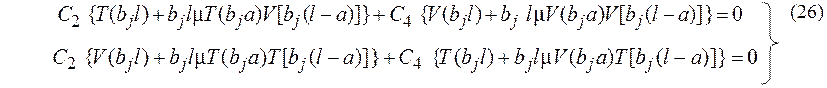
Уравнения будут иметь отличные от нуля решения, если определитель системы (26) будет равен нулю.
Таким образом, получается уравнение частот (27), которое нам необходимо для анализа:

Проанализируем это уравнение для различных значений масс и местоположений присоединенного груза. На рис.5 показано изменение частот при увеличении массы (при 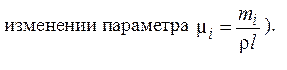
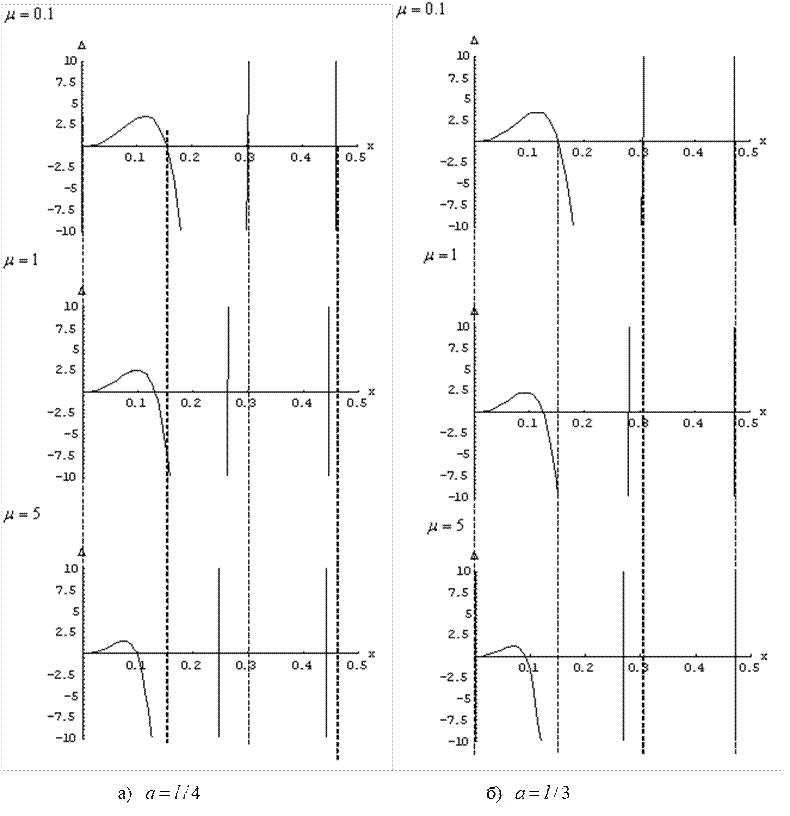
Рис.5. Сдвиг частот при изменении массы 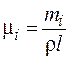 в точках
в точках ![]() и
и ![]()
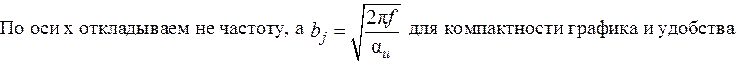 анализа. По оси у отложено значение определителя (37). Точки пересечения графика с осью х являются решением уравнения (37).
анализа. По оси у отложено значение определителя (37). Точки пересечения графика с осью х являются решением уравнения (37).
На рис. 5 – рис. 6 показан сдвиг частот при изменении массы (груз находится в точках ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно).
соответственно).
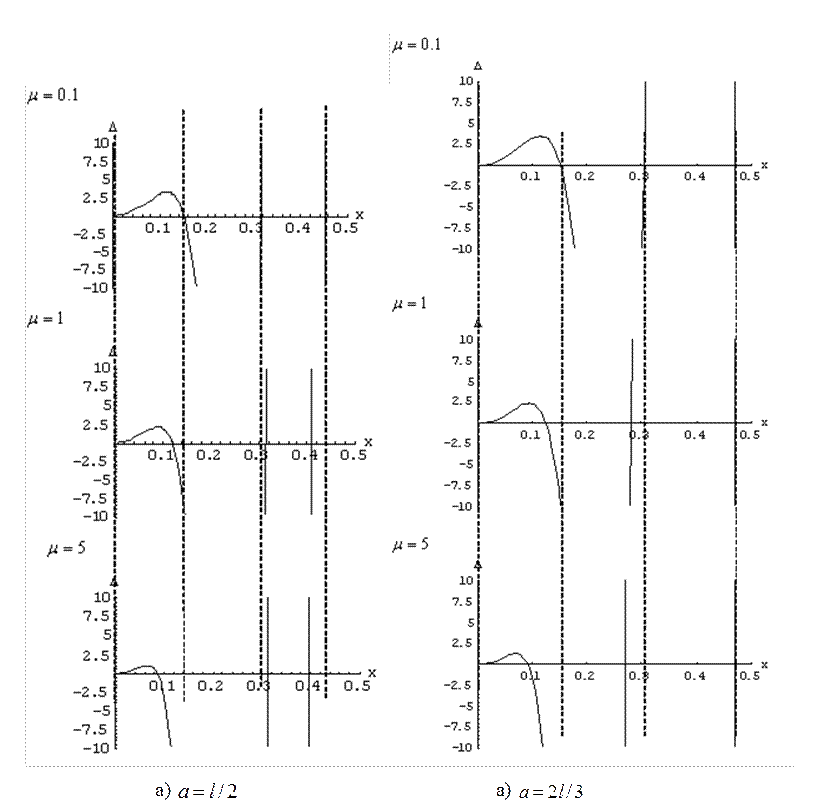
Рис. 6. Сдвиг частот при изменении массы 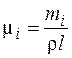 (груз в точке
(груз в точке ![]() и
и ![]() )
)
На рис. 7 и рис. 8. показан сдвиг частот при перемещении массы вдоль стержня
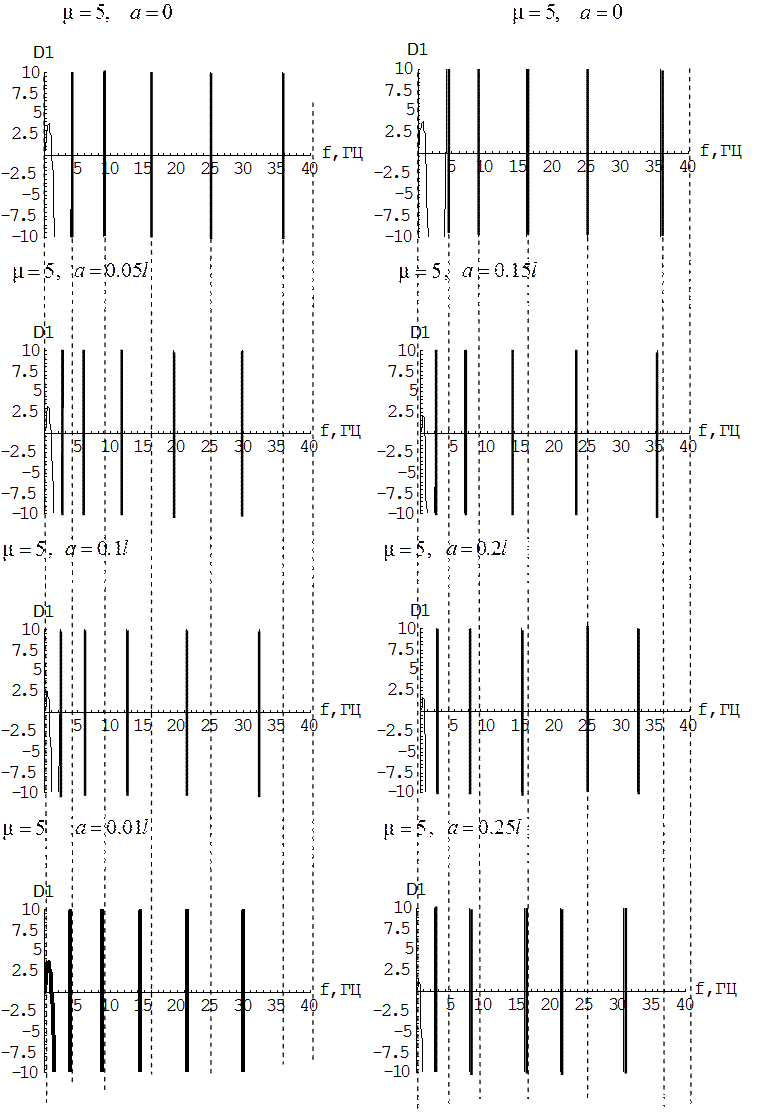
Рис. 7. Сдвиг частот при перемещении массы вдоль стержня вблизи опоры (![]() ).
).
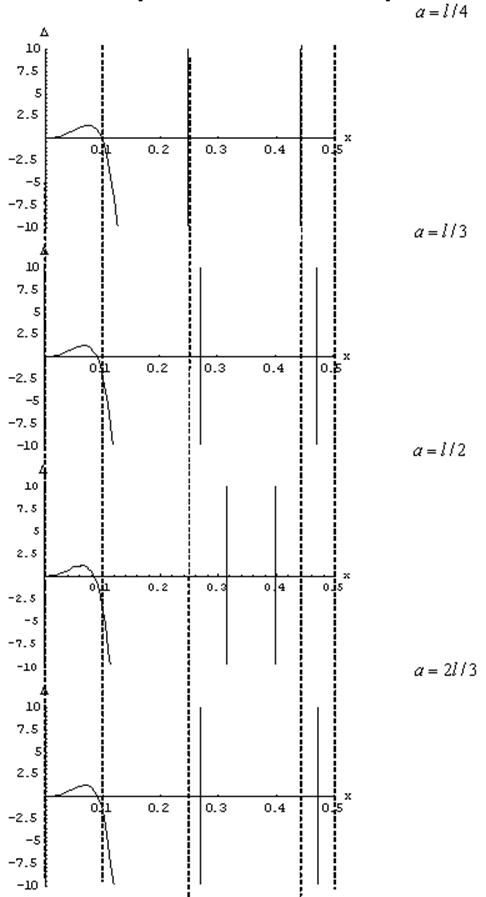
Рис.8. Сдвиг частот при перемещении массы вдоль стержня (![]() ).
).
Проанализируем полученные результаты. Во всех случаях характер изменения частот одинаков. Это видно на рис. 8 и рис.9, где по оси абсцисс отложено положение груза на балке в относительных единицах (![]() ), а по оси ординат – изменение частоты в Гц для каждого положения груза на балке.
), а по оси ординат – изменение частоты в Гц для каждого положения груза на балке.
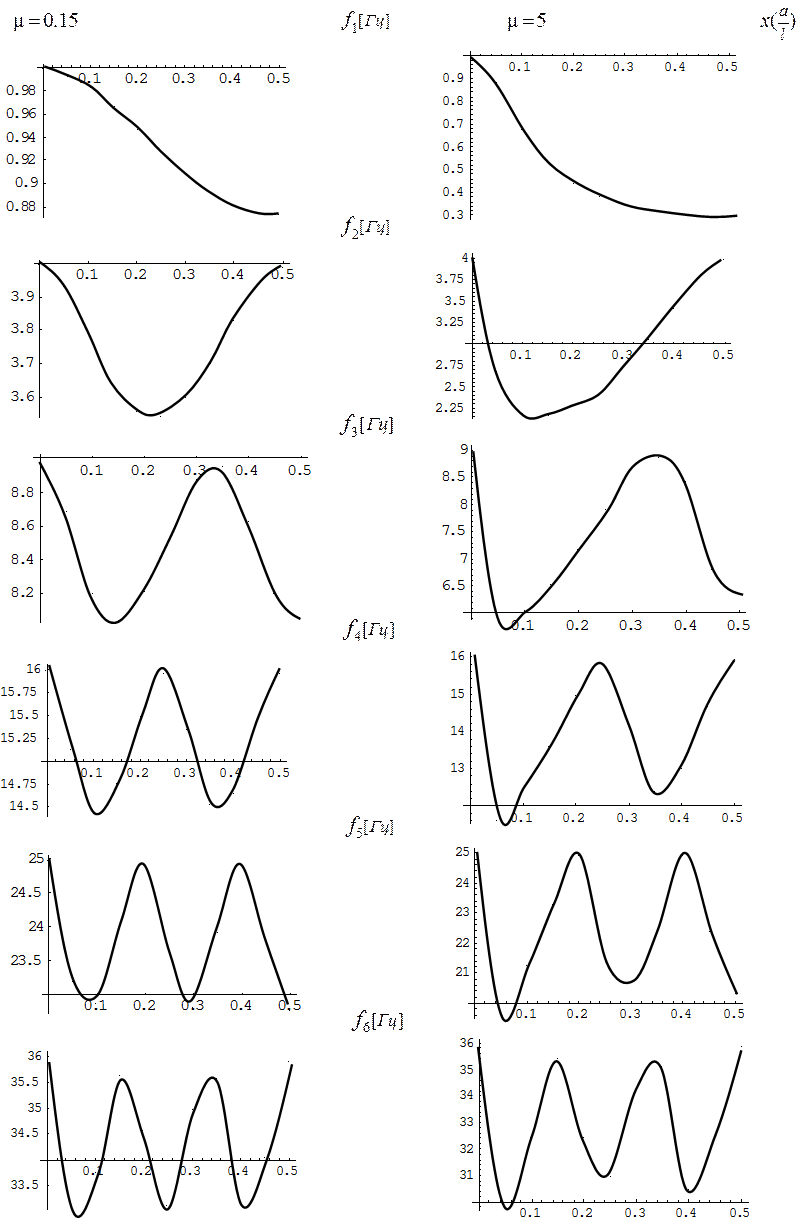
Рис. 8. Изменение частот в зависимости от положения груза относительно балки
На рис. 9 для наглядности совмещены все 6 графиков.

Рис.9. Совмещенные графики частот
Анализируя величину падения частот, можно выявить некоторые закономерности:
- Если появилось опасное сечение, то основная частота падает.
- Если для 2-ой, 4-ой и 6-ой частот одновременно наблюдается малое падение, а для 5-й и 3-ей одновременно – большое, то опасное сечение в середине балки.
- Если мало падение 3-ей частоты и велико 4-ой одновременно, то опасное сечение находится на расстоянии 1/3 от одной из опор.
- Если мало падение 4-ой и велико падение 6-ой частот одновременно, то опасное сечение находится на расстоянии 1/4 от одной из опор.
- Если велико падение всех частот одновременно, то опасное сечение находится вблизи опор (a=0.05l).
- Малое падение 6-ой частоты наблюдается в точках балки a=0.15l , a=0.35l , a=0.5l.
Т.е. совокупность величин падения частот на различных гармониках можно принять за некоторый признак места расположения опасного сечения.
Литература
1. Басс В.Н., Ивановский Е.А., Коновалов С.Ф. Система для мониторинга строительных сооружений // Доклад на научно-практической конференции «Современные системы и средства комплексной безопасности и противопожарной защиты объектов строительства».- АСУ «Дом на Брестской» , 2007.
- Партон В.З. Механика разрушения: От теории к практике. Изд. 2-е. М.: Издательство ЛКИ, 2007. 240 с.
- Партон В.З., Морозов Е.М. Механика упругопластического разрушения: Основы механики разрушения: Учебное пособие / Предисл. Ю.Н. Работнова. Изд.3-е, испр. М.: Издательство ЛКИ, 2008. 352 с.
- Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем: Современные концепции, парадоксы и ошибки. Изд. 6-ое, стереотипное. М.: КомКнига,2007. 352 с.
- Прецизионные системы мониторинга / С.Ф. Коновалов, Е.А. Ивановский, Е.Л. Межерицкий и др.// Высотные здания. – 2008. – Апрель/май. С. 120-125.
- Расчеты на прочность в машиностроении / С.Д. Пономарев, В.Л. Бидерман, К.К.Лихарев и др.; Под ред. С.Д. Пономарева. М.: Машгиз, 1959. 1118 с.
Публикации с ключевыми словами: трещина, собственная частота, волновое уравнение, точечный груз, изменение собственных частот
Публикации со словами: трещина, собственная частота, волновое уравнение, точечный груз, изменение собственных частот
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



