научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2012
УДК 623.52
МГТУ им. Н.Э. Баумана
Вычислительный центр им. А.А. Дородницына РАН
Введение
Одним из важнейших вопросов в развитии ствольного оружия является повышение начальной скорости снаряда. За последние десятилетия было предложено множество разнообразных схем, позволяющих тем или иным, как правило, достаточно экзотическим, способом получать высокие скорости снарядов [1]. Одним из таких способов является использование стволов переменного сечения. Исследования по внедрению цилиндроконических стволов активно проводились в 70-е – 80-е годы прошлого века, в частности, профессором В.С. Владимировым. Основная идея применения данного типа стволов, упрощенная схема которых показана на рис. 1, состоит в использовании гидродинамического эффекта, который достигается при пролете снаряда 1 вместе с пластическим поршнем 2 по дополнительному конусу 6, вызывающему пластическое деформирование как снаряда, так и поршня. За счет такого эффекта, материал снаряда и поршня испытывает дополнительное повышение скорости (эффект аналогичен разгону газа в сопле ракетных двигателей), в результате чего скорость на выходе из канала ствола может существенно превышать таковую для классических артиллерийских орудий.

Рис. 1 Упрощенная схема цилиндроконического ствола: 1 - снаряд, 2 – пластический поршень, 3 – инерционная масса, 4 – метательный заряд, 5 – затвор, 6 – дополнительный конус
В настоящей работе рассматриваются вопросы, связанные с физикой такого процесса, а также с методом численного моделирования, позволяющим рассчитывать сложные быстропротекающие процессы в стволах переменного сечения.
Следует отметить, что схожие исследования проводились на кафедре СМ-6 МГТУ им. Н.Э. Баумана в 70-х годах прошлого века, а также многими другими исследователями, которые решали вопросы газодинамического моделирования внутрибаллистических процессов. В частности, многие из изложенных ниже идей расчета были в той или иной мере опробованы еще в те годы. Однако, возможности вычислительных средств тех лет не позволяли производить точных расчетов, поэтому, в частности, приходилось брать достаточно крупные сетки, вводить дополнительные упрощения и т.п. В то же время современные средства математического моделирования внутренней баллистики [2] сосредоточены главным образом на точном решении задач анализа систем активного метания. При задачах синтеза основное внимание должно быть уделено простоте вычислительной модели при ее максимальной адекватности исследуемым процессам, что продиктовано необходимостью многократного прямого решения задачи (задача анализа) для определения оптимальных параметров системы. Именно в этом контексте предлагается использовать описанную в настоящей работе модель.
Внутренняя баллистика цилиндроконического ствола
Внутрибаллистические процессы в стволах переменного сечения обычно описываются при помощи квазиодномерных газодинамических уравнений с учетом тепло- и массоподвода в эйлеровых координатах [2]
 (1)
(1)
где u, ρ, p, ε - скорость, плотность, давление и внутренняя энергия газопороховой смеси, f - сила пороха, k - показатель адиабаты порохового газа, S - площадь поперечного сечения канала трубы, Jк – импульс конца горения пороха, z - относительная толщина сгоревшего свода порохового элемента, ψ - относительный объем сгоревшего пороха (функция газоприхода), α – коволюм (собственный объем молекул) единицы массы пороховых газов, δ - массовая плотность пороха, κ1, λ1 - коэффицинеты формы порохового зерна.
Однако, в работе [3] было показано, что для численного решения задач ствольного метания гораздо удобнее использовать массовые лагранжевы координаты. При этом под массовой лагранжевой координатой подразумевается масса, заключенная между двумя поперечными сечениями ствола с координатами x0 и x:
 или dm/dx = ρS (2)
или dm/dx = ρS (2)
Опуская подробные преобразование системы (1) при помощи замены (2), выпишем лишь окончательный результат
 (3)
(3)
При этом может быть поставлено два типа начальных и граничных условий.
1 тип. Отсчет времени с давления вспышки pвсп.
t = 0; 0 ≤ x ≤ Lкм: u = 0, p = pвсп, ρ = Δ, ψ = 0, z = 0.
t > 0; x = 0: u = 0 (абсолютно жесткая стенка).
t > 0; x = xт: dV / dt = (S pт – Rc)/q, u = V.
Здесь Lкм - длина каморы; Δ - плотность заряжания; V - скорость снаряда; q - масса снаряда; pт - разность давлений, которая действует на снаряд (индекс «т» означает метаемое тело); xт – координата метаемого тела; RC - сила сопротивления движению снаряда.
2 тип. Отсчет времени от давления форсирования pф.
t = 0, 0 ≤ x ≤ Lкм: u = 0, p = pф, ρ = Δ, ψ = ψф, z = zф.
t > 0, x = 0: u = 0 (абсолютно жесткая стенка).
t > 0, x = xт: dV / dt = (S pт – Rc)/q, u = V.
Здесь параметры с индексом «ф» относятся к моменту форсирования и определяются по известным формулам [2].
Для описания состояния пластического поршня, материалом которого может служить, например, полиэтилен высокого давления, можно использовать сокращенную систему уравнений (3)
du / dt = – S ∂p / ∂m, dx / dt = u, p = p(ρ). (4)
Последнее уравнение является уравнением состояния для пластического материала. Вариант постановки пластического поршня в канал ствола приведен на рис. 2.

Рис. 2 Схема постановки пластического поршня в трубу (поршень заштрихован как жидкость)
Слева от поршня находится метательный заряд, отделенный бесконечно тонкой тяжелой перегородкой, справа находится другая перегородка, которая может служить как метаемым телом, так и разделителем между поршнем и какой-либо другой средой.
Граничные условия для задачи течения жидкости являются смежными с граничными условиями для основной задачи внутренней баллистики и задаче о метании тела (или газа). Так, на левой границе жидкости будет выполняться равенство давлений пластического поршня pпп и метательного заряда pмз по обе стороны от перегородки. На правой границе, если она граничит со снарядом, pппS – Rc = m dV / dt, а если она граничит с какой-то другой сжимаемой средой, должно выполняться условие равенства давлений по обе стороны от границы раздела сред. Таким образом, все задачи являются сопряженными и не могут решаться отдельно.
Остановимся на вопросе выбора уравнения состояния. В работе [4] для полиэтилена высокого давления приведено следующее уравнение состояния, которое справедливо при уровне давлений до 8 ГПа:
p = B Rρ (Rρ – 1)/(C – Rρ)2 , (5)
где Rρ = ρ / ρ0 – начальная плотность материала; B, С – эмпирические константы, характеризующие свойства конкретного материала. Так, например для широко используемого на практике материала пластического поршня - полиэтилена высокого давления B = 1,19 ГПа; C = 1,73. Значения этих коэффициентов для некоторых сред, которые также можно использовать в качестве материалов пластических поршней, приведены в таблице 1.
Таблица 1
Константы в уравнении состояния пластического поршня для различных материалов [4]
Материал поршня | ρ0, кг/м3 | B, ГПа | C | Скорость звука, м/с |
Политэтилен | 920 | 1.19 | 1.73 | 1558 |
Парафин | 910 | 1.737 | 1.763 | 1810 |
Ацетон | 800 | 18.05 | 3.5 | 1900 |
Метиловый спирт | 800 | 10.37 | 3.0 | 1800 |
Этиловый спирт | 790 | 5.618 | 2.67 | 1600 |
Среди известных схем расчета задач газовой динамики достаточно простой и точной является разностная схема Неймана или «крест» [5]. На гладких решениях эта схема имеет локальную аппроксимацию второго порядка точности по пространственный и временной переменной O(Δt2 + Δx2), а на течениях с ударными волнами – первого порядка O(Δt + Δx). Шаблон такой схемы показан на рис. 3 – по вертикали отложены временные слои, по горизонтали – координатные.

Рис. 3 Шаблон схемы «крест»
Конечно-разностная аппроксимация системы уравнений внутренней баллистики в лагранжевой форме (3) по схеме «крест» имеет вид
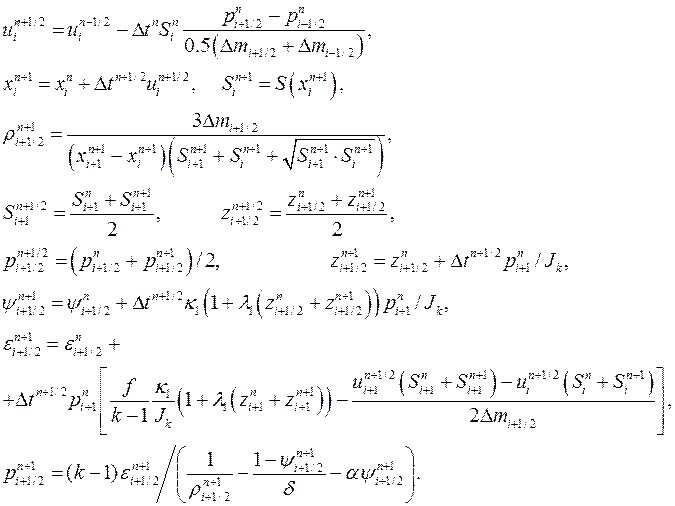 (6)
(6)
Шаги по времени на следующем временном слое вычисляются из условия устойчивости Куранта
 ,
,
где 0 < Ku ≤ 1 – число Куранта.
Шаг по координате и скорость звука определяются из соотношений
 .
.
Если Δtn+3/2 > 1.1 Δtn+1/2, то полагается
Δtn+3/2 = 1.1 Δtn+1/2, Δtn+1 = 0.5 (Δtn+3/2 + Δtn+1/2).
Этой схеме может быть дана следующая интерпретация. Заснарядный объем разбивается на N участков, в каждом из которых выполняется закон сохранения массы. При этом первое уравнение системы (6) можно интерпретировать как уравнение движения для тяжелой границы между двумя ячейками с массами Δmi+1/2 и Δmi–1/2, которой приписывается условная масса (Δmi+1/2 + Δmi–1/2)/2, под действием разности давлений в ячейках с номерами i + ½ и i – ½. Крайними массами являются масса затвора (который также может быть подвижным) и масса снаряда.
Как видно, для того, чтобы произвести расчет по системе (6), необходимо знать давление на следующем шаге по времени. Для решения этого вопроса в работе [3] было предложено в первом приближении положить давление на следующем временном слое равным давлению на предыдущем, т.е. ![]() . Затем значения на рассматриваемом координатном слое уточняются путем итерационного повторения вычислений по системе (6) до сближения по давлению с заранее заданной степенью точности. При этом неявная схема превращается в явную с пересчетом.
. Затем значения на рассматриваемом координатном слое уточняются путем итерационного повторения вычислений по системе (6) до сближения по давлению с заранее заданной степенью точности. При этом неявная схема превращается в явную с пересчетом.
В том случае, если на очередном шаге по пространственной координате происходит попадание в область пластического поршня, следует вести расчет для данной ячейки по соответствующим разностным аппроксимациям уравнений для пластического поршня (4). При этом все аппроксимации остаются теми же, за исключением уравнения состояния
 .
.
численный Расчет цилиндроконического ствола
Расчет цилиндроконического ствола проводился на примере схемы, показанной на рис. 4.

Рис. 4 Расчетная схема бикалиберной установки
Параметры метаемой сборки:
масса поражающего элемента | q = 42 г, |
масса инерционного поддона | mип = 15 г, |
масса затвора | mзатв = 10 т, |
коэффициент фиктивности массы снаряда | φ = 1.688. |
Геометрия канала (рис. 4):
длина каморы | 250 мм, |
длина области пластического поршня | 150 мм, |
длина пути снаряда в разгонной части ствола | 1000 мм, |
диаметр каморы | 44 мм, |
диаметр разгонной части ствола | 30 мм, |
диаметр выходной части ствола | 14.5 мм, |
длина конического участка | 1000 мм. |
Параметры пороха 4/7 [1]:
сила пороха | f = 1.027 МДж/кг, |
импульс пороха | Jk = 0.32 МПа×с, |
плотность заряжания | Δ = 900 кг/м3 |
геометрия пороха | κ1 = 0.811, λ1 = 0.081, z = 1.488. |
Расчетные зависимости давления пластического поршня на дно снаряда и давления газопороховой смеси на дно канала ствола приведены на рис. 5.

Рис. 5. Кривые давления на дно канала (пунктирная линия) и на дно снаряда (сплошная линия)
Как видно из этих зависимостей, на дно канала приходится приблизительно стандартное для порохового выстрела распределение давления. В то же время давление на дно снаряда характеризуется сильным пиком в районе 3.5 мс, который как раз отражает прохождение снаряда с пластическим поршнем через конический участок ствола (более тщательный анализ показывает наличие двух пиков, каждый из которых связан с геометрическими переходами между цилиндром и конусом и наоборот). Из этого следует, что кроме положительных свойств, выражающихся в ускорении снаряда, этот процесс имеет и отрицательные свойства, заключающиеся в местном повышении давления внутри конического участка, что должно вести к быстрому его износу.
На рис. 6 приведена зависимость скорости метаемого тела от времени. Участок резкого повышения скорости снаряда между моментами времени 2,8 мс и 3,4 мс отвечает прохождению пластического снаряда через конический участок. Геометрия ствола в данной расчетной схеме выбрана таким образом, чтобы снаряд мог набрать предельную «классическую» скорость перед достижением конического участка.
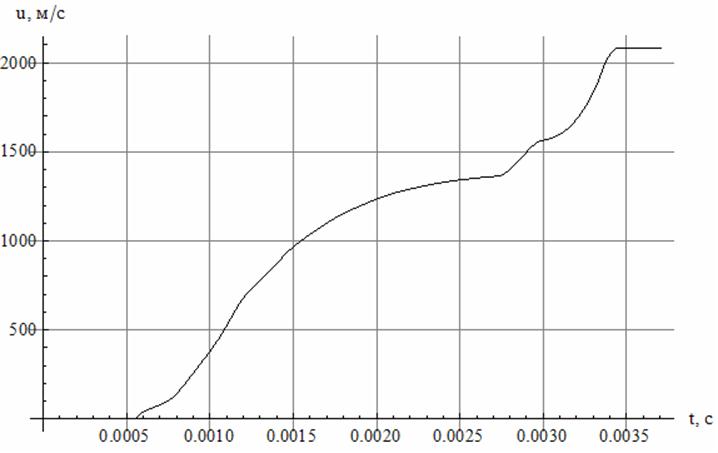
Рис. 6 Скорость снаряда в канале ствола
Таким образом видно, что наличие конического участка позволяет увеличить скорость с 1350 м/с, характерной для классических схем, до 2100 м/с, то есть более, чем в полтора раза.
Заключение
Приведенные результаты по численному моделированию метательной установки с цилиндроконическим стволом с одной стороны показывают перспективность подобных систем – как видно из сравнения начальных скоростей снарядов классической артиллерийской и бикалиберной систем, при прочих равных параметрах бикалиберная система имеет выигрыш в начальной скорости. С другой стороны следует помнить об уже отмеченном выше существенном недостатке подобных систем – в области переходного конуса создается повышенное давление, что может привести к интенсивному изнашиванию этой части. Этот недостаток, разумеется, не является препятствием для создания данного типа метательных установок, он может быть устранен с помощью различных конструктивных мероприятий, которые, впрочем, требуют дополнительных затрат ресурсов.
Что касается рассмотренной математической модели, то следует подчеркнуть ее универсальность. Эта модель позволяет рассчитывать как классические схемы, так и схемы с достаточно сложной компоновкой сред внутри ствола: с пластическими материалами, с легким газом, с взрывчатыми веществами, а также комбинациями из этих сред.
Рассмотренная в работе методика позволяет рассчитывать и более сложные конфигурации [6].
Литература
1. Физические основы устройства и функционирования стрелково-пушечного, артиллерийского и ракетного оружия. Часть 1. Физические основы устройства и функционирования стрелково-пушечного и артиллерийского оружия / Под ред. А.А. Королева и В.Г. Кучерова; ВолГТУ. – Волгоград, 2002. – 560 с.
2. Хоменко Ю.П., Ищенко А.Н., Касимов В.З. Математическое моделирование внутрибаллистических процессов в ствольных системах. – Новосибирск: Издательство СО РАН, 1999. – 256 с.
3. Юрышев Ю.А., Владимиров В.С. Использование лагранжевых координат для моделирования процессов в баллистических установках // Труды МВТУ. – 1988. - №521, с.51-69.
4. Физика взрыва / Под ред. Л.П. Орленко. – Изд. 3-е. – в 2 т. Т.2. – М.: Физматлит, 2002. – 656 с.
5. Бахвалов Н.С. и др. Численные методы / Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. – 5-е изд. – М.: БИНОМ. Лаборатория знаний, 2007. – 636 с.
6. Быков Н.В., Владимиров В.С., Зеленцов В.В. Инженерная методика расчета внутренней баллистики систем высокоскоростного метания // Оборонная техника, 2011, №8, с.3-9.
Публикации с ключевыми словами: численное моделирование, цилиндроконические стволы, внутренняя баллистика, активное метание пластических тел
Публикации со словами: численное моделирование, цилиндроконические стволы, внутренняя баллистика, активное метание пластических тел
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



