научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2012
УДК 535.015
МГТУ имени Н.Э. Баумана
В настоящее время наиболее перспективным направлением в волоконно-оптических системах связи (передачи информации) является использование оптических солитонов Это обусловлено тем, что световые импульсы в виде солитона сохраняют свою форму (cеканс гиперболический) [1, 2, 3]. Форма оптического солитона определяется в нелинейной среде балансом между двумя конкурирующим процессами: дисперсионным расплыванием светового импульса (то есть хроматическая дисперсия) и фазовой самомодуляцией (ФСМ), возникающей из-за нелинейности среды распространения оптического сигнала.
Хроматическая дисперсия возникает вследствие того, что составляющие оптического спектра импульса распространяются со слегка отличными друг от друга групповыми скоростями, что является главной причиной расширения импульса. Вклад в хроматическую дисперсию вносят два механизма: материальная и волноводная дисперсии. Хроматическая дисперсия приводит к расширению светового импульса без изменения его спектра.
Причина возникновения ФСМ обусловлена эффектом Керра, который возникает из-за высокой плотности энергии, проходящей по сердечнику одномодового волокна: ![]() , где эффективное значение интенсивности
, где эффективное значение интенсивности 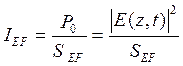 определяется отношением пиковой мощности импульса
определяется отношением пиковой мощности импульса ![]() к эффективной площади моды
к эффективной площади моды ![]() , где
, где ![]() – медленно меняющаяся амплитуда (огибающая) светового импульса [4].
– медленно меняющаяся амплитуда (огибающая) светового импульса [4].
Для упрощения математического анализа, рассмотрен гауссовый импульс вместо секанса гиперболического, поступающий на входной торец волокна. Видно, что импульс при распространении в волокне изменяет показатель преломления сердечника волокна и на расстоянии z приобретает дополнительный фазовый набег ![]() , что приводит к расширению спектра импульса в результате ФСМ.
, что приводит к расширению спектра импульса в результате ФСМ.
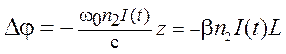
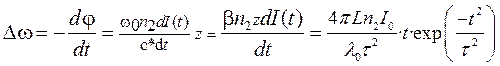
Величина и знак частотного сдвига оптического сигнала определяются производной от его огибающей (рис. 1). На языке длин волн это соответствует тому, что коротковолновые спектральные компоненты располагаются на переднем фронте, а длинноволновые − в хвосте. Это означает, что первоначально спектрально ограниченный импульс приобретает частотную модуляцию и ширина его спектра увеличивается. Учитывая зависимость групповой скорости сигнала от частоты спектра, можно сделать вывод, что у длинноволновых компонент спектра скорость распространения больше, чем у коротковолновых, что приводит к тому, что огибающая заднего фронта импульса распространяется с большей скоростью, чем огибающая переднего фронта. Это приводит к сужению передаваемого сигнала.
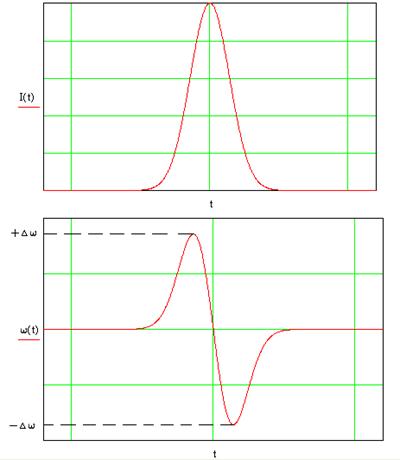
Рис. 1. Огибающая оптического сигнала и производная от нее
При качественном анализе совместного действия ФСМ и дисперсия рассматриваются как последовательные процессы. Характер преобразования показан на рис. 2.
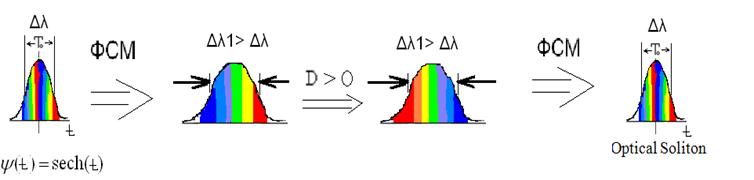
Рис. 2. Качественный анализ совместного действия ФСМ и дисперсии
1) ФСМ увеличивает спектральную ширину импульса и придает ему отрицательную частотную модуляцию. Передний фронт сдвигается в длинноволновую область, а спад – в коротковолновую.
2) Под действием положительной дисперсии длинноволновые компоненты отстают от коротковолновых. Если величина дисперсии подобрана правильно, то коротковолновые компоненты переместятся на передний фронт импульса, а длинноволновые на спад.
3) При повторном воздействии нелинейности ФСМ сдвигает коротковолновый фронт в длинноволновую область, а длинноволновый спад в коротковолновую область.
В результате формируется сигнал первоначально спектрального состава. Такой режим соответствует точному балансу действия эффектов дисперсии и ФСМ.
Флуктуации времени прихода солитонов.
В солитонных системах связи необходимо иметь ввиду существование флуктуации времени прихода солитона на ПУ, вследствие случайного характера разности фаз между солитонами, следующими друг за другом [5]. Это приводит к изменению периода их распространения, при этом если разность фаз удовлетворяет условию, 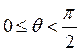 , то два солитона в процессе распространения сближаются и сталкиваются (рис. 3) [6, 7]. Для упрощения математического анализа, рассмотрен гауссовый импульс. Длина столкновения двух гауссовых сигналов, распространяющихся подобно солитонам, определяется следующим выражением [8, 9]:
, то два солитона в процессе распространения сближаются и сталкиваются (рис. 3) [6, 7]. Для упрощения математического анализа, рассмотрен гауссовый импульс. Длина столкновения двух гауссовых сигналов, распространяющихся подобно солитонам, определяется следующим выражением [8, 9]:
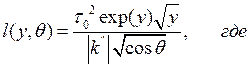
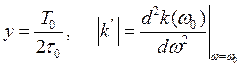 ,
,
где ![]() - полуширина солитона;
- полуширина солитона; ![]() - период солитонов;
- период солитонов; ![]() -постоянная распространения основной моды;
-постоянная распространения основной моды; ![]() -разность фаз между двумя соседними солитонами.
-разность фаз между двумя соседними солитонами.
Выражение справедливо для скважности сигнала ![]() .
.
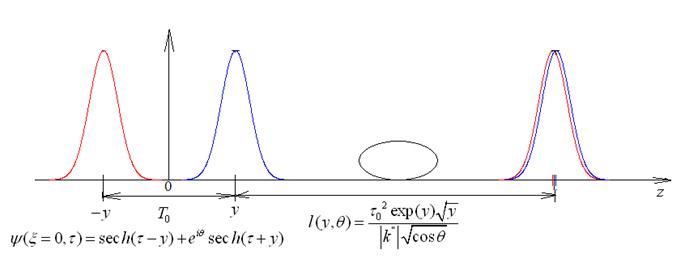
Рис. 3. Иллюстрация сближения и столкновения двух солитонов
При равномерном законе распределения разности фаз в рассматриваемой области их значений величина изменения (уменьшения) периода следования солитонов в некоторой точке z: 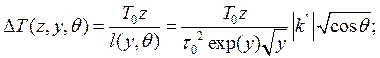 определены среднее значение (математическое ожидание)
определены среднее значение (математическое ожидание) ![]() и дисперсия
и дисперсия ![]() изменения (уменьшения) периода следования солитонов в некоторой точке z при условии, что случайная величина
изменения (уменьшения) периода следования солитонов в некоторой точке z при условии, что случайная величина ![]() - разность фаз, равномерно распределена в интервале
- разность фаз, равномерно распределена в интервале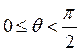 (рис. 4).
(рис. 4).
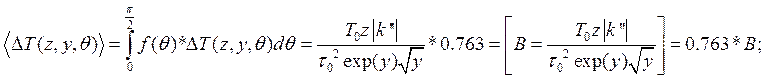
![]()
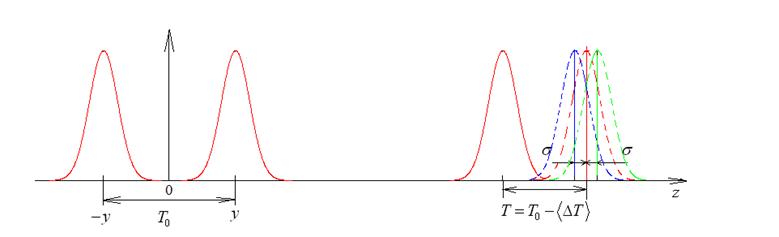
Рис. 4. Иллюстрация сближения двух солитонов
В предположении гауссовой формы огибающей солитона![]()
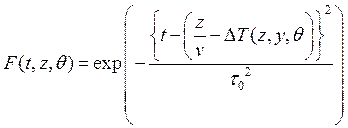
и в соответствии со сказанным выше, время прихода солитонов в некоторую точку z, где расположен ПИ, будет случайным (рис. 5). Тогда среднее значение ![]() и дисперсия
и дисперсия ![]() сигнала в точке приема z определяется как
сигнала в точке приема z определяется как
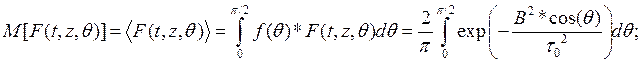
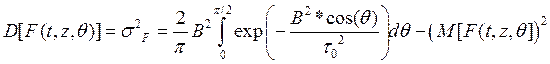
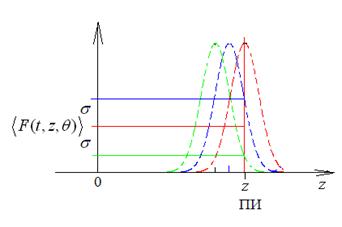
Рис. 5. Иллюстрация случайного характера прихода солитона в точку z (ПИ)
Дисперсию необходимо учитывать в солитонных ВОСП при расчете отношения сигнал/шум и вероятности ошибок.
Рэлеевское рассеяние в одномодовом волокне.
В оптических волокнах солитоны, сохраняя свою форму, претерпевают энергетические потери, основной вклад в которые вносит рэлеевское рассеяние. Определим ту часть рассеянного излучения, которая распространяется в направлении обратном к передаваемому сигналу (к входному торцу оптоволокна). На рис. 6 представлена схема, в которой наблюдается обратное рэлеевское рассеяние. Рассеянное излучение измеряется приемником излучения ПИ1.
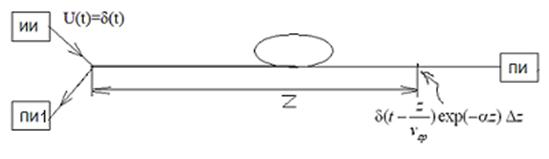
Рис. 6. Схема для расчета обратного рэлеевского рассеяния
Рассмотрено два вида входных сигналов: дельта функция Дирака и гауссова функция.
Для дельта функции ![]() временная характеристика рэлеевского рассеяния
временная характеристика рэлеевского рассеяния ![]() , АЧХ
, АЧХ ![]() и ФЧХ
и ФЧХ ![]() имеют следующий вид соответственно:
имеют следующий вид соответственно:
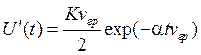 ;
;
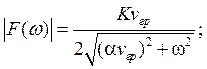
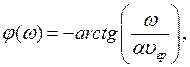
где![]() − часть обратно рассеянного рэлеевского излучения,
− часть обратно рассеянного рэлеевского излучения, ![]() − групповая скорость импульса,
− групповая скорость импульса, ![]() − коэффициент потерь.
− коэффициент потерь.
Для гауссового сигнала 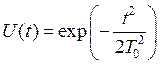 временная характеристика рэлеевского рассеяния
временная характеристика рэлеевского рассеяния ![]() , АЧХ
, АЧХ ![]() и ФЧХ
и ФЧХ ![]() имеют следующий вид соответственно:
имеют следующий вид соответственно:
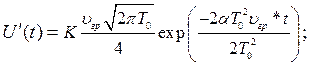
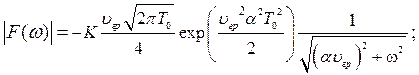
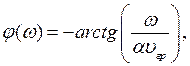
где![]() − коэффициент, характеризующий величину обратно рассеянного рэлеевского излучения,
− коэффициент, характеризующий величину обратно рассеянного рэлеевского излучения, ![]() − групповая скорость импульса,
− групповая скорость импульса, ![]() − коэффициент потерь.
− коэффициент потерь.
Из полученных соотношений можно сделать важный вывод о том, что вне зависимости от вида импульса на входе ВОЛС АЧХ и ФЧХ рэлеевского рассеянного излучения описываются идентичными соотношениями, а временная характеристика имеет вид убывающей экспоненты (рис. 7).
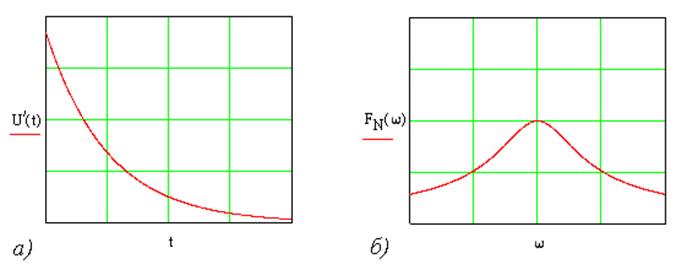
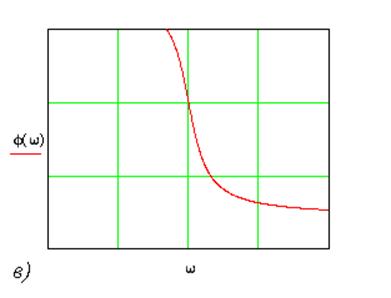
Рис. 7. а) временная характеристика рэлеевского рассеяния. б) АЧХ рэлеевского рассеяния. в) ФЧХ рэлеевского рассеяния.
В работе проведен анализ физики процесса возникновения оптического солитона за счет баланса двух физических конкурирующих процессов: дисперсионного расплывания светового импульса и ФСМ, возникающей из-за нелинейности среды распространения оптического сигнала. Сделан вывод, что использование оптических солитонов повышает широкополостность линии передачи, но при этом необходимо учитывать неизбежные потери, основной вклад в которые вносит рэлеевское рассеяние.
Литература
1. Hasegava A. Optical Solitons In Fibers. Berlin: Springer, 1989.
2. Mollenauer L. F., Gordon J. P. // IEEE J. Quantum Electron. 1986. Vol. 22. p. 157.
3. Ахманов С.А., Выслоух В.А., Чиркин А.С. // Успехи физических наук.−1986.− том 149.
4. Kivshar Y.S., Agrawal G.P. Optical Solitons from Fibers to Photonic Crystals, Academic Press, 2003.
5. Кившарь Ю.С., Агравал Г.П. Оптические солитоны, Москва, Физматлит 2005.
6. Выслоух В.А., Мишнаевский П.А. Взаимодействие солитонов в одномодовых волоконных световодах; роль возмущающих факторов, Радиофизика, том ХХХI, №7,1988.
7. Выслоух В.А., Мишнаевский П.А. Ширина полосы частот при передаче информации по оптическому волокну с помощью солитонов // Электросвязь, №3, 1988.
8. Hasegawa А., Таррег F. // Appl. Phys. Lett., 1973, v.23, р.142.
9. MollenauerL.F., Stolen А.Н., GordonJ.P. Phys. Rev. Lett., 1980, v.45, р.1095.
Публикации с ключевыми словами: оптическое волокно, солитон, дисперсия, эффект Керра, фазовая самомодуляция, рэлеевское рассеяние
Публикации со словами: оптическое волокно, солитон, дисперсия, эффект Керра, фазовая самомодуляция, рэлеевское рассеяние
Смотри также:
- Расчет волоконной брэгговской решетки в качестве демультиплексора в мультиплексированной линии связи
- Методика изложение темы «Случайные величины» в курсе «Теория вероятностей»
- Анализ дисперсионных характеристик погонных параметров элементарных отрезков сверхширокополосных балансных печатных щелевых антенн бегущей волны
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



