научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК.621
МГТУ им. Н.Э. Баумана
Введение
В настоящее время широкое распространение получают системы автономного жизнеобеспечения на различных обособленных объектах. В частности, автономной является система водоснабжения.
Простой пример системы автономного водоснабжения изображен на рис. 1.

Рис. 1. Система автономного водоснабжения включающая в себя гидроаккумулятор
Основными элементами системы автономного водоснабжения являются: погружной насос, гидроаккумулятор, блок автоматического управления с реле давления и соединительные трубы. Объектом настоящего исследования является гидроаккумулятор.
Гидроаккумулятор – это железный бак, внутри которого находится резиновая оболочка. Снаружи резиновой оболочки и внутри железного бака находится сжатый газ. Внутрь резиновой оболочки поступает под давлением вода из скважины. Поступление воды из скважины, т.е. включение насоса, происходит только тогда, когда давление воды в резиновой оболочке упадет до определенного уровня, определяющего момент включения насоса ![]() . Когда давление воды достигнет уровня
. Когда давление воды достигнет уровня ![]() , тогда насос прекращает свою работу и сжатый газ начинает выталкивать воду из резиновой оболочки. Таким образом, происходит поддержание давления воды в системе водоснабжения.
, тогда насос прекращает свою работу и сжатый газ начинает выталкивать воду из резиновой оболочки. Таким образом, происходит поддержание давления воды в системе водоснабжения.
Объем воды в резиновой оболочке, соответствующий давлению воды ![]() –
– ![]() , соответствующий давлению воды
, соответствующий давлению воды ![]() –
– ![]() . Тогда полезным или запасенным объемом воды в гидроаккумуляторе
. Тогда полезным или запасенным объемом воды в гидроаккумуляторе ![]() будет называться разница объемов воды
будет называться разница объемов воды ![]() и
и ![]() :
:
![]() .
.
Гидроаккумулятор позволяет увеличивать ресурс работы насоса.
Подбор параметров ![]() и
и ![]() , а также
, а также ![]() , давления газа внутри бака гидроаккумулятора, при фиксированном объеме железного бака
, давления газа внутри бака гидроаккумулятора, при фиксированном объеме железного бака ![]() , позволяет отыскать оптимальный режим работы гидроаккумулятора. Оптимальными режимами могут быть режимы, когда количество включений насоса за определенный период времени – минимально, при этом максимальным является полезный объем воды в гидроаккумуляторе и увеличивается ресурс работы насоса, и когда перепад давления воды в системе – минимальный, в этом случае, из водяных кранов вода течет с наибольшим напором.
, позволяет отыскать оптимальный режим работы гидроаккумулятора. Оптимальными режимами могут быть режимы, когда количество включений насоса за определенный период времени – минимально, при этом максимальным является полезный объем воды в гидроаккумуляторе и увеличивается ресурс работы насоса, и когда перепад давления воды в системе – минимальный, в этом случае, из водяных кранов вода течет с наибольшим напором.
Ведущие производители гидроаккумуляторов, такие как Reflex (Германия), Wester(Россия), Varem (Италия) и Джилекс (Россия), предлагают пользователям своих изделий, инструкцию для настройки гидроаккумулятора на оптимальный режим работы. Один из пунктов такой инструкции – это таблица, в которой предлагается перечень режимов с значениями ![]() и
и ![]() и, соответствующий режиму, – полезный объем воды в гидроаккумуляторе
и, соответствующий режиму, – полезный объем воды в гидроаккумуляторе ![]() .
.
Цель настоящей статьи – это разработка математической модели работы гидроаккумулятора, позволяющей численно, а не экспериментально, определить все режимы работы гидроаккумулятора. Т.е. численно определить зависимость между управляющими параметрами ![]() и
и ![]() и полезным объемом воды в гидроаккумуляторе –
и полезным объемом воды в гидроаккумуляторе – ![]() .
.
Разработанная методика расчета может быть полезна не только пользователю гидроаккумулятора, но и производителю, дабы производитель мог не тратить лишние денежные средства на проведение экспериментов при различных режимах работы.
В таблице ниже приведем экспериментальные данные исследования полезного объема воды в гидроаккумуляторе в зависимости от управляющих параметров.
Таблица
Экспериментальные данные исследования полезного объема воды в гидроаккумуляторе в зависимости от управляющих параметров
Номер замера | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Давление включения насоса, атм. | ||||||||||||||
| 1.5 | 1.5 | 2 | 2 | 2 | 2.5 | 2.5 | 2.5 | 3 | 3 | 3 | 4 | 4 | 5 |
Давление выключения насоса, атм. | ||||||||||||||
| 2.5 | 3 | 3 | 3.5 | 4 | 3.5 | 4 | 4.5 | 4 | 4.5 | 5 | 6 | 7 | 7.5 |
Объем бака, литр | Полезный объем воды в баке, литр | |||||||||||||
24 | 6.3 | 8.3 | 5.6 | 6.3 | 9 | 5 | 6.8 | 8 | 4.6 | 5.7 | 7.2 | 6 | 8.3 | 6.2 |
50 | 15 | 20 | 14 | 15 | 22 | 12 | 17 | 20 | 11 | 15 | 19 | 16 | 21 | 17 |
80 | 21 | 27 | 18 | 21 | 29 | 16 | 22 | 27 | 15 | 20 | 25 | 21 | 28 | 22 |
В результате исследования, сравним полученные результаты с экспериментальными данными и тем самым оценим правильность созданной математической модели работы гидроаккумулятора.
Основные уравнения для решения задачи
Объектом исследования в данной задаче является резиновая оболочка. Изобразим на рис. 2 резиновую оболочку внутри гидроаккумулятора в текущий момент времени.

Рис. 2. Состояние резиновой оболочки в текущий момент времени
Соответственно оболочка в текущий момент времени характеризуется следующими параметрами: ![]() – давление воды в оболочке;
– давление воды в оболочке; ![]() – объем воды в оболочке;
– объем воды в оболочке; ![]() ,
, ![]() – давление и объем газа в баке гидроаккумулятора.
– давление и объем газа в баке гидроаккумулятора.
По мере того, как оболочка наполняется водой, газ в баке гидроаккумулятора сжимается. Соответственно для изменения состояния газа можно записать уравнение изотермического сжатия
![]() (1)
(1)
где ![]() – количество моль газа, моль,
– количество моль газа, моль,
![]() – универсальная газовая постоянная,
– универсальная газовая постоянная, ![]() ,
,
![]() – температура газа, К.
– температура газа, К.
Тогда из соотношения выразим давление газа в текущий момент времени:
 (2)
(2)
Для текущих и начальных объемов воды и газа можно записать соотношение
![]() (3)
(3)
Тогда выражение с учетом выражения можно переписать следующим образом:
 (4)
(4)
Если рассмотреть резиновую оболочку в момент времени непосредственно перед включением насоса, то текущее значение давления воды в оболочке станет равным начальному, ![]() и в силу состояния равновесия оболочки
и в силу состояния равновесия оболочки ![]() . Тогда формула изменится:
. Тогда формула изменится:
 (5)
(5)
Таким образом, резиновая оболочка подвержена действию изнутри – давления воды ![]() , снаружи – давления газа
, снаружи – давления газа ![]() (рис. 2).
(рис. 2).
Для того, чтобы определить результирующую величину давления, действующего на резиновую оболочку, разложим нагрузку на симметричную и кососимметричную составляющие (рис. 3).

Рис. 3. Разложение нагрузки на симметричную и кососимметричную составляющие
На рис. 3 (1) – это симметричная составляющая нагрузки, (2) – это кососимметричная составляющая нагрузки.
Поскольку резина – материал несжимаемый, то симметричное нагружение не влияет на деформированное состояние резиновой оболочки. Т.е. оболочка подвержена действию только давления ![]() равного
равного
![]() . (6)
. (6)
И с учетом выражения выражение будет иметь вид
 ,
,
 . (7)
. (7)
Из выражения следует, что давление ![]() меняется в пределах от
меняется в пределах от ![]() до
до ![]() и объем воды
и объем воды ![]() меняется в пределах от
меняется в пределах от ![]() до
до ![]() , причем значения
, причем значения ![]() ,
, ![]() ,
, ![]() известны. Т.е. неизвестным является объем воды в резиновой оболочке
известны. Т.е. неизвестным является объем воды в резиновой оболочке ![]() в момент времени, когда давление воды равно
в момент времени, когда давление воды равно ![]() . Определив из уравнения объем воды
. Определив из уравнения объем воды ![]() , можно подсчитать полезный объем воды:
, можно подсчитать полезный объем воды:
![]() . (8)
. (8)
Но для решения уравнения необходимо определить зависимость давления ![]() от
от ![]() :
:
![]() – ? (9)
– ? (9)
Для решения задачи необходимо рассмотреть напряженно-деформированное состояние резиновой оболочки, нагруженной внутренним давлением ![]() .
.
На рис. 4 изобразим исходное и деформированное состояние резиновой оболочки и покажем геометрические параметры и силовые факторы оболочки.

Рис. 4. Исходное и деформированное состояние оболочки. Геометрические параметры и силовые факторы оболочки
На рис. 4 имеем:
![]() – радиус кривизны меридианального сечения оболочки,
– радиус кривизны меридианального сечения оболочки,
![]() – радиус кривизны нормального сечения, перпендикулярного меридиану,
– радиус кривизны нормального сечения, перпендикулярного меридиану,
![]() – угол между нормалью к меридиану и вертикальной осью,
– угол между нормалью к меридиану и вертикальной осью,
![]() – текущий радиус точки меридиана оболочки,
– текущий радиус точки меридиана оболочки,
![]() – дуговая координата меридиана оболочки,
– дуговая координата меридиана оболочки,
![]() – меридиональная интенсивность напряжений,
– меридиональная интенсивность напряжений,
![]() – окружная интенсивность напряжений,
– окружная интенсивность напряжений,
![]() – параметр, характеризующий деформированное состояние оболочки.
– параметр, характеризующий деформированное состояние оболочки.
Решение задачи будем проводить на основе теории мягких оболочек [1].
Далее приведем систему уравнений, к которой сводится решение задачи :
 (10)
(10)
где ![]() – степени удлинения,
– степени удлинения,
![]() – начальная толщина оболочки.
– начальная толщина оболочки.
Численное решение уравнений и дает нам дискретную зависимость ![]() . Т.е. решение системы уравнений позволяет затем решить уравнение и определить полезный объем гидроаккумулятора по формуле .
. Т.е. решение системы уравнений позволяет затем решить уравнение и определить полезный объем гидроаккумулятора по формуле .
Результаты решения задачи
Для более наглядного представления результатов решения задачи, введем нормирование параметров резиновой оболочки:
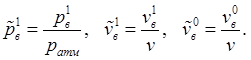
По этим формулам пересчитаем экспериментальные данные для гидроаккумулятора с баком объемом ![]() литр., представленные в таблице выше, и построим на графике точки, соответствующие каждому режиму (рис. 5).
литр., представленные в таблице выше, и построим на графике точки, соответствующие каждому режиму (рис. 5).
Линиями на графике соединим экспериментальные точки, дабы проследить подобие экспериментальных и расчетных данных.
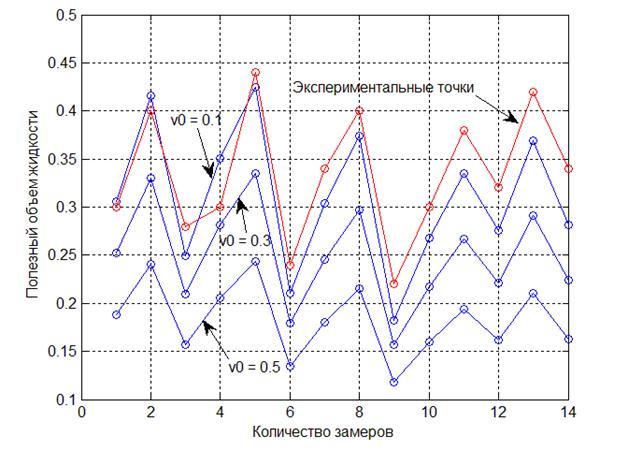
Рис. 5. Сравнение результатов численного решения с экспериментальными данными
На рис. 5 ![]() – это безразмерный начальный объем воды в оболочке
– это безразмерный начальный объем воды в оболочке ![]() .
.
Из графиков видно, что результаты расчетов подобны экспериментальным данным. Т.е. созданная математическая модель верно описывает процесс работы гидроаккумулятора.
Также из рис. 5 видно, что чем меньше начальный объем воды, тем больше полезного объема воды запасает гидроаккумулятор.
Таким образом, с помощью разработанной математической модели можно получить величину полезного объема в зависимости от любых режимов работы гидроаккумулятора.
Т.е. используя созданную математическую модель можно подбирать наиболее оптимальные режимы работа насоса. Например, для увеличения ресурса работы насоса, следует настроить гидроаккумулятор так, чтобы он выдавал наибольший полезный объем воды, тогда насос в системе водоснабжения будет работать реже.
Этот вывод иллюстрирует поверхность полезного объема воды в гидроаккумуляторе на рис. 6.

Рис. 6. Поверхность изменения полезного объема в зависимости от регулируемых давлений
На рис. 6 ![]() – это давление воды в оболочке, при котором включается насос
– это давление воды в оболочке, при котором включается насос ![]() ,
, ![]() – это давление воды в оболочке, при котором выключается насос
– это давление воды в оболочке, при котором выключается насос ![]() и
и ![]() – это полезный объем воды
– это полезный объем воды ![]() .
.
Выводы
Таким образом, разработанная математическая модель позволяет проводить численные эксперименты вместо реальных, а также позволяет пользователю гидроаккумулятора, без лишних проблем настроить на оптимальную работу свой конкретный гидроаккумулятор.
Библиографический список:
1. Бидерман В.Л. Механика тонкостенных конструкций. Статика, – М.: Машиностроение, 1977. – 488 с.
2. Пономарев С.Д. и др., Расчеты на прочность в машиностроении. – М.: Машгиз, 1958. – Т. 1. – 680 с.
Публикации с ключевыми словами: гидроаккумулятор, уравнение состояния идеального газа, теория мягких оболочек
Публикации со словами: гидроаккумулятор, уравнение состояния идеального газа, теория мягких оболочек
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



