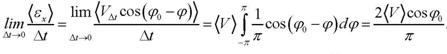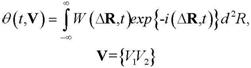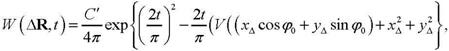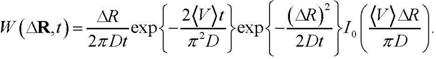научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 621.396
МГТУ им. Н.Э.Баумана
Улучшение показателей скрытности сигналов радиоэлектронных систем (РЭС) может обеспечиваться многими способами и средствами. В частности, изменениями параметров (пространственно-временных) маскируемых сигналов. Ниже, в этой статье, рассматривается задача оптимизации стратегии пространственного маневрирования источников сигналов, информативных для средств радио- и радиоэлектронных разведок (РРТР). Такого маневрирования пространственными параметрами маскируемых сигналов, которое снижает их заметность (улучшает скрытность).
Для подвижного (маневрирующего в пространстве) объекта сеанс работы с излучением сигнала произойдет не ранее, чем через длительность паузы tп, во время которой происходит маневр перемещения из точки с координатами Riв позиционном районе в точку Ri+1ÎR3. Перемещение объекта происходит со скоростью V. Ориентация и модуль вектора скорости определяются тактическими и техническими соображениями, а также свойствами дорожной сети в районе маневрирования. Во всяком случае, для средства РРТР направления возможного перемещения объекта из точки проведения сеанса Ri равновероятны почти всегда, кроме, может быть, точек в непосредственной близости к границам позиционного района (маневр из этих точек имеет преимущественное направление внутрь области R3). Модуль и направление вектора скорости будут меняться в процессе совершения маневра смены позиции. При этом естественно считать, что модуль вектора скорости движения объекта ограничен.
После окончания сеанса работы на излучение, когда объект с вероятностью Ридн обнаруживается средством разведки и когда определяются координаты его местоположения Ri, для разведчика наступает ситуация вторичного поиска (поиска по вызову). При любом способе и алгоритме вторичного поиска его качественные характеристики будут определяться в том числе и плотностью распределения априорной вероятности нахождения объекта в каждый момент времени в данной точке R позиционного района или области интересов разведки R3´F´Т. Эта же плотность может характеризовать качество маскировки объекта от обнаружения средствами разведки. Для дальнейшего определения плотности распределения вероятностей положения объекта в позиционном районе (априорной плотности распределения положения при вторичном поиске) принимаются следующие предположения.
1. Считается, что размерность геометрического подпространства области интересов разведки R2, т.е., что движение объекта в процессе маневрирования происходит на плоскости. При этом вектор смещения DR из точки начала маневра Ri определяется двумя проекциями XD и YD в координатной системе с началом в R.
2. К концу сеанса (или к началу маневра, которому предшествовало излучение сигнала) точка положения объекта может быть известна разведчику с точностью до малых ошибок. Поэтому плотность распределения вероятностей оценки разведчиком координат R* нормальная, дисперсия ошибки ![]() достаточно мала, так что "ширина" этой плотности по сравнению с "шириной" плотности вероятностей точки расположения объекта в конце маневра незначительна, и можно считать, что
достаточно мала, так что "ширина" этой плотности по сравнению с "шириной" плотности вероятностей точки расположения объекта в конце маневра незначительна, и можно считать, что
| (1) |
3. В процессе маневрирования объект изменяет направление и величину скорости движения чаще, чем за время tп паузы между сеансами, так что изменение координат объекта за время t складывается из довольно большого количества малых последовательных перемещений по различным направлениям.
4. Пространство R2 в позиционном районе изотропно, т.е., статистические характеристики вектора скорости движения объекта одинаковы и не зависят от координат RR2.
Итак, пусть в момент окончания сеанса излучения объект разведки начинает маневр в позиционном районе на плоскости R2. Плотность распределения вероятностей точки расположения объекта в произвольный момент времени t+Dt будет W(DR,t); DR={X,Y} вектор координат на плоскости, где по предположению совершается маневр; W(DR,t)Dt вероятность того, что за некоторый малый интервал времени Dt объект сместится в точку DR, пройдя малый путь e={ex,ey}. При этом неважно, какой именно отрезок пути e объект прошел за время Dt, т. е.
| (2) |
Для малых |e| можно разложить W(DR–e) в степенной ряд около DR и ограничиться членами разложения по порядку величины не более |e|2:
| (3) |
Подставляя (2) в (3), можно получить:
| (4) |
Или, разделив правую и левую части на Dt и переходя к пределу при Dt0, можно получить: во-первых,
| (5) |
из-за того, что направление вектора скорости в каждый момент времени можно принять равновероятным и, во-вторых,
| (6) |
В силу изотропности пространства позиционного района ![]() – это дисперсия разброса конца вектора e пути, пройденного объектом за время Dt. При любом ограниченном законе распределения проекций скорости движения объекта на координатные оси nx=nsin и ny=ncos дисперсии
– это дисперсия разброса конца вектора e пути, пройденного объектом за время Dt. При любом ограниченном законе распределения проекций скорости движения объекта на координатные оси nx=nsin и ny=ncos дисперсии ![]() и
и ![]() конечны. Для исключения физически некорректного предположения о возможности бесконечного перемещения объекта за конечное время, необходимо считать, что
конечны. Для исключения физически некорректного предположения о возможности бесконечного перемещения объекта за конечное время, необходимо считать, что ![]() и
и ![]() растут со временем не быстрее, чем линейно, т. е., что
растут со временем не быстрее, чем линейно, т. е., что ![]() . Однако достаточны будут предположения о постоянстве дисперсии разброса e, т.е. D=const(t). Это вытекает из предположения об изотропности пространства R2 (условия движения объекта при маневрировании всюду одинаковы, поэтому одинаковы и дисперсии длины пути за одинаковое время).
. Однако достаточны будут предположения о постоянстве дисперсии разброса e, т.е. D=const(t). Это вытекает из предположения об изотропности пространства R2 (условия движения объекта при маневрировании всюду одинаковы, поэтому одинаковы и дисперсии длины пути за одинаковое время).
В-третьих,
| (7) |
что означает очень малую вероятность больших смещений e за конечное время; ![]() убывает быстрее, чем стремится к нулю Dt.
убывает быстрее, чем стремится к нулю Dt.
Более высокие моменты <|e|n>; n>3 должны убывать еще быстрее. Учитывая (6), и (7) в (3) можно получить
| (8) |
где ![]() оператор Лапласа.
оператор Лапласа.
Дифференциальному уравнению (8) должна, при сделанных предположениях, удовлетворять плотность распределения вероятностей нахождения маневрирующего объекта в точке с координатами DR={XDYD} в момент времени t при условии, что в начальный момент t=0 координаты объекта были R0.
Уравнение (8) параболическое. Подобные уравнения встречаются в задачах теплопроводности [2]. Если не рассматривать для W(DR,t) условия на границах позиционного района (когда эти границы неизвестны разведчику или достаточно широки по сравнению с длиной пути, проходимого объектом между сеансами t=tп), для уравнения (8) может быть поставлена задача Коши с начальными условиями:
| (9) |
Решение этой задачи известно и представляется двумерным интегралом Пуассона ![]() или, с учетом нормировки W(DR,t) на всей плоскости {xD;yD},
или, с учетом нормировки W(DR,t) на всей плоскости {xD;yD},
| (10) |
Предположение об отличии начального распределения от d-функции несильно изменит результат: просто дисперсия текущей плотности W(DR,t) будет несколько больше, чем Dt за счет аддитивной составляющей дисперсии начального распределения W(DR).
Как видно из (10), даже довольно слабые предположения о тактике проведения маневра маскируемым объектом в позиционном районе приводят к выводу о том, что распределение вероятностей точки его расположения подчиняется нормальному закону. Среднее значение и мода распределения соответствует точке DR=0, т.е. точке, где был обнаружен объект по его излучению.
Распределение "расплывается" со временем из-за линейного роста дисперсии Dt. Скорость "расплывания" распределения тем больше, чем лучше динамические свойства объекта, чем больше максимальная скорость его движения от точки проведения сеанса. Графическая иллюстрация решения (10) представлена на рис.1.
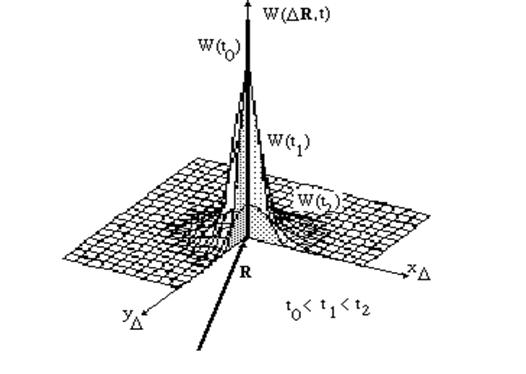
Рис.1. Априорная плотность при случайном маневрировании объекта разведки
в пространстве
Несколько иные предположения о характере маневра приводят к другим решениям. Эти предположения состоят в следующем. Пусть, как считалось и прежде, немедленно после окончания сеанса, в котором, возможно, объект был обнаружен, начинается маневр пространственного перемещения. В процессе совершения маневра объект смещается по направлению 0 из точки R0. Значение 0 противнику неизвестно; любые значения 0 для него равновероятны: ![]() . Но затем в процессе движения объект меняет направление вектора скорости не равновероятным образом, а так, чтобы как можно скорее и как можно дальше уйти от точки проведения сеанса.
. Но затем в процессе движения объект меняет направление вектора скорости не равновероятным образом, а так, чтобы как можно скорее и как можно дальше уйти от точки проведения сеанса.
Поскольку объект движется по дорогам, изменения модуля и направления скорости возможны, но аргумент вектора скорости уже не будет равновероятным в пределах 2p. Требования наиболее быстрой смены позиции на наиболее удаленную предполагает, что вектор скорости в процессе движения будет отклоняться от направления 0 не более, чем на острый угол. При таких условиях средние проекции смещения положения объекта в системе координат xDyD будут
| (11) |
В (11) считается, что распределены равномерно на интервале ![]() . Поэтому плотность распределения вероятностей:
. Поэтому плотность распределения вероятностей: ![]() . Аналогично
. Аналогично
| (12) |
Входящая в соотношения (11) и (12) величина ![]() это средняя скорость движения объекта разведки при маневрировании в позиционном районе.
это средняя скорость движения объекта разведки при маневрировании в позиционном районе.
Временные производные вторых моментов (коэффициенты диффузии) определяются как и (6):
| (13) |
| (14) |
| (15) |
Поэтому соотношение (5) не изменит своего вида и в этом случае. С учетом соотношений (11) (15) уравнение для плотности распределения вероятностей W(DR,t) примет вид
| (16) |
Это линейное однородное уравнение параболического типа, чаще всего рассматриваемое при решении задач исследования диффузии. Введением характеристической функции плотности распределения
| (17) |
уравнение (17) приводится к обыкновенному дифференциальному уравнению первого порядка. Действительно, поскольку q(t,V) является двумерным преобразованием Фурье плотности W(DR,t) по пространственным переменным xDyDR,
| (18) |
из (17) непосредственно следует, что
| (19) |
| (20) |
| (21) |
Переходя в (17) от W(DR,t) к q(t,V) и используя соотношения (18), (19) и (20), ![]() можно получить
можно получить
| (22) |
откуда
| (23) |
где C постоянная интегрирования, в конкретизации которой нет необходимости на данном этапе решения.
Переходя при помощи обратного преобразования Фурье от q(t,V) к плотности распределения вероятностей координат объекта, можно получить
| (24) |
Квадратичная форма в показателе экспоненты под интегралом заменой переменных может быть преобразована к виду u1+u2,
| (25) |
а (24) записано как
| (26) |
где ![]() новая постоянная интегрирования.
новая постоянная интегрирования.
Интегрирование (26) приводит к выражению для искомой плотности распределения вероятностей
| (27) |
в которой C' естественным образом определяется из условия нормировки. Считая размеры позиционного района очень большими по сравнению с "шириной" плотности распределения вероятностей положения объекта, условие нормировки можно представить в виде
| (28) |
откуда
| (29) |
И окончательная форма для плотности распределения вероятностей точки нахождения объекта разведки в момент времени t при начальном распределении
| (30) |
представляется как
| (31) |
Преобразуя квадратичную форму показателя экспоненты в (31), можно получить
| (32) |
где применена подстановка:
![]() модуль вектора DR математического ожидания положения маскируемого объекта на плоскости xDyD;
модуль вектора DR математического ожидания положения маскируемого объекта на плоскости xDyD;
![]() аргумент вектора DR.
аргумент вектора DR.
При выводе окончательной формы (32) была использована теорема косинусов. С учетом (32) и нормировки при [0;2p], DR[0:] плотность распределения вероятностей представляется в виде
| (33) |
Графическая интерпретация плотности распределения вероятностей мгновенного положения маневрирующего объекта (31) и (32) приведена на рис.2.
Как видно из рис.2, по мере увеличения времени t после начала маневра в момент t=0, нормальная плотность W(R,t) линейно смещается из точки R0 (той точки, где xD=yD=0) на величину ![]() по направлению 0 и "расплывается", линейно увеличивая дисперсию по закону
по направлению 0 и "расплывается", линейно увеличивая дисперсию по закону ![]() .
.

Рис.2. Априорная плотность при движении объекта разведки по дорогам
в районе маневрирования
Найденная таким образом плотность является, по сути, условной W(DR,t|0) при том условии, что движение в процессе маневрирования маскируемого объекта совершается по преимущественному направлению 0. Но направление 0 для противника случайно. Поэтому безусловная плотность распределения вероятностей мгновенного положения объекта на плоскости в позиционном районе может быть определена на основании теоремы Байеса:
| (34) |
где W(0) плотность (безусловная) распределения направлений движения объекта при маневре из точки R0; Ф область определения W(0).
При отсутствии у разведчика сведений о возможных направлениях движения 0, область Ф растягивается в интервал длиной 2p, а плотность распределения направлений обращается в
W(0)=![]() .
.
Используя в (34) W(DR,t|0) из (33), можно получить
| (35) |
где приняты те же обозначения, что и в (34). Поскольку положение интервала Ф, которому должна принадлежать W(0) в достаточной мере произвольно, в (35) считается, что 0[-p-;p-).
Входящий в (35) интеграл может быть преобразован к виду
| (36) |
где обозначено ![]() и учтено, что
и учтено, что ![]() четная функция . Используя интегральное представление модифицированной функции Бесселя мнимого аргумента Iv(z):
четная функция . Используя интегральное представление модифицированной функции Бесселя мнимого аргумента Iv(z):
| (37) |
и учитывая, что ![]() , можно переписать соотношение (38) в форме
, можно переписать соотношение (38) в форме
| (39) |
Тогда окончательно из (34) следует, что
| (40) |
Полученная плотность распределения вероятностей не зависит от ![]() . В любом сечении W(DR,t) плоскостью, нормальной к плоскости маневрирования в позиционном районе {RxDyD} и проходящей через точку xD=yD=0, распределение представляется одинаковыми кривыми закона Райса. В пространстве над плоскостью {RxDyD} этой плотности соответствует поверхность, изображенная на рис.3.
. В любом сечении W(DR,t) плоскостью, нормальной к плоскости маневрирования в позиционном районе {RxDyD} и проходящей через точку xD=yD=0, распределение представляется одинаковыми кривыми закона Райса. В пространстве над плоскостью {RxDyD} этой плотности соответствует поверхность, изображенная на рис.3.

Рис.3. Априорная плотность при перемещении объекта разведки по неизвестному
направлению в районе маневрирования
При малых значениях времени, когда ![]() , плотность распределения вероятностей мгновенного положения объекта представляется поверхностью, которую опишет кривая закона Релея, если ее вращать вокруг оси, совпадающей с R0. По мере увеличения продолжительности интервала времени, прошедшего с момента t=0, начала маневра перемещения из точки проведения сеанса излучения сигнала, сечение кривой плотности распределения "расплывается" и форма кривой в сечении приближается к гауссовой. Таким образом, плотность распределения вероятностей мгновенного положения объекта разведки при его маневре в пространстве ведет себя во времени как затухающая волна, которая распространяется из точки начального положения R0, где объект излучал сигнал и мог быть обнаружен и идентифицирован, во все стороны скоростью
, плотность распределения вероятностей мгновенного положения объекта представляется поверхностью, которую опишет кривая закона Релея, если ее вращать вокруг оси, совпадающей с R0. По мере увеличения продолжительности интервала времени, прошедшего с момента t=0, начала маневра перемещения из точки проведения сеанса излучения сигнала, сечение кривой плотности распределения "расплывается" и форма кривой в сечении приближается к гауссовой. Таким образом, плотность распределения вероятностей мгновенного положения объекта разведки при его маневре в пространстве ведет себя во времени как затухающая волна, которая распространяется из точки начального положения R0, где объект излучал сигнал и мог быть обнаружен и идентифицирован, во все стороны скоростью ![]() . Задаваясь требованиями на априорную для разведчика плотность распределения вероятностей мгновенного положения объекта разведки к началу каждого следующего сеанса излучения сигнала, можно на основе полученных соотношений определить требуемое время радиомолчания tп, т. е. длительность паузы между сеансами излучения.
. Задаваясь требованиями на априорную для разведчика плотность распределения вероятностей мгновенного положения объекта разведки к началу каждого следующего сеанса излучения сигнала, можно на основе полученных соотношений определить требуемое время радиомолчания tп, т. е. длительность паузы между сеансами излучения.
Так, например, для объектов установленных на автомобиле, движущихся в процессе маневрирования в со средней скоростью порядка ![]() и с дисперсией
и с дисперсией ![]() (такое значение соответствует случайному равновероятному изменению мгновенной скорости движения в пределах [0,2<V>]), из (40), следует, что в окрестности максимального значения плотности W(DR,t) условной вероятности нахождения объекта разведки в пределах площадки размером S=1км´1км спустя время t после начала маневра смены позиции будет
(такое значение соответствует случайному равновероятному изменению мгновенной скорости движения в пределах [0,2<V>]), из (40), следует, что в окрестности максимального значения плотности W(DR,t) условной вероятности нахождения объекта разведки в пределах площадки размером S=1км´1км спустя время t после начала маневра смены позиции будет
| (41) |
Безусловная априорная вероятность обнаружения мобильного объекта разведки равна произведению
Р=Р1Р(1|1) | (42) |
условной вероятности P1 обнаружения и идентификации объекта во время предыдущего сеанса работы на излучение на вероятность P(1|1).
При движении маневрирующего объекта по железной дороге условная априорная вероятность нахождения его в окрестности точки DR тоже может быть определена согласно (42). Если при этом принять <V> 60 км/ч (пассажирская скорость), а ![]() в окрестности максимума плотности условной вероятности мгновенного положения будет
в окрестности максимума плотности условной вероятности мгновенного положения будет
| (43) |
где k число ветвлений возможного пути за время движения между сеансами работы на излучение.
Список литературы
1. Куприянов А.И., Шустов Л.Н. Радиоэлектронная борьба. Основы теории. М.: Вузовская книга, 2011. 798 c.
2. Оуэн Г. Теория игр.– М.:"Мир", 1971. 230 с.
3. Маделунг Э. Математический аппарат физики. М.:Наука, 1962. 618 c.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||