научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
УДК 004.93'12
МГТУ им. Н.Э. Баумана
Введение
Распознавание древнерусской скоропись XVII в. (рис. 1) представляет собой сложную задачу. По сравнению с машинопечатным текстом, в данном виде текста отсутствует большинство закономерностей, позволяющих делать весомые допущения в процессе распознавания. Так, в скорописи отсутствуют чёткие промежутки между буквами и словами, не прослеживается точное соответствие в начертании одинаковых символов (вариативность начертания), возможны всевозможные дефекты начертаний и случайные пересечения штрихов символов.

Рисунок 1 - Фрагмент древнерусского скорописного текста XVII в.
В работе [3], посвящённой разработке технологии электронного издания скорописных документов XVII в., был предложен метод автоматического выделения прямоугольных областей слов в изображениях скорописного текста. Однако задача распознавания в этой работе не рассматривалась. В работах [1,2] предложена методика распознавания данных текстов. Она основывается на структурном подходе к распознаванию и организации процесса распознавания в виде дисциплины выдвижения и проверки гипотез с использованием экспертных знаний. Процесс распознавания текста представляется в данном методе в виде процесса решения серии вложенных подзадач — распознавания всех слов текста и распознавания всех букв каждого из слов. Система распознавания, организованная подобным образом, предполагает наличие в своей структуры базы знаний (БЗ), хранящей структурные описания букв распознаваемого алфавита и слов, составляющих словник системы.
Данная работа посвящена подходу к распознаванию абстрактных образов, лежащего в основе используемых предложенной методикой алгоритмов распознавания букв и слов скорописи. Рассматривается общий принцип построения структурных фреймовых описаний объектов распознавания в БЗ системы распознавания и подход к распознаванию образов путём выдвижения и проверки гипотез, адаптированный к вводимым структурным описаниям образов. Предлагается способ фреймового представления гипотез, выдвигаемых системой относительно распознаваемого образа на основе имеющихся структурных описаний. Приводится описание и обоснование абстрактного алгоритма распознавания. Исследование данного подхода в применении к распознаванию букв и слов скорописи будет описано в последующей работе.
1. Фреймовая сеть структурных описаний
В данном разделе описывается структура фреймовой сети БЗ: типы составляющих её узлов и возможные отношения между ними. Для описания типов и отношений узлов БЗ используется нотация дескриптивной логики [4], а для отражения логических свойств наборов узлов используется теоретико-множественный аппарат.
Все узлы, составляющие фреймовую сеть, считаются объектами общего типа Узел. В зависимости от вида представляемых объектов, конкретные узлы будут иметь один из вводимых ниже типов, являющихся подтипами типа Узел, т.е. для каждого объекта a в фреймовой сети верно утверждение Узел(a).
Для структурного описания абстрактного объекта распознавания вводится тип узлов ДетализируемыйУзел. Данный тип узлов является общим для всех фреймов, обозначающих сложные в структурном смысле объекты. Т.е. узлы данного типа обозначают те объекты, для описания структуры которых служат прочие узлы фреймовой сети.
ДетализируемыйУзел ⊑ Узел.
Описание детализируемого объекта строится из перечисления видов составляющих его элементов и их взаимоотношений. Причём, с одной стороны, объект может иметь несколько вхождений элементов одного вида, с другой стороны, различные объекты могут иметь одинаковые элементы. Для отражения данного обстоятельства понятия элемента объекта и его вхождения в структуру объекта разделяются. Описание объекта состоит из набора вхождений различных элементов. Понятие вхождения отражает единичный факт присутствия в объекте того или иного элемента. Если, к примеру, буква содержит две вертикальные линии, это может быть описано двумя экземплярами “вхождения”, ссылающимися на один экземпляр элемента “вертикальная линия”. Таким образом, элементы являются общими для всех объектов, а их вхождения – уникальными.
Набор отношений между разделяемыми видами элементов всегда индивидуален для каждого объекта, следовательно. под отношениями элементов объекта подразумеваются отношения между вхождениями элементов, а не между самими элементами.
Таким образом, описание ДетализируемогоУзла состоит из набора узлов типа ВхождениеЭлемента и ВхождениеОтношения, являющихся подтипами типа ВхождениеСвойства. Факт детализации ДетализируемогоУзла d узлом ВхожденияСвойства q (т.е. вхождением элемента или отношения) обозначается как детализирует(q,d). Каждый узел ВхожденияЭлемента связан с единственным узлом типа Элемент. Будем говорить, что ВхождениеЭлемента q индицирует наличие данного Элемента e в объекте, и будем обозначать это как индицирует(q,e). Таким образом:
Элемент ⊑ Узел;
ВхождениеСвойства ≡ Узел ⊓ (=1 детализирует.ДетализируемыйУзел);
ВхождениеЭлемента ≡ ВхождениеСвойства ⊓
⊓ (= 1 индицирует.Элемент).
Любое отношение элементов можно представить в виде кортежа связанных этим отношением элементов. Узлы типа ВхождениеОтношения должны иметь несколько именованных слотов для ссылки на ВхожденияЭлементов, участвующие в данном экземпляре отношения. Для всех видов связей по этим слотам используется общее название — включение вхождений элементов.
ВхождениеОтношения ≡ ВхождениеСвойства ⊓
⊓ (≥ 1 включаетВхождение.ВхождениеЭлемента).
Некоторые сложные в структурном смысле объекты, описываемые фреймами типа ДетализируемыйУзел, сами могут являться элементами более крупных объектов. Так, например, буква в тексте является частью слова. Кроме того, один и тот же элемент, входящий в структуру сложного образа, может иметь несколько принципиально различных представлений, которые, однако, не влияют на его роль в структуре объемлющего образа. Буква может иметь несколько способов начертания, и в составе изображений слов может встречаться любое из них: все способы начертания данной буквы служат для обозначения этой буквы в составе слова.
Введём следующие отношения между ДетализируемымиУзлами и Элементами, позволяющие учитывать эти возможные явления. Если элемент какого-либо образа имеет сложную структуру, то соответствующий фрейм-Элемент в БЗ должен иметь ссылку на ДетализируемыйУзел, описывающий данную структуру. Соответственно, если элемент может иметь несколько различных сложных представлений, то таких ссылок должно быть несколько, по числу представлений:
Элемент ⊑ Узел ⊓ (∀имеетОписание.ДетализируемыйУзел).
Таким образом, ДетализируемыеУзлы описывают структурные взаимоотношения Элементов низшего уровня в составе Элемента высшего уровня. Несколько ДетализируемыхУзлов могут описывать структуру одного и того же Элемента. Связь, обратная связи имеетОписание, отражает смысл, который данный ДетализируемыйУзел имеет в структуре более сложных ДетализируемыхУзлов.
На данном этапе базу знаний можно представить как
Б = (D, E, F) = (D, E, Q ∪ R) ,
где D = {d ∣ ДетализируемыйУзел(d)} – множество детализируемых узлов;
E = {e ∣ Элемент(e)} – множество элементов;
F = {f ∣ ВхождениеСвойства(q)} – множество вхождений свойств;
Q = {q ∣ ВхождениеЭлемента(q)} ⊆ F– множество вхождений элементов;
R = {r ∣ ВхождениеОтношения(r)} ⊆ F – множество вхождений отношений.
Далее ДетализируемыеУзлы, входящие в множество D, будут называться фреймами-образами, просто образами или объектами распознавания.
На рисунке 2 проиллюстрирован общий принцип построения структурных описаний объектов распознавания с помощью Элементов и ВхожденийСвойств.

Рисунок 2 - Общая структура базы знаний
Для обозначения узлов-ВхожденийСвойств, описывающих структуру отдельно взятого фрейма d ∈ D, вводится обозначение q(d), которое равносильно утверждению
ВхождениеСвойства(q) ∧ детализирует(q, d).
Множество узлов-вхождений в детализируемом узле будет записываться как F(d) = {f(d)}. При помощи таких обозначений набор узлов, составляющих описание одного объекта, может быть представлен в виде
(d∈ D, F(d) ⊆ F) = (d, Q(d) ⊆ Q ∪ R(d) ⊆ R).
Для обозначения множества узлов-вхождений, индицирующих узлы определённого типа T, будет использоваться обозначение FT(d).
2. Виртуальный фрейм
Процесс распознавания образа в принятом методе заключается в попытке согласовании наблюдаемого фрагмента изображения с одним из фреймов в базе знаний. Образ считается найденным и распознанным, если удалось увязать составляющие его элементы с элементами, входящими в описание одного из фреймов. В этом случае можно говорить, что найден образ, соответствующий согласующемуся фрейму.
В процессе распознавания образа для сохранения получаемой информации об изображении в динамической памяти системы строится фреймовая модель, описывающая наблюдаемую в каждый текущий момент картину — виртуальный фрейм (ВФ). Он строится по тем же правилам, что и фреймы распознаваемых объектов в БЗ, но существует только во время текущей сессии распознавания.
Процесс распознавания образа строится на цикле обращений к модулю распознавания структурных элементов. В случае распознавания букв таким модулем является трассировщик изображения, выделяющий на изображении отдельные линии в буквах. Каждый успешный вызов распознавателя элементов даёт очередную порцию информации о структуре изображения, а именно — обнаруженный элемент образа. О найденном элементе известно, каковы значения определённых его характеристик и каковы его взаимоотношения с прочими найденными элементами. На основе этого в ВФ можно добавить узел, обозначающий вхождение найденного элемента в распознаваемый образ, и связать его отношением индикации с узлом-Элементом в БЗ, обозначающим данный тип элементов. Необходимо также отразить отношения между элементом, добавляем в ВФ, и прочими элементами в виде ВхожденийОтношений.
Итак, виртуальный фрейм является динамическим расширением базы знаний:
![]() ,
,
где ![]() – узел, обозначающий виртуальный фрейм и имеющий тип
– узел, обозначающий виртуальный фрейм и имеющий тип
распознаваемого объекта;
Q(![]() )⊂Q = {q(
)⊂Q = {q(![]() ) | ВхождениеЕлемента(q(
) | ВхождениеЕлемента(q(![]() )) ∧
)) ∧
∧ ∃e∈E индицирует(q(![]() ), e)},
), e)},
R(![]() ) ⊂ R = {r(
) ⊂ R = {r(![]() ) | ВхождениеОтношения(r(
) | ВхождениеОтношения(r(![]() )) ∧
)) ∧
∧ (∀ q включаетВхождение(r(![]() ), q) ⇒ q ∈ Q(
), q) ⇒ q ∈ Q(![]() ) ) }.
) ) }.
Пусть в результате первого обращения к распознавателю элементов обнаружен элемент некоторого типа x∈E, и в ВФ построено его описание q(![]() )∈Q(
)∈Q(![]() ). Можно выдвинуть первые гипотезы, предположив, что наблюдается один из образов, содержащих в своей структуре элемент найденного типа. Кандидатами становятся ДетализируемыеУзлы, которые содержат хотя бы один узел ВхожденияЭлемента, индицирующего элемент данного типа. Множество этих фреймов можно выразить как
). Можно выдвинуть первые гипотезы, предположив, что наблюдается один из образов, содержащих в своей структуре элемент найденного типа. Кандидатами становятся ДетализируемыеУзлы, которые содержат хотя бы один узел ВхожденияЭлемента, индицирующего элемент данного типа. Множество этих фреймов можно выразить как
где x∈E — найденный Элемент, индицируемый построенным узлом q(![]() )∈Q(
)∈Q(![]() ) виртуального фрейма.
) виртуального фрейма.
Таким образом, признаком потенциальной пригодности фрейма для описания частично рассмотренного образа является наличие в нём узла ВхожденияЭлемента, индицирующего тот же Элемент, что и построенный узел в ВФ. Иллюстрация такой ситуации приведена на рисунке 3а. Между этим узлом и построенным узлом ВФ можно установить некое отношение соответствия, которое будет назваться отношением согласования. Аналогичное отношение можно установить между узлами ВхожденийОтношений ВФ и фрейма БЗ. Будем записывать установленное отношение данного типа как согласован(f(d), f(![]() )).
)).

Рисунок 3 – Виртуальный фрейм и его согласование с фреймами БЗ
(а – по одному узлу в ВФ; б – по нескольким узлам в ВФ)
Условие установления отношения согласования между узлами ВхожденийЭлементов записывается как:
согласован (q(d), q(![]() )) ⇒ ∃x∈E (индицирует (q(d), x) ∧
)) ⇒ ∃x∈E (индицирует (q(d), x) ∧
∧ индицирует (q(![]() ),x)),
),x)),
где q(d) ∈ Q(d), q(![]() ) ∈ Q(
) ∈ Q(![]() ).
).
Аналогичное условие для ВхожденийОтношений:
согласован (r(d), r(![]() )) ⇒ (∀q(
)) ⇒ (∀q(![]() ) ∈ Q(
) ∈ Q(![]() ), включаетВхождение (r(
), включаетВхождение (r(![]() ), q(
), q(![]() )))
)))
(согласован(q(d), q(![]() )) ∧ включаетВхождение (r(d), q(d)) ),
)) ∧ включаетВхождение (r(d), q(d)) ),
где r(d) ∈ R(d), r(![]() ) ∈ R(
) ∈ R(![]() ).
).
Тогда выражение (1) можно переписать в виде
{d∈ D | ∃ q(d) ∈ Q(d) согласован(q(d), q(![]() )) }.
)) }.
Теперь предположим, что на некотором этапе ВФ содержит вхождения более чем одного элемента, связанные некоторыми установленными отношениями. Тогда список фреймов-кандидатов ограничивается множеством фреймов-образов, согласующихся с каждым из найденных элементов (см. рис. 3б):
причём каждый из элементов f(![]() ) и f(d) может состоять только в одном отношении согласования. На самом деле, действие квантора всеобщности в выражении (2) слишком строгое. Далее в разделах 4 и 5 будет пояснено, что согласовываться могут не все узлы ВФ, но это оказывает влияние на правдоподобность гипотез.
) и f(d) может состоять только в одном отношении согласования. На самом деле, действие квантора всеобщности в выражении (2) слишком строгое. Далее в разделах 4 и 5 будет пояснено, что согласовываться могут не все узлы ВФ, но это оказывает влияние на правдоподобность гипотез.
Выше было отмечено, что в состав образа могут входить несколько элементов одного типа. Тогда вхождение этого элемента в ВФ может быть согласовано с каждым из имеющихся его вхождений в фрейме-образе в БЗ. В таком случае следует выдвинуть несколько гипотез, каждая из которых указывает на один и тот же образ, но предполагает разные схемы согласования фактической информации с данным фреймом БЗ.
В следующем разделе вводится способ фреймового описания выдвигаемых гипотез.
3. Гипотезы
Определим понятие гипотезы как соответствие между одним из фреймов-образов в БЗ и схемой его согласования с ВФ. Для представления выдвигаемых гипотез в динамической памяти системы строятся специальные фреймовые структуры, корневыми узлами которых являются узлы типа Гипотеза. Каждый такой узел ссылается на предполагаемый гипотезой фрейм-образ в БЗ и содержит набор ссылок на узлы типа Согласование. Узлы последнего типа содержат в своих слотах ссылки на пары согласуемых данной гипотезой узлов в фрейме БЗ и ВФ.
Гипотеза ≡ Узел ⊓ (= 1 предполагает.ДетализируемыйУзел) ⊓
⊓ (∀содержит.Согласование),
Согласование ≡ Узел ⊓ (= 1 узелБЗ.ВхождениеСвойства) ⊓
⊓ (= 1 узелВФ.ВхождениеСвойства).
Таким образом, под гипотезой следует понимать пару
(h, S(h))
где Гипотеза (h) – узел, обозначающий данную гипотезу;
d∈D : предполагает (h, d) – фрейм-образ в БЗ, предполагаемый данной гипотезой;
S(h) { s| Согласование(s) ∧ содержит(h, s) ∧
∧ (∃! (f(d), f(![]() )) (узелБЗ(s, f(d)) ∧ узелВФ(s, f(
)) (узелБЗ(s, f(d)) ∧ узелВФ(s, f(![]() )) ) } – множество пар,
)) ) } – множество пар,
задающих схему согласования узлов-Вхождений из ВФ (не обязательно
всех) и предполагаемого фрейма-образа.
Множество S(h) называется схемой гипотезы h.
На рисунке 4 показаны примеры представления гипотез. На рисунке 4а показаны две гипотезы, содержащие по одному узлу-согласованию и согласующие ВФ с разными фреймами-образами в БЗ. На рисунке 4б две аналогичные гипотезы указывают различные схемы согласования ВФ с одним и тем же фреймом-образом.

Рисунок 4 – Представление двух гипотез и их схем согласования ВФ
(а – разными фреймами; б – с одним фреймом)
Узлы типа Согласование служат для отражения устанавливаемых отношений согласования. Причём, как следует из введённого определения гипотезы, отношение согласования устанавливается в рамках конкретной гипотезы, поэтому при указания согласованности узлов может указываться соответствующая гипотеза. Если гипотеза не указывается, то имеется ввиду согласование в рамках хотя бы одной из имеющихся гипотез.
согласован(f(d), f(![]() ), h) ⇔ ∃z : Согласование(z) ∧ содержит(h, z) ∧
), h) ⇔ ∃z : Согласование(z) ∧ содержит(h, z) ∧
∧ узелБЗ (z,f(d)) ∧ узелВФ (z,f(![]() )).
)).
Любой из узлов фрейма БЗ и ВФ в рамках одной гипотезы может участвовать только в одном согласовании:
| согласован (f(d),f1( согласован (f1(d),f( |
Далее будут использоваться т.н. проекции схем согласования гипотез на БЗ и на ВФ для отражения наборов узлов БЗ и ВФ соответственно, согласуемых данной гипотезой. Эти множества обозначаются и определяются как:
где T– некоторый произвольный тип узлов.
Набор гипотез, выдвигаемых при обнаружении единственного структурного элемента и предполагающих образы из множества (1), строится в соответствии с принципом (5). В нём учитывается возможность выдвижения нескольких гипотез относительно одного образа. Пусть найден единственный элемент x∈E, индицированный в ВФ узлом q(![]() ). Тогда первоначальный набор гипотез будет задаваться как
). Тогда первоначальный набор гипотез будет задаваться как
Лемма 1. В любой гипотезе h (предполагает(h, d), d∈D) для каждого типа узлов T выполняется STБЗ(h) ⊆ FT(d) и STВФ(h) ⊆ FT(![]() ).
).
Доказательство. Следует из определения (4) и того факта, что по правилу (3) отношение согласования в рамках одной гипотезы является взаимнооднозначным.
∎
Следствие. Для любой гипотезы h (предполагает(h,d), d∈D) выполняется |S(h)| = |F(d)| ⇔ SБЗ(h) = F(d) и |S(h)| = |F(![]() )| ⇔ SВФ(h) = F(
)| ⇔ SВФ(h) = F(![]() ).
).
Доказательство.
Необходимость. Следует из леммы 1 и тех фактов, что
 ,
,  и
и  .
.
Достаточность. Очевидна для обоих утверждений.
∎
4. Характеристики гипотез
Определение 1. Функцией веса набора узлов-Вхождений F(d) называется любая функция w : F(d) → ℝ, обладающая следующими свойствами:
1. ∀ F(d) w(F(d)) ≥ 0;
2. F(d1) ⊆ F(d2) ⇒ w(F(d1)) ≤ w(F(d2));
3. F(d1) = F(d2) ⇒ w(F(d1)) = w(F(d2)).
Определение 2. Функцией веса гипотезы hназывается любая функция w : h → ℝ, обладающая следующими свойствами:
1. ∀h w(h) ≥ 0;
2. S(h1) ⊆ S(h2) ⇒ w(h1) ≤ w(h2);
3. S(h1) = S(h2) ⇒ w(h1) = w(h2);
4. ∀h w(h) = w(SБЗ(h)) = w(SВФ(h)).
Лемма 2. Для любой гипотезы h (предполагает(h,d), d∈D) выполняется w(h) ≤ w(F(d)) и w(h) ≤ w(F(![]() )).
)).
Доказательство. Верность обоих неравенств следует из свойств 2 функций веса (определения 1 и 2) и леммы 1.
∎
Лемма 3. Для любой гипотезы h (предполагает(h,d), d∈D) выполняется |S(h)| = |F(d)| ⇒ w(h) = w(F(d)) и |S(h)| = |F(![]() )| ⇒ w(h) = w(F(
)| ⇒ w(h) = w(F(![]() )).
)).
Доказательство. По следствию леммы 1, условие |S(h)| = |F(d)| влечёт за собой утверждение SБЗ(h) = F(d). Отсюда по свойству 3 определения 1 следует, что w(SБЗ(h)) = w(F(d)). По свойству 4 определения 2 это можно переписать в виде w(h) = w(F(d)), что и требовалось доказать. Доказательство для ![]() аналогично.
аналогично.
∎
Рассмотрим произвольную гипотезу h (предполагает(h,d), d∈D). Степенью согласованности гипотезы назовём величину
а степенью пригодности гипотезы – величину
Введём понятие степени проверенности гипотезы для отражения прогресса её проверки в процессе распознавания. Для этого расширим понятие гипотезы, добавив третий компонент в её определение:
(h, S(h), Qпров(h)),
здесь Qпров(h)⊆Q(d) – множество узлов-ВхожденийЭлементов в фрейме-образе, указываемом данной гипотезой, для которых была выполнена попытка отыскания на изображении соответствующих фрагментов, успешно или нет.
В зависимости от специфики конкретного алгоритма распознавания, учёт проверенности может выполняться не для всех типов элементов, входящих в структуры образов, а только для определённого набора типов, наиболее значимых для распознавания образа. Т.е. конкретный алгоритм распознавания может осуществлять целенаправленную проверку элементов лишь некоторых типов, обрабатывая присутствие элементов остальных типов попутно.
Для отражения подобных особенностей введём весовую функцию проверенности wП над множествами вхождений элементов Q(d). Она совершенно аналогична по свойствам весовой функции, введённой в определении 1, но распределяет веса узлов по их типам так, что на её значение влияет присутствие в Q(d) узлов только «важных» для распознавания типов.
Тогда степенью проверенности гипотезы будет называться величина

Введём также правило, по которому узел фрейма БЗ, участвующий в одном из согласований гипотезы h, автоматически включается в список проверенных узлов Qпров(h):
Назовём степенью успешности гипотезы величину, отражающую отношение числа согласованных ВхожденийЭлементов к числу проверенных вхождений:
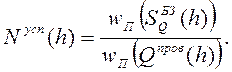
Рассмотрим некоторые свойства введённых характеристик.
Свойство 1. Область значений степени согласованности равна [0, 1].
Доказательство. Рассмотрим произвольную гипотезу h (предполагает(h,d), d∈D). Т.к. число узлов в фрейме БЗ d постоянно, то в определении (6) |F(d)| = const > 0 и w(F(d)) = const > 0 (фреймы с пустым множеством вхождений не рассматриваются). Следовательно, область значений Nсогл определяется величиной w(h).
По свойству 1 определения 2: 0 ≤ w(h) , а по лемме 2: w(h) ≤ w(F(d)), откуда вытекает:
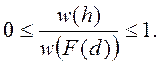
∎
Свойство 2. При добавлении узлов в ВФ степень согласованности гипотезы не убывает.
Доказательство. При отсутствии узлов в ВФ гипотеза не может содержать ни одного согласования. Следовательно, в этом случае w(h) = 0 и Nсогл = 0.
∎
Пусть в определённый момент в ВФ содержится некоторое количество узлов и в рамках гипотезы h установлено nk = |S(h)| согласований с общим весом wk(h). Новый узел, добавляемый в ВФ, в рамках h может быть либо согласован с одним из узлов фрейма d, либо не согласован ни с одним из узлов. В первом случае новое число согласований увеличится на 1: nk+1 = nk + 1, и соответственно будет выполняться wk+1(h) ≥ wk(h); во втором случае число согласований не изменится: nk+1 = nk и wk+1(h) = wk(h). Поскольку при добавлении узла в ВФ число узлов в фрейме d не меняется (w(F(d)) = const), то при любом результате согласования нового узла в соответствии с (6) будет выполняться

∎
Свойство 3. Область значений степени пригодности равна [0, 1].
Доказательство. По определению (7), при отсутствии в ВФ узлов-вхождений степень пригодности принимает значение 1. По лемме 2 значение w(h) лежит в интервале [0, w(F(![]() ))]. Следовательно, выполняется
))]. Следовательно, выполняется

∎
Свойство 4. При добавлении в ВФ узлов, не согласуемых гипотезой с фреймом БЗ, степень пригодности гипотезы не возрастает.
Доказательство. При отсутствии узлов в ВФ имеем |F(![]() )| = 0, что по определению (7) влечёт Nприг = 1.
)| = 0, что по определению (7) влечёт Nприг = 1.
Пусть в определённый момент в ВФ содержится некоторое количество узлов mk = |F(![]() )| и в рамках гипотезы h установлено nk = |S(h)| согласований с общим весом wk(h). При добавлении в ВФ нового узла будет выполнено mk+1 = mk + 1 и wk+1(F(
)| и в рамках гипотезы h установлено nk = |S(h)| согласований с общим весом wk(h). При добавлении в ВФ нового узла будет выполнено mk+1 = mk + 1 и wk+1(F(![]() )) ≥ wk(F(
)) ≥ wk(F(![]() )). При этом, если данный узел не согласуется гипотезой с фреймом БЗ, то число согласований не меняется: nk+1 = nk и wk+1(h) = wk(h). Следовательно:
)). При этом, если данный узел не согласуется гипотезой с фреймом БЗ, то число согласований не меняется: nk+1 = nk и wk+1(h) = wk(h). Следовательно:

∎
Свойство 5. При добавлении в ВФ узлов, согласуемых гипотезой с фреймом БЗ, степень пригодности гипотезы не убывает.
Доказательство. Пусть в определённый момент в ВФ содержится некоторое количество узлов mk = |F(![]() )| и в рамках гипотезы h установлено nk = |S(h)| согласований с общим весом wk(h). При добавлении в ВФ нового узла будет выполнено mk+1 = mk + 1, а вес узлов ВФ увеличится на некоторую величину: wk+1(F(
)| и в рамках гипотезы h установлено nk = |S(h)| согласований с общим весом wk(h). При добавлении в ВФ нового узла будет выполнено mk+1 = mk + 1, а вес узлов ВФ увеличится на некоторую величину: wk+1(F(![]() )) = wk(F(
)) = wk(F(![]() )) + Δw, Δw ≥ 0. По условию данный узел согласуется гипотезой с фреймом БЗ, и число согласований увеличивается: nk+1 = nk + 1, что влечёт за собой увеличение веса гипотезы. Т.к. согласование, добавляемое в гипотезу, включает добавленный в ВФ узел, то вклад этого согласования в общий вес гипотезы будет равен вкладу добавленного узла в общий вес узлов ВФ. Таким образом, wk+1(h) = wk(h) + Δw. Учитывая, что Δw ≥ 0 и что по лемме 2 w(h) ≤ w(F(
)) + Δw, Δw ≥ 0. По условию данный узел согласуется гипотезой с фреймом БЗ, и число согласований увеличивается: nk+1 = nk + 1, что влечёт за собой увеличение веса гипотезы. Т.к. согласование, добавляемое в гипотезу, включает добавленный в ВФ узел, то вклад этого согласования в общий вес гипотезы будет равен вкладу добавленного узла в общий вес узлов ВФ. Таким образом, wk+1(h) = wk(h) + Δw. Учитывая, что Δw ≥ 0 и что по лемме 2 w(h) ≤ w(F(![]() )), получим:
)), получим:

∎
5. Распознавание
Характеристики гипотез, введённые в разделе 4, используются в процессе распознавания следующим образом. В каждый момент процесса распознавания система располагает списком выдвинутых гипотез H = {h : Гипотеза(h)}. Гипотеза h∈H считается полностью проверенной, если выполняется условие проверенности:
| Упров(h) ⇔ Nпров(h) = 1. |
|
Гипотеза h называется согласованной, если степень её согласованности превышает порог согласованности Псогл. Это условие согласованности можно записать как:
| Усогл(h) ⇔ Nсогл(h) ≥ Псогл. |
|
Гипотеза h∈H считается пригодной для дальнейшего рассмотрения, если степень её пригодности имеет значение не ниже порога пригодности Пприг. В противном случае она считается несостоятельной. Это условие называется условием пригодности и записывается в виде:
| Уприг(h) ⇔ Nприг(h) ≥ Пприг. |
|
Опровергнутой называется гипотеза, в которой достаточная часть проверенных элементов не была согласована, т.е. согласование которой в достаточной мере неуспешно. Подобные гипотезы будут удовлетворять условию опровержения:
| Уопр(h) ⇔ Nусп(h) < Пусп. |
|
Пригодные и неопровергнутые гипотезы будут называться вполне пригодными, и отвечать полному условию пригодности:
Согласованная гипотеза считается подтверждённой, если она пригодна и полностью проверена, что назовём условием подтверждённости:
Наконец, гипотеза h считается наиболее правдоподобной, если выполняется условие
Алгоритм распознавания образов, основанный на приведённом способе структурного описания и управляемый выдвижением и проверкой гипотез, в общем виде без учёта особенностей конкретной предметной области можно представить следующим образом:
Алгоритм 1. Распознавание абстрактных образов.
Начало
1. Найти на изображении элемент известного вида.
2. Выдвинуть первоначальный список гипотез в соответствии с правилом (5).
3. Цикл:
4. Вычислить характеристики всех имеющихся гипотез.
5. Удалить гипотезы, нарушившие полное условие пригодности Уп.приг (9).
6. Если не осталось гипотез:
7. Вернуть ошибку.
8. Конец алгоритма
9. Если есть подтверждённые по Уподтв (10) гипотезы и выполняется
∄h∈H : Уп.приг(h) ∧ ![]() .
.
10. Вернуть подтверждённую гипотезу с максимальной Nсогл.
11. Конец алгоритма
12. Выбрать рабочую гипотезу h по правилу (11).
13. Выбрать в фрейме БЗ d (предполагает(h,d)) вхождение элемента q
из множества Q(d) \ Qпров(h).
14. Выполнить Qпров(h) ← Qпров(h) ∪ q.
15. Вызвать модуль распознавания элементов для поиска элемента,
описываемого узлом q.
16. Если элемент найден:
17. Поместить фактическую информацию о найденном элементе в ВФ.
18. Согласовать новые узлы ВФ во всех гипотезах с учётом правила (8).
19. При необходимости выдвинуть новые гипотезы.
20. Конец цикла.
Конец алгоритма
На шаге 2 строится список гипотез H = H0, отвечающих единственному найденному на шаге 1 элементу x. В соответствии с правилом (5) в этот список помещается по одной гипотезе на каждое вхождение элемента найденного типа в любой фрейм-образ в БЗ. Соответственно, количество первоначальных гипотез вычисляется как |H0| = |{q∈Q : индицирует(q,x)}|. Суть алгоритма заключается в проверке всех выдвинутых гипотез путём отыскания на изображении подразумеваемых ими структурных элементов. При этом характеристики гипотез позволяют по мере выполнения проверок, во-первых, отбрасывать неперспективные гипотезы, а во-вторых, стремиться к приоритетной проверке наиболее правдоподобных гипотез.
Алгоритм стремится учитывать все возможные схемы согласования поступающей информации с фреймами БЗ. Это порождает необходимость в некоторых случаях при обнаружении на изображении очередного элемента выдвигать дополнительные гипотезы. Например, на итерации k среди прочих имеется гипотеза h∈H со схемой согласования Sk(h) и предполагаемым образом d∈D. Пусть на итерации k+1 найден элемент некоторого типа x и в ВФ добавлен соответствующий узел-вхождение q(![]() ) : индицирует(q(
) : индицирует(q(![]() ),x)). Фрейм d в множестве вхождений Q(d) \ Qпров(h) может не содержать вхождения элемента типа x, может содержать одно такое вхождение, а может содержать и несколько. Пусть в последнем случае такими вхождениями являются узлы qi(d) (i=1…n) : индицирует(qi(d), x)). В этом случае гипотеза h «расщепляется» на n гипотез hi, для каждой из которых выполняется предполагает(hi, d), Sk+1(hi) = Sk(hi) ∪ si, где узелВФ(si, q(
),x)). Фрейм d в множестве вхождений Q(d) \ Qпров(h) может не содержать вхождения элемента типа x, может содержать одно такое вхождение, а может содержать и несколько. Пусть в последнем случае такими вхождениями являются узлы qi(d) (i=1…n) : индицирует(qi(d), x)). В этом случае гипотеза h «расщепляется» на n гипотез hi, для каждой из которых выполняется предполагает(hi, d), Sk+1(hi) = Sk(hi) ∪ si, где узелВФ(si, q(![]() )), узелБЗ(si, qi(d)). При этом для каждой из новых гипотез множество проверенных узлов изменяется индивидуально: Qпров(hi) = Qпров(h) ∪ qi(d). В последующем каждая из n «расщеплённых» гипотез по тем же правилам может быть преобразована в n-1 дополнительных гипотез и т.д. В итоге гипотеза, содержащая n вхождений элементов x, может быть преобразована в n! альтернативных гипотез. Если считать, что в среднем образ содержит
)), узелБЗ(si, qi(d)). При этом для каждой из новых гипотез множество проверенных узлов изменяется индивидуально: Qпров(hi) = Qпров(h) ∪ qi(d). В последующем каждая из n «расщеплённых» гипотез по тем же правилам может быть преобразована в n-1 дополнительных гипотез и т.д. В итоге гипотеза, содержащая n вхождений элементов x, может быть преобразована в n! альтернативных гипотез. Если считать, что в среднем образ содержит ![]() различных элементов, каждый из которых входит в структуру образов в среднем
различных элементов, каждый из которых входит в структуру образов в среднем ![]() раз, то общее число альтернативных гипотез, которые могут быть выдвинуты относительно данного образа, т.е. общее число возможных согласований данного фрейма-образа с ВФ, равно
раз, то общее число альтернативных гипотез, которые могут быть выдвинуты относительно данного образа, т.е. общее число возможных согласований данного фрейма-образа с ВФ, равно
|
|
|
Утверждение 5.1. Алгоритм завершается за конечное число шагов.
Доказательство. На каждой итерации kцикла 3 выполняется проверка одного узла одной из гипотез. При этом список гипотез может сокращаться в связи с действием шага 5 или увеличиваться на шаге 19. Каждая гипотеза из H0 может быть преобразована в несколько альтернативных гипотез, вплоть до количества ![]() . Общее число гипотез может возрастать до среднего максимального значения
. Общее число гипотез может возрастать до среднего максимального значения ![]() . Тогда максимальное число узлов, которые необходимо проверить алгоритмом распознавания, можно выразить как
. Тогда максимальное число узлов, которые необходимо проверить алгоритмом распознавания, можно выразить как
![]()
где ![]() – среднее общее число элементов в образе (с повторениями).
– среднее общее число элементов в образе (с повторениями).
Достигнув этого максимального значения, число необходимых проверок на каждой итерации цикла будет убывать: на 1 за итерацию, если гипотезы не удаляются, или на 1 плюс число непроверенных узлов удалённых гипотез, если срабатывает шаг 5. Число оставшихся необходимых проверок напрямую влияет на степени проверенности и успешности гипотез, а они в свою очередь используются в условиях Уп.приг и Уподтв. Если для данной гипотезы выполнены все проверки, то она обязана быть признана либо подтверждённой на шаге 9, либо быть отвергнутой на шаге 5 (возможно даже ранее полной проверки). Следовательно, если выполнено в худшем случае ![]() проверок, то алгоритм будет завершён либо на шаге 8, либо на шаге 11.
проверок, то алгоритм будет завершён либо на шаге 8, либо на шаге 11.
∎
Утверждение 5.2. Если алгоритм завершается успешно, то в качестве ответа будет назван наблюдаемый образ.
Доказательство. Если на любой итерации цикла 3 в списке гипотез присутствует гипотеза h, предполагающая реально наблюдаемый образ, то эта гипотеза никогда не будет удалена на шаге 5. Покажем это.
Если на шаге 12 в качестве рабочей принимается гипотеза h1, отличная от h, то проверка очередного элемента в h1 либо заканчивается неудачей, что не снижает Nприг(h) и Nусп(h), либо приводит к добавлению в ВФ узла, согласующегося с h на шаге 16, что также не снижает полной пригодности h.
Пусть на какой-либо итерации на шаге 12 рабочей была принята гипотеза h. Проверка любого элемента h приводит к успешному его обнаружению и согласованию в h, т.к. по предположению h соответствует реально наблюдаемому образу. В соответствии со свойствами 2 и 5, это согласование увеличивает Nсогл(h) и, возможно, Nусп(h) и Nприг(h), что обеспечивает неснижение полной пригодности h.
Следовательно, гипотеза h, предполагающая наблюдаемый образ, всегда будет удовлетворять условию Уп.приг(h) и не будет удалена в процессе распознавания. Т.к. по условию алгоритм завершается успехом на шаге 11, эта гипотеза будет среди оставшихся в списке.
Покажем теперь, что при завершении алгоритма на шаге 11 будет выполнено Уподтв(h) и что Nсогл(h) будет максимальным среди удовлетворивших этому условию гипотез.
Условие на шаге 9 обеспечивает продолжение проверок гипотез до тех пор, пока есть хотя бы одна гипотеза h2, ещё не подтверждённая (![]() ), но всё ещё пригодная для рассмотрения (Уп.приг(h2)). Следовательно, рано или поздно гипотеза h будет проверена полностью, т.к. всегда удовлетворяет Уп.приг(h), как показано выше. А т.к. она по предположению соответствует реально наблюдаемому образу, то проверка её элементов (почти) всегда будет увеличивать степень её пригодности до удовлетворения условия Уподтв(h).
), но всё ещё пригодная для рассмотрения (Уп.приг(h2)). Следовательно, рано или поздно гипотеза h будет проверена полностью, т.к. всегда удовлетворяет Уп.приг(h), как показано выше. А т.к. она по предположению соответствует реально наблюдаемому образу, то проверка её элементов (почти) всегда будет увеличивать степень её пригодности до удовлетворения условия Уподтв(h).
Максимальность Nсогл(h) на шаге 11 обеспечивается следующим обстоятельством. Пусть на шаге 11 имеется какая-либо гипотеза h3, для которой выполнено Уп.приг(h3). Схема согласования этой гипотезы S(h3) отличается от схемы согласования S(h) по крайней мере одним согласованием (иначе гипотезы были бы идентичны). Т.к. только h соответствует наблюдаемому образу, различие в схемах согласования должно обеспечивать перевес степени согласованности Nсогл(h) по сравнению с Nсогл(h3). Т.е. элементы образов, в которых гипотезы расходятся между собой, должны лучше согласовываться в гипотезе h.
∎
Заключение
В статье рассмотрен способ структурного описания образов на основе фреймовых сетей. Описан способ организации процесса распознавания путём выдвижения и проверки гипотез с помощью механизма виртуального фрейма. Приведено описание алгоритма распознавания и показана его сходимость к правильному результату.
На основе описанного абстрактного подхода к распознаванию образов могут быть сформулированы конкретные методы распознавания букв и слов скорописи XVII в.. Для этого необходимо расширить предложенную схему построения базы знаний. Требуется ввести новые типы узлов, описывающие конкретные образы и составляющие их элементы. На основе введённых типов узлов необходимо задать конкретные весовые функции, используемые алгоритмом распознавания. Приведённый алгоритм распознавания абстрактных образов должен быть специфицирован для учёта конкретных особенностей конкретных предметных областей.
Список литературы
1. Зеленцов И.А. Выдвижение и проверка гипотез в системе распознавания древнерусской скорописи // Информационные технологии и письменное наследие: Материалы междунар. науч. конф. Уфа ‑ Ижевск, 2010. С. 99–101.
2. Зеленцов И.А. Метод распознавания древнерусской скорописи // Компьютерная графика и математическое моделирование (Visual Computing): Сб. тез. и докл. науч. школы для молодых учёных. М., 2009. С. 116–131.
3. Чикунов И.М. Электронное издание древних рукописей и первопечатных книг: дис...канд. техн. наук: 05.13.06. М., 2003. 153 с.
4. Baader F. The description logic handbook. Theory, Implementation and Applications
/ F. Baader [и др.]. Cambridge University Press, 2003. URL: http://higherintellect.info/texts/science_and_technology/The%20Description%20Logic%20Handbook%20-%20Theory,%20Implementation%20and%20Applications%20%282003%29.pdf (дата обращения: 05.10.2011).
Публикации с ключевыми словами: распознавание, структурное описание, скоропись, фреймовые сети, гипотезы
Публикации со словами: распознавание, структурное описание, скоропись, фреймовые сети, гипотезы
Смотри также:
- 77-30569/296965 Распознавание букв и слов древнерусской скорописи XVII в.
- Адаптация нейросетевой системы распознавания вертолета по его акустическому излучению к скорости полета
- 77-48211/431251 Метод поиска автомобильных номеров с использованием модификации алгоритма распознавания государственных регистрационных знаков
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||





