научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 004.657
МГТУ им. Н.Э. Баумана
Введение
В некоторых работах [1, 5, 6] для нахождения коэффициентов аналитических выражений, используемых для оценки времени выполнения запросов к базам данных, предлагается использовать калибровочную модель, представляющую собой определённую БД, набор запросов, а также аппаратно-программный комплекс, на котором выполняются калибрующие эксперименты. Предлагаемые аналитические выражения необходимо строить для каждой конфигурации аппаратно-программных средств. Более того, эти выражения не отражают особенностей выполнения сложных запросов SQL. Для проведения расчётов вводятся некоторые сложные интегрированные параметры, при этом не совсем понятна их природа и не указывается, как можно оценить эти параметры.
В работах [2, 7, 8] предлагаются методы оценки стоимостных характеристик различных способов соединения таблиц (NLJ, SMJ, HJ), используемых при выполнении запросов к базе данных. К сожалению, здесь не учитывается случайных характер параметров соединяемых таблиц. Т. е. расчёты ведутся на уровне средних значений. В этих работах также не показано, как можно получить исходные данные для расчётов характеристик соединения промежуточных таблиц, получаемых при реализации оптимального плана выполнения исходного запроса к базе данных.
В данной работе разрабатывается новый математический аппарат анализа времени выполнения запросов SELECTк распределённой базе данных, учитывающий механизмы декомпозиции сложных запросов на подзапросы и соединения результатов их выполнения, параметры логической схемы и случайную природу характеристик наполнения базы данных. Предлагаемый подход можно использовать на ранних этапах проектирования баз данных для оценки временных характеристик выполнения запросов различной степени сложности на различных аппаратно-программных платформах. При этом оценки получаются в виде преобразований Лапласа-Стилтьеса, что позволяет оценивать не только средние величины, но и дисперсии, а также моменты более высоких порядков.
1. Организация обработки запросов SQL
С точки зрения программистов распределённая база данных – это большая виртуальная БД. Оптимизатор запросов (планировщик запросов) СУБД автоматически выполняет декомпозицию запроса на подзапросы и организует их выполнение. При этом оптимизатор выполняет следующие шаги:
1. Исходный запрос преобразуется в формулу реляционной алгебры (явно или нет). Известно, что оператор SELECT языка SQL может быть представлен в виде следующей формулы реляционной алгебры [4]:
πA (σF ( R1 ´ R2 ´ ... ´ Rn )), (1)
где ( R1´R2´ ... ´ Rn ) – декартово произведение отношений (таблиц), указанных за ключевым словом FROM оператора SELECT,σF– операция селекции кортежей декартова произведения в соответствии с условием F, указанным за ключевым словом WHERE, πA– проекции селекции на множество атрибутов А, которые перечисляются за ключевым словом SELECT.
2. Эта формула подвергается оптимизатором улучшению. Смысл улучшения заключается в перемещении операций селекции и проекции внутрь декартова произведения с использованием законов реляционной алгебры и некоторых правил, сформулированных в [4]. В результате формула (1) преобразуется к виду:
![]() (2)
(2)
Здесь![]() ,
, ![]() исходное условие поиска в формуле (1),
исходное условие поиска в формуле (1), ![]() условие соединения результатов выполнения подзапросов
условие соединения результатов выполнения подзапросов ![]() ,
, ![]() условие поиска в i–ом подзапросе. Подчёркнутые в (2) элементы (подзапросы) имеют меньшую размерность, чем исходные отношения R1 и R2.
условие поиска в i–ом подзапросе. Подчёркнутые в (2) элементы (подзапросы) имеют меньшую размерность, чем исходные отношения R1 и R2.
3. В зависимости от настроек, сделанных проектировщиком, оптимизатор использует один из следующих методов построения оптимального плана выполнения запроса на основе формулы, полученной на шаге 2: продукционная или стоимостная оптимизация.
4. При формировании оптимального плана на шаге 3 оптимизатор выбирает метод соединения таблиц. В основном используются следующие методы: соединение с помощью вложенных циклов (NLJ - Nested Loop Joins), соединение посредством сортировки-слияния (SMJ- Sort-Merge Join), хешированное соединение (HJ - Hash Joins), кластерное соединение.
Из выражений (1) и (2) следует, что описание запроса к базе данных и, следовательно, время его выполнения зависят от схемы базы данных. Из анализа работы оптимизаторов следует [3], что построение оптимального плана сводится, в основном, к определению последовательности выполнения соединений промежуточных таблиц, полученных при выполнении подзапросов:
![]() (3)
(3)
здесь ![]() - промежуточная таблица, полученная при выполнении соответствующего подзапроса. Эти таблицы будем обозначать так же, как и подзапросы (см. (2)),
- промежуточная таблица, полученная при выполнении соответствующего подзапроса. Эти таблицы будем обозначать так же, как и подзапросы (см. (2)), ![]() - результирующая таблица, которая соответствует исходному запросу к базе данных. Из (3) следует, что оценка времени выполнения запроса сводится к получению оценок времени обработки подзапросов
- результирующая таблица, которая соответствует исходному запросу к базе данных. Из (3) следует, что оценка времени выполнения запроса сводится к получению оценок времени обработки подзапросов ![]() и построению рекуррентной математической процедуры оценки времени выполнения соединений. Введём некоторые обозначения.
и построению рекуррентной математической процедуры оценки времени выполнения соединений. Введём некоторые обозначения.
1. Пусть ![]() - множество атрибутов таблицы (отношения)
- множество атрибутов таблицы (отношения) ![]() , которые входят в условие (предикат)
, которые входят в условие (предикат) ![]()
![]() -го подзапроса в (2),
-го подзапроса в (2), ![]() . В общем случае на атрибуты
. В общем случае на атрибуты ![]() в условии поиска
в условии поиска ![]() накладываются ограничения, которые могут изменяться при разных обращениях к запросу.
накладываются ограничения, которые могут изменяться при разных обращениях к запросу. ![]() - атрибут из множества
- атрибут из множества ![]() , т. е.
, т. е. ![]() . По определению
. По определению ![]() .
.
2. ![]() - те значения атрибута
- те значения атрибута ![]() , которые удовлетворяют соответствующему элементарному условию по
, которые удовлетворяют соответствующему элементарному условию по ![]() в предикате
в предикате ![]() . Ясно, что
. Ясно, что ![]() , где
, где ![]() - домен (множество значений) атрибута
- домен (множество значений) атрибута ![]() в таблице
в таблице ![]() .
. ![]() - мощность домена. Далее будем использовать следующее множество:
- мощность домена. Далее будем использовать следующее множество:
![]() , (4)
, (4)
4. ![]() - вероятность, что атрибут
- вероятность, что атрибут ![]() какого-нибудь кортежа (записи) таблицы
какого-нибудь кортежа (записи) таблицы ![]() принимает значение
принимает значение ![]() ,
,  . Вероятности
. Вероятности ![]() можно задать априори или получить из гистограмм, которые могут быть построены утилитой СУБД сбора статистик. Для записей из таблиц
можно задать априори или получить из гистограмм, которые могут быть построены утилитой СУБД сбора статистик. Для записей из таблиц ![]() будем считать независимыми в совокупности события
будем считать независимыми в совокупности события
![]() . (5)
. (5)
5. Далее будем использовать преобразование Лапласа-Стилтьеса (Л.-С.) функции распределения случайного времени: 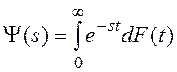 (или просто преобразование Л.-С. времени). Для Л.-С. справедливо равенство:
(или просто преобразование Л.-С. времени). Для Л.-С. справедливо равенство:
![]() ,
,
где ![]() - n-ая производная
- n-ая производная ![]() при
при ![]() ,
, ![]() - n-ый начальный момент случайной величины
- n-ый начальный момент случайной величины ![]() . Например,
. Например, ![]() - это среднее значение,
- это среднее значение, ![]() - дисперсия и т. д.
- дисперсия и т. д.
6. ![]() - производящая функция числа записей в таблице
- производящая функция числа записей в таблице ![]() . Производящая функция дискретной случайной величины
. Производящая функция дискретной случайной величины ![]() с целыми неотрицательными значениями определяется следующим выражением:
с целыми неотрицательными значениями определяется следующим выражением:
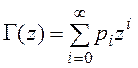 ,
, 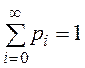 ,
,
где ![]() - вероятность, что случайная величина
- вероятность, что случайная величина ![]() равна i. Имеют место равенства
равна i. Имеют место равенства
![]() ,
, ![]() ,
, ![]() ,
,
где ![]() - n-ая производная
- n-ая производная ![]() в точке
в точке ![]() .
.
2. Оценка времени обработки подзапросов
Этот раздел написан в соавторстве с Плутенко А.Д. Найдём преобразование Л.-С. времени чтения блоков индексов по тем атрибутам из ![]() , для которых при выполнении подзапроса
, для которых при выполнении подзапроса ![]() из (2) используются индексы.
из (2) используются индексы.
Лемма 1. Преобразование Л.-С. времени чтения блоков нижнего уровня по всем используемым в подзапросе ![]() индексам таблицы
индексам таблицы ![]() равно:
равно:
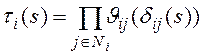 , (6)
, (6)
здесь ![]() - множество тех атрибутов из
- множество тех атрибутов из ![]() , для которых при выполнении подзапроса
, для которых при выполнении подзапроса ![]() используются индексы,
используются индексы, ![]() - преобразование Л.-С. времени чтения одного блока нижнего уровня индекса по атрибуту
- преобразование Л.-С. времени чтения одного блока нижнего уровня индекса по атрибуту ![]() ,
, ![]() - производящая функция читаемых блоков индекса по атрибуту
- производящая функция читаемых блоков индекса по атрибуту ![]() .
.
Если множество элементов ![]() домена
домена ![]() после упорядочивания образуют последовательность смежных значений, то
после упорядочивания образуют последовательность смежных значений, то
 , (7)
, (7)
где ![]() ,
,  ,
, ![]() ,
,
 ,
,
![]() - максимальное число записей в блоке нижнего уровня индекса по атрибуту
- максимальное число записей в блоке нижнего уровня индекса по атрибуту ![]() .
.
В противном случае необходимо определить произведение выражений (7), которые соответствуют участкам смежных значений атрибутов в множестве ![]() . Найдём теперь преобразование Л.-С. времени чтения блоков таблицы
. Найдём теперь преобразование Л.-С. времени чтения блоков таблицы ![]() с записями, удовлетворяющими условию поиска
с записями, удовлетворяющими условию поиска ![]() . Но, прежде всего, определим рекуррентную процедуру расчёта вероятности
. Но, прежде всего, определим рекуррентную процедуру расчёта вероятности ![]() , что произвольная запись таблицы
, что произвольная запись таблицы ![]() удовлетворяет условию поиска
удовлетворяет условию поиска ![]() . Вероятность, что запись таблицы
. Вероятность, что запись таблицы ![]() удовлетворяет элементарному условию поиска по атрибуту
удовлетворяет элементарному условию поиска по атрибуту ![]() в предикате
в предикате ![]() , можно определить с помощью следующего выражения:
, можно определить с помощью следующего выражения:
 (8)
(8)
В частности из (8) следует, что если вероятности ![]() одинаковы, то
одинаковы, то
 , (9)
, (9)
где ![]() - мощность множества
- мощность множества ![]() (см. (4)), а
(см. (4)), а ![]() - мощность домена
- мощность домена ![]() . Элементарные условия по атрибутам
. Элементарные условия по атрибутам ![]() в
в ![]() могут быть связаны различными логическими условиями: AND, OR и может быть NOT. Для расчёта вероятности
могут быть связаны различными логическими условиями: AND, OR и может быть NOT. Для расчёта вероятности ![]() можно воспользоваться рекуррентной процедурой, которая описана в виде табл. 1.
можно воспользоваться рекуррентной процедурой, которая описана в виде табл. 1.
Таблица 1
Условие | Вероятность |
усл.3 = усл.1 AND усл.2 |
|
усл.3 = усл.1 OR усл.2 |
|
усл.2 = NOT(усл.1) |
|
Здесь ![]() ,
, ![]() ,
, ![]() - это вероятности, что запись таблицы
- это вероятности, что запись таблицы ![]() удовлетворяет соответствующему условию. Первоначально "усл.1" и "усл.2" в правой части равенств первого столбца табл. 1 - это элементарные условия в
удовлетворяет соответствующему условию. Первоначально "усл.1" и "усл.2" в правой части равенств первого столбца табл. 1 - это элементарные условия в ![]() , а
, а ![]() и
и ![]() - это вероятности, вычисляемые с помощью выражения (8).
- это вероятности, вычисляемые с помощью выражения (8).
Следует отметить, что ![]() не зависит от числа записей
не зависит от числа записей ![]() в таблице
в таблице ![]() , т. к. от
, т. к. от ![]() не зависят вероятности
не зависят вероятности![]() (см. (8)). Применяя схему Бернулли с параметром
(см. (8)). Применяя схему Бернулли с параметром ![]() и используя формулу полной вероятности, найдём производящую функцию числа записей таблицы
и используя формулу полной вероятности, найдём производящую функцию числа записей таблицы ![]() , удовлетворяющих условию поиска
, удовлетворяющих условию поиска ![]() :
:
 , (10)
, (10)
здесь ![]() - вероятность, которая определяется с помощью описанной выше рекуррентной процедуры (см. табл. 1),
- вероятность, которая определяется с помощью описанной выше рекуррентной процедуры (см. табл. 1), ![]() - производящая функция числа записей в таблице
- производящая функция числа записей в таблице ![]() .
.
Лемма 2. Преобразование Л.-С. времени чтения блоков таблицы ![]() с записями, удовлетворяющими условию поиска
с записями, удовлетворяющими условию поиска ![]() , имеет вид
, имеет вид
![]() , (11)
, (11)
где ![]() - преобразование Л.-С. времени чтения одного блока таблицы
- преобразование Л.-С. времени чтения одного блока таблицы ![]() ,
, ![]() - производящая функция читаемых блоков таблицы
- производящая функция читаемых блоков таблицы ![]() .
.
Если записи, удовлетворяющие условию поиска ![]() , располагаются в блоках таблицы
, располагаются в блоках таблицы ![]() последовательно (в соседних строках), то
последовательно (в соседних строках), то
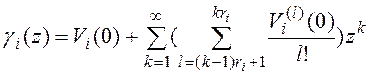 , (12)
, (12)
здесь ![]() определяется выражением (10),
определяется выражением (10), ![]() - максимальное число записей в блоке таблицы
- максимальное число записей в блоке таблицы ![]() . В общем случае, если записи, удовлетворяющие условию поиска
. В общем случае, если записи, удовлетворяющие условию поиска ![]() , не располагаются в блоках таблицы
, не располагаются в блоках таблицы ![]() последовательно (в соседних строках), то производящую функцию читаемых блоков таблицы
последовательно (в соседних строках), то производящую функцию читаемых блоков таблицы ![]() можно найти с помощью произведения выражений вида (12), которые соответствуют участкам с последовательным размещением записей в блоках.
можно найти с помощью произведения выражений вида (12), которые соответствуют участкам с последовательным размещением записей в блоках.
Теорема 1. Для преобразования Л.-С. времени выполнения подзапроса ![]() справедливо следующее выражение:
справедливо следующее выражение:
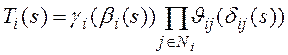 , (13)
, (13)
где ![]() - множество тех атрибутов из
- множество тех атрибутов из ![]() , для которых при выполнении подзапроса
, для которых при выполнении подзапроса ![]() используются индексы,
используются индексы, ![]() - преобразование Л.-С. времени чтения одного блока нижнего уровня индекса по атрибуту
- преобразование Л.-С. времени чтения одного блока нижнего уровня индекса по атрибуту ![]() ,
, ![]() - производящая функция читаемых блоков индекса по атрибуту
- производящая функция читаемых блоков индекса по атрибуту ![]() , которая определяется выражением (7),
, которая определяется выражением (7), ![]() - преобразование Л.-С. времени чтения одного блока таблицы
- преобразование Л.-С. времени чтения одного блока таблицы ![]() ,
, ![]() - производящая функция читаемых блоков таблицы
- производящая функция читаемых блоков таблицы ![]() , которая определяется выражением (12).
, которая определяется выражением (12).
Утверждение теоремы 1 следует из формул (6) и (11), являющихся утверждениями лемм 1 и 2, и свойств преобразования Л.-С..
3. Рекуррентная формула для определения производящей функции числа кортежей соединяемых таблиц
Соединение промежуточных таблиц ![]() выполняется попарно в последовательности, определённой при построении оптимального плана (см. (3)).
выполняется попарно в последовательности, определённой при построении оптимального плана (см. (3)).
Соединение является рекуррентной математической процедурой: ![]() ,
, ![]() . Первоначально
. Первоначально ![]() . Далее без потери общности будем считать, что
. Далее без потери общности будем считать, что ![]() . Будем также полагать, что
. Будем также полагать, что ![]() - это множество всех атрибутов какой-нибудь соединяемой таблицы. Для оценки времени соединения таблиц (раздел 4) на каждом шаге рекуррентной процедуры необходимо выполнить следующие действия:
- это множество всех атрибутов какой-нибудь соединяемой таблицы. Для оценки времени соединения таблиц (раздел 4) на каждом шаге рекуррентной процедуры необходимо выполнить следующие действия:
1. Найти производящую функцию числа записей и множество атрибутов для каждой из двух соединяемых таблиц.
2. Для каждого атрибута ![]() соединяемых таблиц определить его домен
соединяемых таблиц определить его домен ![]() и вероятности
и вероятности ![]() .
.
Сначала покажем, как указанные выше задачи 1 и 2 решаются для соединяемых таблиц ![]() , которые соответствуют подзапросам.
, которые соответствуют подзапросам.
1. Производящая функция для числа записей определяется выражением (10), а множество атрибутов совпадает с ![]() (см. (2)).
(см. (2)).
2. Представим условие ![]() в виде дизъюнктивной формы. Домен
в виде дизъюнктивной формы. Домен ![]() атрибута
атрибута ![]() в таблице
в таблице ![]() определим следующим образом:
определим следующим образом:
а) если атрибут входит во все конъюнкты дизъюнктивной формы, то в этом случае полагаем
 , (14)
, (14)
![]() - это те значения атрибута
- это те значения атрибута ![]() , которые удовлетворяют элементарному условию по
, которые удовлетворяют элементарному условию по ![]() в конъюнкте с номером
в конъюнкте с номером ![]() ,
,
б) иначе домен атрибута оставляем без изменения (как в таблице ![]() ).
).
Если домен атрибута изменился (см. (14)), то необходимо выполнить "нормирование" вероятностей элементов нового домена ![]() :
:
 ,
, ![]() (15)
(15)
Покажем теперь, как
1) найти производящую функцию числа записей в промежуточной таблице ![]() , которая, в свою очередь, может соединяться с таблицей
, которая, в свою очередь, может соединяться с таблицей ![]() , а также множество атрибутов в таблице
, а также множество атрибутов в таблице ![]() ,
,
2) определить домены ![]() атрибутов
атрибутов ![]() , добавленных в таблицу
, добавленных в таблицу ![]() в результате соединения, и вероятности
в результате соединения, и вероятности ![]() .
.
Без потери общности будем считать, что соединяются таблицы ![]() и
и ![]() , т. е.
, т. е. ![]() , т. к. далее рекуррентно можно положить
, т. к. далее рекуррентно можно положить ![]() и
и ![]() ,
, ![]() . Рассмотрим общий случай соединения таблиц по нескольким атрибутам. Без потери общности будем считать, что таблицы
. Рассмотрим общий случай соединения таблиц по нескольким атрибутам. Без потери общности будем считать, что таблицы ![]() и
и ![]() соединяются соответственно по атрибутам
соединяются соответственно по атрибутам ![]() и
и ![]() . Пусть
. Пусть ![]() - условие связи между этими группами атрибутов.
- условие связи между этими группами атрибутов.
В дальнейшем под соединяемыми записями таблиц ![]() и
и ![]() будем понимать записи этих таблиц, в которых значения атрибутов связи {
будем понимать записи этих таблиц, в которых значения атрибутов связи {![]() ,...,
,..., ![]() } и {
} и {![]() ,...,
,..., ![]() } связаны отношением
} связаны отношением ![]() , т. е.
, т. е. ![]() , где
, где ![]() - условие связи таблиц
- условие связи таблиц ![]() и
и ![]() по атрибутам связи
по атрибутам связи ![]() и
и ![]() (=, <,
(=, <, ![]() , >,
, >, ![]() ,
, ![]() или более сложное условие). Под группой соединяемых записей будем понимать совокупность соединяемых записей таблицы
или более сложное условие). Под группой соединяемых записей будем понимать совокупность соединяемых записей таблицы ![]() (или
(или ![]() ), в которых атрибуты связи
), в которых атрибуты связи ![]() (или
(или ![]() ) принимают одинаковые значения, т. е. имеют одинаковые подстроки в соответствующей таблице.
) принимают одинаковые значения, т. е. имеют одинаковые подстроки в соответствующей таблице.
Лемма 4. Пусть количества кортежей в разных группах соединяемых записей таблиц ![]() и
и ![]() независимы в совокупности. Тогда справедливы следующие утверждения:
независимы в совокупности. Тогда справедливы следующие утверждения:
1. Производящая функция числа записей в таблице ![]() имеет следующий вид:
имеет следующий вид:
 (16)
(16)
где 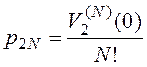 - вероятность, что число записей в таблице
- вероятность, что число записей в таблице ![]() равно
равно ![]() (см. свойства производящей функции в разделе 1),
(см. свойства производящей функции в разделе 1),
![]() - производящая функция числа записей таблицы
- производящая функция числа записей таблицы ![]() ,
, ![]() - производящая функция числа записей таблицы
- производящая функция числа записей таблицы ![]() ,
,
![]() ,
, ![]() - это отношение связи таблиц
- это отношение связи таблиц ![]() и
и ![]() по атрибутам связи
по атрибутам связи ![]() и
и ![]() (=, <,
(=, <, ![]() , >,
, >, ![]() ,
, ![]() или более сложное условие).
или более сложное условие).
Множество атрибутов таблицы ![]() равно
равно ![]() , где
, где ![]() и
и ![]() - множества атрибутов таблиц
- множества атрибутов таблиц ![]() и
и ![]() .
.
2. Для доменов атрибутов связи ![]() и
и ![]() , вошедших в
, вошедших в ![]() , справедливы следующие выражения:
, справедливы следующие выражения:
 (17)
(17)

Вероятности появления элементов доменов ![]() и
и ![]() в кортежах таблицы
в кортежах таблицы ![]() равны
равны
 ,
, ![]() ,
, ![]() , (18)
, (18)
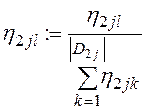 ,
, ![]() ,
, ![]() .
.
Домены остальных атрибутов таблицы ![]() и вероятности появления элементов этих доменов в кортежах
и вероятности появления элементов этих доменов в кортежах ![]() не изменяются.
не изменяются.
4. Оценка времени выполнения соединения таблиц
В этом разделе выводятся преобразования Л.-С. времени соединения ![]() , которое может быть выполнено оптимизатором с помощью одного из методов, указанных в разделе 1. Производящие функции
, которое может быть выполнено оптимизатором с помощью одного из методов, указанных в разделе 1. Производящие функции ![]() и
и ![]() числа записей в соединяемых таблицах
числа записей в соединяемых таблицах ![]() и
и ![]() были получены в разделах 2 и 3 (см. формулы (10) и (16)). Производящая функция числа записей
были получены в разделах 2 и 3 (см. формулы (10) и (16)). Производящая функция числа записей ![]() в таблице
в таблице ![]() была получена в разделе 3 (см. рекуррентную формулу (16)).
была получена в разделе 3 (см. рекуррентную формулу (16)).
4.1. Метод соединения с помощью вложенных циклов NLJ
Теорема 2. Преобразование Л.-С. времени ![]() выполнения соединения таблиц
выполнения соединения таблиц ![]() и
и ![]() методом NLJ имеет вид:
методом NLJ имеет вид:
![]() , (19)
, (19)
где ![]() ,
, ![]() ,
, ![]() - производящие функции числа записей в таблицах
- производящие функции числа записей в таблицах ![]() ,
, ![]() и
и ![]() ,
, ![]() - преобразование Л.-С. времени сравнения атрибутов связи двух кортежей из
- преобразование Л.-С. времени сравнения атрибутов связи двух кортежей из ![]() и
и ![]() ,
, ![]() - преобразование Л.-С. времени соединения двух кортежей из
- преобразование Л.-С. времени соединения двух кортежей из ![]() и
и ![]() .
.
4.2. Метод соединение посредством сортировки-слияния SMJ
Сначала таблицы ![]() и
и ![]() при необходимости сортируются по атрибутам связи, а затем выполняется их соединение. Предположим, что сортировка выполняется в порядке возрастания атрибута связи и элементы домена этого атрибута также упорядочены в порядке возрастания:
при необходимости сортируются по атрибутам связи, а затем выполняется их соединение. Предположим, что сортировка выполняется в порядке возрастания атрибута связи и элементы домена этого атрибута также упорядочены в порядке возрастания: ![]() <
< ![]() < ... <
< ... < ![]() , здесь
, здесь ![]() - мощность домена
- мощность домена ![]() ,
, ![]() . Также предположим, что сортировка выполняется обычным способом: путём перемещения влево
. Также предположим, что сортировка выполняется обычным способом: путём перемещения влево ![]() -ой записи внутрь уже упорядоченных
-ой записи внутрь уже упорядоченных ![]() записей (пузырьковый способ).
записей (пузырьковый способ).
Лемма 5. Пусть число перемещений записей на ![]() -ом шаге не зависит от числа перемещений на предыдущих шагах. Тогда производящая функция числа перемещений при сортировке записей таблицы
-ом шаге не зависит от числа перемещений на предыдущих шагах. Тогда производящая функция числа перемещений при сортировке записей таблицы ![]() по атрибуту связи
по атрибуту связи ![]() имеет вид
имеет вид
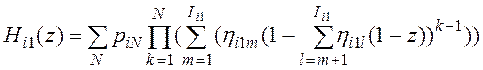 , (20)
, (20)
здесь ![]() - вероятность, что количество записей в таблице
- вероятность, что количество записей в таблице ![]() равно N.
равно N.
Теперь найдём производящую функцию числа сравнений атрибутов связи соединяемых таблиц ![]() и
и ![]() .
.
Лемма 6. Производящая функция количества сравнений атрибутов связи при соединении таблиц ![]() и
и ![]() имеет следующий вид:
имеет следующий вид:
 , (21)
, (21)
здесь
 ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() - производящая функция числа записей в таблице
- производящая функция числа записей в таблице ![]() ,
, ![]() (см. формулы (10) и (16)).
(см. формулы (10) и (16)).
Теорема 3. Преобразование Л.-С. времени ![]() выполнения соединения таблиц
выполнения соединения таблиц ![]() и
и ![]() методом SMJ имеет вид:
методом SMJ имеет вид:
![]() , (22)
, (22)
![]() - производящая функция числа перемещений при сортировке записей таблицы
- производящая функция числа перемещений при сортировке записей таблицы ![]() по атрибуту связи
по атрибуту связи ![]() , которая определяется выражением (20),
, которая определяется выражением (20), ![]() ,
, ![]() - производящая функция количества сравнений атрибутов связи при соединении таблиц
- производящая функция количества сравнений атрибутов связи при соединении таблиц ![]() и
и ![]() , которая определяется выражением (21),
, которая определяется выражением (21), ![]() - производящая функция числа записей в таблице
- производящая функция числа записей в таблице ![]() (см. формулу (16)),
(см. формулу (16)), ![]() - преобразование Л.-С. времени перемещения двух кортежей при сортировке таблиц
- преобразование Л.-С. времени перемещения двух кортежей при сортировке таблиц ![]() и
и ![]() ,
, ![]() - преобразование Л.-С. времени сравнения атрибутов связи двух кортежей из
- преобразование Л.-С. времени сравнения атрибутов связи двух кортежей из ![]() и
и ![]() ,
, ![]() - преобразование Л.-С. времени соединения двух кортежей из
- преобразование Л.-С. времени соединения двух кортежей из ![]() и
и ![]() .
.
4.3. Метод хешированного соединения HJ
В процессе хешированного соединения выполняются следующие шаги:
1. Выбирается хеш-функция.
2. Записи соединяемых таблиц ![]() и
и ![]() хешируются по атрибутам связи, т. е. создаются две группы таблиц
хешируются по атрибутам связи, т. е. создаются две группы таблиц ![]() ,
, ![]() , число таблиц в группе равно количеству разделов.
, число таблиц в группе равно количеству разделов.
3. Для каждого раздела с помощью метода SMJ или NLJ выполняется соединение таблиц соответствующих таблиц: ![]() ,
, ![]() ,
, ![]() - число разделов.
- число разделов.
4. Объединяются результаты соединений, выполненных на шаге 3: 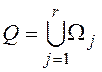 .
.
В качестве хеш-функции можно выбрать, например, деление по модулю 10 значений атрибутов связи. В этом случае число разделов ![]() (число различных остатков от деления на 10) и в таблицу
(число различных остатков от деления на 10) и в таблицу ![]() попадут записи таблицы
попадут записи таблицы ![]() , для которых остаток от деления на 10 значения атрибута связи равен
, для которых остаток от деления на 10 значения атрибута связи равен ![]() (
(![]() ).
).
Лемма 7. Справедливы следующие утверждения:
1. Производящая функция числа записей в таблице ![]() (
(![]() ,
, ![]() ) имеет вид
) имеет вид
 , (23)
, (23)
здесь ![]() - производящая функция числа записей в таблице
- производящая функция числа записей в таблице ![]() ,
, ![]() ,
, ![]() - хеш-функция, которая возвращает номер раздела,
- хеш-функция, которая возвращает номер раздела, ![]() - элемент домена
- элемент домена ![]() атрибута связи
атрибута связи ![]() таблицы
таблицы ![]() .
.
2. Домен атрибута связи ![]() таблицы
таблицы ![]() включает следующие элементы:
включает следующие элементы:
![]() . (24)
. (24)
Вероятности появления элементов доменов ![]() в кортежах таблицы
в кортежах таблицы ![]() равны
равны
 ,
, ![]() ,
, ![]() ,
, ![]() , (25)
, (25)
здесь в правой части ![]() .
.
Домены остальных атрибутов таблицы ![]() , вошедших в
, вошедших в ![]() из
из ![]() , и вероятности появления элементов этих доменов в кортежах
, и вероятности появления элементов этих доменов в кортежах ![]() не изменяются.
не изменяются.
Теорема 4. Преобразование Л.-С. времени ![]() выполнения соединения таблиц
выполнения соединения таблиц ![]() и
и ![]() методом HJ имеет вид:
методом HJ имеет вид:
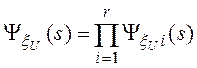 , (26)
, (26)
где ![]() - число разделов,
- число разделов, ![]() - это преобразование Л.-С. времени соединения таблиц
- это преобразование Л.-С. времени соединения таблиц ![]() и
и ![]() , выполненного методом NLJили SMJ. Формулы для
, выполненного методом NLJили SMJ. Формулы для ![]() определяются выражениями (19) или (22). Производящие функции числа записей соединяемых таблиц
определяются выражениями (19) или (22). Производящие функции числа записей соединяемых таблиц ![]() и
и ![]() , а также домены атрибутов связи определяются выражениями (23) и (24),
, а также домены атрибутов связи определяются выражениями (23) и (24), ![]() .
.
Доказательство теоремы 4 следует из описания алгоритма хешированного соединения, леммы 7 и свойств преобразования Л.-С.
5. Оценка времени выполнения исходного запроса SQL
На основании результатов, сформулированных в предыдущих разделах, можно получить преобразование Л.-С. времени выполнения исходного запроса (3).
Теорема 5. Преобразование Л.-С. времени выполнения исходного запроса (3) имеет следующий вид:
 , (27)
, (27)
где ![]() - это преобразование Л.-С. времени выполнения подзапроса
- это преобразование Л.-С. времени выполнения подзапроса ![]() , которое определяется выражением (13),
, которое определяется выражением (13), ![]() - преобразование Л.-С. времени
- преобразование Л.-С. времени ![]() -го соединения промежуточных таблиц, которое определяет одним из выражений (19), (22) и (26) (тип соединения назначается оптимизатором для каждого
-го соединения промежуточных таблиц, которое определяет одним из выражений (19), (22) и (26) (тип соединения назначается оптимизатором для каждого![]() -го соединения),
-го соединения), ![]() - число подзапросов в (3).
- число подзапросов в (3).
Доказательство теоремы 5 следует из свойств преобразования Л.-С. и теорем 1, 2, 3, 4, приведённых в предыдущих разделах. Используя выражение (27), можно оценивать различные моменты (среднее, дисперсию и др.) времени выполнения запросов SQL.
Важно подчеркнуть, что полученные выражения для преобразований Л.-С. времени выполнения подзапросов (13) и соединений (19), (22), (26), а также для производящих функций числа кортежей в исходных и результирующих таблицах (см. формулы (10) и (16)) могут быть использованы не только для расчёта характеристик времени выполнения запросов SQL (27), но и для оценки параметров функций распределений при подготовке исходных данных моделей массового обслуживания, которые часто используются для анализа показателей качества распределённых систем обработки данных на макроуровне.
Предложенный математический аппарат был использован при разработке Комплекса инструментальных Средств Анализа Моделей доступа к базам данных распределённых систем обработки данных (КСАМ). Этот комплекс относится к классу экспертных систем и предназначен для проведения вычислительных экспериментов с целью анализа временных показателей систем, основу которых составляют распределённые базы данных и приложения.
СПИСОК ЛИТЕРАТУРЫ
1. WeiminDu, RaviKrishnamurthy, Ming-ChienShan. Query Optimization in a Heterogeneous DBMS // Proceedings of 18th International Conference on Very Large Data Bases, August 23-27, 1992, Vancouver, Canada. - P. 277-291.
2. Goetz Graefe. Query Evaluation Techniques for Large Databases // ACM Computing Surveys. - 1993. - Vol. 25, № 2. - P. 73-170.
3. Чаудхари С. Методы оптимизации запросов в реляционных системах // Системы управления базами данных. - М., 1998. - № 3. - С. 22-36.
4. Ульман Дж. Основы систем баз данных. – М.: Финансы и статистика, 1983. – 334 с.
5. Georges Gardarin, Jean-Robert Gruser, Zhao-Hui Tang. Cost-based Selection of Path Expression Processing Algorithms in Object-Oriented Databases // Proceedings of 22th International Conference on Very Large Data Bases (VLDB'96), September 3-6, 1996, Mumbai (Bombay), India. - P. 390-401.
6. G. Gardarin, F. Sha, and Z.-H. Tang. Calibrating the query optimizer cost model of IRO-DB, an objectoriented federated database system // Proceedings of 22th International Conference on Very Large Data Bases (VLDB'96), September 3-6, 1996, Mumbai (Bombay), India. - P. 378--389.
7. Mishra P., Eich M.H. Join Processing in relational databases. // ACM Computing Surveys. - 1992. - Vol. 24, № 1.
8. E. P. Harris, K. Ramamohanarao. Join algorithm costs revisited // The VLDB Journal. - 1996. - Vol. 5, № 1. - P. 64--84.
Публикации с ключевыми словами: база данных, преобразование Лапласа-Стилтьеса, оптимизация оператора SELECT, запрос SQL, время выполнения запроса, производящая функция
Публикации со словами: база данных, преобразование Лапласа-Стилтьеса, оптимизация оператора SELECT, запрос SQL, время выполнения запроса, производящая функция
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



