научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК 004.436.4
МГТУ им. Н.Э. Баумана
Поскольку изложение материала статьи опирается на определение алгоритмической модели процесса, кратко изложим содержание этого понятия.
Процесс Z есть четверка [1]:
Z=< S, T, F, a >
где:
S - пространство состояний системы, определенное ранее;
T - множество моментов времени изменения состояний системы;
F – график процесса, определяемый как отображение T→S, причем это отображение должно быть функциональным (однозначным);
α- отношение линейного порядка на T.
Пусть имеем объект Ol в системе Q. Тогда генерация процесса ![]() может быть выполнена путем задания оператора
может быть выполнена путем задания оператора ![]() [1]:
[1]:
где: ![]() ;
;
A - множество аргументов: A![]() Q;
Q;
ω- случайное число.
Остальные определения опираются на материал [2].
В ходе развития процесса совокупность аргументов во множестве ![]() может изменяться. Таким образом, состав элементов множества
может изменяться. Таким образом, состав элементов множества ![]() в общем случае зависит от времени. Обозначим эту зависимость как
в общем случае зависит от времени. Обозначим эту зависимость как ![]() . Рассмотрим два объекта Ol и Om в системе Q. Пусть
. Рассмотрим два объекта Ol и Om в системе Q. Пусть ![]() , а процессы в них заданы следующими операторами:
, а процессы в них заданы следующими операторами:
![]() .
.
Если ![]() и
и ![]() , то такие процессы и объекты называются не сцепленными в момент времени ti.
, то такие процессы и объекты называются не сцепленными в момент времени ti.
Если 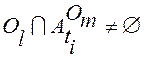 , то объект Om сцеплен с объектом Ol в момент времени ti. То же относится и к их процессам. Это означает, что для определения состояния объекта Om в момент времени ti, необходимо знание состояния объекта Ol в это же время. Обозначим отношение сцепления как Ol→Om. Не следует смешивать отношение сцепления и зависимости. Так, если Om→Ol и Ol→Ok, то вовсе не обязательно, чтобы Om→Ok. Таким образом, отношение сцепления не является транзитивным.
, то объект Om сцеплен с объектом Ol в момент времени ti. То же относится и к их процессам. Это означает, что для определения состояния объекта Om в момент времени ti, необходимо знание состояния объекта Ol в это же время. Обозначим отношение сцепления как Ol→Om. Не следует смешивать отношение сцепления и зависимости. Так, если Om→Ol и Ol→Ok, то вовсе не обязательно, чтобы Om→Ok. Таким образом, отношение сцепления не является транзитивным.
Если к отношению сцепления добавить полное транзитивное замыкание, то получим отношение зависимости. Т.е. если Ol зависит от Om, а Ok зависит от Ol, то Ok зависит и от Om. Таким образом, отношение сцепления можно определить как отношение непосредственной зависимости.
Предлагается задавать оператор Hв виде некоторой алгоритмической структуры.
Рассмотрим дискретный во времени процесс Z. Пространство состояний S может быть как непрерывным, так и дискретным. Поставим в соответствие каждой i-ой точке процесса (момент времени изменения состояния ti) некоторый оператор ![]() . Оператор
. Оператор ![]() вычисляет значение состояния
вычисляет значение состояния ![]() в момент времени ti:
в момент времени ti:
![]() .
.
Оператор ![]() описывает вычисление только одной i-й точки процесса Z. В силу этого условия будем в дальнейшем называть этот оператор элементарным.
описывает вычисление только одной i-й точки процесса Z. В силу этого условия будем в дальнейшем называть этот оператор элементарным.
Таким образом, если график процесса содержит n точек, то мы должны задать линейную последовательность элементарных операторов:
![]() .
.
Введем новый элемент модели - инициатор. Он обладает свойствами динамичности и инициативности. Динамичность - инициатор имеет возможность перемещаться от оператора к оператору; будем называть попадание инициатора на оператор сцеплением инициатора с элементарным оператором. Инициативность - в момент сцепления инициатора с оператором происходит выполнение (инициирование) элементарного оператора, что соответствует вычислению нового состояния процесса. При этом полагаем, что выполнение элементарного оператора происходит мгновенно. Таким образом, описание процесса может быть выполнено путем задания линейной последовательности операторов 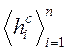 и перемещения по этой последовательности инициатора I, сцепляющегося с элементарными операторами
и перемещения по этой последовательности инициатора I, сцепляющегося с элементарными операторами ![]() в заданные моменты времени ti изменения состояния процесса. Алгоритмическая модель описания процесса предполагает, что моменты сцепления инициатора с элементарными операторами определяют сами элементарные операторы. С этой целью вводится оператор условия сцепления инициатора
в заданные моменты времени ti изменения состояния процесса. Алгоритмическая модель описания процесса предполагает, что моменты сцепления инициатора с элементарными операторами определяют сами элементарные операторы. С этой целью вводится оператор условия сцепления инициатора ![]() , который определяет условие, при выполнении которого инициатор сцепляется со следующим оператором
, который определяет условие, при выполнении которого инициатор сцепляется со следующим оператором ![]() . Возможны следующие варианты задания такого условия:
. Возможны следующие варианты задания такого условия:
а) указание момента времени сцепления инициатора с оператором ![]() ;
;
б) определение логического условия, при выполнении которого инициатор сцепляется с оператором ![]() .
.
Таким образом, определим элементарный оператор hi, как двойку:
![]() .
.
При сцеплении инициатора с элементарным оператором hi происходит мгновенное выполнение его обеих составных частей: выполнение ![]() позволяет вычислить новое состояние si процесса Z, а выполнение оператора
позволяет вычислить новое состояние si процесса Z, а выполнение оператора ![]() дает возможность определить момент времени, либо логическое условие сцепления инициатора со следующим элементарным оператором hi+1. Линейную последовательность элементарных операторов назовем треком TR:
дает возможность определить момент времени, либо логическое условие сцепления инициатора со следующим элементарным оператором hi+1. Линейную последовательность элементарных операторов назовем треком TR:
 .
.
Таким образом, можно АМП определить как двойку:
АМП=<TR,I>.
Построение имитационной модели информационной системы выполняется на основе алгоритмического описания процессов функционирования, таким образом, модель описания параллельных процессов позволяет выполнить исследование в области методов построения имитационных моделей. Имитационный процесс рассматривается, как один последовательный вычислительный процесс, на который отображается система параллельных взаимосвязанных процессов.
Пусть заданы два элементарных оператора hl и hk одного процесса Z, причем hl→hk, (hk сцеплен с hl.).
Утверждение 1. Если hl→hk, то
а) tk≥tl
б) первым должен вычисляться оператор hl.
Рассмотрим влияние отношения сцепления на последовательность выполнения операторов при моделировании. Пусть заданы два процесса Z1 и Z2, условно изображенные на рис. 1.

Рисунок 1. Пример сцепления процессов
Дискретные состояния процесса Z1 пронумерованы от 1 до 13, а процесса Z2 - от 14 до 26. Рассмотрим четыре типовых случая:
а) моделируется один процесс Z1, причем его операторы не сцеплены между собой.
б) моделируется процесс Z1 без ограничения на сцепленность элементарных операторов;
в) моделируются два процесса Z1 и Z2, при этом эти процессы не сцеплены между собой;
г) моделируются два сцепленных процесса Z1 и Z1
На рис. 1 стрелками указано отношение сцепления.
A. Моделирование процесса Z1 при несцепленных операторах hi (∀i).
Поскольку сцепление hi→hi+1 отсутствует для всех i, то последовательность вычислений элементарных операторов не имеет значения и операторы hi (∀i). могут вычисляться в любом порядке.
Б. Моделирование процесса Z1 в общем случае наличия сцепленности.
Естественно предположить, что последовательные состояния одного процесса сцеплены между собой.
Предположим, что hi→hi+1, для всех ![]() . Из утверждения 1 следует, что в таком случае ti+1>ti для всех
. Из утверждения 1 следует, что в таком случае ti+1>ti для всех ![]() . Таким образом, последовательность сцепленных операторов строго следует порядку α на T. Из этого же утверждения следует, что последовательность вычислений операторов должна определяться этим же порядком.
. Таким образом, последовательность сцепленных операторов строго следует порядку α на T. Из этого же утверждения следует, что последовательность вычислений операторов должна определяться этим же порядком.
В. Моделирование несцепленных между собой процессов Z1 и Z2.
Предполагаем, что процессы Z1 и Z2 в отдельности представлены общим случаем. Если hi1 - операторы процесса Z1, а hj2 - операторы процесса Z2, то по предположению отсутствует сцепление между hi1 и hj2 для всех i и j. Так же, как и в случае А, здесь последовательность вычислений элементарных операторов из разных процессов не имеет значения. Однако, поскольку все hi1 сцеплены между собой, и все hj2 также сцеплены между собой, важно, чтобы в этой последовательности выполнялся порядок a1 для процесса Z1 и a2 для процесса Z2. В частности, возможен вариант вычисления сначала всех операторов процесса Z1, а затем всех операторов процесса Z2. Очевидно, что порядок α1 и α2 при этом сохраняется.
Г. Моделирование сцепленных между собой процессов Z1 и Z2. Пример сцепления показан на рис. 1.
В этом случае должен быть обязательно выдержан порядок α1 для Z1 и α2 для Z2, поскольку в общем случае внутри каждого процесса существует сцепленность элементарных операторов. Кроме того, необходимо выполнить условия Утверждения 1 для любой пары сцепленных операторов из разных процессов. Так, для приведенного на рисунке 1 примера в соответствие с условиями Утверждения 1, из операторов h1 и h14 первым должен вычисляться оператор h1, из h5 и h18 первым - h18 и т.д.
Получим возможный порядок вычислений: h1, h14, (h2, h15), (h3, h16), h17, h4 и т.д.
В скобках указаны пары операторов из разных процессов, для которых можно поменять порядок вычислений.
На основании проведенного анализа можно сделать следующие выводы:
1. Для каждого процесса в ходе вычисления операторов необходимо строго придерживаться порядка a на Т.
2. Выполнение п.1. обеспечивает реализацию сцепленности операторов hi→hj, если ti<tj , в рамках реализации одного процесса.
3. При выполнении п.1 указание сцепленности операторов с разным значением ti в рамках одного процесса не добавляет новых ограничений на порядок расчета и может быть опущено.
Действительно, если вычислены элементарные операторы h10 и h23 в момент времени t10, то указание h23→h11 не меняет порядок вычислений, поскольку к моменту времени t11 будет рассчитан оператор h23. При этом условие сцепленности выполняется автоматически.
4. Для определения порядка расчета операторов, принадлежащих разным процессам, важно знание отношения сцепления для операторов разных процессов с одинаковым значением времени ti.
Таким образом, можно сформулировать следующий алгоритм определения порядка вычисления элементарных операторов для совокупности параллельных процессов.
Пусть заданы треки процессов Zi (![]() ):
): ![]() для всех i. Пусть текущее значение времени равно t и все элементарные операторы hi, у которых ti≤t , вычислены. Для всех hij , имеющих ti=t и обладающих условным временным оператором
для всех i. Пусть текущее значение времени равно t и все элементарные операторы hi, у которых ti≤t , вычислены. Для всех hij , имеющих ti=t и обладающих условным временным оператором ![]() , определим для каждого очередной момент времени tij+1 cцепления инициатора по своему треку, задаваемый этим временным оператором. Получим множество
, определим для каждого очередной момент времени tij+1 cцепления инициатора по своему треку, задаваемый этим временным оператором. Получим множество ![]() . Назовем его активным временным множеством.
. Назовем его активным временным множеством.
Это множество содержит по одному значению от каждого процесса, остановленного на элементарном операторе, содержащем временное условие продвижения инициатора. Определим очередное значение времени по формуле:
| (1) |
Последовательное применение формулы строит упорядоченное множество ![]() , где αt -линейный порядок на Tt. Докажем ряд его свойств.
, где αt -линейный порядок на Tt. Докажем ряд его свойств.
Для процесса Zi имеем множество Ti и линейный порядок αi (![]() ). Рассмотрим множество
). Рассмотрим множество ![]() и порядок αT на T, полученный транзитивным замыканием порядков αi.
и порядок αT на T, полученный транзитивным замыканием порядков αi.
Утверждение 2. Множества Tt и T равны.
В самом деле, любой элемент t∈Tt был определен из множества ![]() , элементы которого принадлежат Ti (
, элементы которого принадлежат Ti (![]() ). Поскольку
). Поскольку ![]() , то они же принадлежат и T. Следовательно, каждый элемент множества Ttпринадлежит и множеству T. Аналогично доказывается, что если элемент принадлежит T, то он же принадлежит и Tt. Таким образом, утверждение 2 доказано.
, то они же принадлежат и T. Следовательно, каждый элемент множества Ttпринадлежит и множеству T. Аналогично доказывается, что если элемент принадлежит T, то он же принадлежит и Tt. Таким образом, утверждение 2 доказано.
Утверждение 3. На упорядоченном множестве ![]() сохраняются все порядки ai (
сохраняются все порядки ai (![]() ).
).
Рассмотрим множество Ti с порядком αi. Возьмем два любых его элемента tik и til. Пусть в соответствие с αi tik<til;. Тогда, в соответствие с (2.14) tik окажется минимальным элементом в {tij+1} раньше, чем ti1, и следовательно, войдет во множество Tt раньше, чем ti1. Поскольку упорядочение в Tt определяется порядком поступления элементов в Tt, то, следовательно, и в Tt tik<ti1. Аналогично можно провести доказательство и для остальных процессов. Таким образом, утверждение 3 доказано.
На основании Утверждений 2 и 3 можно сделать заключение о том, что формула 1 позволяет построить новое множество T, включающее все элементы множеств Ti (∀i) , и провести упорядочение его элементов таким образом, что сохраняются все отношения порядка в каждом из них. Поскольку каждому t∈Ti (∀i) ставится в соответствие свой элементарный оператор в треке, то определение порядка на T дает возможность однозначно определить порядок на всем множестве элементарных операторов заданных процессов.
Рассмотрим последовательность выполнения элементарных операторов в системе. Пусть система содержит 9 объектов, в каждом из которых развивается процесс. На рис. 2 приведен пример организации треков на некотором временном интервале. Пусть в некоторый момент времени система находилась в состоянии, показанном на рис. 2 слева. Назовем его начальным состоянием.

Рисунок 2. Пример реализации процессов через события
Для каждого процесса Zi указан текущий элементарный оператор в следующих обозначениях:
![]()
где i -номер процесса (он же- номер строки);
n -порядковый номер элементарного оператора в своем треке;
с -символ “состояние”;
у=л - символ логического условия продвижения инициатора;
у=t - символ временного условия продвижения инициатора.
Предположим, что к этому моменту времени все элементарные операторы вычислены. Тогда активное временное множество на текущий момент равно {t110, t311, t621, t926,}
Определим в соответствии с (1) очередной момент времени, как:
t0 =min {t110, t311, t621, t926}
Для примера рис. 2 t0=t110 .
Таким образом, из начального состояния система переходит в новое состояние в момент времени t110, соответствующее временному условию h1,t9.
В этот момент времени инициатор I1 процесса Z1 перемещается в элементарный оператор (h1,c10, h1,л10) , вычисляя новое состояние объекта O1, а значит, и системы в целом. При этом оказывается выполненным условие h4,Л15 и h7,Л19.. В треке процесса Z4 выполняется оператор состояния h4,с16 и устанавливается логическое условие h4,Л16, а в треке процесса Z7 – h7,с20 и временное условие h7,t20. На рис. 2 соответствующие события отмечены светлыми кружками. Событие по временному условию показано на рис. 6 в виде темного кружка. Так как больше условий не выполняется, то необходимо перейти к новым элементарным операторам в соответствии с треками. В рассматриваемый момент времени следующее активное временное множество имеет вид ![]() . Согласно (1) необходимо перейти к новому моменту времени
. Согласно (1) необходимо перейти к новому моменту времени ![]() . В нашем случае t0=
. В нашем случае t0=![]() . Первым выполняется оператор
. Первым выполняется оператор ![]() , который изменяет состояние объекта O3 и системы в целом, а также формирует новый заказ времени передвижения своего инициатора I3 в момент времени
, который изменяет состояние объекта O3 и системы в целом, а также формирует новый заказ времени передвижения своего инициатора I3 в момент времени ![]() . При этом выполняются логические условия для процессов Z5 и Z8. Инициаторы I5 и I8 вызывают выполнение операторов <h5,c7,h5,л7 > и <h8,c32 ,h8,л32> соответственно. Формируется новое активное временное множество:
. При этом выполняются логические условия для процессов Z5 и Z8. Инициаторы I5 и I8 вызывают выполнение операторов <h5,c7,h5,л7 > и <h8,c32 ,h8,л32> соответственно. Формируется новое активное временное множество: ![]() , наименьшим в котором является
, наименьшим в котором является ![]() . С оператора
. С оператора ![]() и начинается следующий цикл вычислений, и т.д.
и начинается следующий цикл вычислений, и т.д.
На этом примере хорошо иллюстрируется алгоритм продвижения модельного времени и порядок выполнения элементарных операторов в каждом процессе. Сделаем некоторые обобщения.
Выполнение каждого элементарного оператора назовем событием в системе. Событие активное, если оно следует в треке за элементарным оператором, содержащем ht. На рис. 2 условия, содержащие ht , выделены жирным шрифтом. К активным событиям относятся выполнение <h101,c,h101,л>, <h113,c,h113,t>, <h216,c,h216,л> и т.д.
Событие пассивное, если оно следует в треке за элементарным оператором, содержащем hл. На рис. 2 к пассивным событиям относятся выполнение <h111,c,h111,t>, <h92,c,h92,л>, <h174,c,h174,л> и т.д.
Множество событий, происходящих в один и тот же момент модельного времени, назовем классом одновременных событий (КОС). На рис. 2 класс одновременных событий в момент времени ![]() включает события для 1, 4 и 7-го процессов; в момент времени
включает события для 1, 4 и 7-го процессов; в момент времени ![]() КОС составляют события для 3, 5 и 8-го процессов и т.д.
КОС составляют события для 3, 5 и 8-го процессов и т.д.
Рассмотрение КОС примера на рис. 2 показывает, что в каждом КОС содержится активное событие. Введем следующие допущения:
Допущение 1. В каждом КОС содержится одно и только одно активное событие.
Тогда: а) все остальные события в КОС, если они есть, являются пассивными;
б) количество КОС равно мощности объединенного множества времен T.
Допущение 2. Первым событием в любом КОС является активное событие.
Если это так, то оставшиеся пассивные события для определения последовательности своего выполнения требуют знания отношения сцепления. Представим отношение сцепления в КОС в виде направленного графа. На рис. 3 приведен пример некоторого КОС с заданным на нем отношением сцепления.

Рисунок 3. Пример КОС
Здесь: ha - активное событие; hb, hc, hd, he, hf- пассивные события.
Из графа следует, что после ha необходимо выполнить hb либо hc; затем hd, либо he; и наконец hf.
Задание отношения сцепления для каждого КОС является самостоятельной задачей. Однако можно предложить таким образом определять условие выполнения каждого пассивного события, чтобы оно содержало условие выполнения предыдущего события, т.е. содержало описание отношения сцепления с предыдущим событием.
Так, условие выполнения события hd должно содержать выражение, проверяющее выполнение события hb. Если это удается сделать, то алгоритм формирования КОС выглядит следующим образом:
1. Выполняется активное событие.
2. Проверяются условия всех возможных в системе пассивных событий.
3. Если выполняется условие пассивного события, то оно вычисляется. Алгоритм продолжается с п.2.
Важно найти признак, по которому можно определить завершенность КОС.
Теорема А
КОС завершен, если все условия, заданные операторами hл во всех треках, равны 0.
Поскольку КОС содержит одно активное событие и оно выполняется первым, то все остальные события пассивные. Пассивное событие по определению выполняется, если определяющее его условие равно 1. Однако, по предположению, все условия, заданные hл , равны 0. Таким образом, выполнение пассивного события невозможно, а единственное активное событие уже выполнено. Поскольку не выполняется ни один элементарный оператор, состояние системы и параметры условных операторов не могут быть изменены. Состояние системы зафиксировано и не будет изменено вплоть до нового КОС. Что и требовалось доказать.
Теорема Б
Первым событием в КОС является активное событие.
Доказывая теорему А, мы показали, что когда завершен КОС, то все условия в условных операторах системы равны 0, и состояние системы не может быть изменено ни одним пассивным событием. Значит, следующий КОС может начаться только с активного события. Что и требовалось доказать.
Таким образом, наше допущение 2 о начальной функции активного события в КОС доказано строго в теореме Б.
Литература
1. Бусленко Н.П., Калашников В.В., Коваленко И.Н. Лекции по теории сложных систем. - М.: Сов.Радио, 1973. - 438 с.
2. Черненький В.М. Процессно-ориентированная концепция системного моделирования АСУ: диссертация ... доктора технических наук: 05.13.06, М., 2000 - 299 с.ил.
Публикации с ключевыми словами: последовательно-параллельные процессы, имитационный процесс, дискретные системы, отображение параллельных процессов на имитационный
Публикации со словами: последовательно-параллельные процессы, имитационный процесс, дискретные системы, отображение параллельных процессов на имитационный
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



