научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2012
УДК 621.396
МГТУ им. Н.Э. Баумана
В глобальных навигационных спутниковых системах (ГНСС) существуют приложения, в которых решается задача ускоренного поиска в условиях приема слабого сигнала. Для этой цели в некоторых приемниках применяется та или иная схема быстрого поиска, которая основана на реализации алгоритмов быстрой свертки и распараллеливания процесса поиска.
1. Структурная схема обнаружителя сигнала ГНСС
В статье рассматриваем обнаружитель спутниковых радионавигационных сигналов (СРНС) (структурная схема обнаружителя представлена на рис.1), в которой применяется алгоритм согласованной фильтрации в частотной области, базирующийся на методах быстрого преобразования Фурье (БПФ). Этот алгоритм обладает серьезным преимуществом перед корреляционной обработкой: согласованный фильтр инвариантен к задержке сигнала, что позволяет отказаться от переборных процедур поиска сигнала по времени и реализовать параллельный анализ во всех временных элементах разрешения [1]. Это обеспечивает заметное сокращение времени поиска сигнала.

Рис.1. Структурная схема обнаружителя СРНС
Поиск по второму неизвестному параметру – доплеровской частоте Fд –реализуется путем последовательного перебора ряда заранее заданных значений доплеровского сдвига. Для принятия решения о наличии или отсутствии сигнала в каждом элементе разрешения по задержке (канале) τз используем вычислитель решающей статистики (ВРС), реализующий последовательный алгоритм с комбинированной статистикой. В статье [2] был проведен сравнительный анализ статистических характеристик последовательного алгоритма, основанного на критерии Вальда, многоканальной последовательной процедуры с независимыми решениями, алгоритма поиска с зависимыми решениями, последовательного правила Маркуса-Сверлинга и алгоритма с комбинированной решающей статистикой. В условиях приема слабого сигнала оптимальным является последовательный алгоритм с комбинированной статистикой.
2. Последовательный алгоритм поиска с комбинированной статистикой
Принцип построения алгоритма заключается в формировании двух решающих правил и сравнение их с двумя независимыми решающими порогами. Структура каждой из этих статистик, именуемых в дальнейшем соответственно “статистикой обнаружения” и “статистикой необнаружения”, выбирается исходя из конкретных условий решаемой задачи.
Для решения задачи поиска и обнаружения сигнала ГНСС может применяться процедура с комбинированной статистикой, предусматривающая, что проверка гипотезы H1 в каждом канале производится путем сравнения его парциальной статистики Λjс решающим порогом
A1* = m·A1 = m·ln(F1-1),
где m – число каналов (ячеек поиска по задержке), F – вероятность ложной тревоги, A1 – значение верхний порог, которое вычисляется формулой  [3]
[3]
При пересечении порога A*1 гипотеза H1 в данном канале считается принятой независимо от состояния других каналов, т.е. для проверки H1 используется последовательное правило с независимыми решениями. Гипотеза H0 об отсутствии сигналов проверяется на основании сравнения с вальдовским нижним порогом B1 ( ) статистики безусловного отношения правдоподобия, вычисленной для тех каналов, где не был превышен верхний порог. «Статистика необнаружения» формируется следующим образом:
) статистики безусловного отношения правдоподобия, вычисленной для тех каналов, где не был превышен верхний порог. «Статистика необнаружения» формируется следующим образом:
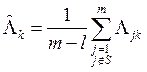 . (1)
. (1)
Здесь S – множество индексов каналов, в которых на k-ом шаге Λj≥ A1, l - число таких каналов.
В задачах обнаружения сигналов ГНСС только в одной ячейке по времени задержки может находиться корреляционный пик, превышающий верхний порог статистики, соответствующий принятию решения о наличии сигнала того или иного спутника на входе приемника поэтому в формуле (1) l = 1.
Рассмотренное правило может быть записано в виде
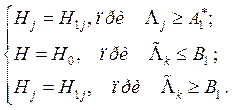
3. Начальные условия для моделирования
На вход обнаружителя подается сигнал с выхода аналогово-цифрового преобразователя (АЦП) на промежуточной частоте (ПЧ). В качестве начальных условий принимаем, что сигнал является детерминированным на фоне узкополосного гауссовского шума с известным СКО (σ = 1), немодулированным информационным сообщением. Логарифм порциальной решающей статистики такого сигнала имеет следующий вид:
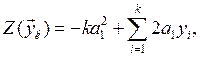
где yk – выходные отсчеты с коррелятора, a1 – ожидаемое значение отсчета с коррелятора
Вероятность правильного обнаружения D = 0.5; вероятность пропуска сигнала F = 10-4.
4. Результаты моделирования блока обнаружителя
4.1. Зависимость средней длительности процедуры при обнаружении и правильном необнаружении сигнала от числа каналов при отношении с/ш (ОСШ) равным 0дБ
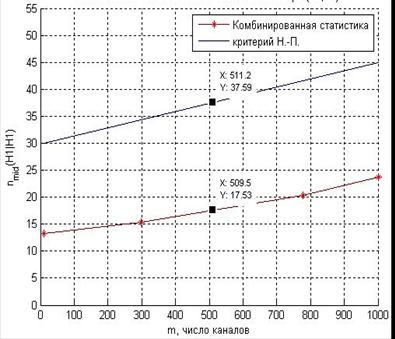
Средняя длительность последовательной процедуры линейно зависит от увеличения числа каналов. На рис.2 представлена зависимость числа шагов поиска от числа каналов при правильном обнаружении сигнала. По значениям, выделенным маркерами, видно, что, если сигнал присутствует в канале, то обнаружитель, реализующий последовательное правило поиска с комбинированной статистикой, примет решение о его наличии в два раза быстрее, чем при использовании классического критерия Неймана-Пирсона, если сигнал отсутствует – в четыре раза быстрее.
а
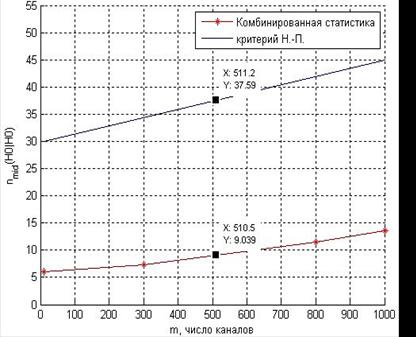
б
Рис. 2. Зависимость числа шагов поиска сигнала от числа каналов:
а – при правильном обнаружении; б – при правильном необнаружении
4.2. Характеристики обнаружения
В одноканальном обнаружителе (рис. 3) вероятность правильного приема D для комбинированной статистики при различных значениях ОСШ выше, чем для критерия Неймана-Пирсона. В многоканальном обнаружителе характеристики обнаружения двух алгоритмов близки по значениям друг другу.
а |
б |
Рис. 3. Характеристики обнаружения сигнала при различном числе каналов: | |
5. Выводы
Было установлено:
− разработана модель блока обнаружителя сигнала ГНСС в программном пакете MATLAB, которая позволят проводить анализ и исследования различных алгоритмов поиска;
− алгоритм последовательного поиска с комбинированной статистикой имеет аналогичные характеристики обнаружения, что и алгоритм с решающим правилом Неймана-Пирсона;
− при фиксированных характеристиках обнаружения рассмотренный алгоритм позволяет снизить среднее время обнаружения сигнала ГНСС при низком уровне ОСШ (0 дБ) в среднем в два раза при наличии сигнала, в четыре раза – при отсутствии сигнала.
Список использованных источников
1. Информационные технологии в радиотехнических системах: Учебное пособие / В.А. Васин, И.Б. Власов, Ю.М. Егоров и др.; Под ред. И.Б. Федорова. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2011.
2. И.Б. Власов, Я.В. Мыкольников. Ускоренный поиск в частотной области с использование последовательных (вальдовских) правил. М.: МГТУ им. Н.Э. Баумана, 2007.
3. Вальд А. Последовательный анализ: Пер. с англ./Под ред. Б.А. Севастьянова. – М.: Физматгиз, 1960.
4. Розанов Б.А., Соловьев Г.Н. К оценке эффективности многоканального анализа с одновременным принятием решений в каналах. – М.: Радиотехника и электроника.
5. Ширман Я.Д., Манжос В.Н. Теория и техника обработки радиолокационной информации на фоне помех. М.: Радио и Связь, 1981.
Публикации с ключевыми словами: глобальная навигационная спутниковая система, блок обнаружения, последовательный алгоритм поиска
Публикации со словами: глобальная навигационная спутниковая система, блок обнаружения, последовательный алгоритм поиска
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||





