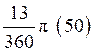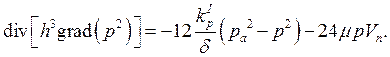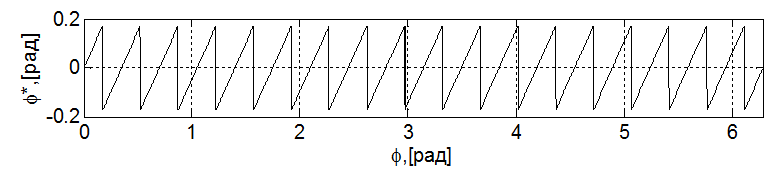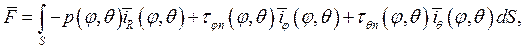научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
DOI: 10.7463/1211.0286475
УДК 004.942; 519.632;533; 621.822.174
МГТУ им. Н.Э. Баумана
1. Введение
Аэростатические опоры используются в прецизионных станках металлообработки, приборостроении, измерительной и турбокомпрессорной технике независимо или в сочетании с аэродинамическими опорами во время пуска или останова [1].
При проектировании и оптимизации аэростатических опор необходимо решать уравнение, описывающие распределение давления воздуха на опорные поверхности подвижных частей [2]
![]()
 (1.1)
(1.1)
где ![]() аэростатический зазор;
аэростатический зазор; ![]() коэффициент динамической вязкости воздуха;
коэффициент динамической вязкости воздуха; ![]() давление воздуха;
давление воздуха; ![]() коэффициент политропы для движения воздуха;
коэффициент политропы для движения воздуха; ![]() сумма векторов касательных скоростей;
сумма векторов касательных скоростей; ![]() разность векторов касательных скоростей;
разность векторов касательных скоростей; ![]() скорость поверхности шпинделя;
скорость поверхности шпинделя; ![]() скорость поверхности корпуса (Рисунок 1);
скорость поверхности корпуса (Рисунок 1); ![]() разность нормальных скоростей;
разность нормальных скоростей; ![]() время.
время.
Уравнение распределения давления является нелинейным дифференциальным уравнением эллиптического типа в частных производных, поиск точного аналитического решения которого остается неразрешимой задачей [3]. Известны различные методы решения уравнения распределения давления: разложение в ряды [2], метод конечных разностей [3], метод конечных элементов, бессточные методы [4]. Как правило, эти методы используются после ряда упрощений. В физической модели часто пренебрегают изменением температуры, сжимаемостью воздуха [2] или скоростями поверхностей. В математической модели часто применяются линеаризация и переход от трехмерной задачи к двух- или одномерной. Также часто встречаются упрощения геометрии: метод линий наддува [5], метод точечных источников [2, 6]. Решение уравнения - это ключевой этап расчета аэростатических опор, который позволяет вычислять опорные реакции для определения статических и динамических характеристик, анализа устойчивости или переходных процессов. Использование указанных методов решения уравнения распределения давления связано или с чрезмерными упрощениями или с громоздким математическим аппаратом. Расчеты аэростатических опор со сферическими или коническими опорными поверхностями существенно осложняется связью силовых характеристик в осевом и радиальных направлениях.
Для сокращения количества интегрирований уравнения предложена сегментная модель, позволившая сравнительно просто определить опорные реакции на основании предварительной серии вычислений поля давления для малого сегмента опорной поверхности. Предложенная модель опробована на сферических аэростатических опорах с пористыми ограничителями наддува для низкоскоростного шпинделя прецизионного станка МК 6524 разрабатываемого в ОАО "Ресурс точности". Предполагается возможность использования данной модели для аэростатических опор другой формы или иными ограничителями напора.
2. Особенности сферических аэростатических опор
Исследованный шпиндельный узел состоит из шпинделя 1, корпуса 2 и пористых вставок 3 для дросселирования воздуха (Рисунок 1).
Рисунок 1. Разрез шпиндельного узла
Преимуществами такой компоновки является то, что всего две опорные поверхности воспринимают радиальные, осевые и перекашивающие ось нагрузки, а также простота контроля относительного положения опорных поверхностей. Предполагается, что за счет этих преимуществ опоры можно будет изготавливать с меньшим аэростатическим зазором, а значит получить большую жесткость.
Одним из основных недостатков является сложность расчета силовых характеристик шпинделя на таких опорах. В отличие от наиболее распространенных цилиндрических опор, состояние воздушного слоя между двумя сферами зависит от радиальных, осевых и перекашивающих смещений и скоростей шпинделя. Нельзя отдельно исследовать отклик шпинделя на силовые воздействия в каждом направлении. Описание статических и динамических характеристик требует многократного интегрирования уравнение распределение давления. В данной статье описан один из вариантов построения упрощенной модели, позволивший преодолеть указанные расчетные трудности.
Геометрия опор
Поскольку обе сферические поверхности шпинделя одинаковые, то на первом этапе исследования основной задачей становится определение силовых характеристик одной сферической опоры. Её чертеж представлен на рисунке 2, параметры указаны в таблице 1.

Рисунок 2. Размеры основных конструктивных элементов
Таблица 1
Параметры шпиндельного узла.
Номинальный зазор |
| м | 10e-6 |
Радиус сферы |
| м | 0,11 |
Количество вставок |
| шт. | 18 |
Проницаемость вставок |
| м | 9,6e-15 |
Толщина вставок в центре |
| м | 6e-3 |
Радиус вставки |
| м | 11e-3 |
Угловой размер |
| рад (град) |
|
Угловой размер |
| рад (град) |
|
Угловое положение вставки |
| рад (град) |
|
Давление подачи (изб.) |
| Па |
|
|
|
|
|
Для дальнейшего описания, введены декартовы и сферические системы координат: глобальные, связанные с некоторой первой вставкой ![]() и
и ![]() (Рисунок 3 - а), а также локальные, связанные с остальными вставками
(Рисунок 3 - а), а также локальные, связанные с остальными вставками ![]() (Рисунок 3 - б). Также введена дополнительная локальная декартова систем координат, связанная с первой вставкой
(Рисунок 3 - б). Также введена дополнительная локальная декартова систем координат, связанная с первой вставкой ![]() (Рисунок 3 - в).
(Рисунок 3 - в).

Рисунок 3. Использованные системы координат: а - глобальные, б - локальные, связанные с центром ![]() - ной вставки
- ной вставки
Связь глобальных декартовых ![]() и глобальных сферических координат
и глобальных сферических координат ![]() осуществлялась через следующие уравнения (Рисунок 3-а)
осуществлялась через следующие уравнения (Рисунок 3-а)
![]()

Локальные координаты ![]() связанны с глобальными
связанны с глобальными ![]() с помощью матрицы поворота
с помощью матрицы поворота ![]() (Рисунок 3-б)
(Рисунок 3-б)
![]()
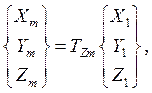
где  матрица поворота относительно оси
матрица поворота относительно оси ![]() на угол
на угол ![]() .
.
Локальные координаты ![]() связанны с глобальными
связанны с глобальными ![]() с помощью матрицы поворота
с помощью матрицы поворота ![]() (Рисунок 3-в)
(Рисунок 3-в)
![]()

где  - матрица поворота относительно оси
- матрица поворота относительно оси ![]() на угол
на угол ![]() .
.
3. Упрощенная сегментная модель
Физические допущения
Как и во многих других работах [2,3,4], движение воздуха считалось изотермическим и стационарным, а сопротивление пористых ограничителей напора, согласно уравнению Дарси. Величина зазора пренебрежимо малой по сравнению с радиусом сфер. Кроме того были сделаны два дополнительных допущения физического характера. Опорная поверхность была разделена на симметричные сегменты, центр каждого совпадал с центром некоторой вставки (эта точка считалась полюсом сегмента). Во-первых, количество сегментов считалось большим. В пределах каждого сегмента зазор и нормальная скорость поверхности шпинделя считались постоянными, а распределения давлений в соседних сегментах отличающимися не сильно. Во-вторых, не учитывалось влияние касательных скоростей поверхности шпинделя![]() и
и ![]() , сумма и разность которых в уравнении умножаются на малую величину зазора или его производной. Оправдание этого утверждения является низкая скорость вращения шпинделя, создаваемого для точения цветных металлов. Следствием физических допущений стали следующие математические упрощения:
, сумма и разность которых в уравнении умножаются на малую величину зазора или его производной. Оправдание этого утверждения является низкая скорость вращения шпинделя, создаваемого для точения цветных металлов. Следствием физических допущений стали следующие математические упрощения:
скорость поверхности шпинделя постоянна и равна нормальной скорости, вычисленной в полюсе области ![]() ;
;
зазор в пределах одной области постоянен и равен зазору, вычисленному в полюсе области;
на смежных границах областей для решения уравнения распределения давления задается граничное условие симметрии (условие Неймана).
На основании принятых упрощений уравнение распределения давления после упрощения приняло вид
где ![]() - толщина пористой вставки,
- толщина пористой вставки, 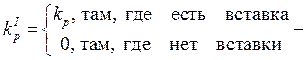 коэффициент проницаемости материала корпуса;
коэффициент проницаемости материала корпуса; ![]() коэффициент проницаемости материала пористой вставки. Таким образом, за счет приема, предложенного Заболоцким Н.Д.[7], можно одним уравнением описать состояние газового слоя в области, где есть пористая вставка и там, где ее нет.
коэффициент проницаемости материала пористой вставки. Таким образом, за счет приема, предложенного Заболоцким Н.Д.[7], можно одним уравнением описать состояние газового слоя в области, где есть пористая вставка и там, где ее нет.
После принятых допущений распределение давление в каждом сегменте можно считать зависящим не от пяти пространственных координат и шести скоростей шпинделя, а только от нормального смещения ![]() и нормальной скорости
и нормальной скорости ![]() в его полюсе сегмента. При постоянном давлении подачи
в его полюсе сегмента. При постоянном давлении подачи ![]() , нормальное смещение
, нормальное смещение ![]() и нормальная скорость
и нормальная скорость ![]() , являются фазовыми переменными сегмента, а множество значений, которые они могут принимать образуют фазовое пространство сегмента.
, являются фазовыми переменными сегмента, а множество значений, которые они могут принимать образуют фазовое пространство сегмента.
По распределению давления можно вычислить равнодействующие опорные реакции, которые также зависят только от нормального смещения и нормальной скорости. Воздушный слой в каждом сегменте можно считать нелинейным упруго-вязким элементом, опорные реакции в котором определяются смещением и скоростью (Рисунок 4).

Рисунок 4. Опорные реакции, приложенные к расчетному сегменту
Для определения силовых характеристик упругих элементов была проведена серия предварительных расчетов в пространстве ![]() -
- ![]() , на основании которой опорные реакции определялись интерполяцией. Таким образом, представлена последовательность определения опорных реакций, без решения уравнения распределения давления для каждого состояния шпинделя
, на основании которой опорные реакции определялись интерполяцией. Таким образом, представлена последовательность определения опорных реакций, без решения уравнения распределения давления для каждого состояния шпинделя
-вычисление нормального смещения ![]() и нормальной скорости
и нормальной скорости ![]() в полюсе каждой области по смещениям и скоростям шпинделя
в полюсе каждой области по смещениям и скоростям шпинделя
-определение опорных реакций в каждой области по интерполяционной зависимости
-нахождение суммарных опорных реакций, приложенных к шпинделю.
Расчет распределения давления
Уравнение распределения давления было проинтегрировано численно методом конечных элементов в программе MATLAB для различных значений нормального смещения ![]() и нормальной силы
и нормальной силы ![]() . Решение проводилось в нелинейной постановке без дополнительных упрощений. Для решения использовались треугольные трехузловые элементы. Сходимость решения при сгущении сетки проверена. Нелинейное решение проводилось методом Ньютона с пересчетом "матрицы жесткости". На рисунке 5 представлена сетка конечных элементов, использованная для решения.
. Решение проводилось в нелинейной постановке без дополнительных упрощений. Для решения использовались треугольные трехузловые элементы. Сходимость решения при сгущении сетки проверена. Нелинейное решение проводилось методом Ньютона с пересчетом "матрицы жесткости". На рисунке 5 представлена сетка конечных элементов, использованная для решения.
Рисунок 5. Сетка конечных элементов для расчета давления в одном сегменте
В уравнение входит переменный коэффициент проницаемости материала корпуса ![]() и переменная толщина вставки
и переменная толщина вставки ![]() . Для их описания, использовалась локальная декартова система координат
. Для их описания, использовалась локальная декартова система координат ![]() (Рисунок 3-в). После этого вводилось расстояние от оси
(Рисунок 3-в). После этого вводилось расстояние от оси ![]() первой вставки:
первой вставки:
![]() .
.
Тогда выражение для коэффициента проницаемости поверхности корпуса примет вид:
Т.к. одна стенка вставки плоская, а другая сферическая, то толщина вставки не постоянна и зависит от расстояния до оси вставки ![]() (Рисунок 6). Зависимость толщины вставки от сферических координат можно выразить так
(Рисунок 6). Зависимость толщины вставки от сферических координат можно выразить так

Рисунок 6. Вычисление переменной толщины вставки ![]()
Формулы и справедливы только для первой вставки. Чтобы они описывали переменную толщину и проницаемость других вставок, в них надо заменить угол ![]() на угол
на угол ![]() , отсчитываемый от центра ближайшей вставки. Угол
, отсчитываемый от центра ближайшей вставки. Угол ![]() можно вычислить по формуле
можно вычислить по формуле
где ![]() остаток от деления
остаток от деления ![]() на
на ![]() , график этой функции представлен на рисунке 7.
, график этой функции представлен на рисунке 7.
Рисунок 7. Вид функции 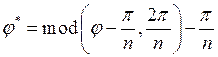 .
.
После преобразований уравнение в сферической системе координат приняло вид
где ![]() - нормальное смещение в полюсе сегмента относительно равномерного зазора,
- нормальное смещение в полюсе сегмента относительно равномерного зазора, ![]() номинальный зазор,
номинальный зазор,  переменный коэффициент. В уравнении отсутствуют производные давления по радиусу, т.к. радиальная скорость воздуха пренебрегается по сравнению с касательными скоростями. Для работы с уравнением удобно использовать безразмерную функцию давления
переменный коэффициент. В уравнении отсутствуют производные давления по радиусу, т.к. радиальная скорость воздуха пренебрегается по сравнению с касательными скоростями. Для работы с уравнением удобно использовать безразмерную функцию давления
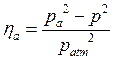 .
.
После расчета значений безразмерной функции давления ![]() само давление можно получить по обратной зависимости
само давление можно получить по обратной зависимости
![]()
Уравнение после подстановки функции давления ![]() приняло вид
приняло вид
Коэффициенты уравнения вычислялись численно в узлах сетки. На рисунке 8 представлена зависимость коэффициента ![]() от сферических координат.
от сферических координат.
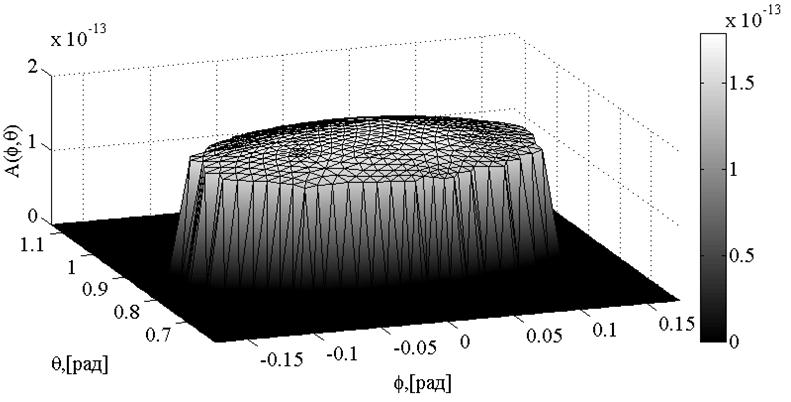
Рисунок 8. Зависимость коэффициента ![]() от сферических координат
от сферических координат ![]()
Уравнение можно решить численно для различных сочетаний нормального смещения полюса сегмента относительно нейтрального положения ![]() и нормальной скорости
и нормальной скорости ![]() . На рисунке 9 показано распределение давления в расчетной области для случая
. На рисунке 9 показано распределение давления в расчетной области для случая ![]() и
и ![]() . Это случай соответствует невозмущенному состоянию шпинделю в нейтральном положении с нулевой скоростью.
. Это случай соответствует невозмущенному состоянию шпинделю в нейтральном положении с нулевой скоростью.

Рисунок 9. Распределение давления ![]() на расчетном сегменте при
на расчетном сегменте при ![]() и
и ![]()
Уравнение при нулевой нормальной скорости сегмента ![]() становиться линейным, при этом процесс решения в нелинейной постановке сходился за одну итерацию. При других сочетаниях смещения сегмента
становиться линейным, при этом процесс решения в нелинейной постановке сходился за одну итерацию. При других сочетаниях смещения сегмента ![]() и нормальной скорости смещения полюса
и нормальной скорости смещения полюса ![]() также проводилось решение в нелинейной постановке, при этом проверялась сходимость. В фазовом пространстве сегмента выявлены две области, в которых численное решение расходилось или давало комплексный результат. На рисунке 10 показаны две области расхождения А и Б. Их наличие объясняется тем, что при сокращении зазора, увеличивается влияние скорости на распределение давления в сегменте. Также показаны геометрические пределы перемещения до возникновения контакта опорных поверхностей. Смещение
также проводилось решение в нелинейной постановке, при этом проверялась сходимость. В фазовом пространстве сегмента выявлены две области, в которых численное решение расходилось или давало комплексный результат. На рисунке 10 показаны две области расхождения А и Б. Их наличие объясняется тем, что при сокращении зазора, увеличивается влияние скорости на распределение давления в сегменте. Также показаны геометрические пределы перемещения до возникновения контакта опорных поверхностей. Смещение ![]() не может быть больше величины номинального зазора. В отрицательном направление смещение может произойти на большую величину, чем величина зазора.
не может быть больше величины номинального зазора. В отрицательном направление смещение может произойти на большую величину, чем величина зазора.

Рисунок 10. Области расхождения решений в фазовом пространстве сегмента
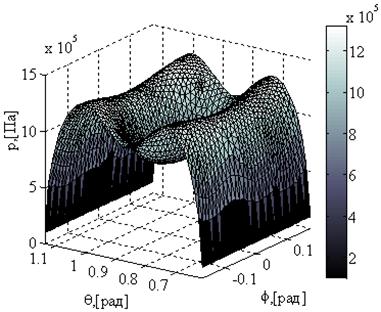
На рисунке 11- а и б представлены эпюры распределения давления вблизи области А и области Б, соответственно.

а) б)
Рисунок 11. Распределения давлений ![]() в расчетном сегменте вблизи областей расхождения решений. а – при быстром сжатии зазора, б – при быстром расширении
в расчетном сегменте вблизи областей расхождения решений. а – при быстром сжатии зазора, б – при быстром расширении
При положительном смещении ![]() и значительной положительной скорости
и значительной положительной скорости ![]() расчетное давление на опорном сегменте может превысить давление подачи, что соответствует движению воздуха через ограничитель наддува в противоположенном направлении (Рисунок 11-а). Такое состояние сегмента не может быть стационарным, поскольку очень скоро зазор перекроется. Вблизи области А на точность описания распределения давления может сказаться пренебрежения производной давления по времени в уравнении и скорости заполнения пор в материале вставок.
расчетное давление на опорном сегменте может превысить давление подачи, что соответствует движению воздуха через ограничитель наддува в противоположенном направлении (Рисунок 11-а). Такое состояние сегмента не может быть стационарным, поскольку очень скоро зазор перекроется. Вблизи области А на точность описания распределения давления может сказаться пренебрежения производной давления по времени в уравнении и скорости заполнения пор в материале вставок.
При положительном смещении ![]() и отрицательной скорости
и отрицательной скорости ![]() расчетное давление в некоторых точках зазора уменьшается ниже атмосферного, что приводит к большим градиентам давления или комплексному и не физичному результату, соответствующему комплексному значения давления (Рисунок 11-б). Вблизи областей А и Б могут проявиться пренебреженные ранее физические эффекты: сплошности, изотермичности и стационарности движения воздуха [2], а также различные математические трудности. Поэтому расчетный диапазон был скорректирован и из него отброшены области А и Б, а также прилегающие к ним точки. Для упрощения криволинейные границы выбраны симметричными, для областей А и Б, при этом сохранены все точки с нулевой скоростью, чтобы повысить точность статических характеристик. Это возможно за счет того, что при нулевой скорости
расчетное давление в некоторых точках зазора уменьшается ниже атмосферного, что приводит к большим градиентам давления или комплексному и не физичному результату, соответствующему комплексному значения давления (Рисунок 11-б). Вблизи областей А и Б могут проявиться пренебреженные ранее физические эффекты: сплошности, изотермичности и стационарности движения воздуха [2], а также различные математические трудности. Поэтому расчетный диапазон был скорректирован и из него отброшены области А и Б, а также прилегающие к ним точки. Для упрощения криволинейные границы выбраны симметричными, для областей А и Б, при этом сохранены все точки с нулевой скоростью, чтобы повысить точность статических характеристик. Это возможно за счет того, что при нулевой скорости ![]() уравнение становится линейным относительно функции давления
уравнение становится линейным относительно функции давления ![]() , а процесс нелинейного решения сходится за одну итерацию. На рисунке 12 черным цветом показаны точки, выбранные для расчета силовых характеристик сегмента, серым - отброшенные точки.
, а процесс нелинейного решения сходится за одну итерацию. На рисунке 12 черным цветом показаны точки, выбранные для расчета силовых характеристик сегмента, серым - отброшенные точки.

Рисунок 12. Точки фазового пространства, взятые для расчета
При дальнейшем использовании сегментной модели желательно следить за тем, чтобы фазовое состояние всех сегментов не выходило за пределы расчетной области. Следует отметить, что подбор границ областей сходимости решения в двухмерном фазовом пространстве ![]() является сложной задачей, но, несомненно, более простой, чем подбор границ сходимости в многомерном фазовом пространстве перемещений и скоростей одной полусферы при расчете давления во всей опорной поверхности.
является сложной задачей, но, несомненно, более простой, чем подбор границ сходимости в многомерном фазовом пространстве перемещений и скоростей одной полусферы при расчете давления во всей опорной поверхности.
Определение опорных реакций в одном сегменте
При найденном распределении давления ![]() на поверхность сегмента вектор равнодействующей опорной реакции
на поверхность сегмента вектор равнодействующей опорной реакции ![]() были определены интегрированием давления и касательных напряжений, приложенных к нему (рисунок 5)
были определены интегрированием давления и касательных напряжений, приложенных к нему (рисунок 5)
где![]() опорные реакции, приложенные к сегменту в локальной системе координат,
опорные реакции, приложенные к сегменту в локальной системе координат, ![]() площадь отдельного сегмента
площадь отдельного сегмента ![]() касательные напряжение вязкого трения,
касательные напряжение вязкого трения,![]() орты сферической системы координат (Рисунок 3-а). Орты
орты сферической системы координат (Рисунок 3-а). Орты ![]() выражены следующим зависимостям
выражены следующим зависимостям
Касательное напряжение вычислялось по формулам [2]
С учетом и силы, действующие на сегмент, были выражены следующим образом
где ![]() - границы расчетного сегмента. Проекция реакции
- границы расчетного сегмента. Проекция реакции ![]() равна нулю из симметрии задачи. Следует отметить, что рассматривать отдельно одну полусферическую опору, то на свободную поверхность действует атмосферное давление воздуха. Для получения равнодействующей силы воздушного давления на всю поверхность опоры в уравнении нужно подставить вместо абсолютного давления
равна нулю из симметрии задачи. Следует отметить, что рассматривать отдельно одну полусферическую опору, то на свободную поверхность действует атмосферное давление воздуха. Для получения равнодействующей силы воздушного давления на всю поверхность опоры в уравнении нужно подставить вместо абсолютного давления ![]() , избыточное давление
, избыточное давление ![]() . Но у шпинделя две одинаковые направленные в противоположенные стороны сферические поверхности (Рисунок 1). Подстановка избыточного давления
. Но у шпинделя две одинаковые направленные в противоположенные стороны сферические поверхности (Рисунок 1). Подстановка избыточного давления ![]() в уравнение не изменит суммарной воздушной реакции. Интегрирование выражений проводилось численно по результатам распределения давления, вычисленного в узлах сетки конечных элементов. После расчета опорных реакций в ряде точек фазового пространства сегмента, были выбраны интерполяционные зависимости для
в уравнение не изменит суммарной воздушной реакции. Интегрирование выражений проводилось численно по результатам распределения давления, вычисленного в узлах сетки конечных элементов. После расчета опорных реакций в ряде точек фазового пространства сегмента, были выбраны интерполяционные зависимости для ![]() и
и ![]() в виде полиномов:
в виде полиномов:
Коэффициенты аппроксимации ![]() определялись числено из условия минимума среднеквадратичной погрешности в расчетных точках фазового пространства.
определялись числено из условия минимума среднеквадратичной погрешности в расчетных точках фазового пространства.
На рисунке 13 сравниваются исходные и аппроксимирующие зависимости осевой и радиальной опорных реакций. Средняя квадратичная погрешность аппроксимации составила 3,343 Н для радиальной силы ![]() и 2,671 Н для осевой силы
и 2,671 Н для осевой силы ![]() .
.
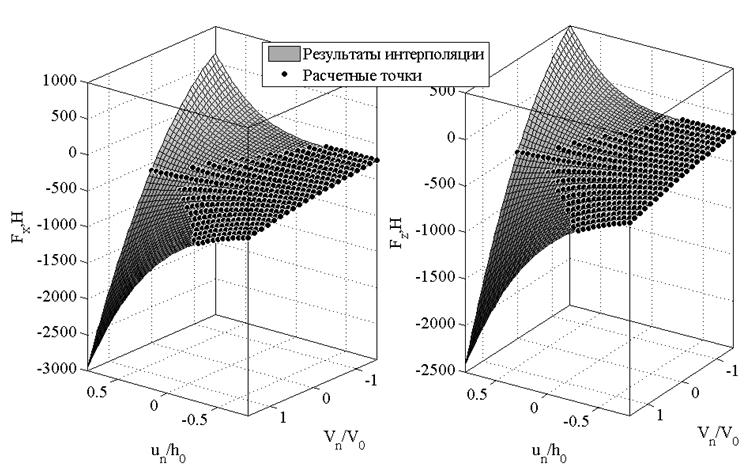
а) б)
Рисунок 13. Результаты аппроксимации силовых характеристик ![]() и
и ![]()
Зависимости проекций опорных реакций сегмента ![]() и
и ![]() оказались практически пропорциональны между собой
оказались практически пропорциональны между собой
![]() .
.
Максимальное отличие от пропорциональности составляет 0,514%. Это означает, что их можно заменить равнодействующей силой, приложенной к расчетному сегменту в точке с углом ![]() , фактически, в центре вставки (Рисунок 14).
, фактически, в центре вставки (Рисунок 14).
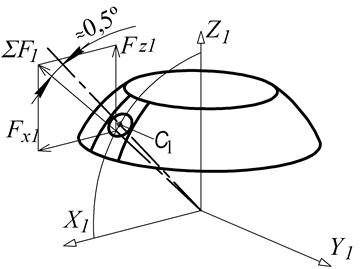
Рисунок 14. Суммарная сила, приложенная к расчетному сегменту
При другой геометрии опорных поверхностей линия действия суммарной силы ![]() может пройти дальше от центра вставки, поэтому нельзя с самого начала считать, что опорная реакция отдельного сегмента приложена именно в центре вставки и направлена вдоль радиуса.
может пройти дальше от центра вставки, поэтому нельзя с самого начала считать, что опорная реакция отдельного сегмента приложена именно в центре вставки и направлена вдоль радиуса.
Определение суммарных опорных реакций
Вычисление равнодействующих сил давления на всю аэростатическую поверхность проводилось векторным суммированием реакций в отдельных сегментах.
Последовательность вычисления опорных реакций можно представить в следующем виде
Задание вектора смещения ![]() и вектора скорости
и вектора скорости ![]() центра сферы шпинделя
центра сферы шпинделя
![]()
2. Вычисление нормального смещения ![]() и нормальной скорости
и нормальной скорости ![]() полюса каждого сегмента. При этом для сферических поверхностей нет необходимости учитывать углы поворота шпинделя вокруг центра сферы, потому что они не влияют на величину нормального смещения поверхности. Нормальное смещение
полюса каждого сегмента. При этом для сферических поверхностей нет необходимости учитывать углы поворота шпинделя вокруг центра сферы, потому что они не влияют на величину нормального смещения поверхности. Нормальное смещение ![]() и нормальная скорость
и нормальная скорость ![]() зависят от вектора смещения
зависят от вектора смещения ![]() и вектора скорости
и вектора скорости ![]() центра сферы, а также от положения полюса сегмента на сфере
центра сферы, а также от положения полюса сегмента на сфере![]() .
.
![]()
![]() .
.
3. Вычисление опорных реакций отдельных сегментов ![]() в локальных системах координат
в локальных системах координат ![]() по аппроксимирующим зависимостям
по аппроксимирующим зависимостям
4. Перевод реакций отдельных сегментов в глобальную декартову систему координат ![]() и их суммирование
и их суммирование

где, 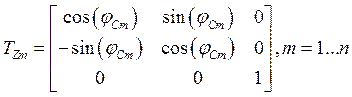 - матрица перехода от
- матрица перехода от ![]() к
к ![]() .
.
Таким образом, на основании двух дополнительных допущений можно определенить опорные реакции шпинделя на сферических аэростатических подшипниках.
4. Верификация модели.
Источниками погрешности являются ошибки численного счета и аппроксимации, а также различные физические допущения. С математическими погрешностями можно бороться в рамках предложенной модели, сгущая сетку конечных элементов или увеличивая число слагаемых в аппроксимирующих зависимостях. Физические допущения о том, что процесс движения является сплошным, изотермически и стационарным являются типичными для моделирования аэростатических опор и достаточно трудоемки для проверки. Наибольший интерес для проверки представляют дополнительные физические допущения и их следствия.
Предполагалось, что зазор в пределах одного сегмента постоянен и равен зазору в центре расчетного сегмента, а на стыках сегментов можно задать граничное условие симметрии. Это допущение существенно исказило эпюру распределения давления в одном сегменте, но не его равнодействующую. Чтобы в этом убедиться, была проведена серия расчетов статических силовых характеристик одной полусферы с разным количеством расчетных сегментов. Количество вставок на одной полусфере равно восемнадцати. Поэтому количество сегментов можно было взять 18, 9, 6, 3 и 2 (Рисунок 15).

Рисунок 15. Различные варианты разбиения на сегменты
Для каждого случая были получены суммарные силовые характеристики одной сферической опоры в осевом и двух радиальных направлениях. Характеристики выглядят непривычно идущими сверху вниз, потому что это не внешняя сила, а опорная реакция, приложенная к шпинделю.
На рисунке 16 сравниваются силовые характеристики в радиальном направлении, вдоль оси ![]()
![]() , полученные для всей сферической опоры при различном количестве сегментов
, полученные для всей сферической опоры при различном количестве сегментов ![]() в расчетной модели. Заметная несимметричность характеристики при
в расчетной модели. Заметная несимметричность характеристики при ![]() объясняется несимметричным расположением сегментов при
объясняется несимметричным расположением сегментов при ![]() .
.

Рисунок 16. Силовые характеристики в радиальном направлении, вдоль оси ![]() для разного количества сегментов
для разного количества сегментов ![]()
На рисунке 17 сравниваются силовые характеристики в радиальном направлении, вдоль оси ![]()
![]() , полученные для всей сферической опоры при различном количестве сегментов
, полученные для всей сферической опоры при различном количестве сегментов ![]() в расчетной модели. При
в расчетной модели. При ![]() сила в радиальном направлении
сила в радиальном направлении ![]() тождественно равна нулю. Это объясняется тем, что при
тождественно равна нулю. Это объясняется тем, что при ![]() смещение шпинделя в направлении
смещение шпинделя в направлении ![]() не вызывает нормальных смещений полюсов сегментов
не вызывает нормальных смещений полюсов сегментов ![]() , сегменты "не работают".
, сегменты "не работают".
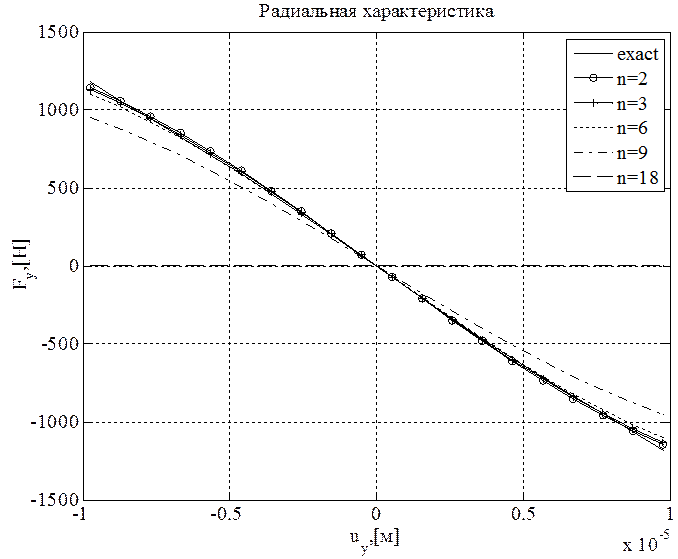
Рисунок 17. Силовые характеристики в радиальном направлении, вдоль оси ![]() для разного количества сегментов
для разного количества сегментов ![]()
На рисунке 18 сравниваются силовые характеристики в осевом направлении ![]() , полученные для всей сферической опоры при различном количестве сегментов
, полученные для всей сферической опоры при различном количестве сегментов ![]() в расчетной модели.
в расчетной модели.
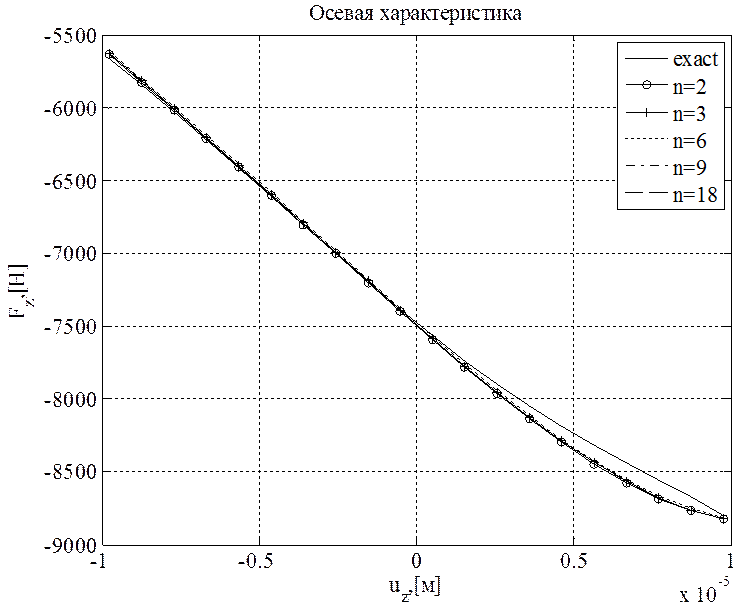
Рисунок 18. Силовые характеристики в радиальном направлении, вдоль оси ![]() для разного количества сегментов
для разного количества сегментов ![]()
Во всех случаях решение сравнивается с более точным, полученным для решения уравнения распределения давления при нулевой скорости поверхности. Уравнение стало линейным относительно функции давления ![]() и приняло вид
и приняло вид
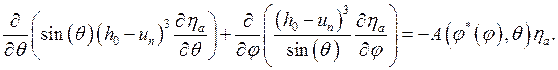
При этом нормальные смещения точек опорной поверхности шпинделя ![]() вычислялось по формуле
вычислялось по формуле
Как видно из смещение центра сферы шпинделя ![]() вызывает различные нормальные смещения точек опорной поверхности
вызывает различные нормальные смещения точек опорной поверхности ![]() . На рисунке 19, в качестве примера, показана зависимость нормального смещения от сферических координат
. На рисунке 19, в качестве примера, показана зависимость нормального смещения от сферических координат ![]() в расчетной области при смещении центра шпинделя на вектор
в расчетной области при смещении центра шпинделя на вектор ![]() .
.
Рисунок 19. Пример зависимости нормального смещения ![]() от сферических координат
от сферических координат ![]()
На рисунке 20 показана зависимость переменного коэффициента ![]() от сферических координат
от сферических координат ![]() в расчетной области.
в расчетной области.
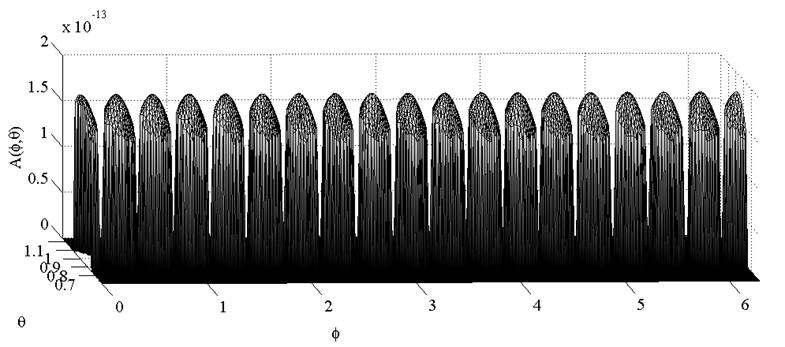
Рисунок 20. Зависимость коэффициента ![]() от сферических координат
от сферических координат ![]()
Решение также проводилось тем же самым математическим аппаратом. Использовался метод конечных элементов в программе Matlab с учащенной для точности сеткой, представленной на рисунке 21.
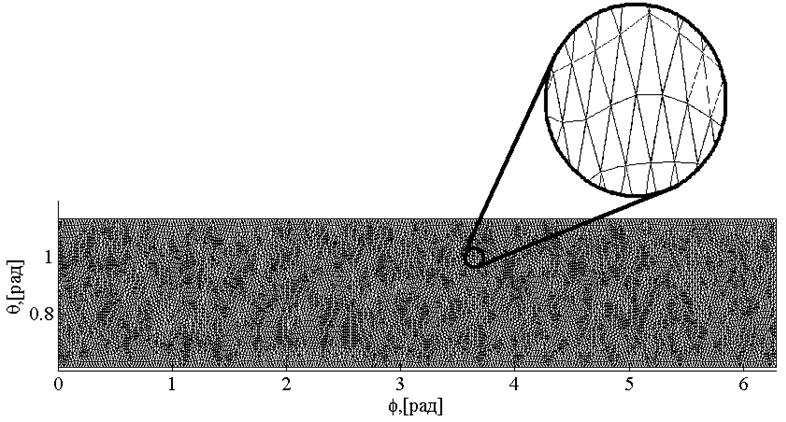
Рисунок 21. Сетка конечных элементов для проверочного решения
На внешних границах было взято граничное условие в виде Дирихле: ![]() , На симметрично расположенной грани разреза было принято граничное условие симметрии:
, На симметрично расположенной грани разреза было принято граничное условие симметрии:  . Опорные реакции определялись по формулам , где областью интегрирования была вся поверхность полусферы
. Опорные реакции определялись по формулам , где областью интегрирования была вся поверхность полусферы ![]() . Так как решения проводились одним и тем же математическим аппаратом, то сопоставление решений позволяет оценить влияние физических допущений, определяющих различие моделей: независимость сегментов и постоянство зазора в сегменте.
. Так как решения проводились одним и тем же математическим аппаратом, то сопоставление решений позволяет оценить влияние физических допущений, определяющих различие моделей: независимость сегментов и постоянство зазора в сегменте.
На рисунке 22 показан пример распределения давления![]() , полученного для того же смещения центра сферы
, полученного для того же смещения центра сферы ![]() , для которого было показано распределение нормального смещения (Рисунок 19).
, для которого было показано распределение нормального смещения (Рисунок 19).

Рисунок 22. Пример распределения давления ![]() , полученного для случая
, полученного для случая ![]()
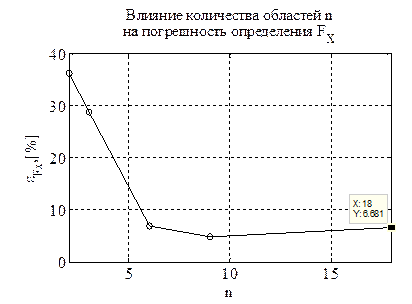
На рисунке 23 представлены зависимости максимальных погрешностей силовых характеристик от точного решения, а в таблице 2 указанны их значения.
а)

б)

в)
Рисунок 23. Погрешность определения силовых характеристик в зависимости от количества сегментов ![]() : а) -
: а) - ![]() ; б) -
; б) -![]() ; в) -
; в) -![]()
Таблица 2.
Погрешности определения силовых характеристик в зависимости от количества сегментов
|
|
|
|
|
|
| 36,28 | 28,73 | 6,852 | 4,883 | 6,681 |
| 100 | 19,17 | 6,56 | 5,102 | 6,903 |
| 1,487 | 1,505 | 1,38 | 1,492 | 1,56 |
Отличие силовых характеристик, полученных по сегментной модели от точного решения, объясняется, прежде всего, дополнительными допущениями, в основе сегментной модели: независимостью полей давления соседних сегментов и постоянством зазора в пределах одного сегмента. При осевом перемещении шпинделя условия симметрии для соседних сегментов выполняются абсолютно точно, поэтому средняя погрешность ![]() 1,6% для осевого перемещения является следствием второго допущения. Разброс значений
1,6% для осевого перемещения является следствием второго допущения. Разброс значений ![]() составляет всего 0,18 % и, объясняется тем, что решения каждого количества сегментов
составляет всего 0,18 % и, объясняется тем, что решения каждого количества сегментов ![]() проводились с различными сетками конечных элементов. Погрешности радиальных характеристик
проводились с различными сетками конечных элементов. Погрешности радиальных характеристик ![]() и
и ![]() определяется обоими допущениями, поэтому они существенно больше погрешности осевой характеристики
определяется обоими допущениями, поэтому они существенно больше погрешности осевой характеристики ![]() . Уже при количестве сегментов
. Уже при количестве сегментов ![]() погрешности укладываются в диапазон 7% и уменьшаются с увеличением количества сегментов. Это можно объяснить тем, что при большем количестве сегментов снижается влияние допущения о постоянстве зазора в каждом сегменте. В то же время, движение воздуха в соседних сегментах считалось независимым. Поэтому при увеличении количества сегментов и границ между ними увеличивается влияние границ. Этим можно объяснить увеличение погрешностей
погрешности укладываются в диапазон 7% и уменьшаются с увеличением количества сегментов. Это можно объяснить тем, что при большем количестве сегментов снижается влияние допущения о постоянстве зазора в каждом сегменте. В то же время, движение воздуха в соседних сегментах считалось независимым. Поэтому при увеличении количества сегментов и границ между ними увеличивается влияние границ. Этим можно объяснить увеличение погрешностей ![]() и
и ![]() при увеличении количества сегментов с девяти до восемнадцати. Скорее всего, если бы геометрия области позволила провести расчет с большим количеством сегментов, погрешность определения радиальных характеристик выросла бы еще больше.
при увеличении количества сегментов с девяти до восемнадцати. Скорее всего, если бы геометрия области позволила провести расчет с большим количеством сегментов, погрешность определения радиальных характеристик выросла бы еще больше.
5. Заключение
В статье предложена сегментная модель, позволившая по предварительной серии вычислений определять реакции сферической опоры в зависимости от смещений и скорости центра сферы с помощью элементарных математических операций. Предложенная модель позволила существенно упростить определение пространственных статических и динамических характеристик шпинделя, на сферических аэростатических опорах: несущую способность, жесткость, частоты свободных колебаний, динамические отклики… Она будет применена для проектирования и оптимизации шпиндельных узлов с аэростатическими сферическими поверхностями и пористыми сопротивлениями наддуву, выпускаемых ОАО "Ресурс точности". Работа выполнена при поддержке целевой программы "Развитие научного потенциала высшей школы (2009-2010 годы)" № 2.1.2/5277.
6. Список литературы
[1]. Пешти Ю.В. Газовая смазка. М.: Издательство МГТУ, 1993. 381 с.
2. Константинеску В. Н. Газовая смазка. М.: Издательство Машиностроение, 1968. 709 с.
3. Эксплуатационные характеристики газовых опор высокоскоростных шпиндельных узлов/ А.В. Космынин [и др.] М.: Издательство Академия Естествознания, 2005. 218 с.
4.Xuhong Li., Hejun Du., Bo Liu; Gih Keong Lau. Numerical simulation of slider air bearings based on a mesh-free method for HDD applications. Microsyst Technol. 2005. №11.Издательство Springer-Verlag. 797-804.
5. Карякин Ю.Е., Сипенков И.Е., Заблоцкий Н.Д. Сферический газовый подшипник скольжения с принудительным наддувом. Механика жидкости и газа. 1970. №3. С.147-154.
6. Прецизионные опоры качения и опоры с газовой смазкой/ С.В. Пинегин [и др.]. М.: Издательство Машиностроение, 1984. 216 с.
7. Заблоцкий Н.Д. Использование схемы непрерывного наддува к расчету газовых подшипников с дискретным наддувом. Тр. ЛПИ. 1965. №248. С.35-44.
Публикации с ключевыми словами: сферическая аэростатическая опора, пористые ограничители наддува, статические силовые характеристики, динамические силовые характеристики, сегментная модель
Публикации со словами: сферическая аэростатическая опора, пористые ограничители наддува, статические силовые характеристики, динамические силовые характеристики, сегментная модель
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||