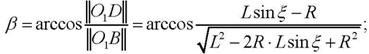научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
УДК 517.977
МГТУ им. Н.Э.Баумана
Пусть движение динамического управляемого объекта (ДУО) в мгновенной плоскости наведения описывается системой дифференциальных уравнений
| (1) |
где ![]() — скорость ДУО,
— скорость ДУО,
![]() — координаты ДУО в нормальной земной системе координат
— координаты ДУО в нормальной земной системе координат![]() ,
,
![]() — угол поворота траектории (см. рис. 1),
— угол поворота траектории (см. рис. 1),
nz— максимальное значение нормальной перегрузки,
![]() — управление, удовлетворяющее ограничению
— управление, удовлетворяющее ограничению ![]() .
.

Рис. 1. Система координат
Система (1) часто используется при описании движения транспортного средства или самолета в горизонтальной плоскости.
На рис. 1 обозначено ![]() – вектор позиции системы (1),
– вектор позиции системы (1), ![]() — произвольное состояние системы (1) в момент времени t0.
— произвольное состояние системы (1) в момент времени t0.
Интегрированием системы дифференциальных уравнений (1) может быть найдено аналитическое решение при использовании следующих типов программных управлений:
1) ![]() .
.
Пусть начальные условия имеют вид
| (2) |
Тогда аналитическое решение системы (1) при начальных условиях (2) имеет вид

Последние два уравнения соответствуют следующей системе:
| (3) |
| (4) |
Угол ![]() , описываемый при движении по окружности разворота в течение времени
, описываемый при движении по окружности разворота в течение времени ![]() , далее будем называть центральным углом разворота.
, далее будем называть центральным углом разворота.
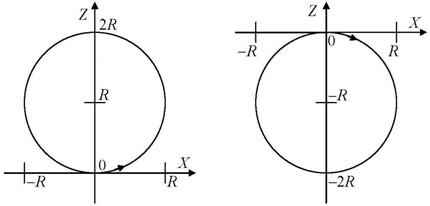
Рис. 2. Движение системы (1) при управлении ![]() .
.
2) ![]() .
.
Пусть начальные условия имеют вид
![]()
Тогда аналитическое решение системы (1) имеет вид:
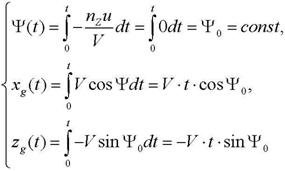
Система уравнений (1) при управлении ![]() описывает прямолинейное движение с начальным углом к оси
описывает прямолинейное движение с начальным углом к оси ![]() , равным
, равным ![]() .
.
Таким образом, движение ДУО с динамикой (1) в классе кусочно-постоянных управлений представляет собой комбинацию прямолинейных участков и участков движения (3) по окружности, радиус которой Rопределяется уравнением (4).
Для описанного класса движений рассматривается задача обеспечения траекторной безопасности при наличии в плоскости, в которой движется ДУО, запрещенной зоны (ЗЗ), имеющей вид круга известного радиуса r.
При определении направлений движения, опасных с точки зрения возможности попадания в ЗЗ возможны следующие 2 варианта.
1) Радиус запрещенной зоны r = 0, тогда ЗЗ вырождается в запрещенную точку ![]() . Необходимо определить центральный угол
. Необходимо определить центральный угол ![]() , на который должен развернуться ДУО для того, чтобы вектор его скорости был ориентирован на эту точку.
, на который должен развернуться ДУО для того, чтобы вектор его скорости был ориентирован на эту точку.
Траектория движения ДУО будет состоять из двух участков: участка разворота по траектории максимальной кривизны до направления на точку ![]() и прямолинейного участка движения. На рис. 3 представлена иллюстрация данной задачи. Траектория движения состоит из отрезка дуги OA траектории разворота максимальной кривизны, представляющей собой окружность радиуса Rс центром в точке O1 и прямолинейного участка движения AB, являющегося отрезком касательной к данной окружности, проходящей через точку B.
и прямолинейного участка движения. На рис. 3 представлена иллюстрация данной задачи. Траектория движения состоит из отрезка дуги OA траектории разворота максимальной кривизны, представляющей собой окружность радиуса Rс центром в точке O1 и прямолинейного участка движения AB, являющегося отрезком касательной к данной окружности, проходящей через точку B.
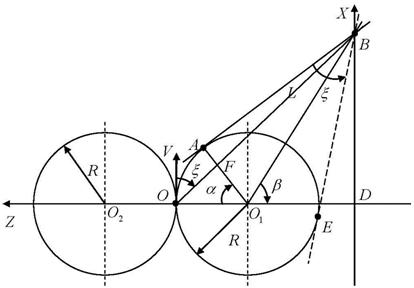
Рис. 3. Построение траектории движения ДУО
На рис. 3 введены следующие обозначения:
![]() — угол пеленга на точку B;
— угол пеленга на точку B;
![]() — центральный угол разворота;
— центральный угол разворота;
![]() — угол направления на точку Bиз центра O1 окружности разворота;
— угол направления на точку Bиз центра O1 окружности разворота;
L— расстояние от точки O до точки B.
Необходимо отметить, что для одной окружности можно провести две различные касательные, проходящие через заданную точку вне окружности. На рис. 3 это прямые ABи BE. Однако только касательная AB удовлетворяет направлению обхода траектории разворота максимальной кривизны – окружности радиуса Rс центром в точке O1, поэтому касательная BE не рассматривается (на рис. 3 показана пунктиром).
Из рис. 3 величины углов соответственно равны
| (5) |
| (6) |
Утверждение 1. Центральный угол разворота до направления на произвольную запрещенную точку Bопределяется выражением (6).
2) Случай статичной круговой ЗЗ ненулевого радиуса r> 0.
Между двумя окружностями можно провести 4 различных касательных. Обозначим их через l1,…, l4 в направлении обхода по окружности. Лишь две из них будут удовлетворять направлению поворота ДУО по траектории предельной кривизны радиуса R. Иллюстрация данного утверждения приведена на рис. 4, где касательные l1 и l2 удовлетворяют направлению движения по траектории разворота (окружность с центром в точке ![]() ), а касательные l3 и l4 являются в данном случае траекториями, приводящими ДУО на круговую траекторию с центром в точке
), а касательные l3 и l4 являются в данном случае траекториями, приводящими ДУО на круговую траекторию с центром в точке ![]() , а не уводящими с нее, таким образом, их можно не рассматривать.
, а не уводящими с нее, таким образом, их можно не рассматривать.

Рис. 4. Касательные к траектории предельной кривизны ДУО и ЗЗ
Таким образом, имеется две касательные, проходящие через окружность траекторию разворота максимальной кривизны. Точки касания этой окружности A1 и A2 будут задавать центральные углы α1 и α2, на которые должен повернуть ДУО, чтобы вектор его скорости был ориентирован в направлении точек C1 и C2 соответственно. Данные два угла будут определять диапазон опасных направлений ![]() .
.
Рассматривается движение ДУО в стартовой системе координат OXcZc.
На рис. 5 введены следующие обозначения: ![]() ,
, ![]() .
.
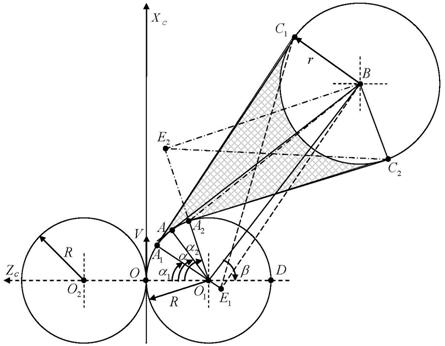
Рис. 5. Построение граничных углов диапазона опасных направлений
Искомый угол ![]() может быть найден из следующего выражения
может быть найден из следующего выражения
| (7) |
Длина ![]() из треугольника
из треугольника ![]()
| (8) |
Координаты точки A2
| (9) |
Координаты точки C2:
| (10) |
Далее необходимо определить угол α1.
Можно выделить 3 варианта расположения точки E1 как следствия соотношения радиуса окружности разворота максимальной кривизны Rи радиуса запрещенной зоны r
![]()
1) R < r. Данный случай иллюстрирует рис. 5. Точка E1 лежит вне пределов отрезка O1A1.
В этом случае искомый угол α1 можно определить из выражения
| (11) |
2) r = R. В этом случае для расчета угла α1 можно воспользоваться формулой (6), полученной для случая запрещенной точки, считая запрещенной точку C1
| (12) |
Данный случай представлен на рис. 6.
3) R> r. В этом случае точка E1 будет принадлежать отрезку O1A1. Рис. 7 иллюстрирует данный случай.
Тогда искомый угол ![]() может быть найден из уравнения
может быть найден из уравнения
| (13) |

Утверждение 2. Зона опасных траекторий (ЗОТ) для ЗЗ радиуса r определяется двумя общими касательными ЗЗ и окружности радиуса R – траектории разворота ДУО максимальной кривизны с центральными углами разворота α1 и α2, где угол α2 определяется выражением (7), а угол α1 для R < rвыражением (11), для R= r — выражением (12), а для R> r — выражением (13).
![]()
Координаты точки A1:
| (14) |
Координаты точки ![]() :
:
| (15) |
Если угол разворота на необходимое направление полета ДУО принадлежит диапазону опасных углов ![]() , то следует выполнить построение границы ЗЗ
, то следует выполнить построение границы ЗЗ ![]() для того, чтобы вычислить предельное время движения в выбранном направлении до начала выполнения отворота от запрещенной зоны.
для того, чтобы вычислить предельное время движения в выбранном направлении до начала выполнения отворота от запрещенной зоны.
Рассмотрим далее случай, когда ЗЗ подвижна, ![]() .
.
Пусть известно положение центра ЗЗ B(t) в каждый момент времени t, т.е. известен закон движения зоны. Пусть также известен закон изменения радиуса ЗЗ r(t) во времени. Известны начальное положение центра ЗЗ B(t0), начальный радиус зоны r(t0), а также ориентация и величина начального вектора скорости V(t0).
Необходимо найти диапазон центральных углов разворота, опасных для движения ДУО с точки зрения попадания с течением времени в динамическую круговую ЗЗ.
Поскольку ЗЗ движется на плоскости, необходимо определить момент времени, в который ДУО, двигаясь по касательной к траектории разворота максимальной кривизны и запрещенной зоне, достигнет точки касания. Для этого предлагается использовать решение оптимизационной задачи вида
| (16) |
Т.е. необходимо минимизировать по времени расстояние, от точки касания запрещенной зоны Ci касательной до точки ![]() , в которую объект попадает, двигаясь по касательной к ЗЗ. Данная задача демонстрируется на примере, изображенном на рис. 8.
, в которую объект попадает, двигаясь по касательной к ЗЗ. Данная задача демонстрируется на примере, изображенном на рис. 8.
На рис. 8 рассматривается положение ДУО и запрещенной зоны в моменты времени t1, t2, t3: t0 <t1 <t2 <t3
Утверждение 3. Определение ЗОТ при динамическом перемещении ЗЗ с известным законом движения B(t) и r(t) сводится к итерационному по времени ![]() ,… алгоритму минимизации разности расстояний по общим касательным с углами α1 и α2 (см. утверждение 2) за время τ и расстояний до точки касания с ЗЗ с параметрами B(τ) и r(τ).
,… алгоритму минимизации разности расстояний по общим касательным с углами α1 и α2 (см. утверждение 2) за время τ и расстояний до точки касания с ЗЗ с параметрами B(τ) и r(τ).

Рис. 8. Получение траектории облета динамической ЗЗ
Замечание. В общем случае время τ1 прохождения точки C1(τ1) облета зоны с одной стороны не будет равно времени τ2 прохождения точки C2(τ2) облета зоны с другой стороны.
Итерационный алгоритм определения ЗОТ.
1) В момент времени τ определяются положение центра B(τ) и радиус r(τ) запрещенной зоны и фиксируются их мгновенные значения.
2) Определяется ЗОТ в виде диапазона ![]() центральных углов разворота, опасных для движения ДУО, используя Утверждение 3.
центральных углов разворота, опасных для движения ДУО, используя Утверждение 3.
3) Определяется положение ДУО ![]() в момент времени τ.
в момент времени τ.
4) Вычисляются расстояния ![]()
а) Если ![]() , то время τ соответствует времени прохождения ДУО точки касания Ci(τ) динамической ЗЗ.
, то время τ соответствует времени прохождения ДУО точки касания Ci(τ) динамической ЗЗ.
б) В противном случае решается задача численной оптимизации (16). Значение времени τ, которому соответствует min функционала (16) является временем прохождения точки касания динамической запрещенной для движения зоны.
Таким образом, сформирована методика оценки зоны опасных траекторий для обеспечения траекторной безопасности ДУО при движении в плоскости, содержащей динамическую круговую запрещенную зону.
Список использованных источников
1. Алгоритмическое обеспечение траекторной безопасности ЛА / Е.М. Воронов [и др.] // Актуальные проблемы российской космонавтики: Труды ХХХII академических чтений по космонавтике. — М., 2008. — С. 426.
2. Воронов Е.М., Карпунин А.А. Алгоритм оценки границ области достижимости летательного аппарата с учетом тяги // Вестник МГТУ им. Н.Э. Баумана. Приборостроение. — 2007. — № 4. — C. 81 – 99.
3. Воронов Е.М. Методы оптимизации управления многообъектными многокритериальными системами на основе стабильно-эффективных игровых решений. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.
Публикации с ключевыми словами: управление, фазовое ограничение, движение в плоскости, траекторная безопасность, запрещенная зона, облет
Публикации со словами: управление, фазовое ограничение, движение в плоскости, траекторная безопасность, запрещенная зона, облет
Смотри также:
- 77-30569/280337 Аппроксимация участка траектории движения в плоскости динамической управляемой системы при помощи логарифмической спирали
- 77-30569/330374 Практическое управление качеством МАТЕС проекта ROV-гидробота в конкурентной среде соревнований
- 77 - 30569/233615 Синтез управления плоской моделью корабля при неполном измерении вектора состояния
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||