научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
УДК 519.852
МГТУ им. Н.Э.Баумана
Среди задач линейного программирования выделяется класс задач бивалентного программирования, известный как задача «о ранце». Существуют различные методы решения этих задач: метод Гилмора-Гомори, метод «ветвей и границ», метод Фора-Мальгранжа и др.
Классический метод Фора-Мальгранжа предполагает наличие одного критерия стоимостиJ, который подлежит максимизации, и одного ограничения – веса
![]()
где ci– стоимость (эффективность) элемента решения xi;
ai– вес элемента решения xi;
b– максимальный вес для ранца;
n– количество элементов решения xi.
Каждый элемент решения принимает одно из двух значений ![]() , поэтому задача относится к классу задач бивалентного программирования.
, поэтому задача относится к классу задач бивалентного программирования.
Достоинство метода Фора-Мальгранжа заключается в том, что в процессе решения в процедуре предусмотрена проверка решения на оптимальность.
В данной работе предлагается модификация классического метода Фора-Мальгранжа решения задачи «о ранце» для случая, когда имеется более одного ограничения, то есть имеется вектор ограничений
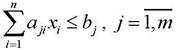
где aji– вес элемента решения xi по j-ому ограничению;
bi– предельный вес для ранца по j-ому ограничению.
Предлагаемый алгоритм состоит из следующей последовательности действий:
Этап 1. Предварительный этап.
а) Проверка существования хотя бы одного решения. Если выполнена система неравенств
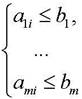
хотя бы для одного элемента решения![]() , то в рассматриваемой задаче хотя бы одно решение существует. В противном случае ненулевого решения не существует и дальнейшее решение может быть остановлено.
, то в рассматриваемой задаче хотя бы одно решение существует. В противном случае ненулевого решения не существует и дальнейшее решение может быть остановлено.
б) Проверка существования тривиального решения. Если выполняется система неравенств
![]()
то в рассматриваемой задаче существует тривиальное решение
![]()
и дальнейшее решение может быть остановлено. В противном случае, переход к следующему пункту.
в) Проводится лексикографическое упорядочивание переменных по убыванию эффективности ![]() и в рассмотрение вводятся новые переменные
и в рассмотрение вводятся новые переменные ![]() такие, что выполняются следующие неравенства
такие, что выполняются следующие неравенства
![]()
При этом, в случае, если ![]() , то в качестве переменной ykнеобходимо выбрать такую, для которой удельная эффективность больше
, то в качестве переменной ykнеобходимо выбрать такую, для которой удельная эффективность больше
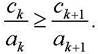
Формируется таблица соответствия переменных xi и yk.
Этап 2. Определение количества нулевых переменных rв решении.
Для определения величины r необходимо найти количество нулевых элементов в решении, допустимое по каждому из ограничений. Для этого из суммы весов всех элементов решения yiпо j-ому ограничению последовательно вычитается максимальный из весов до тех пор, пока разность станет не больше предельного веса ранца по j-ому ограничению, например, если ![]() иначе из полученной разности вычитается следующий наибольший из незадействованных весов,
иначе из полученной разности вычитается следующий наибольший из незадействованных весов,![]() . При выполнении этого неравенства
. При выполнении этого неравенства![]() , иначе процедура продолжается. После определения значений всех
, иначе процедура продолжается. После определения значений всех ![]() необходимо определить количество нулевых элементов в решении для системы ограничений. Для этого необходимо найти наибольшее из найденных значений, поскольку как минимум одно из ограничений начнет выполняться только с этого количества нулевых элементов.
необходимо определить количество нулевых элементов в решении для системы ограничений. Для этого необходимо найти наибольшее из найденных значений, поскольку как минимум одно из ограничений начнет выполняться только с этого количества нулевых элементов.
![]()
Этап 3. Определение количества сочетаний вариантов решений, в которых из общего количества nэлементов r будут нулевыми, а остальные равны единице.
![]()
Этап 4. Генерация ![]() уникальных вариантов решений в порядке убывания суммарной эффективности решений и заполнение таблицы, заголовочная строка которой представлена в таблице 1.
уникальных вариантов решений в порядке убывания суммарной эффективности решений и заполнение таблицы, заголовочная строка которой представлена в таблице 1.
Таблица 1
Варианты решений задачи
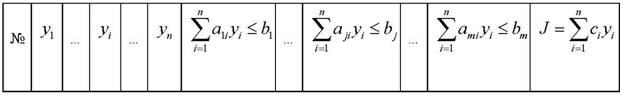
В таблице 1 в столбце № записывается номер варианта решения, в столбцы ![]() вносятся значения элементов рассматриваемого варианта решения. Последний столбец для рассматриваемого варианта решения заполняется, если выполнены все ограничения в столбцах
вносятся значения элементов рассматриваемого варианта решения. Последний столбец для рассматриваемого варианта решения заполняется, если выполнены все ограничения в столбцах![]() . В противном случае это решение будет недопустимо как минимум одним из ограничений.
. В противном случае это решение будет недопустимо как минимум одним из ограничений.
Этап 5. В таблице 1 определяется вариант решения с наибольшей эффективностью (множество вариантов с одинаковой наибольшей эффективностью). Если в таблице 1 не существует ни одного допустимого системой ограничений варианта решения, то количество нулевых элементов в решении увеличивается на 1
![]()
и осуществляется возврат на этап 3.
Этап 6. Выполняется проверка выбранного варианта на оптимальность. Для этого формируются множества![]() .
.
Для того чтобы решение было оптимальным, необходимо выполнение следующего условия
![]() , где
, где
где ![]() - ближайшее к минимальному значение из множества M+.
- ближайшее к минимальному значение из множества M+.
Если условие не выполняется, то потенциально может существовать решение с большей эффективностью с большим количеством нулевых элементов. Для проверки данного предположения количество элементов в решении увеличивается на 1
![]()
и осуществляется возврат на этап 3. После повторного решения задачи найденное оптимальное решение сравнивается с полученным при меньшем количестве нулевых элементов в решении. Из полученных вариантов в результате выбирается вариант, дающий наибольшую эффективность.
Этап 7. Осуществляется обратное переобозначение переменных.
Этап 8. Выполняется проверка правильности решения задачи подстановкой в исходную систему полученного после переобозначения варианта решения задачи.
Этап 9. Записывается ответ задачи.
Замечание. Переобозначение переменных в п. 1(в) в сочетании с п. 7 не является обязательным. Данные операции введены для получения решения с наибольшей эффективностью в первых строках таблицы решений.
Таким образом, представленная процедура позволяет найти решение задачи бивалентного программирования в случае наличия вектора ограничений.
Рассмотрим пример, демонстрирующий работу описанного алгоритма решения задачи «о ранце» с вектором ограничений.
Пример.
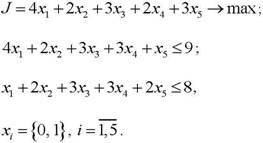
Решение
1) Предварительный этап.
а) Проверка существования хотя бы одного решения

Например, для i= 5 одновременно выполняются такие условия
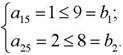
Значит, хотя бы одно решение существует.
б) Проверка существования тривиального решения
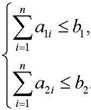
![]() , значит, тривиального решения нет.
, значит, тривиального решения нет.
2) Определяем количество нулевых переменных в решении. Для этого необходимо рассчитать количество нулевых переменных, определяемое каждым из ограничений.
![]()
![]()
Тогда количество нулевых переменных в решении
![]()
3) Определение количества сочетаний вариантов решений, в которых из 5 элементов 1 будет нулевой, а остальные равны единице.
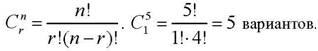
4) Формирование таблицы, содержащей варианты решения
Таблица 2
Варианты решения с одной нулевой переменной
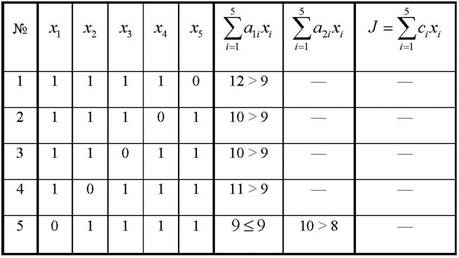
В таблице 1 нет ни одного допустимого решения, необходимо увеличить количество нулевых переменных на единицу: r = 2.
5) Определение количества сочетаний вариантов решений, в которых из 5 элементов 2 будут нулевыми, а остальные равны единице.
![]()
6) Формирование таблицы, содержащей варианты решения
Таблица 3
Варианты решения с двумя нулевыми переменными
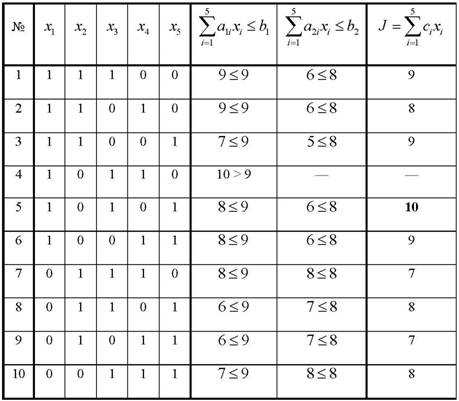
7) Проверка выбранного варианта на оптимальность. Формируются множества ![]() .
.
![]()
Для оптимальности решения необходимо выполнение следующего условия
![]()
3+3 > 2, условие выполнено.
Таким образом, найденное решение является оптимальным.
Ответ: ![]() .
.
Список использованных источников
1. Плотников В.Н., Зверев В.Ю. Принятие решений в системах управления. — М.: Изд-во МГТУ, 1993. — Ч.1. Теория и проектирование алгоритмов принятия оперативных решений. — 172 с.
2. Плотников В.Н., Зверев В.Ю. Принятие решений в системах управления. — М.: Изд-во МГТУ, 1994. — Ч.2. Теория и проектирование алгоритмов принятия проектных решений для многообъектных распределенных систем управления. — 146 с.
Публикации с ключевыми словами: задача комплектования, задача «о ранце», вектор ограничений, бивалентное программирование, целочисленное программирование, пример решения
Публикации со словами: задача комплектования, задача «о ранце», вектор ограничений, бивалентное программирование, целочисленное программирование, пример решения
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



