научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
УДК. 21474
МГТУ им. Н. Э. Баумана
Введение
Одно из важнейших применений спектроскопии комбинационного рассеяния света (эффект Рамана) заключается в определении молекулярного состава образца по спектральным линиям, возникающим в спектре рассеянного излучения, которых нет в спектре первичного излучения (возбуждающего света). В данной работе описывается метод генетического программирования, предназначенный для классификации спектров комбинационного рассеяния света по их компонентному составу.
Генетическое программирование имеет преимущество над искусственными нейронными сетями и хемометрическими методами идентификации состава вещества по его рамановскому спектру, заключающееся в том, что сгенерированные правила распознавания поддаются интерпретации и могут быть использованы как отдельно, так и совместно с экспертной оценкой для классификации спектров.
Распознаванию спектров комбинационного рассеяния света препятствует ряд проблем. Присутствие флуоресцентных соединений, примесей и сложных смесей добавляют трудности при идентификации соединений по их спектрам. Более того, концентрация исследуемого компонента бывает так мала, что она находится вблизи границы предела обнаружения используемого измерительного инструмента. Кроме того, самые интенсивные пики в спектрах компонентов вещества могут приходиться на одну область в спектре исследуемого вещества.
Также существуют трудности, вызванные тем, что спектры рамановского рассеяния обладают высокой разрядностью и низкой численностью. Зачастую приходится идентифицировать вещества, основываясь на малом количестве справочных спектров.
В ответ на это, вместо того, чтобы иметь целью лишь эволюцию правил, корректно классифицирующих обучающие выборки данных, необходимо также оптимизировать выбор правил с тем, чтобы минимизировать вероятность ошибочной классификации будущих выборок, тем самым минимизировав проблемы, связанные с малым количеством образцов и их спектров [1].
Главная задача представленного метода заключается в точном определении вхождения определенного компонента в исследуемое вещество по его спектру комбинационного рассеяния света.
1 Классификация компонентов вещества
В данной работе каждая особь разработанного генетического алгоритма представляет собой математическую формулу, составленную из функций и переменных. К функциям относятся простые математические операторы «+» и «», а переменные соответствуют длинам волн спектра. Популяция инициализируется случайными сочетаниями функций и переменных для создания бинарных деревьев ограниченной глубины ![]() (в данной работе
(в данной работе ![]() ).
).
В совокупности функции и длины волн, выбранные особью ![]() , формируют формулу Ei, вычисление значения которой по соответствующим интенсивностям для заданного спектра Sj, дает значение Ei(Sj).
, формируют формулу Ei, вычисление значения которой по соответствующим интенсивностям для заданного спектра Sj, дает значение Ei(Sj).
Значение Ei(Sj) интерпретируется как индикатор присутствия (Ei(Sj) ≥ 0) либо отсутствия (Ei(Sj) < 0) соответствующего компонента в веществе.
После инициализации популяции вычисляется приспособленность каждой ее особи (формулы) и самые «удачные» (приспособленные) особи отбираются для скрещивания, получая в результате следующее поколение популяции [1].
Выбранная в работе стратегия «разведения» особей заключается в применении принципов элитизма, перекрестного скрещивания и мутации.
Элитизм подразумевает копирование двух самых приспособленных особей из каждой популяции в следующее поколение без изменений (мутаций). Остальные особи нового поколения создаются с помощью перекрестного скрещивания популяции, которое заключается в случайном выборе двух особей с учетом равномерного распределения из лучших 1.5% особей предыдущей популяции и создания нового индивида, сочетающего свойства обоих родителей. Мутация включает в себя случайные изменения в особи новой популяции и имеет фиксированную вероятность.
Первичная цель эволюции особей является способность корректно классифицировать все обучающие выборки. Однако целесообразным представляется ввод вторичной цели, заключающейся в минимизации риска будущих ошибочных классификаций, а также дополнительной цели, связанной с уменьшением трудоемкости вычислений при классификации.
Для достижения первичной цели приспособленность особи ![]() вычисляется как:
вычисляется как:
| (1.1) |
где Aj(Sj) является характеристикой точности классификации особью ![]() спектра Sj, а Nt– количество спектров в обучающей выборке. С помощью характеристики точности Aj(Sj), оценка в +1 балл присваивается особи за каждый правильно классифицированный спектр и –2 балла – за каждую ошибочную классификацию (ложно-положительные и ложно-отрицательные результаты).
спектра Sj, а Nt– количество спектров в обучающей выборке. С помощью характеристики точности Aj(Sj), оценка в +1 балл присваивается особи за каждый правильно классифицированный спектр и –2 балла – за каждую ошибочную классификацию (ложно-положительные и ложно-отрицательные результаты).
Для достижения вторичной цели необходим механизм, с помощью которого, в случае, если две особи одинаково корректно классифицируют выборку, предпочтение отдавалось бы особи, обладающей наибольшей степенью уверенности. Степень уверенности классификации Cj(Sj) особи ![]() по отношению к спектру Sjможно задать как:
по отношению к спектру Sjможно задать как:
| (1.2) |
Для достижения вторичной цели, приспособленность особи ![]() целесообразно принимать за:
целесообразно принимать за:
| (1.3) |
Иными словами, ![]() отражает наименьшую степень уверенности для всех спектров в обучающей выборке: если особь ошибочно классифицирует хотя бы один элемент обучающей выборки, ее значение
отражает наименьшую степень уверенности для всех спектров в обучающей выборке: если особь ошибочно классифицирует хотя бы один элемент обучающей выборки, ее значение ![]() обнуляется.
обнуляется.
В результате ![]() не влияет на приспособленность, пока особь не сможет корректно идентифицировать все обучающие выборки. F2 выступает в качестве критерия ранжирования для тех особей, которые приспособились корректно распознавать все обучающие выборки. Это способствует эволюции особей с более высокими степенями уверенности, уменьшая, тем самым, риск ошибочной классификации спектров при дальнейшем использовании сформированных правил [1].
не влияет на приспособленность, пока особь не сможет корректно идентифицировать все обучающие выборки. F2 выступает в качестве критерия ранжирования для тех особей, которые приспособились корректно распознавать все обучающие выборки. Это способствует эволюции особей с более высокими степенями уверенности, уменьшая, тем самым, риск ошибочной классификации спектров при дальнейшем использовании сформированных правил [1].
Таким образом, с учетом (1.1) и (1.3), суммарная приспособленность особи i вычисляется как:
| (1.4) |
Наиболее приспособленной считается особь с максимальным значением ![]() .
.
Новые популяции продолжают создаваться до наступления состояния схождения. Схождением называется состояние популяции, в котором все особи популяции находятся в области некоторого экстремума и почти одинаковы. Скрещивание практически никак не изменяет популяции, а мутирующие особи склонны вымирать, так как менее приспособлены. Таким образом, схождение популяции означает, что достигнуто решение, близкое к оптимальному [3].
2 Исходные данные моделирования
Исходные данные в данной работе представляют собой спектры комбинационного рассеяния света чистых образцов (содержащих 100% концентрации исходного вещества) [4, 5]. Спектр представлен в виде 2-х мерного целочисленного массива B[w][I], где w–частота, I-интенсивность.
На основании базового набора спектров получают набор обучающих B спектров по следующей формуле:
| (2.1) |
где IB1(ω)…IB5(ω) - базовые спектры, ![]() – j-й обучающий спектр
– j-й обучающий спектр
Значения Cijудовлетворяют системе уравнений:
| (2.2) |
где CB- шаг изменения концентрации для обучающих спектров,![]() .
.
Аналогичным образом получают и набор тестовых T, только с другим шагом изменения концентрации CT.
Таким образом, обучающие и тестовые спектры представляют собой набор линейных комбинаций спектров базового набора B. Шаг изменения концентрации различен при получении обучающего и тестового наборов.
3. Проведение моделирования
В начале для первого базового спектра инициализируется популяция путем задания случайных сочетаний функций и переменных для создания бинарных деревьев ограниченной глубины H (в данной работе H=5).

Рисунок 3.1 - Моделирование процесса эволюции
После инициализации популяции вычисляется приспособленность каждой ее особи по формуле (1.1) и самые «удачные» (приспособленные) особи отбираются для скрещивания, получая в результате следующее поколение популяции [1].
Параллельно со скрещиванием применена стратегия элитизма, которая подразумевает копирование двух самых приспособленных особей из каждой популяции в следующее поколение без изменений.
Затем идет мутация, включающая случайные изменения в особи новой популяции и имеющая фиксированную вероятность.
После мутации идет проверка на наступления состояния схождения и в зависимости от результата идет создание нового поколения, либо выход из цикла и вывод лучшей формулы.
Вычисление функции приспособленности проводится путем применения формулы особи к каждому спектру набора обучающих спектров E. Значение Zm интерпретируется как индикатор присутствия ( Zm ≥ 0 ) либо отсутствия ( Zm < 0 ) соответствующего компонента в веществе. При верном угадывании присутствия или отсутствия компонента в веществе, согласно (1.1), идет увеличении функции приспособленности на 1, при неправильном – уменьшается на 2.

Рисунок 3.2 - Вычисление значения функции приспособленности
Если особь правильно классифицировала все спектры тестового набора T, согласно формуле (1.3), к значению её функции приспособленности прибавляется бонус равный модулю наименьшей степени уверенности особи при классификации тестовых спектров.
4 Результаты моделирования
Результаты процесса моделирования могут быть представлены в виде бинарных деревьев. Пример особей полученных в результате эволюции.
Для 1-го базового спектра:

Рисунок 4.1 - Результат для 1-го базового спектра
1-й базовый спектр имеет максимум на частоте 2400 Гц, поэтому в ходе эволюции была получена формула в которой присутствуют частоты близкие к 2400 Гц со знаком «+».
Для 2-го базового спектра:

Рисунок 4.2 - Результат для 2-го базового спектра
2-й базовый спектр имеет максимум на частоте 2415 Гц. Он несколько сдвинут вправо относительно максимума 1-го базового спектра.
Была выбрана особь в которой со знаком «+» присутствует частота несколько правее максимума, что не дает ложноположительного срабатывания в присутствии первого базового спектра.
Для 3-го базового спектра:
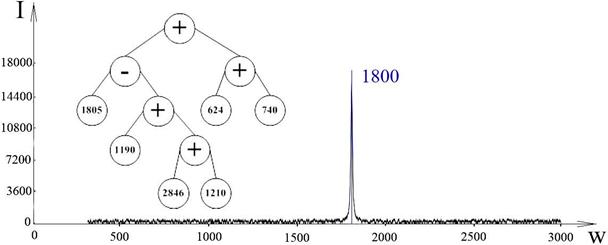
Рисунок 4.3 - Результат для 3-го базового спектра
3-й базовый спектр имеет максимум в районе 1800 Гц. В ходе эволюции была получена особь, имеющая в своей формуле данную частоту. Также любопытно, что формула особи содержит узлы с частотами близкими к 600, 1200 и 2850. Т.к. базовые спектры 4 и 5 имеют максимумы при этих частотах и их присутствие в формуле «защищает» формулу от ложноположительных срабатываний.
Для 4-го базового спектра:

Рисунок 4.4 - Результат для 4-го базового спектра
4-й базовый спектр имеет максимумы в частотах 1800 Гц и 2850 Гц. В полученной особи не присутствует узел с частотой близкой к 1800 Гц. Это можно объяснить тем, что это вело к ложноположительным срабатываниям при присутствии 3-го и 5-го базового спектров, которые также имеют максимум интенсивности при этой частоте.
Для 5-го базового спектра:
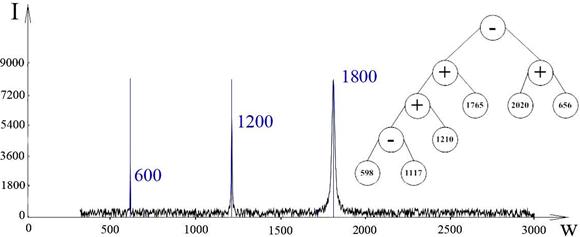
Рисунок 4.5 - Результат для 5-го базового спектра
5-й базовый спектр имеет максимум в точках с частотой 600 Гц, 1200 Гц и 1800Гц. В ходе эволюции выбрана формула, распознающая спектр по характерным максимумам в районе 600Гц и 1200Гц.
5 Алгоритм оценки результатов
Оценка результатов моделирования проводится на тестовых спектрах Т, полученных как набор из линейных комбинаций базовых спектров В.
Функции из набора лучших особей BO последовательно применяется к каждому спектру из набора тестовых спектров T и в зависимости от результата идет увеличение одного из четырех счетчиков.
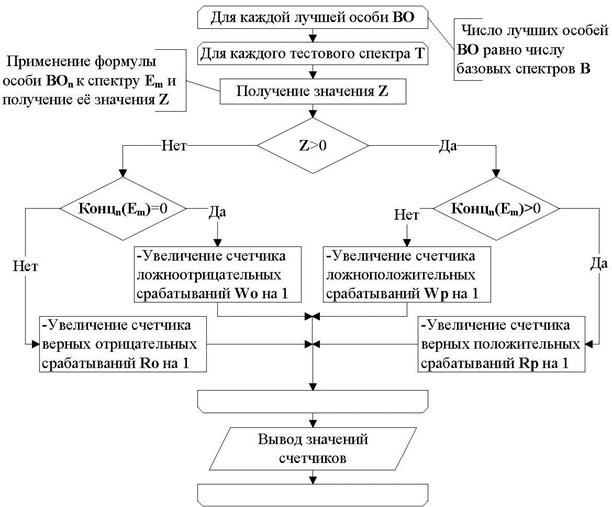
Рисунок 5.1 - Алгоритм оценки результатов моделирования
В ходе тестирования полученных особей проверяется число угадываний и число ошибок при распознавании тестовых спектров. При этом ведется ранжированный учет ложноположительных Wp и ложноотрицательных Wo срабатываний, так как в некоторых случаях один вид ошибки является более критичным, чем другой.
6 Результаты моделирования
В результате эксперимента был промоделирован процесс классификации и произведен ранжированный подсчет ложноположительных Wp и ложноотрицательных Wo, а также число верных положительных Rp и верных отрицательных Ro срабатываний для каждой формулы набора особей BO при классификации набора тестовых спектров T.
Результаты подсчета представлены в виде диаграмм для каждой особи:

Рисунок 6.1 - Результат классификации для 1-й особи
Рисунок 6.1 иллюстрируют эффективность классификации тестовых спектров 1-й особью набора лучших особей BO.
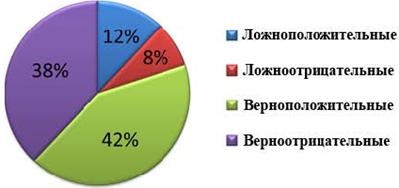
Рисунок 6.2 - Результат классификации для 2-й особи
Рисунок 6.2 иллюстрируют эффективность классификации тестовых спектров 2-й особью набора лучших особей BO.
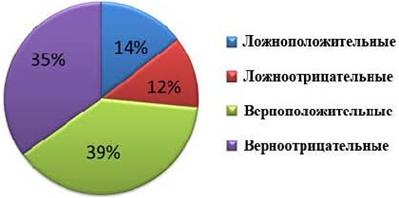
Рисунок 6.4 - Результат классификации для 3-й особи
Рисунок 6.4 иллюстрируют эффективность классификации тестовых спектров 3-й особью набора лучших особей BO.

Рисунок 6.4 Результат классификации для 4-й особи
Рисунок 6.4 иллюстрируют эффективность классификации тестовых спектров 4-й особью набора лучших особей BO.
Подводя итоги, можно сказать, что для повышения эффективности моделирования классификации спектров рамановского рассеяния с использованием генетического программирования требуется решение задачи нахождения оптимальных параметров для моделирования, т.к. изменение этих параметров приводит к улучшению или ухудшению процесса классификации.
Заключение
В данной работе был описан метод генетического программирования для классификации спектров рамановской спектроскопии и представлена двухуровневая функция оценки приспособленности, призванная уменьшить риск ошибочной классификации спектров в будущем.
Сгенерированные правила классификации, полученные методом генной эволюции, позволяют формировать решения, учитывающие экспертный опыт оператора. Они являются информативными при совместном анализе с химической структурой компонента, чьё присутствие в веществе исследуется. Это обстоятельство выгодно отличает представленный метод от других машинных алгоритмов классификации спектров.
Представленный метод генетического программирования оптимизирует степени уверенности в найденных правилах классификации с тем, чтобы уменьшить риск ошибочной классификации спектров при дальнейшем использовании этих правил. Это является полезным в случаях, когда количество обучающих выборок мало.
В дальнейшем представленный метод предлагается совершенствовать с тем, чтобы определять химическую концентрацию каждого компонента вещества по его спектру комбинационного рассеяния света.
Также полезным представляется совершенствование функции приспособленности с целью ранжированного учета ложноположительных и ложноотрицательных срабатываний, так как в некоторых случаях один вид ошибки является более критичным, чем другой.
Список литературы
1. K. Hennesy, etal. An Improved Genetic Programming Technique for the Classification of Raman Spectra // Applications and innovations in intelligent systems XII. Cambridge. 2005. 181-192.
2. Т.В. Панченко. Генетические алгоритмы: учебно-методическое пособие. – Астрахань: Издательский дом «Астраханский университет», 2007. – 87 с.
3. J. Yang, V. Honavar. Featuresubsetselectionusingageneticalgorithm // IntelligentSystemsandtheirApplications, IEEEVol. 13. Iowa State Univ. 2002. 44-49.
4. Власов А.И., Конькова А.Ф. Медико-диагностические экспертные системы для оценки адекватности адаптивной реакции организма на воздействие экстремальных факторов //Конверсия.-1995, №9-10.-С.18-21.
5. А.Н.Бухалто, В.И.Булаев, Е.В.Бурый, А.А.Буянов, А.И.Власов и др. Нейрокомпьютеры в системах обработки изображений. Кн 7. / под общей редакцией Ю.В.Гуляева и А.И.Галушкина. - М.: Радиотехника, 2003. - 192 с.: ил. (серия: Нейрокомпьютеры и их применение).
Публикации с ключевыми словами: генетическое программирование, генетическое программирование, спектров комбинационного рассеяния света, эффекта Рамана
Публикации со словами: генетическое программирование, генетическое программирование, спектров комбинационного рассеяния света, эффекта Рамана
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||






