научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК 621.813, 621.815
МГТУ им. Н.Э. Баумана
Цикл статей посвящен разработке методик расчета соединения двух деталей с цилиндрическими сопрягаемыми поверхностями с малым радиальным зазором и различной жесткостью охватывающей детали. В опубликованных ранее статьях /1–3/ были представлены теоретические основы и инженерная методика расчета соединения деталей по цилиндрическим поверхностям с малым зазором для случая, когда охватывающая деталь безгранична в радиальном направлении.
В данной статье рассмотрен случай, когда охватывающая деталь является тонкостенной, что соответствует зоне I в таблице 1 /1/.
3. Разработка методики расчета для случая, когда охватывающая деталь является тонкостенной.
3.1. Допущения и постановка задачи. Для случая, когда охватывающая деталь является безграничной в радиальном направлении, ее закрепление или уравновешивание может быть различным. Например, она может быть закреплена с помощью заделки, расположенной на большом удалении от отверстия, в которое устанавливается охватываемая деталь. Охватывающая деталь может иметь два удаленных друг от друга одинаковых или различных соединения с охватываемыми деталями и так далее.
Для рассматриваемого случая тонкостенная охватывающая деталь, в отверстие которой с малым зазором устанавливается охватываемая деталь, также должна быть статически уравновешена, но сделать это значительно сложнее.
Для упрощения уравновешивания тонкостенной охватывающей детали примем допущение о том, что охватываемая деталь является абсолютно жесткой, то есть ее контактной податливостью можно пренебречь по сравнению с изгибной податливостью тонкостенной охватывающей детали.
Принятое допущение позволяет рассматривать охватываемую деталь произвольной формы с цилиндрической сопрягаемой поверхностью, что существенно расширяет класс задач, которые можно рассчитывать по разрабатываемой методике. Внутренняя цилиндрическая поверхность охватывающей детали (поверхность отверстия) также является сопрягаемой поверхностью.
При разработке методики расчета будем считать, что цилиндрическая сопрягаемая поверхность охватываемой детали протяженнее поверхности, по которой контактируют при действии нагрузки охватывающая и охватываемая детали. Назовем последнюю поверхность контактной.
Сопрягаемые поверхности охватываемой и охватывающей деталей имеют близкие радиусы кривизны. Отсюда протяженность контактной поверхности при действии нагрузки значительная, а действующее на этой поверхности контактное давление мало интенсивное. Это позволяет сделать допущение о том, что контактной податливостью тонкостенной охватывающей детали можно пренебречь по сравнению с ее изгибной податливостью.
Будем считать сопрягаемые поверхности охватываемой и охватывающей деталей гладкими. Это позволит исключить из рассмотрения касательные нагрузки на контактных поверхностях указанных деталей.
Применить описанную модель соединения деталей можно для различных конструкций, но наиболее актуальной областью для этой модели является закрепление заготовок в станочных приспособлениях (в кулачковых оправках, в различных грибковых наладках, в 3-х кулачков патронах и т.д.) для обработки заготовок на различных металлорежущих станках.
Для повышения точности обработки заготовок в условиях серийного производства сопрягаемые поверхности выдвижных кулачков станочных оправок и грибковых наладок стремятся изготовить радиусом, который максимально приближен к минимальному радиусу сопрягаемого отверстия заготовки. Радиальный зазор, который равен разнице указанных радиусов сопрягаемых поверхностей, составляет от 5 до 40-60 мкм в зависимости от величины радиуса отверстия заготовки.
Чтобы упростить установку заготовки в приспособление обычно используют два способа. Первый способ, см. рис. 1а, заключается в том, что кулачки выдвигают за пределы корпуса и шлифуют в размер, обеспечивающий расчетный радиальный зазор. Чтобы заготовка при ее установке в приспособление не задевала кулачки, последние вдвигают в корпус, см. рис. 1б.
Второй способ, см. рис. 1в, заключается в том, что кулачки совместно с корпусом шлифуют в размер, обеспечивающий расчетный радиальный зазор. Затем кулачки вдвигают в корпус на величину превышающую размер «а» или кулачки демонтируют из корпуса, и с наружной цилиндрической поверхности корпуса снимают слой металла глубиной «а». При установке заготовки поступают аналогичным образом.

Рис. 1. Фрагмент кулачковой оправки: а – положение кулачка при обработке его сопрягаемой поверхности «П»; б – положение кулачка при установке заготовки в приспособление; в – положение кулачка при совместной обработке корпуса и кулачка.
Рассмотрим закрепление тонкостенной заготовки (охватывающей детали) nкулачками (охватываемыми деталями), см. рис. 2. В общем случае ![]() .
.

Рис. 2. Схема закрепления заготовки в оправку с n кулачками (слева – до приложения нагрузки; справа – после приложения нагрузки).
На рис. 2: r1 – радиус сопрягаемой цилиндрической поверхности кулачка;
r2 – радиус сопрягаемой цилиндрической поверхности (отверстия) заготовки;
![]() – радиальный зазор;
– радиальный зазор;
rср – радиус срединной поверхности тонкостенной заготовки;
FK – сила на один кулачок со стороны привода оправки;
![]() и
и ![]() – перемещения точек срединной поверхности заготовки под кулачком и строго между кулачками;
– перемещения точек срединной поверхности заготовки под кулачком и строго между кулачками;
Δφ – угол между двумя соседними кулачками.
При этом ![]() – отклонение формы (отклонение от круглости) заготовки, возникающее в связи с ее деформациями при закреплении.
– отклонение формы (отклонение от круглости) заготовки, возникающее в связи с ее деформациями при закреплении.
Для разрабатываемой методики расчета принимает равномерное расположение кулачков по окружности, то есть ![]() . На практике применяются кулачковые оправки с неравномерным расположением кулачков по окружности, см. рис. 3. Для расчета параметров закрепления заготовок в таких оправках необходимо разрабатывать аналогичную методику расчета.
. На практике применяются кулачковые оправки с неравномерным расположением кулачков по окружности, см. рис. 3. Для расчета параметров закрепления заготовок в таких оправках необходимо разрабатывать аналогичную методику расчета.
Для других конструкций, для которых данная модель соединения деталей имеет отличия, также необходимо разрабатывать аналогичные методики расчета.
Данная методика расчета может быть использована для расчетов и конструирования кулачковых оправок, грибковых наладок / 4 /, 3-х кулачковых патронов и других приспособлений при закреплении в них тонкостенных заготовок базовым отверстием.
Целью разрабатываемой методики является определение эпюры контактного давления в стыке кулачок – заготовка и напряженно-деформированного состояния закрепляемой тонкостенной заготовки.

Рис. 3. Кулачковая оправка с неравномерным расположением кулачков по окружности.
Практическая ценность методики заключается /5, 6/:
– в обоснованном выборе размеров кулачков. Если контактная поверхность кулачка протяженнее его цилиндрической сопрягаемой поверхности (если эпюра контактного давления не умещается на сопрягаемой поверхности кулачка), то ребро кулачка может повредить базовое отверстие заготовки. Основываясь на расчеты, необходимо исключить такие повреждения;
– в определении допустимой силы закрепления заготовки кулачком из условий ее прочности и жесткости;
– в определении режимов обработки заготовки и силы резания из условия отсутствия ее проскальзывания в процессе обработки;
– в определении погрешностей формы заготовки при ее закреплении в кулачковой или другой оправке.
Чтобы инженерная методика обладала общностью, теоретические исследования выполнялись в безразмерном виде.
3.2. Теоретические основы, используемые при разработке методики расчета. С учетом сделанных допущений исследования проводились методами строительной механика машин / 7 /. Заготовка считается плоским кольцом. Дополнительное допущение – плоское кольцо нерастяжимое.
На рис. 4 показана расчетная схема кулачка и части заготовки между одноименными сечениями на соседних кулачках после приложения нагрузки на кулачки. Слева внизу на рис. 4 показан кулачок с действующей на него нагрузкой. Указанная часть заготовки условно разделена на два участка: участок «АВ» (см. слева вверху на рис. 4), который взаимодействует с кулачком; свободный участок (см. справа на рис. 4). Эти участки нагружены контактной нагрузкой и внутренними силовыми факторами в местах рассечения заготовки-кольца.
На рис. 4: φ0 – полуугол контакта;
φ – текущая угловая координата на свободном участке заготовки-кольца;
QB и qAB – сосредоточенная сила и распределенное давление, составляющие эпюру контактного давления;
NB и M* – внутренние силовые факторы (нормальная сила и изгибающий момент) на границах зоны контакта при ![]() .
.
Кроме того, введем следующие переменные:
L и h – длина и толщина заготовки-кольца. При этом ![]() ;
;
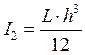 – момент инерции сечения заготовки-кольца;
– момент инерции сечения заготовки-кольца;
Е2 – модуль упругости материала заготовки-кольца.

Рис. 4. Расчетная схема для определения эпюры контактного давления и напряженно-деформированного состояния заготовки-кольца.
3.2.1. Рассмотрим равновесие кулачка. Так как внешняя нагрузка приводится к срединной поверхности заготовки-кольца, примем допущение о том, что распределенное давление qAB действует на цилиндрической поверхности радиуса (![]() ).
).
Учитывая принятое допущение, получим после ряда преобразований следующее выражение
![]() ( 1 )
( 1 )
3.2.2. Рассмотрим участок «АВ» заготовки-кольца в зоне контакта, см. рис. 4.
Учитывая принятые допущения, получим следующее выражение для радиуса срединной поверхности заготовки-кольца после деформирования
![]() ( 2 )
( 2 )
Учтем следующую особенность. Участок «АВ» заготовки-кольца, жестко прилегая к кулачку, имеет постоянную кривизну. Отсюда изгибающий момент на этом участке будет постоянным и равным
 ( 3 )
( 3 )
Для определения распределенного давления qAB используем уравнения равновесия элемента плоского кольца, см. уравнения (4.45) на странице 138 работы / 7 /. Так как изгибающий момент M* = const, касательные силы не учитываются, то распределенное давление будет постоянным и равным
 ( 4 )
( 4 )
В результате деформирования под действием силы FKточка «К» срединной поверхности заготовки-кольца перейдет в положение «К1» на окружности радиуса ρср, см. рис. 5.
На рис. 5: ![]() – угол расположения точки «К» на окружности радиуса rср;
– угол расположения точки «К» на окружности радиуса rср;
![]() – угол расположения точки «К1» на окружности радиуса ρср;
– угол расположения точки «К1» на окружности радиуса ρср;
![]() и
и ![]() – радиальная и касательная (окружная) составляющие общего перемещения точки «К»;
– радиальная и касательная (окружная) составляющие общего перемещения точки «К»;
![]() – угол поворота нормального сечения заготовки-кольца.
– угол поворота нормального сечения заготовки-кольца.

Рис. 5. Расчетная схема для определения перемещения точки К срединной поверхности заготовки-кольца.
Из условия нерастяжимости заготовки-кольца имеем
![]() ( 5 )
( 5 )
Поскольку ![]() , угол поворота нормали к срединной поверхности заготовки-кольца составит
, угол поворота нормали к срединной поверхности заготовки-кольца составит
 ( 6 )
( 6 )
Для определения ![]() и
и ![]() спроецируем четырехугольник
спроецируем четырехугольник ![]() на касательную и нормаль. Учитывая малость углового перемещения (
на касательную и нормаль. Учитывая малость углового перемещения (![]() ;
; ![]() ), получим
), получим
 ( 7 )
( 7 )
 ( 8 )
( 8 )
Из уравнения равновесия участка «АВ» заготовки-кольца, см. рис. 4, получим
![]() ( 9 )
( 9 )
3.2.3. Рассмотрим участок заготовки-кольца свободный от нагрузки. Для него ![]() , см. рис. 4.
, см. рис. 4.
Уравнение равновесия этого участка заготовки-кольца имеет вид
 ( 10 )
( 10 )
Для составления уравнения перемещений свободного от нагрузки участка заготовки-кольца используем дифференциальное уравнение упругой линии плоского кольца
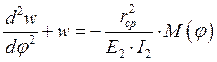 , ( 11 )
, ( 11 )
где текущий внутренний изгибающий момент равен
![]() ( 12 )
( 12 )
Для плоских колец линейные перемещения ![]() и
и ![]() и угол
и угол ![]() поворота нормального сечения кольца связаны между собой следующими зависимостями / 7 /
поворота нормального сечения кольца связаны между собой следующими зависимостями / 7 /
 ( 13 )
( 13 )
 ( 14 )
( 14 )
После интегрирования дифференциального уравнения ( 11 ) и использования уравнений ( 13 ) и ( 14 ), получим после целого ряда преобразований следующие зависимости для определения:
– радиального перемещения точек срединной поверхности заготовки-кольца
 ( 15 )
( 15 )
– касательного (окружного) перемещения точек срединной поверхности заготовки-кольца
 ( 16 )
( 16 )
– угла поворота нормального сечения заготовки-кольца
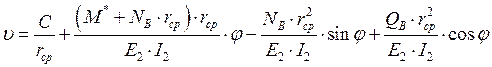 ( 17 )
( 17 )
где: А, В, С – произвольные постоянные.
3.3. Составление системы уравнений и ее решение. Исходными данными являются размеры заготовки и ее материал. При этом важнейшим является диаметр отверстия заготовки с полем допуска. Далее назначают радиальный зазор и определяют радиус сопрягаемой поверхности кулачка.
Из условия надежного закрепления заготовки определяют максимальный крутящий момент МКР от сил резания / 5 / и силу FK, действующую с одного кулачка на заготовку. Отсюда МКР и FK также можно считать заданными параметрами. Затем надо определить полуугол контакта φ0, ширину кулачка, перемещения точек срединной поверхности заготовки под кулачком ![]() и строго между кулачками
и строго между кулачками ![]() , отклонение формы заготовки
, отклонение формы заготовки ![]() и напряженное состояние заготовки. Получить для заданной силы FK аналитические зависимости для искомых параметров невозможно, так как это связано с решением системы трансцендентных уравнений.
и напряженное состояние заготовки. Получить для заданной силы FK аналитические зависимости для искомых параметров невозможно, так как это связано с решением системы трансцендентных уравнений.
Поэтому определение искомых параметров можно осуществить численно методом перебора по программе для ЭВМ (перебор позволяет найти решение, для которого расчетное значение FKпримерно равно заданному значению FK) или по графикам, которые также строятся с помощью расчетов на ЭВМ, но уже по другой программе. В любом случае исходным для расчетов параметром является полуугол контакта φ0, а остальные искомые параметры рассчитываются в зависимости от значения полуугла контакта.
Выберем вариант с графиками, которые являются наглядными и позволяют произвести анализ представленных на них данных. Графики будем строить для кулачковых оправок с тремя кулачками (![]() ).
).
При построении графиков будем выполнять расчеты с переборами двух параметров:
– безразмерного радиального зазора  ;
;
– безразмерной силы, действующей на один кулачок,  .
.
Задается конкретное значение полуугла контакта φ0. Для определения десяти неизвестных (А; В; С; M*; NB; QB ; ![]() ;
; ![]() ; qAB; FK) составляется система линейных алгебраических уравнений, в которую входят уравнения ( 1 ), ( 3 ), ( 9 ), ( 10 ) и следующие зависимости
; qAB; FK) составляется система линейных алгебраических уравнений, в которую входят уравнения ( 1 ), ( 3 ), ( 9 ), ( 10 ) и следующие зависимости
![]()
![]()
![]()

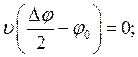
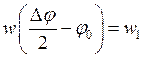 ,
,
Указанная система уравнений решается по программе на ЭВМ. Далее значение полуугла контакта φ0 меняется, и расчеты повторяются по той же программе.
ВЫВОДЫ ПО РАБОТЕ
1. Данная статья посвящена разработке инженерной методики расчета соединения деталей по цилиндрическим поверхностям с малым зазором для случая, когда охватываемое тело является тонкостенным.
2. С учетом принятых допущений в основу инженерной методики расчета положены теоретические положения строительной механики машин.
3. Разрабатываемая инженерная методика расчета наиболее актуальна для расчета и конструирования станочных приспособлений и определения напряженно-деформированного состояния закрепляемых в них заготовок.
4. Большое количество независимых переменных не позволяет разработать инженерную методику расчета, охватывающую все возможные случаи практики. Поэтому при разработке методики расчета принято, что кулачки станочного приспособления равномерно расположены по угловой координате.
5. Получить аналитические зависимости для искомых параметров в разрабатываемой инженерной методике невозможно. Поэтому определение искомых параметров можно осуществить численно методом перебора по программе для ЭВМ или по графикам, которые также строятся с помощью расчетов на ЭВМ. В статье выбран вариант с графиками, которые являются наглядными и позволяют произвести анализ представленных на них данных.
СПИСОК ЛИТЕРАТУРЫ
1. Блинов Д.С., Алешин В.Ф. Определение эпюры контактного давления для соединения деталей по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). Электронный журнал «Наука и образование: электронное научно-техническое издание» МГТУ им. Н.Э. Баумана, # 05, май 2011.
2. Блинов Д.С., Алешин В.Ф. Определение напряженно-деформированного состояния охватывающей детали соединения по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). Электронный журнал «Наука и образование: электронное научно-техническое издание» МГТУ им. Н.Э. Баумана, # 06, июнь 2011.
3. Блинов Д.С., Алешин В.Ф. Инженерная методика расчета соединения деталей по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). Примеры. Электронный журнал «Наука и образование: электронное научно-техническое издание» МГТУ им. Н.Э. Баумана, # 06, июнь 2011.
4. Шатилов А.А., Блинов Д.С., Колобов А.Ю. Деформации при закреплении заготовок и точность обработки. – В сб.: Прогрессивная технология конструкционных материалов. – М., 1980, с. 81 – 91.
5. Корсаков В.С. Основы конструирования приспособлений. – М.: Машиностроение, 1983. – 277 с.
6. Станочные приспособления: Справочник. В 2-х томах. / Ред. совет: Б.Н. Вардашкин (пред.) и др. – М.: Машиностроение, 1984. – Т. 1 – 592 с., – Т. 2 – 656 с.
7. Бояршинов С.В. Основы строительной механики машин. – М.: Машиностроение, 1973. – 456 с.
Публикации с ключевыми словами: напряжения, перемещения, соединение деталей, радиальный зазор, полуугол контакта, эпюра контактного давления, тонкостенная охватывающая деталь
Публикации со словами: напряжения, перемещения, соединение деталей, радиальный зазор, полуугол контакта, эпюра контактного давления, тонкостенная охватывающая деталь
Смотри также:
- Определение напряженно-деформированного состояния охватывающей детали соединения по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении).
- 77-30569/315087 Погрешность формы тонкостенной заготовки при ее закреплении кулачками приспособления с учетом размеров площадки контакта сопрягаемых деталей.
- Инженерная методика расчета соединения деталей по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). Примеры.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



