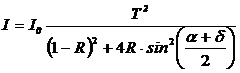научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК. 21474
МГТУ им. Н. Э. Баумана
Введение
В настоящее время большое распространение получили микросистемы, сочетающие в себе различные физические эффекты. Разработка методов моделирования подсистем различной физической природы [1 – 3], а так же методов перехода между подсистемами различной физической природы, является одним из важнейших задач моделирования.
В работе на примере микрооптоэлектромеханического акселерометра на основе интерферометра Фабри-Перо рассматривается моделирование подсистем различной физической природы, а так же методы перехода между ними с использованием языка формального описания VHDL-AMS.
Междисциплинарные связи между подсистемами различной физической природы
В микрооптоэлектромеханических системах [6] можно выделить три основные подсистемы: оптическую, механическую и электрическую/
Оптическая подсистема моделировалась в пакете MATLAB/Simulink. Данный пакет выбран, исходя из совместимости с языком VHDL-AMS.
VHDL это формальный язык описания цифровой аппаратуры. Расширение AMS позволяет описывать смешанные аналого-цифровые устройства. В [4, 7] приведены математические модели оптической подсистемы исследуемого микрооптоэлектромеханического акселерометра:
| (1) | ||
| (2) | ||
|
| и | (3) |
| (4) | ||
| (5) | ||
Выбранные модели были реализованы в специальном модуле в пакете MATLAB/Simulink, позволяющем рассчитывать параметры интерферометра. На основе разработанного программного обеспечения были получены зависимости чистоты отражения от коэффициента отражения зеркала (рис. 1), зависимость коэффициента контрастности от коэффициента отражения (рис. 2), а так же интенсивность излучения после прохождения интерферометра (рис. 3).

Рисунок 1 - Зависимость чистоты отражения от коэффициента отражения зеркала R.

Рисунок 2 - Зависимость коэффициента контрастности от коэффициента отражения зеркала R.

Рисунок 3 - Интенсивность излучения интерферометр после прохождения интерферометра.
Моделирование механической подсистемы проводилось в программном комплексе ANSYS. В качестве объекта моделирования была выбрана подвижная масса микрооптоэлектромеханического акселерометра. На рисунке 4 представлена модель подвижной массы, созданная в программном комплексе ANSYS. Данный программный комплекс для решения использует метод конечных элементов [5]. При моделировании использовалась эквивалентная модель подвижной массы. Входящая в состав программного комплекса утилита ROMTool позволяет представить созданный объект в виде описания на языке VHDL-AMS.

Рисунок 4 – Модель подвижной массы микрооптоэлектромеханического акселерометра.
Для осуществления контроля микрооптоэлектромеханического акселерометра необходима управляющая подсистема. В ее функции входит контроль параметров микрооптоэлектромеханического акселерометра, а так же снятие, преобразование и вывод сигнала. Подсистема представляет собой матрицу светочувствительных диодов, подключенную к усилителю, а затем к модулю сбора, преобразования и вывода информации. Данная система также описывается на языке VHDL-AMS при помощи программного продукта SMASH.
Методы перехода между оптической, механической и управляющей подсистемами, с учетом иерархического подхода, приведены на рисунке 5.
Заключение
Разработка методов переходов между подсистемами различной физической природы, выявление достоинств и недостатков этих методов, а так же их применение для решения практических задач имеет большое значение при проектирование микрооптоэлектромеханических систем.
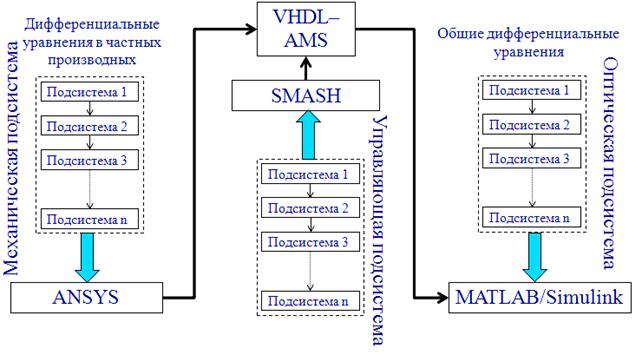
Рисунок 5 – Методы перехода между оптической, механической и управляющей подсистемами.
Преимуществом использования языка VHDL-AMS является его универсальность, возможность описания смешанных аналого-цифровых систем, а так же поддержка многими программными пакетами, используемыми при моделировании микрооптоэлектромеханических систем.
Работа выполнена при частичной поддержке РФФИ (грант 10-07-00171-а).
Литература
1. А.А. Самарский, А.П. Михайлов. Математическое моделирование: Идеи. Методы. Примеры. — М: Наука, 1997. — 320 с.
2. Введение в математическое моделирование. Учебное пособие. Под ред. П. В. Трусова. — М.: Логос, 2004.
3. А. Д. Мышкис. Элементы теории математических моделей. — 3-е изд., испр. — М.: КомКнига, 2007.
4. И.А. Косолапов. Моделирование микроакселерометра на основе интерферометра Фабри-Перов САПР ANSYS, 9 молодежная международная научно-техническая конференция «Наукоемкие технологии и интеллектуальные системы». – М.:МГТУ, 2009. – С.108-111.
5. Р. Галлагер. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984.
6. В.А. Шахнов, Л.А. Зинченко. Особенности математического моделирования в задачах проектирования наносистем. Информационные технологии и вычислительные системы, №4, 2009. С. 84-92.
7. И.А. Косолапов. Иерархическое многомасштабное моделирование микрооптомеханических систем, III Всероссийская школа-семинар для студентов, аспирантов и молодых ученых по направлению «Наноинженерия» - Калуга : КФ МГТУ, 2010. – С.187 – 191.
Публикации с ключевыми словами: микрооптоэлектромеханичские системы, VHDL-AMS, МЭМС
Публикации со словами: микрооптоэлектромеханичские системы, VHDL-AMS, МЭМС
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||