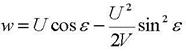научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК. 629.7
МГТУ им. Н. Э. Баумана
Введение
В современных автоматизированных системах (АС) управления воздушным движением (УВД) большое внимание уделяется расчету 4D-траектории воздушных судов (ВС) по данным плана полета, причем повышение достоверности такого расчета является актуальной задачей, поскольку данные расчета используются в задачах распределения плановой информации по диспетчерским рабочим местам, а в системах планирования – для определения загрузок секторов УВД и других элементов воздушного пространства.
Текущие требования к достоверности информации, на основании которой принимаются решения в системах планирования воздушного движения (ПВД), предопределяют учет как можно большего числа факторов при расчете, в противном случае эффективность принимаемых решений в процессах планирования будет снижаться.
Собственно, под расчетом 4D-траектории понимается вычисление времени прохождения ВС последовательных точек маршрута и соответствующих высот от начала до окончания полета на основании данных плана полета, причем под началом полета понимается начало руления, поскольку по правилам заполнения плана полета в нем указывается расчетное время уборки колодок, и именно от этого времени начинается отсчет при расчете 4D-траектории, а под окончанием полета понимается момент освобождения взлётно-посадочной полосы (ВПП), связанный с завершением пробега.
1 Принципы расчета 4D-траектории
При проведении расчетов полет принято рассматривать в последовательном прохождении следующих фаз:
- руление;
- разбег;
- набор высоты до занятия запрошенного эшелона с выходом в крейсерский режим полета;
- полет на эшелоне;
- снижение до захода на посадку (до точки входа в глиссаду);
- посадка;
- пробег.
Поскольку на каждой из перечисленных фаз имеются свои особенности с точки зрения используемых параметров и учитываемых факторов.
В данной статье будет рассмотрен расчет только одной фазы – полета на эшелоне. При полете на эшелоне для расчета траектории используются крейсерская скорость и крейсерский эшелон полета (параметры описываются в плане полета), а расчет производится с учетом ветра.
2 Статистический метод расчета продолжительности полета на эшелоне с учетом эквивалентного ветра
Статистические методы учета ветра упрощаются, если вместо векторных случайных величин оперировать скалярными, введя понятие эквивалентного ветра, равного разности модулей путевой ![]() и воздушной
и воздушной ![]() скоростей, которую обозначим
скоростей, которую обозначим ![]() .
.
При полете по линии ![]() (Рисунок 1.) фактический ветер
(Рисунок 1.) фактический ветер ![]() и фиктивный
и фиктивный ![]() , равный отрезку
, равный отрезку ![]() , дующий строго вдоль линии пути, дадут одинаковое значение путевой скорости.
, дующий строго вдоль линии пути, дадут одинаковое значение путевой скорости.
Эквивалентным ветром называется фиктивный ветер, который, совпадая с линией пути, дает точно такое же значение путевой скорости, что и фактический. Эквивалентный ветер может быть только попутным или встречным.

Рисунок 1 - Расчёт траектории на эшелоне
Найдем скорость эквивалентного ветра, которая по определению равна:
![]()
Учитывая, что
![]() ,
,
где ![]() - угол сноса;
- угол сноса;
ɛ - угол ветра, получим:
![]()
или
![]()
Ввиду того, что углы сноса невелики, можно записать приближенное равенство:
![]()
Тогда
![]() .
.
Подставив в эту формулу значение синуса угла сноса из выражения:

окончательно получим:

Следовательно, путевая скорость, выраженная через эквивалентный ветер, будет равна:

Попутному эквивалентному ветру соответствует знак «плюс», а встречному – «минус».
Можно показать, что эквивалентный ветер не очень сильно изменяется с изменением воздушной скорости и остается справедливым для достаточно большого диапазона воздушных скоростей. Так, например, если эквивалентный ветер рассчитан для воздушной скорости 750 км/час, то при скорости ветра ![]() в диапазоне воздушных скоростей от 600 до 1000 км/час значение эквивалентного ветра можно считать практически неизменным, т.к. величина ошибки
в диапазоне воздушных скоростей от 600 до 1000 км/час значение эквивалентного ветра можно считать практически неизменным, т.к. величина ошибки  от этого допущения не превысит
от этого допущения не превысит ![]() , т.е.
, т.е. ![]() км/час.
км/час.
Значения эквивалентных ветров и их изменчивость определяются на основании статистической обработки данных о ветре для различных маршрутов, высот и сезонов года (месяцев). Обработка данных показывает, что эквивалентные ветры подчиняются нормальному закону распределения, исчерпывающими характеристиками которого являются математическое ожидание ![]() и среднеквадратическое отклонение
и среднеквадратическое отклонение ![]() . Эти значения среднего эквивалентного ветра
. Эти значения среднего эквивалентного ветра ![]() и его изменчивости
и его изменчивости ![]() сводятся в таблицы или атласы.
сводятся в таблицы или атласы.
Зная ![]() и
и ![]() , можно дать вероятностную оценку ожидаемому ветру предстоящему маршруту полета.
, можно дать вероятностную оценку ожидаемому ветру предстоящему маршруту полета.
Для определения вероятности того, что эквивалентный ветер будет заключен в пределах от ![]() до
до ![]() , воспользуемся приведенной функцией Лапласа (рисунок 2.).
, воспользуемся приведенной функцией Лапласа (рисунок 2.).

Рисунок 2 - Функция Лапласа

или
![]()
По этой формуле могут быть найдены значения коэффициентов n.
Для вероятностей ![]() знак у числа nберется положительным, для
знак у числа nберется положительным, для ![]() – отрицательным.
– отрицательным.
Таким образом, для определения того, что ветер по предстоящему маршруту полета с вероятностью ![]() не превысит
не превысит ![]() , можно воспользоваться формулой:
, можно воспользоваться формулой:
![]()
Задаваясь вероятностями ![]() и беря соответствующие значения
и беря соответствующие значения ![]() , можно определить максимальную и минимальную продолжительность полета.
, можно определить максимальную и минимальную продолжительность полета.
При отсутствии данных о фактическом распределении ветра по маршруту расчет выполняется по среднему значению путевой скорости:
![]() ,
,
по которой находится средняя продолжительность полета. Если в это соотношение вместо ![]() подставить
подставить ![]() , то для соответствующей вероятности Pможно оценить, что фактическая путевая скорость будет не меньше некоторого значения Wp.
, то для соответствующей вероятности Pможно оценить, что фактическая путевая скорость будет не меньше некоторого значения Wp.
С помощью эквивалентного ветра можно решать задачи, связанные с оценкой точности выхода на цель во времени.
Если расчет выполнить по среднему значению эквивалентного ветра на маршруте и в полете не принимать мер для своевременного прибытия на цель, строго выдерживая ранее рассчитанный режим работы двигателей, то ошибка во времени выхода на цель будет равна:
![]()
Но ![]() и
и ![]()
Выразив ошибку в минутах, получим:
![]()
Для вероятности 0,95 ошибка во времени выхода на цель будет равна удвоенному значению среднеквадратического отклонения, т.е.

Прибавляя и вычитая Δtк средней продолжительности полета, можно найти ее максимальное и минимальное значения, отнесенные к вероятности P=0,95.
Следует иметь ввиду, что эти формулы, записанные на основании дифференциальных соотношений, дают приближенный результат. При этом погрешность будет тем больше, чем больше изменчивость ветра.
Если экипажу задано точное время прибытия на цель и расчет полета, в том числе и времени вылета, сделан по среднему значению эквивалентного ветра, то по формуле можно оценить величину избытка или недостатка времени. В частности, с вероятностью ![]() его величина не превысит найденной по формуле
его величина не превысит найденной по формуле ![]()
Данные, необходимые для расчета траектории на эшелоне должна содержать следующие параметры и состоять из таблиц:
| (1) |
Где
| (2) |
W- путевая скорость;
V- воздушная скорость;
![]() - скорость эквивалентного ветра;
- скорость эквивалентного ветра;
U- скорость фактического ветра;
![]() - угол ветра.
- угол ветра.
Параметры по эквивалентному ветру (угол и скорость ветра) или присылаются формализовано каждые 3 часа из метеослужбы, или, если такой возможности нет, берутся из таблицы по высотам (статистические данные). Скорость ВС берётся из плана полета, а если в плане полета она не указана, то используется крейсерская скорость для определенного типа ВС на данном эшелоне из лётно-технических характеристик (ЛТХ) ВС. Угол ветра, который участвует в окончательном соотношении (![]() ), пересчитывается на основании присланных метеослужбой данных или на основании данных, взятых из статистических таблиц, в соответствии с направлением участка трассы или маршрута, по которому проходит полет ВС.
), пересчитывается на основании присланных метеослужбой данных или на основании данных, взятых из статистических таблиц, в соответствии с направлением участка трассы или маршрута, по которому проходит полет ВС.
3 Метод расчета через определение угла сноса
Навигационный треугольник скоростей и его элементы представлены на рисунке 3.

Рисунок 3 - Навигационный треугольник скоростей
Треугольник, образованный вектором воздушной скорости, вектором ветра и вектором путевой скорости, называется навигационным треугольником скоростей (Рисунок 4.).
Элементами навигационного треугольника скоростей являются:
· V - воздушная скорость – скорость перемещения ВС относительно воздушной среды;
· W- скорость ветра – скорость перемещения воздушных масс относительно земной поверхности;
· Vn - путевая скорость – скорость перемещения ВС относительно земной поверхности;
· d - направление ветра – измеряется от северного направления меридиана по часовой стрелке от 0° до 360°. В самолетовождении при навигационных расчетах принято брать направление, куда дует ветер. Следовательно, направление навигационного ветра отличается от метеорологического на 180°;
· К - курс ВС – угол в горизонтальной плоскости между северным направлением меридиана и продольной осью ВС;
· УС - угол сноса – угол между векторами воздушной и путевой скорости;
· ПУ - путевой угол – угол между северным направлением меридиана и направлением движения ВС относительно земной поверхности;
· УВ - угол ветра – угол между векторами путевой скорости и скорости ветра;
· КУВ - курсовой угол ветра – угол между вектором воздушной скорости и вектором ветра.
Движение воздуха относительно земной поверхности называется ветром. Скорость и направление ветра характеризуется вектором ветра. В самолетовождении направление ветра измеряется между меридианом и вектором ветра. Этот ветер называется навигационным (куда дует ветер). Направление метеорологического ветра отличается от навигационного на 180° (откуда дует ветер).
Скорость перемещения ВС относительно поверхности Земли называется путевой скоростью.
Угол между вектором воздушной скорости и вектором путевой скорости называется углом сноса. Угол сноса отсчитывается от вектора воздушной скорости вправо (плюсовой) и влево (минусовой).
Путевым углом называется угол между северным направлением меридиана и вектором путевой скорости (линией пути). Он отсчитывается от северного направления меридиана до вектора путевой скорости по ходу часовой стрелки от 0 до 360°. Различают заданный путевой угол ЗПУ и фактический путевой угол ФПУ.
Путевой угол определяется по формуле: ПУ=К+УС
Угол между вектором путевой скорости и вектором ветра называется углом ветра. Угол ветра отсчитывается от вектора путевой скорости до вектора ветра по ходу часовой стрелки от 0 до 360°.
Угол между вектором воздушной скорости и вектором ветра называется курсовым (бортовым) углом ветра Курсовой угол ветра отсчитывается от вектора воздушной скорости до вектора ветра по ходу часовой стрелки от 0 до 360°
Для расчета навигационных элементов полета используются следующие зависимости между элементами навигационного треугольника скоростей:
| (3) |
| (4) |
4 Модель, учитывающая взаимное расположение участка трассы и скорости ветра по GRIB
Входными данными для расчета служат значения скорости и направления ветра, передаваемые различными центрами (Вашингтон, Брекнелл, Москва) в ГСТ в кодах ГРИД или ГРИБ, на уровнях от 1000 до 100 гПа, (в крайнем случае, это могут быть и аэрологические данные, но их слишком мало).
Маршрут полета, описанный в плане полета, и его изменения представляет собой заранее рассчитанную четырехмерную пространственную траекторию полета ВС в виде связанных отрезков линии пути, каждый из которых задан координатами, высотой (эшелоном) и временем прохода пунктов маршрута, в том числе и пунктов изменения профиля полета. На каждом участке скорость ВС раскладывается на составляющие ![]() и
и ![]() (с учетом расположения участка на карте). Далее определяется средний ветер на этом участке, с учетом выбранного эшелона полета, причем учитывается ветер в начале, середине и в конце участка (
(с учетом расположения участка на карте). Далее определяется средний ветер на этом участке, с учетом выбранного эшелона полета, причем учитывается ветер в начале, середине и в конце участка (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ). Для нахождения скорости ветра на эшелоне (уровне полета
). Для нахождения скорости ветра на эшелоне (уровне полета ![]() ), не совпадающем с уровнями отбора данных, применяется логарифмическая интерполяция:
), не совпадающем с уровнями отбора данных, применяется логарифмическая интерполяция:

где ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() - составляющие ветра и давление на уровнях выше и ниже интерполируемого.
- составляющие ветра и давление на уровнях выше и ниже интерполируемого.
Для нахождения скорости ветра на конкретном уровне, но в произвольной точке применяется билинейная интерполяция:

где ![]() ,
, ![]() - значения составляющих скорости ветра в узлах регулярной сетки,
- значения составляющих скорости ветра в узлах регулярной сетки, ![]() ,
, ![]() - шаги сетки.
- шаги сетки.
Средний ветер на участке трассы:

Путевая (суммарная) скорость ВС с учетом ветра:
| (5) |
| (6) |
где ![]() ,
, ![]() - составляющие скорости ВС с учетом ветра. Путевая (итоговая) скорость ВС (
- составляющие скорости ВС с учетом ветра. Путевая (итоговая) скорость ВС (![]() ) определяется как квадратный корень из суммы квадратов
) определяется как квадратный корень из суммы квадратов ![]() и
и ![]() . Зная длину участка
. Зная длину участка ![]() (в км), определяется время в пути:
(в км), определяется время в пути:
| (7) |
| (8) |
Таким образом, на каждом заданном участке трассы определяются истинные скорости ВС.
Литература
1. Гальков М.А., Рудельсон Л.Е., Тверитнев М.М. Имитационная модель использования воздушного пространства // Известия Академии Наук. Теория и системы управления. – 2003. № 4.
2. А.М.Баранов, С.В.Солонин Авиационная метеорология - Ленинград Гидрометеоиздат. 1981.
3. Богаткин О.Г. Авиационная метеорология - РГГМУ. С.-Петербург. 2005 г.
Публикации с ключевыми словами: 4D-траектория, управление воздушным движением, формат GRIB
Публикации со словами: 4D-траектория, управление воздушным движением, формат GRIB
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||