научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2011
УДК 621.396.96
НИИ РЭТ МГТУ им. Н.Э. Баумана
Одним из интересных подходов к обработке распределенных радиолокационных сигналов является подход, основанный на концепции минимально-параметрического моделирования. При этом обработка строится на основе некоторого интегрального преобразования, структурно связанного с моделью сигнала, получаемой как в режиме реального времени, так и заранее. В качестве таких преобразований могут применяться как общеизвестные интегральные преобразования, так и их разновидности и модификации. Выбор эффективного, то есть оптимального в заданных условиях и ограничениях преобразования является задачей, требующей проведения самостоятельных исследований и создания специальной методики. В данном докладе проводится вариант такой методики и результаты ее применения для сравнения преобразований Фурье [1], Вейвлет [2] и свертки в системе эталонных функций [3].
Оптимальность минимально параметрических процедур обработки информации целесообразно рассматривать по критерию максимума отношения правдоподобия при принятии решения на основе решающей статистики, полученной с помощью соответствующего интегрального преобразования. Известно, что максимум отношения правдоподобия в задачах обнаружения, распознавания, измерения и совместных задачах достигается при максимуме отношения сигнал-шум на выходе процедуры формирования решающей статистики. При этом не является определяющим оптимальность процедуры получения собственно решающей статистики. Таким образом, если удается доказать, что при прочих равных условиях процедура обработки сигнала с целью получения решающей статистики обеспечит на выходе максимум отношения сигнал-шум по сравнению с прочими процедурами, то данная обработка будет являться оптимальной по сформулированному выше критерию. Представим обрабатываемый сигнал в виде
| (1) |
включающим истинные значения некоторого набора параметров ![]() , определяемых физическим процессом или явлением, порождающим исследуемый сигнал.
, определяемых физическим процессом или явлением, порождающим исследуемый сигнал.
Применим к сигналу, определяемому выражением (1), преобразование Фурье. Тогда справедливой будет запись
| (2) |
Для упрощения вычисления спектра разложим сигнал, определяемый выражением (2), в гармонический ряд Фурье.
| (3) |
где  - коэффициенты разложения Фурье,
- коэффициенты разложения Фурье, ![]() - длительность принятого когерентного сигнала.
- длительность принятого когерентного сигнала.
Подставим полученный результат (3) в выражение (2). После выполнения соответствующих преобразований над сигналом справедливой будет запись, определяющая разложение сигнала в ряд по набору гармоник
| (4) |
Нетрудно видеть, что каждая из гармоник ![]() , входящая в выражение (4), будет ненулевой. Введем понятие коэффициента полезного действия (КПД) интегрального преобразования в виде:
, входящая в выражение (4), будет ненулевой. Введем понятие коэффициента полезного действия (КПД) интегрального преобразования в виде:
| (5) |
где ![]() - число гармоник в спектре, по которым происходит обнаружение сигнала,
- число гармоник в спектре, по которым происходит обнаружение сигнала,  - энергия сигнала.
- энергия сигнала.
Можно утверждать, что преобразование будет являться оптимальным, если КПД преобразования, определяемый выражением (5), будет стремиться к единице. Исходя из этого, справедливой будет запись:
| (6) |
Представим сигнал ![]() в дискретном виде
в дискретном виде ![]() ;
; ![]() ;
; ![]() .
.
Тогда
| (7) |
В результате получаем выражение для КПД, показывающее предел неоптимальности в рассматриваемом смысле преобразования Фурье.
| (8) |
Полученная количественная оценка дает предельный коэффициент использования энергии сигнала при выполнении преобразований над ним. Превысить данную величину, используя сигнальную обработку, построенную на основе преобразования Фурье, невозможно.
Рассмотрим простейший пример, когда принятый сигнал представляет собой гармоническое колебание на частоте Доплера ![]()
| (9) |
| (10) |
В этом случае для выполнения условия в выражении (6) необходимо, чтобы
| (11) |
где ![]() - номер гармоники в спектре, по которой происходит обнаружение сигнала.
- номер гармоники в спектре, по которой происходит обнаружение сигнала.
Таким образом, для достижения КПД преобразования, равному единице, должно выполняться следующее условие
|
|
При этом выражение для КПД преобразования трансформируется в следующее
| (12) |
где ![]() ,
, ![]() - дробная часть от
- дробная часть от ![]() ,
,![]() .
.
Расчеты показали, что при разных соотношениях величины ![]() КПД преобразования Фурье для простого гармонического сигнала будет колебаться от 0,4 до 1,0. Физический смысл данного положения определяется эффектом просачивания энергии и в данном случае характеризует потери энергии на боковые лепестки в том числе и на так называемые "косые сечения" функции неопределенности сигналов [3].
КПД преобразования Фурье для простого гармонического сигнала будет колебаться от 0,4 до 1,0. Физический смысл данного положения определяется эффектом просачивания энергии и в данном случае характеризует потери энергии на боковые лепестки в том числе и на так называемые "косые сечения" функции неопределенности сигналов [3].
Если в принятом сигнале содержится более одной гармоники, то выражение (12) усложняется. Нетрудно показать, что, как и в предыдущем случае, КПД преобразования будет осциллировать. При выполнении условия (13) оно будет стремиться к единице, а при выполнении условия (14) КПД будет минимальным и равняться примерно 0,4.
| (13) |
где ![]() - гармоники принятого сигнала.
- гармоники принятого сигнала.
| (14) |
Применим к сигналу (1) вейвлет разложение [2]:
| (15) |
где  - вейвлет преобразование сигнала
- вейвлет преобразование сигнала ![]() ,
,  ,
, ![]() - ортонормированный вейвлет - базис.
- ортонормированный вейвлет - базис.
Тогда КПД вейвлет преобразования можно записать в виде
| (16) |
При гладко меняющейся функции ![]() вейвлет разложение может давать достаточно точную аппроксимацию [2], т.е.
вейвлет разложение может давать достаточно точную аппроксимацию [2], т.е. ![]() . Для других видов функций КПД вейвлет преобразования будет сильно зависеть от применяемого базиса
. Для других видов функций КПД вейвлет преобразования будет сильно зависеть от применяемого базиса ![]() .
.
На сегодняшний день существует большое число ортонормированных вейвлет – базисов. Самым первым из них появился вейвлет Хаара, который представляет собой кусочно-постоянную функцию вида
| (17) |
В этом случае для простого гармонического сигнала КПД преобразования равно 1. Однако исследования показали, что с увеличением частоты гармоники и длительности принимаемого сигнала КПД падает. При величине ![]() коэффициент полезного действия вейвлет преобразования оказывается меньше минимально достижимого КПД преобразования Фурье (
коэффициент полезного действия вейвлет преобразования оказывается меньше минимально достижимого КПД преобразования Фурье (![]() ).
).
При наличии в сигнале более одной гармоники КПД вейвлет преобразования также падает, главным образом, за счет увеличения ширины спектра сигнала.
Применим к сигналу (1) преобразование свертки в системе эталонных функций. При этом будем считать, что параметры ![]() свертки структурно совпадают с параметрами сигнала
свертки структурно совпадают с параметрами сигнала ![]() , однако количественно известны с некоторой ошибкой
, однако количественно известны с некоторой ошибкой ![]()
| (18) |
В этом случае выражение свертки в системе эталонных функций трансформируется к виду, определяемому выражением:
| (19) |
где ![]() .
.
Проведем разложение сигнала (1) в ряд по эталонным функциям ![]() , определяемым выражением вида
, определяемым выражением вида
| (20) |
После подстановки разложенного сигнала в выражение (19) и выполнения соответствующих вычислений, на основе данного выражения для сигнатуры рассматриваемого сигнала можно записать:
| (21) |
Применим к данному преобразованию операцию вычисления
| (22) |
Раскрывая данное выражение, нетрудно получить, что при равенстве параметров сигнала ![]() параметрам сигнала
параметрам сигнала ![]() , т.е. при
, т.е. при ![]() , КПД преобразования стремиться к единице.
, КПД преобразования стремиться к единице.
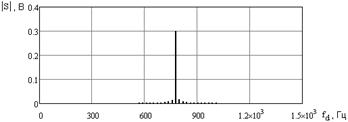
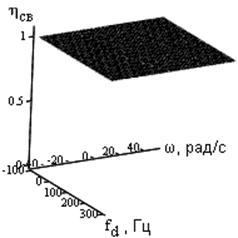
Результаты исследования КПД различных преобразований, рассмотренных выше представлены на рис. 1 в виде зависимостей КПД от характеристических масштабных размерностей преобразований для одиночного и для сложного сигналов.
а) |
б) |
в) |
г) |
д) |
е) |
ж) |
з) |
Рис. 1. а) Одиночный и б) групповой сигналы и соответствующие им КПД преобразований в) Фурье одиночного сигнала г) Фурье группового сигнала, д) Вейвлет одиночного сигнала, е) вейвлет группового сигнала, ж) свертки в системе эталонных Функций одиночного преобразования и з) свертки в системе эталонных функций группового сигнала | |
Как следует из приведенных рисунков, наиболее эффективным является преобразование свертки в системе эталонных функций. Это показывает, что именно это преобразование обеспечивает оптимальную обработку сигнала по критерию максимума отношения правдоподобия. То есть, создает наилучшие условия для обнаружения при прочих равных. Физический смысл данного утверждения заключается в том, что рассматриваемое преобразование обладает фокусирующими свойствами в отношении полезной энергии, содержащейся в принятом сигнале. Вейвлет преобразование оказывается эффективным в низкочастотной области при работе по одиночным сигналам, а Фурье преобразование может эффективно работать только при неограниченной разрешающей способности на длинных выборках. При этом, при фильтрации сигналов от групповых целей достигается энергетическая эффективность не более 80 процентов. Таким образом, применение преобразования свертки в системе эталонных функций и подхода на основе минимально-параметрического моделирования позволяет потенциально достичь выигрыша на 20 процентов по сравнению с потенциальными характеристиками преобразования Фурье.
Список использованных источников:
1. Марпл - мл. С.Л. Цифровой спектральный анализ и его приложения /Пер. с англ. М.: Мир, 1990. 584 с.
2. Мала С. Вэйвлеты в обработке сигналов. Пер. с англ. под ред. Я.М. Жилейкина. М.: Мир, 2005. 672 с.
3. Нефедов С.И., Коротеев Д.Е. Применение адаптивных алгоритмов при оптимальной обработке длительных когерентных сигналов с использованием преобразования свертки в системе // Радиолокация, навигация, связь: Труды XII международной научно-технической конф. Воронеж. 2006. Т. 3. C. 1706 - 1713.
4. Трухачев Л.А. Радиолокационные сигналы и их применения. М.: Военное издательство, 2006. 320с.
Публикации с ключевыми словами: преобразование Фурье, свертка в системе эталонных функций, интегральное преобразование, Вейвлет преобразование, коэффициент полезного действия
Публикации со словами: преобразование Фурье, свертка в системе эталонных функций, интегральное преобразование, Вейвлет преобразование, коэффициент полезного действия
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
 .
. ,
, .
.
 .
. .
.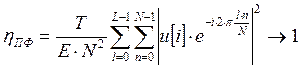 .
.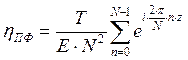 ,
, ,
, ,
,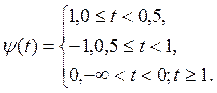

 .
. .
.