научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК 621.396
МГТУ им. Н.Э. Баумана
Особенности Структурной схемы системы ЧАП
В системах радиоуправления широкое применение нашел следящий измеритель радиальной скорости, основанный на измерении текущего доплеровского сдвига частоты принимаемого сигнала. После вхождения в режим слежения измеритель на максимальной дальности формирует оценку относительной скорости сближения.
При построении следящего измерителя постулируется следующие два утверждения. Во-первых, считается, что полезная информация заключена в плавных, сравнительно медленных изменениях доплеровской частоты, вызванных изменением текущего расстояния между источником сигнала и измерителем. Во-вторых, более быстрые, высокочастотные изменения частоты и амплитуды принимаемого сигнала порождены шумами цели и помехами, и поэтому должны быть подавлены.
Следящий измеритель скорости строится по классической супергетеродинной схеме частотной автоподстройки (ЧАП) (рис. 1) и включает три основных блока [1].

Рис. 1. Структурная схема системы ЧАП.
Первым блоком следящего измерителя является дискриминатор, на выходе которого формируется напряжение uд, зависящее от ошибки слежения (рассогласования) измеряемого параметра. В системе ЧАП реализован так называемый “разнесенный” дискриминатор, в котором функция дискриминатора разделена между несколькими устройства. В этом случае входной сигнал uс(t) поступает на сигнальный вход смесителя (См), в котором происходит изменение несущей частоты сигнала fс. На опорный вход См подаются колебания с частотой fг. Составляющая выходного колебания См с частотой fпр фильтруется и усиливается усилителем промежуточной частоты (УПЧ). Напряжение с выхода УПЧ подается на частотный детектор (ЧД), выходное напряжение которого зависит от отклонения Δfпр = fпр - fп , где fп – переходная частота ЧД. При появлении отклонения Δfпр ≠ 0 на выходе ЧД возникает напряжение uд, зависящее от величины и знака Δfпр. Таким образом, разнесенный дискриминатор включает в себя перестраиваемую часть, состоящую из смесителя и УПЧ, и неперестраиваемый частотный детектор, настроенный на постоянную центральную частоту fп.
Напряжение uд фильтруется фильтром нижних частот (ФНЧ), представляющим собой второй блок, принципиально необходимый для построения следящего измерителя. ФНЧ, вырабатывающий регулирующее напряжение uр, играет роль сглаживающей цепи, которая пропускает сравнительно медленные, закономерные изменения принимаемого сигнала, а случайные, более высокочастотные флуктуации частоты сглаживаются (подавляются).
Регулирующее напряжение uр поступает на третий блок следящего измерителя – управляемый генератор (УГ), необходимый для практической реализации измерителя. Под действием uр УГ формирует опорный сигнал uгдискриминатора, изменяя частоту fг, а, следовательно, и частоту fпр так, что исходное рассогласование Δfпр уменьшается. При этом в режиме эффективного слежения частота сигнала uг с некоторым запаздыванием повторяет закономерные изменения частоты принимаемого сигнала. Таким образом, в системе ЧАП реализуется управление по рассогласованию.
Физические и математические модели функциональных устройств системы ЧАП
При исследовании следящих систем частот, выделяющих на выходе оценку λ*(t) измеряемого параметра λ(t), используют метод информативного параметра [1]. В этом методе моделируемая радиосистема с входным сигналом uс[t, λ(t)] и выходным сигналом uг[t, λ*(t)] заменяется зквивалентной системой автоматического управления с входным воздействием λ(t) и выходным сигналом λ*(t).
При реализации метода отдельные блоки структурной схемы заменяются математическими моделями соответствующих звеньев. Сигналы и помехи описываются их комплексными огибающими.
Для получения математического описания системы ЧАП рассмотрим физические и математические модели ее устройств (см. рис. 1) с учетом той роли, которую они играют в процессе регулирования частоты управляемого генератора.
В смесителе происходит преобразование несущей частоты принимаемого сигнала. При гетеродинном преобразовании сигнал с частотой fс и колебания УГ с частотой fгодновременно воздействуют на нелинейный элемент (или на элемент с переменным параметром). В результате на выходе См возникает колебание, имеющее в своем составе составляющие с комбинационными частотами его входных сигналов fс и fг. Одной из комбинационных частот, используемой в качестве новой несущей частоты выходного сигнала, является промежуточная частота fпр.
В следящих измерителях скорости часто применяется верхняя настройка гетеродина, при которой выполняется неравенство fг (t) > fс(t), а промежуточная частота равна
. | (1) |
Для минимизации искажений информации при преобразовании частоты должно выполняться условие Uс << Uг, где Uс и Uг – уровни сигнала и гетеродина. При выполнении этого условия свойства преобразователя частоты не зависят от уровня сигнала. Со спектральной точки зрения в этом случае происходит перенос спектра сигнала в область промежуточной частоты без нарушений амплитудных и фазовых соотношений.
Усилитель промежуточной частоты работает на фиксированной частоте и обеспечивает усиление принимаемого сигнала до уровня, необходимого для эффективной работы ЧД. Номинальное значение промежуточной частоты fпр0 соответствует средней частоте настройки усилителя. Полоса пропускания УПЧ определяется в основном шириной спектра сигнала.
При выборе коэффициента усиления УПЧ для предварительных оценок можно использовать следующие практические рекомендации [2]. На выходе ЧД требуетсяполучить максимальную амплитуду порядка 1 В при напряжении промежуточной частоты на выходе смесителя 0,2 – 0,4 В.
Частотный детектор. В системах слежения за доплеровской частотой могут применяться ЧД различных типов. Для примера рассмотрим типовой ЧД с фазовым преобразованием частотной модуляции [2].
В ЧД этого типа ЧМ колебание преобразуется по амплитуде с последующим применением фазового детектора для выделения модулирующей функции. Детекторная характеристика, представляющая собой зависимость постоянного напряжения на выходе ЧД от отклонения частоты f входного сигнала от его переходной (центральной) частоты fп, имеет вид (рис. 2)
|
(2) |
где ξ = ( f / fп– fп / f)de– обобщенная расстройка; de – затухание контуров резонансной цепи ЧД; p– обобщенный коэффициент связи контуров; uвх – напряжение на входе ЧД; kд – коэффициент передачи, зависящий от электрических параметров схемы ЧД.

Рис. 2. Дискриминационная характеристика частотного детектора.
Выходное напряжение ЧД uд = F(ξ), рассматриваемое как функция x, является нечетной функцией своего аргумента, т. еF(–ξ) = – F(ξ). Физически это свойство означает, что при изменении знака аргумента изменяется знак напряжения uд, что принципиально необходимо для функционирования замкнутых автоматических систем в режиме слежения. Таким образом, детекторная характеристика (2) имеет дискриминантный характер, и поэтому называется также дискриминационной характеристикой (ДХ).
Переходная частота fп и номинальное значение fпр0, а также полосы пропускания ЧД и УПЧ обычно предполагаются равными.
Фильтр нижних частот. Переходные процессы, устойчивость, искажения комплексной огибающей сигнала при функционировании системы ЧАП во многом зависят от свойств и вида фильтра, играющего роль сглаживающей цепи. Именно ФНЧ обеспечивает устойчивость системы, если является единственным инерционным звеном. При использовании системы ЧАП в качестве перестраиваемого фильтра к ее быстродействию предъявляются следующие требования. Плавные, относительно медленные изменения доплеровской частоты принимаемого сигнала в процессе сближения должны по возможности пропускаться ФНЧ без существенных искажений. Высокочастотные составляющие доплеровского сигнала, обусловленные шумом цели, должны подавляться ФНЧ. В данной работе в качестве ФНЧ используется интегратор.
Управляемый генератор описывается регулировочной характеристикойfг (uр), являющейся зависимостью частоты генерируемых колебаний от регулирующего напряжения в статическом режиме. Типовая регулировочная характеристика при использовании системы ЧАП как следящего измерителя скорости показана на рис. 3.

Рис. 3. Регулировочная характеристика управляемого генератора.
Диапазон возможного изменения частоты УГ определяется из соотношения
![]() ,
,
где Fд.min иFд.max– минимальное и максимальное значения доплеровской частоты принимаемого сигнала соответственно. Интервал изменения регулирующего напряжения Δuр определяется особенностями конструктивной реализации УГ. ![]()
Регулировочная характеристика УГ, приведенная на рис. 3, описывается линейной зависимостью
| (3) |
Здесь Sр – крутизна регулировочной характеристики, равная

где Δuр = uр.max – диапазон изменения регулирующего напряжения,uр.max – максимальное значение uр. Заметим, что при таком определении Sр < 0.
Функциональная схема модели системы ЧАП в режиме слежения
Анализ динамического режима работы ЧАП с учетом реальных форм дискриминационной характеристики аналитическими методами имеет серьезные трудности. Поэтому изучение поведения реальных систем ЧАП принято производить на математических моделях, реализуемых на ЭВМ.
В данной работе исследование проводится на основе метода информативного параметра, которым в данном случае является частота. Для этого систему ЧАП представим в виде модели, функциональная схема которой представлена на рис. 4. Модель реализована в среде пакета прикладных программ Simulinkсистемы Matlab.
Скорость протекания переходных процессов в резонансных контурах смесителя, УПЧ, частотного детектора много ниже, чем в фильтре нижних частот. Поэтому соответствующие блоки структурной схемы аппроксимируются безынерционными звеньями, описываемыми статическими характеристиками. При этом в любой момент времени выходной сигнал звена пропорционален входному, а частоты этих сигналов совпадают. Каждое безынерционное звено реализовано в виде блока задания Matlab-функции – частного случая функций, определяемых пользователем [3]. Статические функции (2) и (3), описывающие соответственно ЧД и УГ, заданы выражениями в стиле языка программирования Matlab. УПЧ аппроксимируется безинерционным полосовым фильтром с идеальной прямоугольной АЧХ, симметричной относительно fпр0. При необходимости каждый из перечисленных блоков можно представить динамическим звеном путем некоторого усложнения описания.

Рис. 4. Функциональная схема модели системы ЧАП в режиме слежения.
В схеме рис. 4. использованы следующие обозначения: IFA – усилитель промежуточной частоты, FD – частотный детектор, TG – управляемый генератор. Смеситель моделируется в виде сумматора, осуществляющего операцию вычитания частот по формуле (1). Если требуемое входное воздействие отличается от внутреннего сигнала ППП Simulink, т. е. содержащегося в разделе Sources (Источники сигналов) библиотеки блоков Simulink, то его можно задать с помощью блока FromFile – блока считывания данных из файла *.mat. С помощью источника постоянного сигнала uRICзадается начальное значение регулирующего напряжение uр, используемое для вхождения в режим слежения с заданной доплеровской частотой. Точки возможного съёма информации на схеме представлены выходными портами Outport 1 и 2.
Переходные процессы и стационарный режим системы ЧАП
Для проверки адекватности результатов численного исследования на ЭВМ при тестировании математической модели полезно иметь решение рассматриваемой задачи, полученное каким-либо независимым альтернативным методом. Для этого обычно проводят теоретический анализ процессов в системе ЧАП, доступный при некоторых упрощающих предположениях.
Исследование системы ЧАП аналитическим методом возможно при линеаризации дискриминационной характеристики и простейших тестовых воздействиях. Для этого введем отклонение промежуточной частоты от ее номинального значения fпр0
| (4) |
Эта величина при fп = fпр0имеет смысл ошибки слежения системы ЧАП.
Из (1) следует следующее соотношение при t= 0 и нулевой начальной ошибке слежения:
| (5) |
где fс0 =fс(0), fпр0 = fпр(0), fг0 =fг(0).
Регулировочную характеристику (3) запишем в виде
| (6) |
где fг0 – начальное значение частоты УГ в режиме слежения, δfг – начальная расстройка гетеродина, вызванная его нестабильностью. В формуле (6) учтено, что любое воздействие на частотуfг, отличное от напряжения uр, перемещает регулировочную характеристику вдоль оси частот, вызывая расстройку гетеродина δfг.
Используя (6), вычислим отклонение Δfг частоты гетеродина от ее начального значения fг0:
| (7) |
С учетом (6) рассогласование (4) преобразуем к виду
| (8) |
где δfс = fс – fс0 – отклонение текущей частоты сигнала от начального значения.
Тогда расстройку Δfпр можно выразить через параметры регулировочной характеристики:
| (9) |
Это выражение может применяться для учета вариации как частоты сигнала, так и частоты гетеродина.
Рассмотрим случай, когда нестабильность переходной частоты мала, а fп совпадает с номинальным значением промежуточной частоты fпр0. Кроме того, будем исследовать процессы в системе ЧАП при изменении только частоты fс.
Из рис. 2 видно, что при малых рассогласованиях Δfпр ДХ линейна:
| (10) |
где

– крутизна ДХ в начале координат.
Регулирующее напряжение связано с выходным напряжением ЧД дифференциальным уравнением
|
(11) |
где kи – коэффициент передачи интегратора, p = d/dt– символический оператор дифференцирования.
Соотношения (7),,,(11)представляют собой математическую модель системы ЧАП при малых расстройках. Эту модель можно визуализировать в виде функциональной схемы, показанной на рис. 5.

Рис. 5. Функциональная схема модели системы ЧАП в линейном режиме.
Дифференциальное уравнение, соответствующее схеме рис. 5 и описывающее поведение системы ЧАП при δfг = 0, имеет вид
|
(12) |
В (12) входит постоянная времени системы ЧАП, равная
| (13) |
где Tи =1/ kи – постоянная времени интегратора, kд = Sд kУПЧ, kУПЧ – коэффициент передачи УПЧ. Постоянная времени Tи имеет очевидный физический смысл: если на вход интегратора подать сигнал x = const, то за время, равное Tи, сигнал на его выходе изменится точно на величину x.
Общее решение неоднородного дифференциального уравнения (12) будем искать в виде
| (14) |
г де C1 и C2 – постоянные, определяемые начальными условиями.
Постоянная C1, характеризующая асимптотическое значение расстройки, равна нулю:
![]()
так как апериодический процесс Δfпр(t)→ 0 при t→ ∞. Тогда из (14) следует, что C2 = Δfпр(![]() 0), или, с учетом уравнения рассогласования (8), C2 = – δfг. Здесь принято во внимание, что при безошибочной работе системы ЧАП при t = 0 (момент приложения скачка) расстройка гетеродина Δfг = 0.
0), или, с учетом уравнения рассогласования (8), C2 = – δfг. Здесь принято во внимание, что при безошибочной работе системы ЧАП при t = 0 (момент приложения скачка) расстройка гетеродина Δfг = 0.
Таким образом, общее решение уравнения замкнутой системы ЧАП (14) имеет вид
| (15) |
Формула (15) описывает закон установления ошибки слежения для малых отклонений частоты входного сигнала.
Свойства системы ЧАП как автоматической системы
Важнейшими свойствами системы ЧАП, рассматриваемой как автоматической системы, являются устойчивость, быстродействие и точность действия.
Устойчивостьявляется основным условием работоспособности системы ЧАП. Это связано с тем, что система ЧАП, являясь замкнутой автоматической системой, способна к самовозбуждению. Процесс самовозбуждения начинается со случайного изменения частоты (гетеродина, сигнала или промежуточной), вызывающей появление напряжения на выходе ЧД. Если это напряжение, преобразованное в регулирующее напряжение, поддерживает первоначальное отклонение частоты, то система ЧАП является неустойчивой. Неустойчивость системы проявляется в виде паразитной частотной модуляции сигнала по отношению к изменению частот сигналов, поступающих на их входы.
Неоднородному дифференциальному уравнению (12) соответствует характеристическое уравнение
| (16) |
гдеa0 = t, a1 = 1. Из (16) следует, что в соответствии с критерием Гурвица [4]при малых расстройках и учете инерционности только ФНЧсистема ЧАП устойчива.
Выше предполагалось, что УПЧ и частотный детектор являются безынерционными устройствами. Однако при исследовании устойчивости системы ЧАП необходимо принимать во внимание инерционность указанных устройств. Это вызвано тем, что их инерционность вызывает дополнительные фазовые сдвиги сигнала в контуре обратной связи, которые могут вызвать самовозбуждении системы.
Система ЧАП испытывалась на устойчивость для ФНЧ в виде интегратора и заданных типовых схем построения УПЧ и ЧД. Исследование проводилось в заданной полосе пропускания УПЧ на основе критерия Найквиста [4], который позволяет судить об устойчивости замкнутой линейной системы по виду амплитудно-фазовой характеристики. Для тестирования использовалась функция NyquistППП ControlSystemToolbox[5]. Эта функция предназначена для расчета и построения частотного годографа Найквиста для линейной модели системы с постоянными параметрами. Анализ годографов показывает, что при малых ошибках слежения исследуемая система обеспечивает достаточный запас устойчивость по амплитуде и фазе рассмотренных схем построения в диапазонах изменения параметров, представляющих интерес для практики.
Помимо устойчивости нормально функционирующая автоматическая система должна удовлетворять также определенным требованиям, предъявляемым к качеству ее работы. Функционирование системы ЧАП оценивается показателями качества, характеризующими ее точность действия и быстродействие. Эти показатели, а также запас устойчивости можно определить по переходной характеристике, которая определяется как отклик системы ЧАП на задающее воздействие вида
| (17) |
Быстродействие системы ЧАП определяется по длительности переходного процесса. Величина времени установления tустопределяется как время, прошедшее от момента приложения на вход ступенчатой функции (17) до момента, после которого имеет место неравенство
| (18) |
где Δ – допустимая ошибка вхождения в установившийся режим, представляющая собой заданную малую величину, равную, например, 0,1δfс. Время установления исследуемой системы для данной ошибкиΔс учетом (18) вычисляется по формуле tуст = 2,3t.
График переходного процесса, полученный путем моделирования системы ЧАП (см. рисунки 4 и 5), приведен на рис. 6. До момента t0 = 0,5 с система находилась в режиме слежения, а в момент t0 частота входного сигнала претерпевает скачкообразное изменение (17). Процесс установления ошибки слежения происходит в соответствии с (15)
Из (12) следует, что передаточная функция замкнутой системы ЧАП для ошибки слежения имеет вид
![]()

Рис. 6. Переходной процесс в системе ЧАП при dfс= 200 Гц.
Поэтому при принятых предположениях переходной процесс в системе будет носить апериодический характер [см. также (15)]. Из (13) следует, что постоянная времени системы ЧАП τ в |Sр|kд раз меньше, чем постоянная времени интегратора Tи. Это свидетельствует о более быстром протекании переходных процессов в замкнутой системе, чем в автономном фильтре-интеграторе.
Точность действия системы ЧАП определяется в установившемся режиме. Так как исследуемая система имеет астатизм первого порядка, то статическая ошибка равна нулю (см. рис. 6). Это непосредственно следует и из выражения (15), полученного для ступенчатого воздействия:
![]()
Запас устойчивости оценивается перерегулированием, т. е. относительной величиной отклонения максимальной частоты fпр.maxпереходного процесса от установившегося значения fпр(0):

Считается, что система обладает достаточным запасом устойчивости, если значение σ не превышает 10 …30 % [4]. В исследуемой системе переходной процесс является апериодическим, и σ = 0 %.
Использование системы ЧАП как узкополосного перестраиваемого фильтра
В системах ближней локации (СБЛ) система ЧАП применяется в качестве автоматически перестраиваемого по частоте узкополосного фильтра, осуществляющего частотную селекцию доплеровского сигнала (рис. 7).

Рис. 7. Интерпретация системы ЧАП как следящего фильтра.
В качестве примера, иллюстрирующего особенности изменения доплеровской частоты (ДЧ) во времени в ближней зоне, на рис. 8 приведен график для случая точечной цели [6].
Здесь в качестве параметра используется абсцисса x0 начальной точки – точки на относительной траектории, в момент достижения которой движущейся целью начинается моделирование процессов в ближней зоне.

Рис. 8. Доплеровская частота точечной цели в ближней зоне. Условия встречи: промах – 10 м, относительная скорость – 1000 м/c, диапазон изменения абсциссы x0 – [-40 м, 40 м].
В процессе относительного движения цели ДЧ Fд(t) монотонно убывает в диапазоне от Fд∞ до –Fд∞, где Fд∞ – доплеровская частота “на бесконечности”. Из рис. 8 видно, что на небольшой дальности до цели частота Fд(t) существенно изменяется. В момент пролета, когда на данной траектории расстояние между СБЛ и целью минимально и равно промаху, скорость изменения ДЧ максимальна. Эти особенности динамики ДЧ используются в СБЛ для решения различных задач.
На сравнительно большой дальности при отсутствии маневра взаимодействующих объектов частота Fд(t) мало меняется, и система ЧАП отслеживает эти изменения с небольшой динамической ошибкой. Результаты моделирования показывают, что до тех пор, пока цель, приближаясь к измерителю, находится вне ближней зоны, в системе ЧАП поддерживается режим эффективного слежения, при котором текущая расстройка Dfпр(t)находится в пределах полосы захвата системы ЧАП. Система ЧАП в этом режиме существенно уменьшает ошибку слежения относительно вызвавшего ее приращения доплеровской частоты. Так, например, если абсцисса x0 = 550 м, а приращение Δx= 50 м, то соответствующее изменение доплеровской частоты δFд(Δx) = Fд(x0) – Fд(x0 – Δx) равно –3,2 Гц. Такое приращение ДЧ вызывает расстройку промежуточной частоты Δfпр = –0,3 Гц, так что |Δfпр | << δFд.
Таким образом, в режиме эффективного слежения частота УГ повторяет медленные изменения частоты (Δfг»δfс), вызванные изменением положения цели относительно измерителя. На выходе управляемого генератора формируется сглаженная оценка ДЧ Fд*(t) (с точностью до промежуточной частоты). В этом режиме система ЧАП может быть интерпретирована как узкополосный следящий фильтр, перестраиваемый по частоте почти синхронно с закономерными изменениями доплеровской частоты (см. рис. 7). Полоса пропускания следящего фильтра в основном определяется полосой пропускания УПЧ и остается неизменной во времени.
Для иллюстрации особенностей работы системы ЧАП в ближней зоне рассмотрим рис. 9. Здесь условно принято, что в момент начала моделирования система имеет нулевое рассогласование. При рассмотрении явления срыва слежения следует иметь в виду, что полоса пропускания ЧД равна 8 кГц.
На рис. 9,а показан график доплеровской частоты Fд(t) входного сигнала системы ЧАП. Так как частота УГ fг (t) из-за инерционности ФНЧ запаздывает относительно Fд(t), а скорость изменения ДЧ по мере приближения к точке пролета непрерывно ворастает, то рассогласование Δfпр(t) монотонно увеличивается (рис. 9,б).
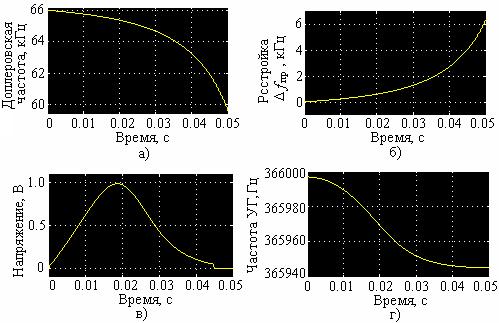
Рис. 9. Результаты моделирования для точечной цели. Условия встречи: промах – 10 м, относительная скорость – 1000 м/c, x0 = 70 м.
Как следует из рис. 2, напряжение на выходе ЧД отлично от нуля, если расстройка ξпринадлежит апертуредискриминатора [–ξm,ξm], где ξm= 4. При больших расстройках, когда |ξ| > ξm, режим слежения прекращается.
Из рис. 9,в видно, что напряжение на выходе ЧД сначала увеличивается (движение по линейному участку правой ветви ДХ), достигает максимума, а затем уменьшается (движение по правому скату ДХ). Отмеченные изменения напряжения происходят при увеличении расстройки Δfпр(t) в процессе сближения в соответствии с формой ДХ. При выходе текущей расстройки Δfпр(t)за пределы апертуры выходное напряжение ЧД становится равным нулю, и регулирующее действие системы ЧАП прекращается. Это эквивалентно размыканию виртуального ключа на выходе ЧД. В этот момент происходит срыв слежения. После срыва слежения напряжение на выходе интегратора, а, следовательно, и частота УГ, сохраняет постоянное значение, достигнутое на момент срыва (рис. 9,г). Заметим также, что ошибка Δfпр(t) после срыва продолжает монотонно увеличиваться (см. рис. 9,б).
В случае протяженной цели характер доплеровского сигнала существенно усложняется [7]. При исследовании СБЛ широкое применение нашли феноменологические модели отражения, основанные на представлении протяженной радиолокационной цели совокупностью конечного числа элементарных отражателей (блестящих точек), определенным образом расположенных на РЛЦ. Каждой блестящей точке приписывается некоторая диаграмма рассеяния. При моделировании комплексная огибающая результирующего эхо-сигнала многоточечной цели представляется в виде векторной суммы огибающих парциальных сигналов.
Для примера на рис. 10 приведены результаты моделирования системы ЧАП при действии эхо-сигнала в случае цели, состоящей из двух блестящих точек. Расстояние между блестящими точки равно 2 м, отношение ЭПР – 1:5. Отрезок прямой, на которой расположены точки, ориентирован параллельно относительной траектории движения. Остальные условия встречи приняты такими же, как для точечной цели (см. рис. 9). Для большей наглядности точки фиксации сигналов и нумерация графиков на рис. 10 такие же, как на рис. 9.
В процессе движения помимо фазовой и амплитудной модуляции парциальных эхо-сигналов, вызванных изменением взаимного положения цели и СБЛ, результирующий сигнал приобретает характер биений, вносящих дополнительную амплитудную и фазовую модуляцию. Биения, порожденные интерференцией парциальных сигналов, в ближней зоне имеют нестационарный колебательный характер с переменными значениями амплитуды и квазипериода. Эта нестационарность обусловлена непрерывным изменением амплитудных и фазовых соотношений принимаемых сигналов в процессе сближения. При неодинаковой интенсивности парциальных колебаний изменение частоты биений во времени характеризуется наличием выбросов (рис. 10,а).
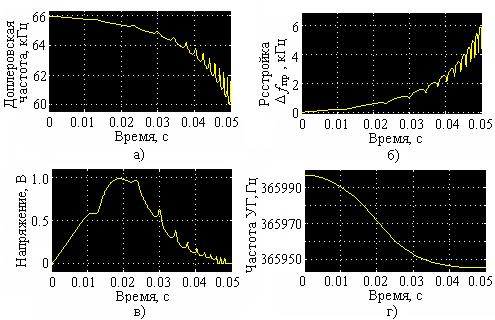
Рис. 10. Результаты моделирования для двухточечной цели.
Таким образом, полученные результаты показывают, что процессы, происходящие в системе ЧАП как до, так и после срыва слежения при работе по протяженной цели носят более сложный характер, чем в случае точечной цели. Это следует учитывать при разработке соответствующих алгоритмов обработки
литература
1. Первачев С.В. Радиавтоматика. М.: Радио и связь. 1982. 296 с.
2. Радиоприемные устройства / Ю.Т. Трифонов, Ю.С. Данич, А.П. Жуковский и др.; Под ред. А.П. Жуковского. М.: Высш. шк. 1989. 342 с.
3. Черных И.В. SIMULINK: среда создания инженерных приложений. М.: Диалог-МИФИ. 2003. 496 с.
4. Радиавтоматика / В.А. Бессекерский, А.А. Елисеев, А В. Небылов и др.; Под ред. В.А. Бессекерского. М.: Высш. шк. 1985. 271 с.
5. Медведев В.С. Потемкин В.Г. Control System Toolbox. М.: Диалог-МИФИ. 1999. 287 с.
6. Об одном алгоритме повышения эффективности. Отчет по теме ”Фундаментальные проблемы создания АИУС”. / МГТУ им.Н. Э. Баумана. Исполнители Ковригин В.А., Герасимов Е.В., Ластовецкий А.Е. ГР.№ 01200964825, M.: 2009. С. 43-51
7. Ковригин В.А. Численное исследование доплеровского сигнала двухточечной цели в ближней зоне // Научный вестник МГТУ ГА. 2010. № 158. С. 60-68.
Публикации с ключевыми словами: автоматическая подстройка частоты, доплеровская частота
Публикации со словами: автоматическая подстройка частоты, доплеровская частота
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||