научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК 519.1
МГТУ им. Н.Э. Баумана
Новые возможности в повышении эффективности обработки информации сопровождаются и появлением новых проблем, преодолеть которые можно на основе достижений в области спектральной теории графов. Пример такой новой проблемы - значительное усложнение задачи эффективного отображения алгоритмов на архитектуру многомодульных параллельных систем. Возникает вопрос о выявлении некоторых дополнительных свойств, присущих алгоритмам, и формулировке соответствующих требований к структурам компьютерных систем (КС).
На основе требований к производительности, отказоустойчивости и точности решения задачи определяются форматы обрабатываемых слов, вычислительная мощность и набор базовых операторов. Путем сравнения вычислительной мощности задачи с вычислительной мощностью типовых процессоров определяется, сколько и какие процессоры требуется иметь в КС для достижения заданной вычислительной мощности, и принимается решение, может ли быть достигнута заданная вычислительная мощность (с учетом имеющейся элементной базы) в рамках однопотоковой, либо многопотоковой организации. Оценивается средняя сложность вычислительной операции и рассчитывается требуемая пропускная способность каналов процессоров для однопотоковой или КС для многопотоковой организации. Определяется требуемая пропускная способность памяти. Зная пропускную способность одного модуля памяти, рассчитывают коэффициент ее распараллеливания. Производится сегментация информационного графа задачи на параллельные ветви по числу модулей памяти и оценивается поток обменов между модулями, определяется характер и объем пересылок между модулями памяти, а также между процессорами. По числу промежуточных результатов определяется объем памяти, ее структура, уточняется число модулей памяти. Оценивается степень загрузки оборудования и необходимый запас вычислительной мощности, пропускная способность каналов, надежность и отказоустойчивость и т. п.
Анализ структурных свойств КС на графе неизбежно приобретает топологический характер - предполагающий использование ряда характеристик, определяющих количественную меру топологии КС [1].
Целесообразность определения таких характеристик состоит в том, что уже на ранней стадии проектирования появляется необходимость оценивать качество структуры КС и ее элементов. Большинство из этих характеристик вычисляется достаточно сложно. Более того, в зависимости от конкретной КС в процессе анализа одинаковые топологические характеристики могут получать различную физическую интерпретацию. Оценим основные топологические характеристики, используемых при анализе КС.
Структурная сложность - определяется как число элементов и связей, составляющих структуру КС. В случае необходимости выделяются элементы, соответствующие изолированным, висячим и тупиковым вершинам графа. Изолированные вершины неинцидентны ни одному из ребер графа, висячие - соответствуют вершинам, в которые нельзя попасть ни из одной другой вершины графа, тупиковые - вершины, из которых нельзя попасть в другие вершины графа. Наличие в графе изолированных вершин обычно свидетельствует об ошибках, допущенных при формировании или описании структуры КС, поскольку вся система - всегда целостный объект [1, 3].
Структурная сложность может быть оценена числом остовных деревьев, содержащихся в графе структуры КС.
Диаметр структуры КС - соответствует метрической характеристике, введенной на графе для определения кратчайшего пути между наиболее удаленными вершинами. По значению диаметра (среднего диаметра) можно косвенно судить о ряде предельных параметров КС, в частности, о ее надежности, длительности задержек сообщений, инерционности, количестве разделяющих вершин и ребер [1].
Структурная связность КС - способность противостоять разбиению, разделению графа структуры КС на независимые части. Данная количественная характеристика позволяет выявить наличие обрывов в топологии, «мосты», и т.д. В теории графов существует несколько определений связности, обусловленных различными критериями. Расчет этих характеристик позволяет оценить структуры КС с разных точек зрения.
Надежность КС - способность структуры КС обеспечить функционирование системы в течение заданного промежутка времени. Надежность является одной из важнейших многопараметрических характеристик структуры и определяется как надежностью элементов, так и схемой объединения элементов.
Живучесть (отказоустойчивость) КС - оценивает сохранение частей структуры КС, обеспечивающих выполнение поставленной задачи. Живучесть имеет тесную функциональную связь с показателями надежности.
Рассмотрим методику определения ряда характеристик, определяющих количественную меру топологии КС.
Сложность КС растет c ростом числа составляющих ее элементов - узлов и ребер. Для связной сети число ребер не может быть меньше числа узлов без единицы, а связные сети максимальной однородности при числе узлов, большем двух, представляют собой кольца с числом узлов, равным числу ребер. Для неориентированной сети в качестве показателя сложности можно использовать показатель однородности ее элементов, определяемый с помощью числовых инвариантов. Сравнивая этот показатель для конкретной сети с заданным числом узлов ![]() и ребер
и ребер ![]() с показателем максимально однородной сети с таким же числом элементов, можно определить, насколько данная сеть отличается от наименее сложной. Сложность сети зависит не только от числа элементов, но и от их взаимосвязи, которое можно охарактеризовать через разность числа ребер и числа узлов
с показателем максимально однородной сети с таким же числом элементов, можно определить, насколько данная сеть отличается от наименее сложной. Сложность сети зависит не только от числа элементов, но и от их взаимосвязи, которое можно охарактеризовать через разность числа ребер и числа узлов ![]() .
.
Сложность графа структуры КС можно оценивать числом ![]() , которое связано с коэффициентами многочлена
, которое связано с коэффициентами многочлена ![]()
![]()
выраженного в терминах «древовидной» структуры мультиграфа ![]() . Если
. Если ![]() - мультиграф с вершинами
- мультиграф с вершинами ![]() и
и ![]() обозначает число остовных деревьев, содержащихся в
обозначает число остовных деревьев, содержащихся в ![]() , то
, то
![]()
где ![]() - матрица полных проводимостей графа
- матрица полных проводимостей графа ![]() , a
, a ![]() [1, 3].
[1, 3].
Если ![]() , то
, то
![]()
Отсюда следует что, если
![]()
где ![]() - произвольный мультиграф, а
- произвольный мультиграф, а ![]() - его матрица полных проводимостей. Тогда
- его матрица полных проводимостей. Тогда
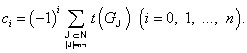 (1)
(1)
При ![]() из уравнения (1) следует
из уравнения (1) следует
![]()
Следовательно,
(i) ![]()
Пусть ![]() (в некоторой последовательности) - собственные значения матрицы
(в некоторой последовательности) - собственные значения матрицы ![]() . Так как
. Так как ![]() , то отсюда следует, что
, то отсюда следует, что ![]() . Пусть, далее
. Пусть, далее ![]() . Тогда
. Тогда ![]() и из (i) получаем
и из (i) получаем
(ii) ![]()
Если граф ![]() связен, то
связен, то ![]() , т.е.
, т.е. ![]() для
для ![]() . Этим результатом доказано, что если
. Этим результатом доказано, что если ![]() - связный мультиграф, то
- связный мультиграф, то
![]()
причем ![]() пробегает все отличные от нуля собственные значения матрицы
пробегает все отличные от нуля собственные значения матрицы ![]() .
.
Для любого регулярного мультиграфа ![]() степени
степени ![]()
![]()
где ![]() - обыкновенные собственные значения мультиграфа
- обыкновенные собственные значения мультиграфа ![]() .
.
Пусть ![]() - мультиграф, содержащий n вершин с положительными валентностями
- мультиграф, содержащий n вершин с положительными валентностями ![]() . Тогда сложность графа
. Тогда сложность графа ![]() может быть определена по формуле
может быть определена по формуле
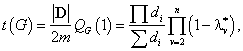
где ![]() и
и ![]() соответственно число ребер и
соответственно число ребер и ![]() -собственное значение графа
-собственное значение графа ![]() .
.
Пропускная способность вычислительной системы определяется максимальным потоком сообщений, который может быть организован между ее узлами. Можно показать, что при равной пропускной способности узлов и ребер (узлов коммутации сообщений и линий связи) пропускная способность сети обратно пропорциональна среднему расстоянию между ее узлами.
Пусть ![]() - связный граф, вершины которого перенумерованы числами
- связный граф, вершины которого перенумерованы числами ![]() . Расстояние
. Расстояние ![]() между вершинами
между вершинами ![]() и
и ![]() в
в ![]() , как обычно, определяется минимальным числом ребер в любой из простых цепей между
, как обычно, определяется минимальным числом ребер в любой из простых цепей между ![]() и
и ![]() . Матрица
. Матрица ![]() называется матрицей расстояний графа
называется матрицей расстояний графа ![]() , а соответствующий характеристический многочлен - характеристическим многочленом матрицы расстояний графа
, а соответствующий характеристический многочлен - характеристическим многочленом матрицы расстояний графа ![]() .
.
Общая формула характеристического многочлена матрицы расстояний простой цепи, а также таблицы характеристических многочленов матриц расстояний некоторых графов приведены ниже. Установлено, что определитель матрицы расстояний дерева зависит лишь от числа вершин, т.е. не зависит от структуры дерева. Для дерева ![]() с
с ![]() вершинами имеем
вершинами имеем
![]() (2)
(2)
Характеристические многочлены матриц расстояний связываются со следующей задачей вложения.
Пусть ![]() , а
, а ![]() - функция из
- функция из ![]() в множество неотрицательных целых чисел, определенная посредством соотношений
в множество неотрицательных целых чисел, определенная посредством соотношений
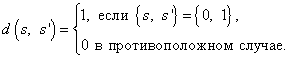
Эта функция может быть продолжена до отображения произведения ![]() в множество неотрицательных целых чисел следующим образом:
в множество неотрицательных целых чисел следующим образом:
![]()
Задача состоит в том, чтобы для заданного связного графа ![]() найти наименьшее целое число
найти наименьшее целое число ![]() , для которого существует отображение
, для которого существует отображение ![]() из множества вершин графа
из множества вершин графа ![]() в
в ![]() такое, что
такое, что ![]() для всех пар вершин
для всех пар вершин ![]() и
и ![]() в
в ![]() . Получен следующий результат.
. Получен следующий результат.
Пусть ![]() и
и ![]() - числа положительных и отрицательных собственных значений матрицы расстояний
- числа положительных и отрицательных собственных значений матрицы расстояний ![]() для графа
для графа ![]() . Тогда
. Тогда ![]() . Кроме того, число
. Кроме того, число ![]() определено для полных графов, простых циклов и деревьев.
определено для полных графов, простых циклов и деревьев.
Определитель матрицы расстояний любого сильно связного орграфа ![]() зависит лишь от блоков (две дуги орграфа считаются принадлежащими одному и тому же блоку тогда и только тогда, когда в орграфе существует контур, содержащий обе дуги) орграфа
зависит лишь от блоков (две дуги орграфа считаются принадлежащими одному и тому же блоку тогда и только тогда, когда в орграфе существует контур, содержащий обе дуги) орграфа ![]() и не зависит от того, как эти блоки связаны между собой. Получены следующие формулы:
и не зависит от того, как эти блоки связаны между собой. Получены следующие формулы:
 (3)
(3)
где ![]() - блоки орграфа
- блоки орграфа ![]() , a
, a![]() означает (для любой квадратной матрицы
означает (для любой квадратной матрицы ![]() сумму алгебраических дополнений матрицы
сумму алгебраических дополнений матрицы ![]() . Формулы (3) являются обобщением формулы (2). В этом легко убедиться, если заменить в дереве каждое ребро двумя ориентированными ребрами взаимно противоположной направленности и затем применить (3) к полученному орграфу.
. Формулы (3) являются обобщением формулы (2). В этом легко убедиться, если заменить в дереве каждое ребро двумя ориентированными ребрами взаимно противоположной направленности и затем применить (3) к полученному орграфу.
Были исследованы другие обобщения формулы (2) коэффициенты ![]() характеристического многочлена матрицы расстояний дерева (напомним, что
характеристического многочлена матрицы расстояний дерева (напомним, что ![]() . Доказано [3], что
. Доказано [3], что
![]()
где ![]() - число порожденных графов, изоморфных
- число порожденных графов, изоморфных ![]() и содержащихся в рассматриваемом дереве. В этой работе приведены также соответствующие выражения для коэффициентов
и содержащихся в рассматриваемом дереве. В этой работе приведены также соответствующие выражения для коэффициентов ![]() и
и ![]() и сформулировано утверждение относительно общего вида коэффициентов характеристического многочлена матрицы расстояний. Это утверждение, состоящее в том, что
и сформулировано утверждение относительно общего вида коэффициентов характеристического многочлена матрицы расстояний. Это утверждение, состоящее в том, что ![]() может быть выражено через линейную комбинацию чисел
может быть выражено через линейную комбинацию чисел ![]() для различных
для различных ![]() .
.
Вопрос в том, определяется ли граф однозначно характеристическим многочленом матрицы расстояний.
Если ![]() - метрически регулярный граф с матрицами смежности порожденной ассоциативной схемы
- метрически регулярный граф с матрицами смежности порожденной ассоциативной схемы ![]() , то очевидно, что
, то очевидно, что
![]()
Так как матрица смежности ![]() графа является симметрической, можно на основе спектра определить ее минимальный многочлен. Если, как известно,
графа является симметрической, можно на основе спектра определить ее минимальный многочлен. Если, как известно, ![]() множество всех различных собственных значений матрицы
множество всех различных собственных значений матрицы ![]() , то соответствующий минимальный многочлен
, то соответствующий минимальный многочлен
![]()
Пусть ![]() Тогда справедливо соотношение
Тогда справедливо соотношение
![]() (4)
(4)
Используя выражение (4), можно утверждать, что если связный граф ![]() имеет точно
имеет точно ![]() различных собственных значений, то его диаметр
различных собственных значений, то его диаметр ![]() удовлетворяет неравенству
удовлетворяет неравенству ![]() .
.
Для развития средств вычислительной техники необходимо решить в первую очередь вопрос об эффективности их функционирования и достоверности получаемых с их помощью результатов. Непосредственное использование ЦВМ и многопроцессорных КС в системах управления космическими аппаратами и средств выведения еще более обострило вопрос о надежности функционирования и живучести средств вычислительной техники. В последнее время остро встала задача разработки концепции отказоустойчивых систем, а также сделаны попытки построить первые КС повышенной живучести.
Живучесть (отказоустойчивость) - это свойство системы адаптироваться к новой ситуации и противостоять «разрушительным» воздействиям, выполняя при этом свою целевую функцию за счет соответствующего изменения структуры и поведения КС даже при отказе определенной части входящих в нее модулей [1].
Живучесть КС можно рассчитать, используя понятие алгебраической связности графа вычислительной системы. ![]() -спектр
-спектр ![]() графа
графа ![]() определяется как спектр матрицы
определяется как спектр матрицы ![]() . Матрицу
. Матрицу ![]() можно представить в виде
можно представить в виде ![]() , где
, где ![]() - вершинно-реберная матрица
- вершинно-реберная матрица ![]() -инциденций орграфа, полученного из
-инциденций орграфа, полученного из ![]() ориентированием каждого ребра графа
ориентированием каждого ребра графа ![]() произвольным образом. Следовательно,
произвольным образом. Следовательно, ![]() - симметрическая особенная (так как все суммы элементов строк равны нулю) и положительно полуопределенная матрица, т.е. ее собственные значения неотрицательны и наименьшее из них всегда равно нулю. Второе минимальное
- симметрическая особенная (так как все суммы элементов строк равны нулю) и положительно полуопределенная матрица, т.е. ее собственные значения неотрицательны и наименьшее из них всегда равно нулю. Второе минимальное ![]() -собственное значение
-собственное значение ![]() будем обозначать через
будем обозначать через ![]() . Эта величина во многом определяет свойства вершинной или реберной связности (граф
. Эта величина во многом определяет свойства вершинной или реберной связности (граф ![]()
![]() -вершинно (реберно) связен, если
-вершинно (реберно) связен, если ![]() - наименьшее число вершин (ребер), при удалении которых граф становится несвязным или состоит из изолированной вершины) и называется алгебраической связностью графа. Опишем ее некоторые свойства [1, 2].
- наименьшее число вершин (ребер), при удалении которых граф становится несвязным или состоит из изолированной вершины) и называется алгебраической связностью графа. Опишем ее некоторые свойства [1, 2].
Матрица ![]() неотрицательна и имеет одинаковые строчные суммы. Следовательно, кратность наибольшего собственного значения равна числу компонент графа
неотрицательна и имеет одинаковые строчные суммы. Следовательно, кратность наибольшего собственного значения равна числу компонент графа ![]() . Это означает, что
. Это означает, что ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() несвязен.
несвязен.
Если ![]() - непересекающиеся по ребрам графы на одном и том же множестве вершин, то
- непересекающиеся по ребрам графы на одном и том же множестве вершин, то ![]() Другими словами, введение в граф новых ребер не уменьшает алгебраической связности. Чтобы доказать это свойство, рассмотрим множество W n-мерных векторов, в которых сумма координат равна нулю. Имеем
Другими словами, введение в граф новых ребер не уменьшает алгебраической связности. Чтобы доказать это свойство, рассмотрим множество W n-мерных векторов, в которых сумма координат равна нулю. Имеем
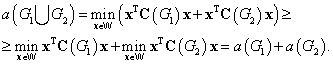
Легко убедиться в том, что ![]() - собственное значение матрицы
- собственное значение матрицы ![]() где
где ![]() - любой граф на
- любой граф на ![]() вершинах. Если
вершинах. Если ![]() - порожденный подграф графа
- порожденный подграф графа ![]() на
на ![]() вершинах, то
вершинах, то ![]() можно рассматривать как остовный подграф графа
можно рассматривать как остовный подграф графа ![]() для некоторого
для некоторого ![]() . Поэтому
. Поэтому ![]() Предположим далее, что
Предположим далее, что ![]() имеет вершинную связность
имеет вершинную связность ![]() и
и ![]() - множество разреза (множество вершин (ребер), в результате удаления которых граф становится несвязным, называется множеством разреза) для
- множество разреза (множество вершин (ребер), в результате удаления которых граф становится несвязным, называется множеством разреза) для ![]() . Тогда
. Тогда ![]() несвязен,
несвязен, ![]() и
и ![]() , кроме того, используя неравенство
, кроме того, используя неравенство ![]() где
где ![]() - реберная связность графа
- реберная связность графа ![]() , можно найти способ построения множества разреза в графе
, можно найти способ построения множества разреза в графе ![]() с помощью собственного вектора матрицы
с помощью собственного вектора матрицы ![]() , соответствующего
, соответствующего ![]() .
.
Если наряду со спектром графа ![]() известны также собственные векторы матрицы
известны также собственные векторы матрицы ![]() , то, разумеется, о структуре графа
, то, разумеется, о структуре графа ![]() можно утверждать больше, чем, если бы этой информации не было. Более того, мультиорграф
можно утверждать больше, чем, если бы этой информации не было. Более того, мультиорграф ![]() с симметрической матрицей смежности, в частности мультиграф, полностью определяется собственными значениями и собственными векторами. Так, если
с симметрической матрицей смежности, в частности мультиграф, полностью определяется собственными значениями и собственными векторами. Так, если ![]() полная система взаимно ортогональных нормированных собственных векторов матрицы
полная система взаимно ортогональных нормированных собственных векторов матрицы ![]() , соответствующих спектру
, соответствующих спектру ![]() и
и ![]() то, как известно [2],
то, как известно [2], ![]() - ортогональная матрица (т.е.
- ортогональная матрица (т.е. ![]() и
и
![]() . (4)
. (4)
Поскольку граф ![]() определяется матрицей
определяется матрицей ![]() , то мультиграф полностью определяется собственными значениями и собственными векторами.
, то мультиграф полностью определяется собственными значениями и собственными векторами.
Таким образом, любую задачу для мультиграфа можно рассматривать в терминах спектров и собственных векторов. Исследуем с этой точки зрения задачу о числе маршрутов данной длины в мультиграфе (мультиорграфе) ![]() . (Напомним: маршрут длины
. (Напомним: маршрут длины ![]() - это последовательность дуг
- это последовательность дуг ![]() , в которой начальная вершина дуги
, в которой начальная вершина дуги ![]() совпадает с концевой вершиной дуги
совпадает с концевой вершиной дуги ![]() ,
, ![]() , при этом допускаются повторения и петли.) Пусть
, при этом допускаются повторения и петли.) Пусть ![]() - матрица смежности мультиорграфа
- матрица смежности мультиорграфа ![]() с вершинами
с вершинами ![]() и
и ![]() пусть, далее,
пусть, далее, ![]() означает число маршрутов длины
означает число маршрутов длины ![]() , начинающихся в вершине
, начинающихся в вершине ![]() и оканчивающихся в вершине
и оканчивающихся в вершине ![]() . Тогда
. Тогда
![]() (5)
(5)
Заметим, что для ![]() (5) согласуется с обозначением
(5) согласуется с обозначением ![]() .
.
Пусть теперь ![]() означает мультиграф и
означает мультиграф и ![]() - ортогональная матрица собственных векторов матрицы
- ортогональная матрица собственных векторов матрицы ![]() , как описано выше. Тогда согласно (4)
, как описано выше. Тогда согласно (4)
![]() (6)
(6)
и число всех маршрутов длины ![]() в графе
в графе ![]() будет составлять
будет составлять
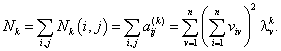
Таким образом, общее число маршрутов длины ![]() в мультиграфе
в мультиграфе ![]()
![]() (7)
(7)
где 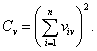
Представим производящую функцию чисел ![]() в терминах характеристических многочленов графа
в терминах характеристических многочленов графа ![]() и его дополнения
и его дополнения ![]() . Пусть
. Пусть ![]() - граф с дополнением
- граф с дополнением ![]() и
и ![]() - производящая функция чисел
- производящая функция чисел ![]() маршрутов длины
маршрутов длины ![]() в графе
в графе ![]()
![]() . Тогда
. Тогда
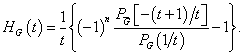 (8)
(8)
Пусть ![]() - невырожденная квадратная матрица порядка
- невырожденная квадратная матрица порядка ![]() ,
, ![]() - матрица, образованная минорами порядка
- матрица, образованная минорами порядка ![]() так, что
так, что ![]() . Пусть, далее,
. Пусть, далее, ![]() означает сумму всех элементов матрицы
означает сумму всех элементов матрицы ![]() и
и ![]() - квадратная матрица, значения всех элементов которой равны 1. Тогда для произвольного числа
- квадратная матрица, значения всех элементов которой равны 1. Тогда для произвольного числа ![]()
![]() , (9)
, (9)
что может быть доказано непосредственными вычислениями. С учетом выражения (5) ![]() и, поскольку
и, поскольку
![]()
получаем
![]()
т.e.
![]() (10)
(10)
Из равенства (9), полагая ![]() и х = t, находим
и х = t, находим
![]() (11)
(11)
где ![]() матрица смежности дополнения
матрица смежности дополнения ![]() графа G; подставляя (11) в (10), получаем
графа G; подставляя (11) в (10), получаем
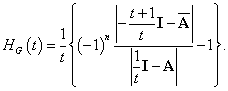 (12)
(12)
А из (12) следует (8) доказывает формулу производящей функции чисел ![]() [3].
[3].
Итак, число маршрутов в графе связано с его спектром. Производящая функция ![]() для числа маршрутов определяется через характеристические многочлены графа и его дополнения.
для числа маршрутов определяется через характеристические многочлены графа и его дополнения.
Например, регулярный граф степени ![]() с
с ![]() вершинами имеет, очевидно,
вершинами имеет, очевидно, ![]() путей длины
путей длины ![]() и, следовательно,
и, следовательно,
![]()
При ![]() получаются полные графы, а при
получаются полные графы, а при ![]() - графы, состоящие лишь из изолированных вершин. Для графа, который имеет только одну вершину и не имеет ребер и петель, производящая функция имеет вид
- графы, состоящие лишь из изолированных вершин. Для графа, который имеет только одну вершину и не имеет ребер и петель, производящая функция имеет вид ![]() .
.
Определим число маршрутов длины ![]() в простой цепи
в простой цепи ![]() с
с ![]() вершинами. Матрица смежности цепи
вершинами. Матрица смежности цепи ![]() такова:
такова:
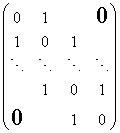 .
.
Собственными значениями такой матрицы являются ![]()
![]() . Легко убедиться в том, что
. Легко убедиться в том, что ![]() являются координатами нормализованного собственного вектора
являются координатами нормализованного собственного вектора ![]() , соответствующего собственному значению
, соответствующего собственному значению ![]() . Используя (7), для числа
. Используя (7), для числа ![]() маршрутов длины
маршрутов длины ![]() в
в ![]() получаем выражение
получаем выражение
![]() (13)
(13)
Этот результат может быть использован для нахождения числа ![]() маршрутов длины
маршрутов длины ![]() в различных графах структур КС.
в различных графах структур КС.
Таким образом, приведенные процедуры выбора топологии структуры КС по критериям сложность, производительность, отказоустойчивость и оценки числа маршрутов в графах структур КС, базируются на спектральной теории графов. Рассмотренные соотношения позволяют сделать заключение о пригодности той или иной вычислительной структуры для решения конкретных задач.
СПИСОК ЛИТЕРАТУРЫ
1. Андреев А. М., Можаров Г. П., Сюзев В. В. Многопроцессорные вычислительные системы: теоретический анализ, математические модели и применение: учеб. пособие / - М.: Изд-во МГТУ им. Н. Э. Баумана, 2011. - 334 с.
2. Хорн Р., Джонсон Ч. Матричный анализ. Пер. с англ. - М.: Мир, 1989. - 655 с.
3. Cvetkovic D., Rowlinson P., Simic S. Eigenspaces of graphs. Cambridge University Press, 1997. - 260 р.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



