научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК 51.519.2
МГТУ им. Н.Э. Баумана
1. Введение
Дисперсионный анализ определяется как статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, в связи, с чем область применения этого метода становится значительно шире. Несмещенной оценкой для неизвестных параметром является, как известно, сумма квадратов. Основная идея дисперсионного анализа заключается в разбиении этой суммы квадратов отклонений на несколько компонент, каждая из которых соответствует предполагаемой причине изменения средних ([1], гл. 3, п. 3.1.3. с. 92).
Рассмотрим разложение остаточной суммы квадратов
![]()
и докажем независимость слагаемых ![]() и
и ![]() . Для доказательства нам понадобятся две теоремы и четыре вспомогательные леммы.
. Для доказательства нам понадобятся две теоремы и четыре вспомогательные леммы.
Лемма 1.1. Ранг произведения двух матриц ![]() и
и ![]() меньше или равен минимального из рангов матриц
меньше или равен минимального из рангов матриц ![]() и
и ![]() , т.е.
, т.е.
![]()
Доказательство. Так как по правилу умножения матриц столбцы матрицы ![]() являются линейной комбинацией столбцов матрицы
являются линейной комбинацией столбцов матрицы ![]() , то число линейно независимых столбцов в
, то число линейно независимых столбцов в ![]() не может превосходить число линейно независимых столбцов в
не может превосходить число линейно независимых столбцов в ![]() ; следовательно,
; следовательно, ![]() . Проведя аналогичные рассуждения для строк (строки
. Проведя аналогичные рассуждения для строк (строки ![]() являются линейной комбинацией строк
являются линейной комбинацией строк ![]() ), получим, что
), получим, что ![]() . Лемма доказана.
. Лемма доказана.
Следствие закона инерции квадратичных форм (о количестве инвариантов): если ![]() является квадратичной формой от
является квадратичной формой от ![]() переменных
переменных ![]() и ее ранг равен
и ее ранг равен ![]() , т.е.
, т.е. ![]() , то существует
, то существует ![]() линейных комбинаций переменных
линейных комбинаций переменных ![]() , например,
, например, ![]() , таких, что
, таких, что ![]() и каждое
и каждое ![]() или
или ![]() .
.
Используем теорему Кохрана [1], как простое следствие следующей теоремы.
Теорема 1.1. Пусть ![]() , где
, где ![]() является квадратичной формой ранга
является квадратичной формой ранга ![]() от переменных
от переменных ![]() . Тогда необходимым и достаточным условием существования ортогонального преобразования
. Тогда необходимым и достаточным условием существования ортогонального преобразования ![]() , переводящего вектор
, переводящего вектор ![]() в вектор
в вектор ![]() так, чтобы при этом
так, чтобы при этом
![]() (1.1)
(1.1)
является условие ![]() .
.
Доказательство. Необходимость. Если такое ортогональное преобразование существует, то  . Левая часть является квадратичной формой ранга
. Левая часть является квадратичной формой ранга ![]() , а правая часть – квадратичной формой ранга
, а правая часть – квадратичной формой ранга ![]() . По лемме 1.2 отсюда следует, что ранги квадратичных форм равны, т.е.
. По лемме 1.2 отсюда следует, что ранги квадратичных форм равны, т.е. ![]() .
.
Достаточность. Так как ранг ![]() равен
равен ![]() , то из следствия закона инерции квадратичных форм отсюда следует, что существует
, то из следствия закона инерции квадратичных форм отсюда следует, что существует ![]() линейных комбинаций
линейных комбинаций ![]() переменных
переменных ![]() , таких, что
, таких, что ![]() , где каждое
, где каждое ![]() или
или ![]() . Для
. Для ![]() индексы
индексы ![]() принимают значения
принимают значения ![]() ; для
; для ![]() –
– ![]() и т.д. Теперь, если
и т.д. Теперь, если ![]() , то существует
, то существует ![]() линейных комбинаций
линейных комбинаций ![]() , которые в матричных обозначениях можно записать так:
, которые в матричных обозначениях можно записать так: ![]() .
.
Вводя диагональную матрицу ![]() с диагональными элементами
с диагональными элементами ![]() , получаем, что
, получаем, что  . С другой стороны,
. С другой стороны,  . Так как симметричная матрица квадратичной формы единственна, то заключаем, что
. Так как симметричная матрица квадратичной формы единственна, то заключаем, что ![]() , следовательно,
, следовательно, ![]() невырождена. Теперь докажем, что
невырождена. Теперь докажем, что ![]() . Действительно, предположим, что
. Действительно, предположим, что ![]() . Тогда по формуле
. Тогда по формуле ![]() мы можем найти значения
мы можем найти значения ![]() , соответствующие значениям
, соответствующие значениям ![]() при
при ![]() и
и ![]() , а для этих значений
, а для этих значений ![]() , что невозможно. Следовательно,
, что невозможно. Следовательно, ![]() и
и ![]() . Последнее равенство показывает, что преобразование
. Последнее равенство показывает, что преобразование ![]() ортогонально. Теорема доказана.
ортогонально. Теорема доказана.
Замечание. Условие ![]() обеспечивает всем квадратичным формам
обеспечивает всем квадратичным формам ![]() положительную определенность, так как при ортогональном преобразовании получается, что все их характеристические числа равны 0 или 1.
положительную определенность, так как при ортогональном преобразовании получается, что все их характеристические числа равны 0 или 1.
Теорема 1.2 [1]. Пусть случайные величины ![]() независимы и имеют нормальные распределения
независимы и имеют нормальные распределения ![]() соответственно. Пусть далее
соответственно. Пусть далее
![]() ,
,
где ![]() – квадратичная форма от переменных
– квадратичная форма от переменных ![]() ранга
ранга ![]() . Тогда
. Тогда ![]() будут иметь независимые нецентральные
будут иметь независимые нецентральные ![]() -распределения с
-распределения с ![]() степенями свободы соответственно тогда и только тогда, когда
степенями свободы соответственно тогда и только тогда, когда ![]() . Если через
. Если через ![]() обозначен параметр нецентральности
обозначен параметр нецентральности ![]() , то значение
, то значение ![]() может быть получено заменой
может быть получено заменой ![]() на
на ![]() в
в ![]() , т.е. если
, т.е. если ![]() , то
, то ![]() , где
, где ![]() ;
; ![]() .
.
Доказательство. Необходимость. Если ![]() являются независимыми случайными величинами, имеющими
являются независимыми случайными величинами, имеющими ![]() -распределения с
-распределения с ![]() степенями свободы соответственно, то из определения нецентрального
степенями свободы соответственно, то из определения нецентрального ![]() -распределения следует, что
-распределения следует, что ![]() имеет нецентральное
имеет нецентральное ![]() -распределение с
-распределение с ![]() степенями свободы. Но так как
степенями свободы. Но так как ![]() имеет нецентральное
имеет нецентральное ![]() -распределение с
-распределение с ![]() степенями свободы, а
степенями свободы, а  , то, следовательно,
, то, следовательно, 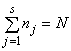 .
.
Достаточность. Пусть 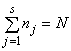 . Тогда при ортогональном преобразовании
. Тогда при ортогональном преобразовании ![]() теоремы 1.1, случайные величины
теоремы 1.1, случайные величины ![]() снова будут независимыми и нормально распределенными. Из соотношений (1.1) и определения нецентрального
снова будут независимыми и нормально распределенными. Из соотношений (1.1) и определения нецентрального ![]() -распределения следует, что
-распределения следует, что ![]() имеют независимые нецентральные
имеют независимые нецентральные ![]() -распределения с
-распределения с ![]() степенями свободы соответственно. Теорема доказана.
степенями свободы соответственно. Теорема доказана.
2. Вспомогательные теоремы и леммы
Предположим, что пространство значений случайных величин разбито на конечное число r частей ![]() без общих точек, и пусть
без общих точек, и пусть ![]() - соответствующие вероятности
- соответствующие вероятности ![]() ,
, ![]() .
.
Будем предполагать, что все ![]() . Обозначим через
. Обозначим через ![]() число наблюденных значений случайных величин – X принадлежащих множеству
число наблюденных значений случайных величин – X принадлежащих множеству ![]() .
.
Рассмотрим вектор (![]() ). В качестве меры расхождения между эмпирическим и теоретическим распределением рассмотрим выражение
). В качестве меры расхождения между эмпирическим и теоретическим распределением рассмотрим выражение ![]() , где коэффиценты
, где коэффиценты ![]() могут быть выбраны более или менее произвольно. Пирсон показал ([2] гл.10.6, с.261, [3] , что если
могут быть выбраны более или менее произвольно. Пирсон показал ([2] гл.10.6, с.261, [3] , что если ![]() , то полученная мера
, то полученная мера
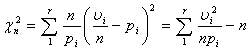 (2.1)
(2.1)
обладает чрезвычайно простыми свойствами.
Теорема 2.1. При ![]() распределение
распределение ![]() стремится к распределению
стремится к распределению ![]() с r – 1 степенями свободы.
с r – 1 степенями свободы.
На основании этой теоремы по заданному уровню значимости a находят по таблицам число ![]() из условия
из условия
![]() (2.2)
(2.2)
Гипотеза ![]() отвергается, если вычисленная по выборке величина
отвергается, если вычисленная по выборке величина ![]() .
.
При доказательстве теоремы нам потребуется следующая лемма.
Лемма 2.1. Пусть ![]() - целые неотрицательные числа, причем
- целые неотрицательные числа, причем ![]() . Число способов, посредством которых n элементов могут разделены на r групп, из которых первая содержит
. Число способов, посредством которых n элементов могут разделены на r групп, из которых первая содержит ![]() элементов, вторая
элементов, вторая ![]() элементов, …,
элементов, …, ![]() элементов равно
элементов равно ![]() .
.
Доказательство. Первую группу из ![]() элементов можно выбрать
элементов можно выбрать ![]() способами. После того, как образована первая группа, остается n -
способами. После того, как образована первая группа, остается n - ![]() элементов. Поэтому вторую группу из
элементов. Поэтому вторую группу из ![]() элементов можно выбрать
элементов можно выбрать ![]() способами и.т.д. После образования r – 1 группы остается
способами и.т.д. После образования r – 1 группы остается ![]() элементов, которые и образуют последнюю группу. Таким образом, число всех возможных способов, посредством которых n элементов могут быть распределены на r групп, из которых первая содержит
элементов, которые и образуют последнюю группу. Таким образом, число всех возможных способов, посредством которых n элементов могут быть распределены на r групп, из которых первая содержит ![]() элементов, … ,
элементов, … , ![]() содержит
содержит ![]() элементов, равно
элементов, равно
![]() .
.
Используя формулу  , получим утверждение леммы.
, получим утверждение леммы.
Доказательство. Результат любого испытания с вероятностью ![]() будет принадлежать множеству
будет принадлежать множеству ![]() . Поэтому, на основании леммы 2.1, вероятность того, что в процессе n независимых испытаний
. Поэтому, на основании леммы 2.1, вероятность того, что в процессе n независимых испытаний ![]() значений будет принадлежать множеству
значений будет принадлежать множеству ![]() , … ,
, … , ![]() значений будет принадлежать множеству
значений будет принадлежать множеству ![]() , равно
, равно
![]() (2.3)
(2.3)
Это выражение, как легко видеть, является общим членом разложения ![]() . Совместное распределение случайного вектора
. Совместное распределение случайного вектора ![]() задается (2.3) и является полиноминальным распределением. Найдем характеристическую функцию с полиноминальным распределением. Имеем
задается (2.3) и является полиноминальным распределением. Найдем характеристическую функцию с полиноминальным распределением. Имеем

Введем новые величины ![]() ,
, ![]() . Тогда, очевидно,
. Тогда, очевидно, ![]() ,
, ![]() . Найдем характеристическую функцию случайного вектора
. Найдем характеристическую функцию случайного вектора ![]() . Имеем
. Имеем
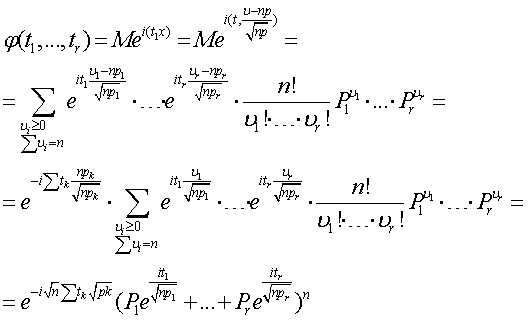 (2.4)
(2.4)
Далее, для любых фиксированных ![]() получим
получим
![]() (2.5)
(2.5)
Из разложений ![]() ,
, ![]() ,
, ![]() и из (2.6) следует
и из (2.6) следует

 (2.6)
(2.6)
Таким образом, из (2.6) получаем
 (2.7)
(2.7)
Квадратичная форма ![]() имеет матрицу
имеет матрицу ![]() , где Iобозначает единичную матрицу, а P – вектор – столбец, заменяя
, где Iобозначает единичную матрицу, а P – вектор – столбец, заменяя ![]() новыми переменными
новыми переменными ![]() с помощью ортогонального преобразования, при котором
с помощью ортогонального преобразования, при котором ![]() , получим
, получим ![]() .
.
Итак, квадратичная форма ![]() неотрицательная и имеет ранг r – 1 , т.е. при
неотрицательная и имеет ранг r – 1 , т.е. при ![]() совместная характеристическая функция величин
совместная характеристическая функция величин ![]() стремится к выражению
стремится к выражению ![]() , являющемуся характеристической функцией некоторого несобственного нормального распределения ранга r – 1 , в котором вся масса сосредоточена на гиперплоскости
, являющемуся характеристической функцией некоторого несобственного нормального распределения ранга r – 1 , в котором вся масса сосредоточена на гиперплоскости ![]() .
.
Из теоремы непрерывности следует, что в пределе величины ![]() имеют несобственное нормальное распределение с нулевыми, средними и матрицей вторых моментов
имеют несобственное нормальное распределение с нулевыми, средними и матрицей вторых моментов ![]() . Отсюда получаем, что в пределе величина
. Отсюда получаем, что в пределе величина ![]() имеет распределение
имеет распределение ![]() степенями свободы, ч.т.д.
степенями свободы, ч.т.д.
3. Нецентральное хи-квадрат распределение
Рассмотрим случай, когда у1, у2,…, уn — независимые случайные величины, имеющие нормальное распределение со средним ![]() (i=1, 2,…,n) и дисперсией 1, т. е.
(i=1, 2,…,n) и дисперсией 1, т. е.
![]() ~N (
~N (![]() ) (i=1, 2,…,n). Тогда распределение случайной величины
) (i=1, 2,…,n). Тогда распределение случайной величины
![]()
называется нецентральным ![]() -распределением [1-3].
-распределением [1-3].
Величина ![]() представляет собой радиус гиперсферы в n-мерном пространстве [1,4].
представляет собой радиус гиперсферы в n-мерном пространстве [1,4].
Распределение случайной величины u зависит только от параметров nи  . Поэтому его также называют нецентральным
. Поэтому его также называют нецентральным ![]() -распределением с n степенями свободы и параметром нецентральности
-распределением с n степенями свободы и параметром нецентральности ![]() [2,5,6]. В этом случае, следуя [4], случайную величину u будем обозначать
[2,5,6]. В этом случае, следуя [4], случайную величину u будем обозначать
![]() .
.
Если ![]() , т. е.
, т. е. ![]() (i=1, 2,…,n), то распределение случайной величины u называют центральным
(i=1, 2,…,n), то распределение случайной величины u называют центральным ![]() -распределением или просто
-распределением или просто ![]() -распределением с n степенями свободы и случайную величину u будем обозначать
-распределением с n степенями свободы и случайную величину u будем обозначать
![]() .
.
Пусть ![]() . Величину
. Величину ![]() называют порогом или
называют порогом или ![]() - процентной точкой
- процентной точкой ![]() - распределения с n степенями свободы. Ее значения для различных
- распределения с n степенями свободы. Ее значения для различных ![]() и n[5,6]. Математическое ожидание и дисперсия случайной величины
и n[5,6]. Математическое ожидание и дисперсия случайной величины ![]() равны
равны
![]() .
.
Если ![]() и
и ![]() — независимые случайные величины, то из определения нецентрального
— независимые случайные величины, то из определения нецентрального ![]() -распределения сразу следует, что их сумма
-распределения сразу следует, что их сумма ![]() имеет нецентральное
имеет нецентральное ![]() - распределение с n=n1+n2 степенями свободы и параметров не центральности
- распределение с n=n1+n2 степенями свободы и параметров не центральности ![]() .
.
4. Результаты
Для доказательства независимости слагаемых ![]() и
и ![]() приведем следующие вспомогательные утверждения.
приведем следующие вспомогательные утверждения.
Лемма 4.1. Ранг суммы квадратичных форм не превосходит суммы их рангов.
Доказательство. Достаточно показать, что если ![]() и
и ![]() являются матрицами одного порядка и ранг
являются матрицами одного порядка и ранг ![]() равен
равен ![]() , то
, то ![]() . Для векторного пространства, порожденного столбцами
. Для векторного пространства, порожденного столбцами ![]() , выберем базис из
, выберем базис из ![]() векторов. Тогда так как столбцы
векторов. Тогда так как столбцы ![]() равны суммам соответствующих столбцов
равны суммам соответствующих столбцов ![]() и
и ![]() , то они являются линейными комбинациями
, то они являются линейными комбинациями ![]() векторов двух базисов; следовательно, число линейно независимых столбцов в
векторов двух базисов; следовательно, число линейно независимых столбцов в ![]() не может превосходить
не может превосходить ![]() . Следовательно,
. Следовательно, ![]() . Лемма доказана.
. Лемма доказана.
Следствие. Если ![]() , где ранг
, где ранг ![]() меньше или равен
меньше или равен ![]() ,
, ![]() , и если
, и если ![]() , то
, то ![]() ,
, ![]() .
.
Доказательство. Оно следует непосредственно из леммы 4.1. С одной стороны
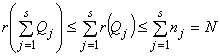 ,
,
а с другой стороны
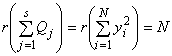
Следовательно,

При условии ![]() ,
, ![]() , выполнение последнего равенства возможно только тогда, когда
, выполнение последнего равенства возможно только тогда, когда ![]() ,
, ![]() , что и доказывает следствие.
, что и доказывает следствие.
Лемма 4.2. Если ![]() является квадратичной формой от переменных
является квадратичной формой от переменных ![]() и может быть выражена как квадратичная форма от переменных
и может быть выражена как квадратичная форма от переменных ![]() , являющихся линейными комбинациями
, являющихся линейными комбинациями ![]() , то
, то ![]() .
.
Доказательство. Пусть ![]() и
и ![]() , где
, где ![]() и
и ![]() симметричны. Тогда из равенства
симметричны. Тогда из равенства ![]() следует, что
следует, что ![]() , а по лемме 1.1 получаем:
, а по лемме 1.1 получаем: ![]() . Так как
. Так как ![]() – матрица размера
– матрица размера ![]() , то
, то ![]() . Лемма доказана.
. Лемма доказана.
Используя приведенные выше утверждения, приступим к доказательству независимости ![]() и
и ![]() . Так как
. Так как ![]() , то
, то
![]() , (4.1)
, (4.1)
где ![]() ;
; ![]() .
.
Определим ранги квадратичных форм ![]() ,
, ![]() и
и ![]() . Так как
. Так как ![]() , то
, то ![]() [1,2,6]. Перейдем к анализу квадратичной формы
[1,2,6]. Перейдем к анализу квадратичной формы
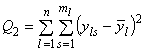 .
.
Введем переменные ![]() ,
, ![]() ;
; ![]() . Очевидно, что
. Очевидно, что
 .
.
Так как  , то
, то 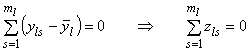 , поэтому
, поэтому
 .
.
Таким образом,
 .
.
Как видно из этого выражения, ![]() является квадратичной формой от
является квадратичной формой от ![]() переменных
переменных ![]() ,
, ![]() ;
; ![]() , где
, где ![]() . Поскольку переменные
. Поскольку переменные ![]() являются линейными комбинациями
являются линейными комбинациями ![]() , то, применяя лемму 4.2, получаем
, то, применяя лемму 4.2, получаем
![]() .
.
Следуя аналогичной схеме рассуждений для ![]() , применяя лемму 4, находим
, применяя лемму 4, находим
![]() .
.
Действительно, квадратичная форма ![]() от переменных
от переменных ![]() после некоторых преобразований может быть записана в виде
после некоторых преобразований может быть записана в виде ![]() , где
, где ![]() –
– ![]() -мерный вектор, а
-мерный вектор, а ![]() .
.
Но и без этого на основании следствия леммы 4.1, так как ![]() , получаем
, получаем ![]() ;
; ![]() ;
; ![]() .
.
В силу того, что случайные величины ![]() ,
, ![]() ,
, ![]() , независимы и имеют нормальное распределение
, независимы и имеют нормальное распределение ![]() , где
, где ![]() , то переход от равенства (4.1) к равенству
, то переход от равенства (4.1) к равенству
![]()
позволяет применить теорему Кохрана. По этой теореме случайные величины ![]() ,
, ![]() и
и ![]() независимы и имеют нецентральные
независимы и имеют нецентральные ![]() -распределения соответственно с
-распределения соответственно с ![]() ,
, ![]() и
и ![]() степенями свободы. Таким образом, независимость
степенями свободы. Таким образом, независимость ![]() и
и ![]() доказана.
доказана.
Замечание. Применяя теорему Кохрана для вычисления параметра нецентральности ![]() квадратичной формы
квадратичной формы ![]() , легко убедиться, что независимо от того, истинна гипотеза
, легко убедиться, что независимо от того, истинна гипотеза ![]() или нет,
или нет, ![]() , т.е. величина
, т.е. величина ![]() имеет центральное
имеет центральное ![]() -распределение:
-распределение:
 .
.
Список литературы
1.Асатурян В.И. Теория планирования эксперимента. М.: Радио и связь, 1883. 248 с.
2.Сидняев Н.И. Теория вероятностей и математическая статистика. М.: Юрайт, 2011. –170-190 с.
3. Тескин О.И. Статистическая обработка и планирование эксперимента . М.: МВТУ, 1982. 75 с.
4. Математическое моделирование интенсивности теплопередачи методами теории планирования эксперимента/ Сидняев Н.И. и др.//Инженерно-физичекий журнал. -2002. -Т.75, ╧2 -С.132-138.
5.Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных. М.: Юрайт, 2011. –95-220 с.
Публикации с ключевыми словами: дисперсионный анализ, нецентральное хи-квадрат распределение, адекватные модели, квадратичные суммы
Публикации со словами: дисперсионный анализ, нецентральное хи-квадрат распределение, адекватные модели, квадратичные суммы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



