научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2011
УДК 681.7.08
МГТУ им. Н.Э. Баумана
Одной из основных проблем создания крупных телескопов является обеспечение высокого качества изображения, что в свою очередь требует разработки высококачественных методов измерения и контроля формы асферических зеркал. Наиболее сложной является проблема контроля выпуклых поверхностей [1]. Попытка ее решения стандартными методами приводит к необходимости использования вспомогательных оптических элементов, диаметры которых существенно превышают диаметр самой контролируемой поверхности (КП).
Одним из примеров этого является контроль выпуклых гиперболических поверхностей с помощью сферы Хиндла [2] (рис.1). В этом случае диаметр эталонной поверхности (Э) существенно превышает диаметр КП.
|
Рис. 1. Схема контроля выпуклых гиперболических поверхностей с использованием сферы Хиндла |
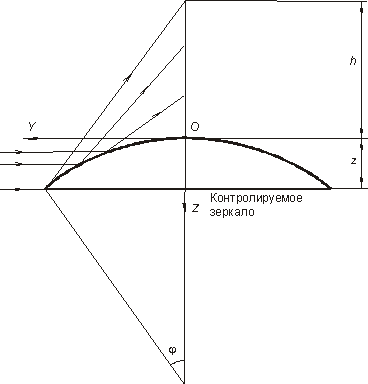
Попытка решения этой проблемы привела к созданию так называемой схемы ортогональных лучей[3, 4], согласно которой освещение контролируемой детали производится пучком параллельных лучей, ориентированных перпендикулярно оси симметрии детали (рис. 2).
|
Рис. 2. Схема ортогональных лучей |
Структура отраженного пучка несет в себе информацию о форме КП. Сущность контроля заключается в применении линзового растра (рис.3) для определения структуры светового пучка, отраженного от КП [5]. Каждый элемент растра представляет собой плоско-выпуклую линзу, центр кривизны сферической поверхности которой совпадает с плоской поверхностью.
|
|
а | б |
Рис. 3. К пояснению метода измерения и контроля формы выпуклых зеркал с использованием линзового растра: а – оптическая система; б – вид регистрируемого изображения | |
В процессе измерения при перемещении растра вдоль оси OZ определяются высоты hi опорного пучка и расстояния yi между центрами световых пятен, образованных опорным и отраженным световыми пучками (рис.3). Зная конструктивные параметры линзового растра и расстояния уi, можно определить углы ωi между лучами опорного и отраженного пучков, а значит и углы наклона нормалей φi (т.к. ωi = 2φi).
![]() (1)
(1)
где n – показатель преломления линзы; s – расстояние от плоской поверхности линзового растра до приемника излучения.
Путем аппроксимации определяется функция h(φ).
Профиль КП представляет собой сумму двух кривых: профиля АП второго порядка ближайшей к КП и величин местных погрешностей, т.е. отступлений КП от ближайшей АП (рис. 2). Параметрическое уравнение профиля КП имеет вид:
 (2)
(2)
Таким образом, для получения уравнения профиля КП необходимо решить две задачи:
1) определить геометрические параметры АП второго порядка, ближайшей к КП;
2) найти величины местных погрешностей.
Пусть RКП и kКП – реальные геометрические параметры КП, а RАП и kАП –геометрические параметры произвольной АП второго порядка.
|
Рис. 4. Реальный и теоретический профили контролируемой поверхности |
Теоретическая функция hАП(φ) для АП второго порядка, имеет вид:
![]() (3)
(3)
Зная эту зависимость и измеренную функцию hКП(φ) для КП, методом наименьших квадратов определяются геометрические параметры КП такие, чтобы теоретическая АП второго порядка была как можно ближе к КП:
 (4)
(4)
Наличие местных погрешностей формы КП вносит вклад в результат определение геометрических параметров. На рис. 5 а. показана КП с местной погрешностью в виде «бугра», а на рис. 5 б. – в виде «ямы».
При определении геометрических параметров ближайшей АП по формуле (4), получим геометрические параметры АП, отличающиеся от геометрических параметров КП. Для уменьшения влияния местных погрешностей вводится пороговое значение Δhпор величины отклонения местных погрешностей. При Δh> Δhпор принимается Δh = Δhпор.
|
|
а
| б |
Рис. 5. Виды погрешностей формы КП: а – «бугор»; б – «яма» | |
Для определения местных погрешностей формы КП получено параметрическое уравнение:
 (5)
(5)
в котором величина ∆h(φ) равна разности между измеренными высотами и высотами опорных пучков для АП с реальными значениями геометрических параметров, но без местных погрешностей.
Таким образом с помощью уравнений (4) и (5) можно получить профиль исследуемой поверхности.
Литература
1. Максутов Д.Д. Изготовление и исследование астрономической оптики (Изд. 2-е). М.: Наука. Главная редакция физико-математической литературы, 1984. 272 с.
2. Пуряев Д.Т. Методы контроля оптических асферических поверхностей. М.: Машиностроение, 1976. 262 с.
3. Goncharov A.V., Druzhin V.V., Batshev V.I. Non-contact methods for optical testing of convex aspheric mirrors for future large telescopes // Proc. SPIE. 2009. Vol. 7389. 7 p.
4. Способ измерения профиля оптических поверхностей: а.с. 1044969 СССР, МКИ4G01ВII/24./Д.Т. Пуряев (СССР). ╧3467407. 25 – 28; Заявлено 09.07.82; Опубликовано 30.09.83, Бюлл. ╧36. 3с.
5. Дружин В.В., Батшев В.И., Пуряев Д.Т. Измерение и контроль профиля светосильных выпуклых асферических зеркал на базе лазерного устройства с линзовым растром // Лазеры в науке, технике, медицине: Сб. научных трудов. – Москва, 2009. – Т. 20. – с. 109 – 111.
Публикации с ключевыми словами: контроль, асферическое зеркало, геометрические параметры, местные погрешности
Публикации со словами: контроль, асферическое зеркало, геометрические параметры, местные погрешности
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||