научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2011
УДК 519.816
МГТУ им. Н.Э. Баумана, г. Москва
РУДН, г. Москва
Задача оптимизации решений в дуэльной ситуации малых групп летательных аппаратов (ЛА) представляет собой совместную двухэтапную процедуру поиска оптимального целераспределения в конфликтной ситуации взаимодействия групп ЛА. Математические основы предлагаемого подхода подробно рассмотрены в статье [1].
Исходными данными для работы алгоритма являются базовые конфигурационные параметры каждого ЛА, участвующего во взаимодействии.
Алгоритм ранжирования первого этапа состоит из двух последовательных процедур:
1) сравнение по степени конфликтности (дуэльности) полного множества пар противодействующих ЛА;
2) выявление степени взаимной опасности ЛА в каждой паре.
Для каждого критерия определяются коэффициенты значимости, определяющие вклад того или иного критерия в значение многофакторной опасности объектов. Алгоритм ранжирования формируется на основе метода анализа иерархий (МАИ) Саати [2], который содержит три уровня: уровень целей, уровень критериев и уровень альтернатив-решений.
На втором этапе в результате оптимизации, процедура которой базируется на принципе конфликтной оптимальности на основе равновесия по Нэшу [3], формируется оптимальная матрица целераспределения (ЦР), в которой дается рекомендация к действию в той или иной складывающейся конфликтной ситуации взаимодействия ЛА. При этом производится учет множества конфигурационных характеристик ЛА с рассмотрением набора возможных решений. Данная рекомендация является необходимой для ситуации принятия решений в случае явной неоднозначности и неочевидности оптимальных действий каждого ЛА.
В работе [1] выбраны факторы взаимной опасности противодействующих ЛА, являющиеся источниками альтернатив для принятия решений в дуэльной ситуации.
Для определения коэффициентов опасности противодействия ЛА ![]() задача ЦР ЛА строится на основе метода анализа иерархий Саати. При этом задача оптимизации решений в дуэльной ситуации звеньев ЛА принимает вид совместной двухэтапной процедуры.
задача ЦР ЛА строится на основе метода анализа иерархий Саати. При этом задача оптимизации решений в дуэльной ситуации звеньев ЛА принимает вид совместной двухэтапной процедуры.
Алгоритм ранжирования первого этапа состоит из сравнения по степени конфликтности полного множества пар противодействующих ЛА ![]() и выявления степени взаимной опасности ЛА в каждой паре
и выявления степени взаимной опасности ЛА в каждой паре ![]() .
.
Для каждого фактора опасности ![]() определяются коэффициенты значимости
определяются коэффициенты значимости ![]() , определяющие вклад того или иного фактора в значение многофакторной опасности объектов
, определяющие вклад того или иного фактора в значение многофакторной опасности объектов ![]() , по которым определяется значение опасности
, по которым определяется значение опасности
![]() ,
,
где ![]() — нормированные значения;
— нормированные значения;
![]() — коэффициенты опасности противодействия
— коэффициенты опасности противодействия ![]() -го ЛА с ЛА
-го ЛА с ЛА ![]() , определяемые по текущим конфигурациям противодействующих групп ЛА.
, определяемые по текущим конфигурациям противодействующих групп ЛА.
Формируются матрицы ![]() обобщенных эффективностей противодействия ЛА
обобщенных эффективностей противодействия ЛА ![]() летательному аппарату
летательному аппарату ![]()
![]()
где ![]() — начальная вероятность поражения.
— начальная вероятность поражения.
Формируется блочная матрица эффективности противодействия ![]()
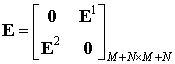 .
.
Например, для задачи противодействия ![]() ЛА (первую сторону противодействия представляют ЛА 1, ЛА 2, ЛА 3 и ЛА 4, остальные ЛА входят во вторую сторону) матрица эффективности противодействия
ЛА (первую сторону противодействия представляют ЛА 1, ЛА 2, ЛА 3 и ЛА 4, остальные ЛА входят во вторую сторону) матрица эффективности противодействия ![]() , используемая в дальнейшем, представлена в виде таблицы 1.
, используемая в дальнейшем, представлена в виде таблицы 1.
Таблица 1
Пример эффективностей противодействия ЛА
| ЛА 1 | ЛА 2 | ЛА 3 | ЛА 4 | ЛА 5 | ЛА 6 | ЛА 7 | ЛА 8 |
ЛА 1 | 0 | 0 | 0 | 0 | 0,3903 | 0,4299 | 0,3214 | 0,3128 |
ЛА 2 | 0 | 0 | 0 | 0 | 0,3924 | 0,3869 | 0,3990 | 0,3956 |
ЛА 3 | 0 | 0 | 0 | 0 | 0,5192 | 0,4299 | 0,4143 | 0,3335 |
ЛА 4 | 0 | 0 | 0 | 0 | 0,6087 | 0,5551 | 0,4112 | 0,3992 |
ЛА 5 | 0,5955 | 0,2695 | 0,3949 | 0,3305 | 0 | 0 | 0 | 0 |
ЛА 6 | 0,6507 | 0,2702 | 0,4155 | 0,3141 | 0 | 0 | 0 | 0 |
ЛА 7 | 0,5078 | 0,2713 | 0,2489 | 0,2285 | 0 | 0 | 0 | 0 |
ЛА 8 | 0,5408 | 0,2654 | 0,3290 | 0,2402 | 0 | 0 | 0 | 0 |
На втором этапе в результате оптимизации на основе равновесия по Нэшу формируется оптимальная матрица назначения ЛА звена на атаку, в которой дается рекомендация командиру звена к действию в конфликтной ситуации. При этом производится учет множества конфигурационных характеристик ЛА с рассмотрением набора возможных решений.
Критерий задачи конфликтно-оптимального ЦР – уравновешивание показателей взвешенных перевесов уничтоженных численностей противодействующих сторон по Нэшу
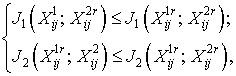
где ![]() — равновесное конфликтно-оптимальное ЦР обеих сторон;
— равновесное конфликтно-оптимальное ЦР обеих сторон;
![]() — оптимизируемые управляющие параметры, составляют матрицы ЦР по ЛА противника
— оптимизируемые управляющие параметры, составляют матрицы ЦР по ЛА противника ![]() При этом если значение
При этом если значение ![]() то ЛА с индексом
то ЛА с индексом ![]() не атакует ЛА с индексом
не атакует ЛА с индексом ![]() , а если
, а если ![]() то
то ![]() -му ЛА назначается на атаку ЛА с индексом
-му ЛА назначается на атаку ЛА с индексом ![]() .
.
Показатели взвешенного перевеса уничтоженных численностей имеют вид
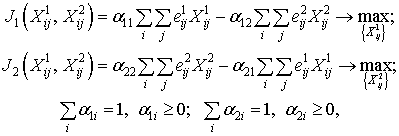
где ![]() — весовые коэффициенты, имеют смысл тактических свойств каждой системы при воздействии на противника.
— весовые коэффициенты, имеют смысл тактических свойств каждой системы при воздействии на противника.
В общем случае задача ЦР имеет смысл конфликтной задачи назначения (или размещения) со связями
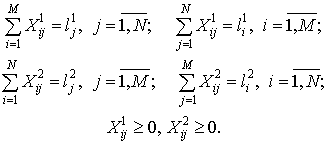
Для задачи назначения ![]() для задачи размещения
для задачи размещения ![]() где
где ![]() — целое число (но не больше числа ЛА в звене).
— целое число (но не больше числа ЛА в звене).
Уравновешивание перевесов уничтоженных численностей составляет один из вариантов естественного конфликтно-оптимального результата, одинаково учитывающего возможности обеих сторон в конфликте. Математически межсистемная устойчивость обеспечивается уравновешиванием показателей по Нэшу:
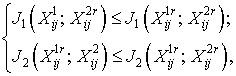
где ![]() — равновесное ЦР обеих сторон.
— равновесное ЦР обеих сторон.
Если задача имеет неединственное решение, то в качестве основного выбирается то решение, которое для обеих сторон является наиболее эффективным (наиболее близким к Парето-границе). Такое решение называется стабильно-эффективным компромиссом в дуэльной ситуации [3].
Для конфликтной ситуации двух участников эффективным алгоритмом решения задачи является процедура нахождения сетевого решения по Нэшу [3], которая обеспечивает более рациональный перебор допустимых вариантов решения, тем более при бинарном управлении в задаче ЦР. Это связано с тем, что в данной задаче заранее известен возможный набор решений, и поиск оптимального решения задачи ЦР ведется только по данному ограниченному множеству решений.
Начальным шагом данного алгоритма является формирование векторов управляющих параметров:
![]()
где ![]() — число допустимых решений каждой из сторон конфликта, которое вычисляется с учетом приведенных выше неравенств для
— число допустимых решений каждой из сторон конфликта, которое вычисляется с учетом приведенных выше неравенств для ![]() значения
значения ![]() представляют собой конкретное решение в форме матрицы ЦР (
представляют собой конкретное решение в форме матрицы ЦР (![]() ) для каждой стороны размерностями
) для каждой стороны размерностями ![]() и
и ![]() соответственно.
соответственно.
Таким образом, формируется равномерная ортогональная сетка по параметрам, на основании которой производится расчет значений показателей качества, представляющих собой точку на плоскости в координатах ![]()
![]()
В итоге формируется прямоугольная (при ![]() — квадратная, так как при этом
— квадратная, так как при этом ![]() ) трехмерная матрица показателей качества
) трехмерная матрица показателей качества ![]() размерностью
размерностью ![]() Обращение к показателю первой и второй сторон производится по третьему измерению матрицы. При построении формируется область значений показателей при всех возможных решениях
Обращение к показателю первой и второй сторон производится по третьему измерению матрицы. При построении формируется область значений показателей при всех возможных решениях ![]() .
.
Так, для представленной в виде таблицы 1 матрицы эффективностей противодействия ![]() , область показателей эффективности изображена на рисунке 1. При этом каждая точка представляет собой эффективность решения при заданных
, область показателей эффективности изображена на рисунке 1. При этом каждая точка представляет собой эффективность решения при заданных ![]() .
.
Далее реализуется алгоритм поиска сетевого решения по Нэшу.
Полученная задача второго этапа решается известными методами теории оптимизации управления многообъектными многокритериальными системами [3], которые являются комбинацией методов теории управления и антагонистических, бескоалиционных, коалиционных и кооперативных игр (с учетом уменьшающейся степени конфликтности).
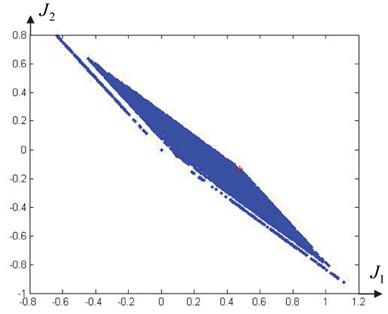
Рис. 1. Область значений показателей
На рисунке 1 конфликтно-оптимальное решение выделено красным цветом. Показатели взвешенного перевеса ![]() . Матрица конфликтно-оптимального ЦР, формирующая данное решение представлена в виде таблицы 2.
. Матрица конфликтно-оптимального ЦР, формирующая данное решение представлена в виде таблицы 2.
Таблица 2
Конфликтно-оптимальное ЦР
| ЛА 1 | ЛА 2 | ЛА 3 | ЛА 4 | ЛА 5 | ЛА 6 | ЛА 7 | ЛА 8 |
ЛА 1 |
|
|
|
| 0 | 1 | 0 | 0 |
ЛА 2 |
|
|
|
| 0 | 0 | 0 | 1 |
ЛА 3 |
|
|
|
| 0 | 0 | 1 | 0 |
ЛА 4 |
|
|
|
| 1 | 0 | 0 | 0 |
ЛА 5 | 0 | 0 | 0 | 1 |
|
|
|
|
ЛА 6 | 1 | 0 | 0 | 0 |
|
|
|
|
ЛА 7 | 0 | 1 | 0 | 0 |
|
|
|
|
ЛА 8 | 0 | 0 | 1 | 0 |
|
|
|
|
При вычислении конфликтно-оптимального ЦР, если число объектов сторон невелико, то достаточно использовать алгоритм полного перебора всевозможных вариантов ЦР, который передает данные в форме ортогональной сетки по управлениям ЦР (см. описание алгоритма) в процедуру оптимизации. Но если число объектов достаточно большое (4 и более), то алгоритм полного перебора не позволяет формировать данные в режиме реального времени, следовательно, необходимо сокращать число возможных вариантов ЦР для алгоритма оптимизации решения.
Так, время расчета конфликтно-оптимального целераспределения в программной среде пакета MATLAB для рассматриваемого примера превышает 24 секунды.
При этом становится актуальной задача повышения быстродействия алгоритма конфликтно-оптимального целераспределения. Одним из вариантов является предварительное решение задачи назначения по матрице эффективностей противодействия, которое будет служить базовым вариантом для построения на его основе множества допустимых решений.
Для приведения выполнения решения задачи в реальное время необходимо найти такие субоптимальные варианты решения задачи, которые, с одной стороны, являются достаточно эффективными и близкими к оптимальным, а с другой, обеспечивают нужное быстродействие. С этой целью можно производить предварительный анализ матрицы эффективности противодействия до ее передачи в процедуру оптимизации ЦР. По матрице эффективности противодействия для каждого ЛА выявляются заведомо малоэффективные по сумме всех показателей объекты из числа противников и при оптимизации ЦР они не учитываются. Таким образом, находится объект с минимальным среди всех коэффициентом по показателям начальной вероятности поражения и коэффициентам опасности объектов из звена противника и исключается. В каждом звене производится «просеивание» таких «слабых» объектов для каждого из звеньев и полученное множество допустимых решений передается в процедуру оптимизации ЦР, которая реализует принцип конфликтной оптимальности на основе Нэш-равновесия.
Для формирования матрицы Em для передачи во второй этап оптимизации сначала в каждой паре ![]() для каждого i-ого объекта находятся наименее эффективный j-ый объект по комбинированной опасности i-го объекта относительно j-го средства.
для каждого i-ого объекта находятся наименее эффективный j-ый объект по комбинированной опасности i-го объекта относительно j-го средства.
После процедуры предварительного «просеивания» наименее эффективных по комбинированной опасности объектов получается матрица Em со следующей структурой: она отличается от E тем, что в каждой строке присутствует по одному элементу, который не будет учитываться в процедуре нахождения оптимального целераспределения. В таблице 3 найденные наименее эффективные элементы выделены курсивом.
Таблица 3
Матрица эффективностей противодействия ЛА
ЛА 1 | ЛА 2 | ЛА 3 | ЛА 4 | ЛА 5 | ЛА 6 | ЛА 7 | ЛА 8 | |
ЛА 1 | 0 | 0 | 0 | 0 | 0,3903 | 0,4292 | 0,3214 | 0,3128 |
ЛА 2 | 0 | 0 | 0 | 0 | 0,3924 | 0,3869 | 0,3990 | 0,3956 |
ЛА 3 | 0 | 0 | 0 | 0 | 0,5192 | 0,4299 | 0,4143 | 0,3335 |
ЛА 4 | 0 | 0 | 0 | 0 | 0,6087 | 0,5551 | 0,4112 | 0,3992 |
ЛА 5 | 0,5955 | 0,2695 | 0,3949 | 0,3305 | 0 | 0 | 0 | 0 |
ЛА 6 | 0,6507 | 0,2702 | 0,4155 | 0,3141 | 0 | 0 | 0 | 0 |
ЛА 7 | 0,5078 | 0,2713 | 0,2489 | 0,2285 | 0 | 0 | 0 | 0 |
ЛА 8 | 0,5408 | 0,2654 | 0,3290 | 0,2402 | 0 | 0 | 0 | 0 |
В процедуре оптимизации ЦР учитываются все неотмеченные элементы матрицы Em и поскольку набор возможных решений заранее определен, производится менее ресурсоемкий поиск сетевого Нэш-решения и рассчитывается оптимальное ЦР.
На рис. 2 показана прореженная за счет отбрасывания заведомо проигрышных вариантов целераспределения область показателей эффективности.
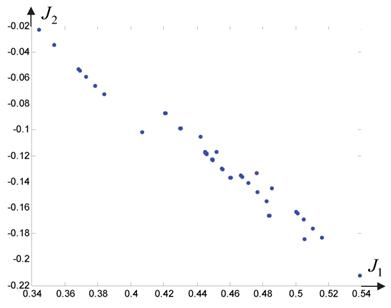
Рис. 2. Прореженная область значений показателей
Оптимальное ЦР, рассчитанное в соответствии с предлагаемой методикой полностью совпадает в данном примере с приведенным ранее в таблице 2 решением.
Показатели взвешенного перевеса ![]() .
.
Время выполнения расчета конфликтно-оптимального решения на современном персональном компьютере составляет 1,28 секунды.
При различных вариантах взаимодействия групп ЛА численностью 4x4 было установлено, что предварительный анализ матрицы с целью сокращения области поиска практически не сказывается на эффективности решения, т.е. не допускает потери оптимальных решений. Совпадение показателей взвешенного перевеса уничтоженных численностей и матриц оптимального целераспределения, полученных обеими способами, подтверждает уместность решения задачи с предварительным анализом матрицы эффективности противодействия до ее передачи в процедуру оптимизации ЦР. Поиск решения достигается с двадцатикратным ускорением, что является значительным результатом. При взаимодействии групп ЛА численностью 4x4 расчеты могут производиться в режиме, близком к реальному времени. Для задач большей размерности также достигается многократное ускорение вычислений.
При дальнейшем исследовании предполагается рассмотреть способы получения эффективных решений при взаимодействии групп ЛА численностью 5x5, а также возможности структурирования задачи при взаимодействии групп бόльших численностей.
Список использованных источников
1. Воронов Е.М., Карпунин А.А., Репкин А.Л. Двухэтапная задача оптимизации решений в дуэльной ситуации пар ЛА (звеньев ЛА) // Вестник РУДН. Инженерные исследования. — 2007. — ╧ 4. — C. 28–39.
2. Саати Т.Л. Принятие решений. Метод анализа иерархий: Пер. с англ. — М.: Радио и связь, 1993. — 314 с.
3. Воронов Е.М. Методы оптимизации управления многообъектными многокритериальными системами на основе стабильно-эффективных игровых решений: Учебник / Под ред. Н.Д. Егупова. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. — 576 с.
Публикации с ключевыми словами: назначение, летательный аппарат, целераспределение, ранжирование, равновесие по Нэшу, конфликтная оптимальность, групповое противодействие
Публикации со словами: назначение, летательный аппарат, целераспределение, ранжирование, равновесие по Нэшу, конфликтная оптимальность, групповое противодействие
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



