научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
УДК 621.396.967.029.7
МГТУ им. Н.Э. Баумана
Введение
Разработка систем автоюстировки (САЮ) приемо-передающих каналов высокоточных лазерных комплексов является актуальной задачей. Эти системы строятся на основе использования в функциональной схеме комплекса полунатурной модели его рабочего лазера – источника маркерного излучения [1, 2]. Как правило, в качестве маркерного источника используется маломощный лазер, работающий в видимом диапазоне спектра. Угловое положение оси пучка его излучения согласуется с высокой точностью с угловым положением оси пучка излучения рабочего лазера (РЛ). Далее, в приемо-передающих каналах комплекса пучок маркерного излучения является репером пространственного положения оси пучка излучения РЛ и используется для решения задач автоюстировки.
Пучки излучения маркера и РЛ должны последовательно проходить одни и те же оптические компоненты оптико-механического тракта, распространяясь в непосредственной близости друг от друга. Если сечение пучка излучения РЛ имеет форму кольца, то оптимальное положение пучка излучения маркера – в свободной зоне, на оси [3].
При проектировании САЮ необходимо исследовать особенности влияния на ее работоспособность дифракционных эффектов, связанных с распространением пучка излучения РЛ. Эти эффекты приводят к уширению распространяющегося пучка излучения РЛ. В результате элементы канала САЮ могут оказаться в зоне мощного излучения РЛ, что приводит к крайне нежелательным последствиям, связанным с появлением паразитных бликов в канале или с воздействием мощного излучения РЛ на оптические и механические элементы.
Проявление дифракционных эффектов необходимо проводить в пределах габаритов оптической системы САЮ. Обычно они соответствуют расстояниям до 20…30 метров по оптической оси от выходного зрачка РЛ.
1. Исследование параметров дифракционной картины для осевой точки при кольцевом сечении лазерного пучка
Рассмотрим дифракцию излучения РЛ на этих дальностях для кольцевой апертуры его выходного зрачка.
Пусть апертура РЛ представляет собой транспарант в виде кольцевой области с внутренним и внешним радиусами ![]() и
и ![]() соответственно (рис. 1). В первом приближении будем считать, что на вход апертурного транспаранта падает плоская монохроматическая волна с длиной волны λ. Свяжем с выходной апертурой РЛ координаты
соответственно (рис. 1). В первом приближении будем считать, что на вход апертурного транспаранта падает плоская монохроматическая волна с длиной волны λ. Свяжем с выходной апертурой РЛ координаты ![]() , а с плоскостью наблюдения, удаленной на расстояние
, а с плоскостью наблюдения, удаленной на расстояние ![]() , координаты
, координаты ![]() .
.

Рис. 1 – Геометрическая модель транспаранта апертуры рабочего лазера
В приближении скалярной теории дифракции [4] интеграл суперпозиции, описывающий преобразованный сигнал на выходе слоя пространства (СП), записывается в известном виде дифракционного интеграла Кирхгофа и имеет вид
![]() , (1)
, (1)
где ![]() – угол, образованный оптической осью и радиус вектором, проведенным из точки
– угол, образованный оптической осью и радиус вектором, проведенным из точки ![]() – источник волны, в точку
– источник волны, в точку ![]() ;
;
![]() расстояние от точки начала координат в плоскости транспаранта
расстояние от точки начала координат в плоскости транспаранта ![]() до точки
до точки ![]() регистрации дифракционной картины;
регистрации дифракционной картины;
![]() – значение комплексной амплитуды поля в точке М;
– значение комплексной амплитуды поля в точке М;
![]() – длина вектора, проведённого из точки
– длина вектора, проведённого из точки ![]() в точку
в точку ![]() .
.
Проанализируем выполнение условий приближения Френеля:
 . (2)
. (2)
При ![]() ,
, ![]() и
и ![]() приближения Френеля начинают действовать с расстояния соответственно l ≥ 4,66 м и l ≥ 5,526 м. Эти данные говорят о том, что для расчета дифракционных распределений в интересующей нас зоне (до 20…30 м по дальности) мы можем воспользоваться приближениями Френеля. Проведя известные преобразования [4], получаем выражение для распределения амплитуды поля в плоскости
приближения Френеля начинают действовать с расстояния соответственно l ≥ 4,66 м и l ≥ 5,526 м. Эти данные говорят о том, что для расчета дифракционных распределений в интересующей нас зоне (до 20…30 м по дальности) мы можем воспользоваться приближениями Френеля. Проведя известные преобразования [4], получаем выражение для распределения амплитуды поля в плоскости ![]() для осесимметричной функции, записанное в полярных координатах:
для осесимметричной функции, записанное в полярных координатах:
 , (3)
, (3)
где: ![]() ;
;
![]() - амплитуда падающей волны;
- амплитуда падающей волны;  – функция Бесселя первого рода нулевого порядка;
– функция Бесселя первого рода нулевого порядка; ![]() .
.
Результаты численного расчета по (3) дифракционной картины Френеля (в ближней зоне) при ![]() ,
, ![]() ,
, ![]() для различных расстояний
для различных расстояний ![]() от транспаранта приведены в таблице 1 и на рис. 2.
от транспаранта приведены в таблице 1 и на рис. 2.
Таблица 1
Параметры дифракционной картины
╧ п.п. | Расстояние | Радиус r внутренней окружности центральной зоны по уровню | Доля энергии |
1 | 4,66 | 28,85 | 0,005674 % |
2 | 10 | 27,6 | 0,011 % |
3 | 30 | 26,87 | 0,019 % |
4 | 50 | - | 0,026 % |

Рис. 2 – Нормированное распределение интенсивности в дифракционной картине Френеля на расстоянии 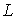 =10 м от транспаранта
=10 м от транспаранта
Особое внимание стоит обратить на центральный пик дифракционной картины. Этот пик периодически появляется и исчезает при увеличении расстояния ![]() , плотность мощности в его области может быть значительной. Отметим, что пучок излучения маркера распространяется именно по оси, поэтому возможно нежелательное воздействие излучения РЛ на элементы системы автоюстировки.
, плотность мощности в его области может быть значительной. Отметим, что пучок излучения маркера распространяется именно по оси, поэтому возможно нежелательное воздействие излучения РЛ на элементы системы автоюстировки.
Проанализируем закономерности формирования центрального пика. Выражение для амплитуды поля ![]() в точке
в точке ![]() при условии, что между источником сферической волны (т.
при условии, что между источником сферической волны (т. ![]() ) и т.
) и т. ![]() установлена круглая диафрагма (см. рис. 3) приводится в [4].
установлена круглая диафрагма (см. рис. 3) приводится в [4].

Рис. 3 – Построение зон Френеля при дифракции на отверстии
Это выражение имеет вид:
 (4)
(4)
Здесь ![]() - число зон Френеля,
- число зон Френеля, ![]() — коэффициент наклона, описывающий изменение амплитуды вторичных волн в зависимости от угла
— коэффициент наклона, описывающий изменение амплитуды вторичных волн в зависимости от угла ![]() между нормалью и направлением на точку наблюдения, а
между нормалью и направлением на точку наблюдения, а ![]() — угол между нормалью в точке
— угол между нормалью в точке ![]() и направлением
и направлением ![]() .
.
Если ![]() и
и ![]() велики по сравнению с длиной волны; то можно предположить, что в любой зоне Френеля величина
велики по сравнению с длиной волны; то можно предположить, что в любой зоне Френеля величина ![]() постоянна и в зоне
постоянна и в зоне ![]() равна
равна ![]() . Знак «+» берется при нечетном N, а «-» при четном N числе открытых зон Френеля.
. Знак «+» берется при нечетном N, а «-» при четном N числе открытых зон Френеля.
Рассмотрим теперь несколько частных случаев количества зон Френеля, полезных для дальнейших выводов:
1) Если между т. Р и т. Ро нет препятствия т.е. открыты все зоны Френеля, то
![]() (5)
(5)
Для последней зоны ![]() , видимой из т.
, видимой из т.![]() ,
, ![]() становится касательной к волновому фронту, т.е.
становится касательной к волновому фронту, т.е. ![]() , и величина
, и величина ![]() . Следовательно:
. Следовательно:
 (6)
(6)
Приведенное выражение показывает, что полное возмущение в т. при отсутствии препятствия между т. ![]() и т.
и т.![]() равняется половине возмущения, обусловленного действием первой зоны Френеля. Действие первой зоны Френеля с точностью до знака определяется функцией наклона
равняется половине возмущения, обусловленного действием первой зоны Френеля. Действие первой зоны Френеля с точностью до знака определяется функцией наклона ![]() , тогда:
, тогда:
 . (7)
. (7)
Если открыта только одна первая зона, то возмущение в т. ![]() на основании (4)
на основании (4)
 , (8)
, (8)
и интенсивность ![]()
![]() в четыре раза больше, чем в отсутствие экрана.
в четыре раза больше, чем в отсутствие экрана.
При дальнейшем увеличении отверстия интенсивность уменьшится, так как ![]() и
и ![]() в (4) имеют разные знаки. Больше того, значения
в (4) имеют разные знаки. Больше того, значения ![]() и
и ![]() почти одинаковы, и, следовательно, если отверстие приблизительно равно двум первым зонам, то в точке
почти одинаковы, и, следовательно, если отверстие приблизительно равно двум первым зонам, то в точке ![]() будет почти полная темнота. Поэтому при изменении размеров отверстия наблюдается периодическое изменение интенсивности в
будет почти полная темнота. Поэтому при изменении размеров отверстия наблюдается периодическое изменение интенсивности в ![]() . Такой же результат получается и тогда, когда размеры отверстия и источника остаются постоянными, а точка наблюдения
. Такой же результат получается и тогда, когда размеры отверстия и источника остаются постоянными, а точка наблюдения ![]() перемещается вдоль оси. В этом случае при постепенном приближении точки
перемещается вдоль оси. В этом случае при постепенном приближении точки ![]() к экрану увеличивается число открывающихся зон.
к экрану увеличивается число открывающихся зон.
Для существенного упрощения аналитических расчетов будем считать, что волновой фронт излучения рабочего лазера, падающий на кольцевую диафрагму, близок к плоскому. Обобщим выражение (4) на случай, если на диафрагму падает плоская волна.
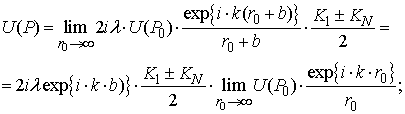 (9)
(9)
Выражение  представляет собой амплитуду сферической волны на расстоянии
представляет собой амплитуду сферической волны на расстоянии ![]() от источника. В пределе при
от источника. В пределе при ![]() , стремящемся к бесконечности, волновой фронт в пределах диафрагмы можно считать плоским, а распределение амплитуды в плоскости установки диафрагмы постоянным и равным амплитуде падающей волны
, стремящемся к бесконечности, волновой фронт в пределах диафрагмы можно считать плоским, а распределение амплитуды в плоскости установки диафрагмы постоянным и равным амплитуде падающей волны ![]() .
.
Рассмотрим теперь случай установки кольцевой диафрагмы, приведённой на рисунке 1, которая соответствует выходной апертуре резонатора РЛ.
На основании приведенных выше выкладок (4) можно сделать вывод, что максимум интенсивности для осевой точки будет наблюдаться на расстоянии, при котором на кольцевой диафрагме будет укладываться нечётное число зон Френеля.
Как видно из рис. 2, в центральной экранированной зоне (для осевых точек) имеется ярко выраженный пик интенсивности излучения. Интенсивность осевого пика в максимуме в четыре раза превышает интенсивность излучения в плоскости транспаранта. Причем характер изменения интенсивности для осевой точке при изменении расстоянии от транспаранта до точки наблюдения дифракционной картины имеет сложную зависимость. Как показывает теория дифракции Френеля [4] это будут чередующие минимумы и максимумы с изменяющимся периодом в зависимости от того четное или нечетное число зон Френеля открывается на транспаранте для данного удаления ![]() от него.
от него.
Выражение (9) сложно для анализа положений максимумов дифракционной картины. Получим выражение для зависимости интенсивности осевой точки от числа открытых зон Френеля (фактически, от расстояния между транспарантом и точкой наблюдения ![]() ).
).
Общее число зон Френеля, укладывающихся на кольцевой диафрагме на расстоянии ![]() (см. рис. 3) можно рассчитать по следующему выражению:
(см. рис. 3) можно рассчитать по следующему выражению:
![]() (10)
(10)
где ![]() модуль радиус вектора, проведённого из точки на внешнем радиусе кольцевой диафрагмы при
модуль радиус вектора, проведённого из точки на внешнем радиусе кольцевой диафрагмы при ![]() (см. рисунок 3) в точку
(см. рисунок 3) в точку ![]() .
.
![]() (11)
(11)
где ![]() модуль радиус вектора, проведённого из точки на внутреннем радиусе кольцевой диафрагмы
модуль радиус вектора, проведённого из точки на внутреннем радиусе кольцевой диафрагмы ![]() в точку.
в точку.
![]() (12)
(12)
Тогда выражение для общего числа зон Френеля, укладывающихся на кольцевой диафрагме в зависимости от расстояния ![]() до точки наблюдения
до точки наблюдения ![]() имеет вид:
имеет вид:
![]() (13)
(13)
График функции числа зон Френеля ![]() (положений минимумов и максимумов для осевых точек) представлен на рис. 4.
(положений минимумов и максимумов для осевых точек) представлен на рис. 4.

Рис. 4 – Число зон Френеля, укладывающихся на кольцевой диафрагме, в зависимости от расстояния до осевой точки наблюдения
Как видно из рис. 4, число зон Френеля, укладывающихся на кольцевой апертуре, уменьшается с увеличением расстояния до точки ![]() .
.
На рис. 5 показана графическая зависимость интенсивности ![]() , рассчитанная численным методом по (3), для осевых точек наблюдения в зависимости от расстояния до транспаранта
, рассчитанная численным методом по (3), для осевых точек наблюдения в зависимости от расстояния до транспаранта ![]() на интервале
на интервале ![]() от 3000 мм до 3018 мм и для приведенных выше исходных данных.
от 3000 мм до 3018 мм и для приведенных выше исходных данных.
Функцию интенсивности для осевых точек в зависимости от расстояния b можно аппроксимировать следующим образом:
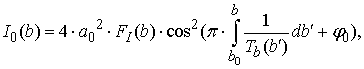 (14)
(14)
где ![]() - функция, промодулированная по амплитуде и по частоте,
- функция, промодулированная по амплитуде и по частоте,
FI(b) – функция изменения пикового значения интенсивности осевых точек в зависимости от расстояния b,
Tb(b) – зависимость изменения периода осциллирующей функции.
Рис. 5 – Зависимость интенсивности ![]() для осевых точек наблюдения на интервале расстояний
для осевых точек наблюдения на интервале расстояний
Так как функция ![]() является квазилинейной на участке значений функции
является квазилинейной на участке значений функции ![]() , разложив её в ряд Тейлора в окрестности
, разложив её в ряд Тейлора в окрестности ![]() , и ограничившись двумя первыми членами разложения, получим:
, и ограничившись двумя первыми членами разложения, получим:
![]()
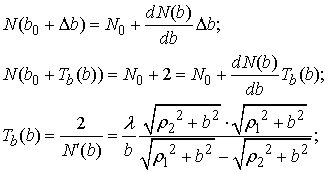 (15)
(15)
где ![]() число зон Френеля, укладывающихся на апертуре на расстоянии
число зон Френеля, укладывающихся на апертуре на расстоянии ![]() от неё.
от неё.
График изменения периода ![]() осциллирующей функции интенсивности
осциллирующей функции интенсивности ![]() представлен на рис. 6.
представлен на рис. 6.
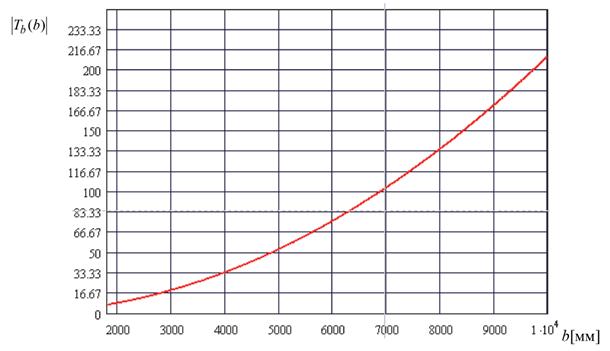
Рис. 6 – Функция изменения периода осциллирующей функции интенсивности на оси от расстояния между транспарантом и точкой наблюдения ![]()
2. Исследование возможности подавления центрального пика дифракционной картины
Метод снижения интенсивности центрального пика дифракционной картины для кольцевой апертуры РЛ очевидным образом вытекает из приведенных соотношений. Он заключается в том, что добиться снижения или полного подавления интенсивности в конкретной точке на оси можно с помощью установки дополнительной диафрагмы между выходным окном РЛ и рассматриваемой точкой ![]() . В результате выставки диафрагмы из т.
. В результате выставки диафрагмы из т. ![]() должно наблюдаться либо четное число зон Френеля на выходном окне РЛ, либо выходное окно должно полностью виньетироваться.
должно наблюдаться либо четное число зон Френеля на выходном окне РЛ, либо выходное окно должно полностью виньетироваться.
На рис. 7 показано расположение выходного окна РЛ, пучок излучения маркера, вводимый по оси с помощью пентапризмы, возможное расположение диафрагм и рассматриваемая т. ![]() .
.

Рис. 7. Расположение диафрагм, устраняющих дифракционный максимумы для осевой точки наблюдения Р
Расстояние от точки P до диафрагмы в предельном случае ограничения радиуса виньетирующей диафрагмы сверху, т.е. ![]() найдём из следующего соотношения:
найдём из следующего соотношения:
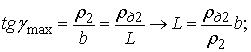 (16)
(16)
где ![]() внешний радиус диафрагмы.
внешний радиус диафрагмы.
Назначим ![]() из условия отсутствия виньетирования пучка излучения РЛ, т.е.
из условия отсутствия виньетирования пучка излучения РЛ, т.е. ![]() .
.
Также следует учесть, что в приосевой зоне распространяется излучение маркёра с диаметром пучка ![]() . Из технологических соображений внутренний радиус диафрагм назначим
. Из технологических соображений внутренний радиус диафрагм назначим ![]() .
.
Из-за сложности аналитического расчета дифракции на множестве последовательных виньетирующих диафрагм, моделирование проведем с помощью численных методов в САПР «Zemax».
Рассмотрим точку, удалённую от апертуры на расстояние ![]() при
при ![]() ,
, ![]() и длине волны излучения РЛ
и длине волны излучения РЛ ![]() . Из соотношения (9) для этой точки получим
. Из соотношения (9) для этой точки получим ![]() , вследствие этого для точки на оси наблюдается резкий пик интенсивности (см. рис. 8).
, вследствие этого для точки на оси наблюдается резкий пик интенсивности (см. рис. 8).
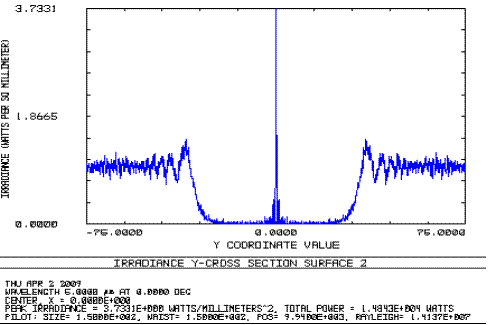
Рис. 8 – Распределение интенсивности в плоскости регистрации дифракционнной картины в отсутствие виньетируюшей диафрагмы
Установка диафрагмы на расстоянии ![]() в соответствии с рисунком 7 полностью исключает увеличение интенсивности для рассматриваемой осевой точки, что показано на рис. 9. Последовательно рассчитывая положения максимумов для расстояний, меньших
в соответствии с рисунком 7 полностью исключает увеличение интенсивности для рассматриваемой осевой точки, что показано на рис. 9. Последовательно рассчитывая положения максимумов для расстояний, меньших ![]() , определим положения серии диафрагм, обеспечивающих уменьшение центральных пиков интенсивности в диапазоне расстояний
, определим положения серии диафрагм, обеспечивающих уменьшение центральных пиков интенсивности в диапазоне расстояний ![]() от 0 до
от 0 до ![]() (см. Таблицу 2)
(см. Таблицу 2)
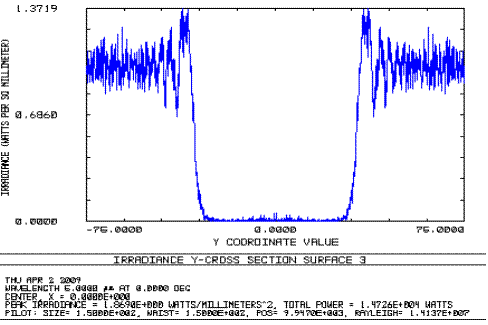
Рисунок 9 – Распределение интенсивности в плоскости регистрации дифракционнной картины при наличии виньетируюшей диафрагмы
Таблица 2
Расположение виньетирующих диафрагм
╧ диафрагмы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Расстояние между диафрагмами, мм | 1213,6 | 132,7 | 141,4 | 165,0 | 181.9 | 197,3 | 226,7 | 283,7 | 278,3 | 346,7 |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
398,5 | 399,0 | 499,5 | 300,0 | 165,9 | 271,2 | 303,0 | 109,2 | 350,4 |
Такое расположение диафрагм позволяет полностью исключить центральный пик интенсивности на расстояниях ![]() от 2 до 10 м, что подтверждается соответствующими расчетами, проведенными с помощью САПР «Zemax».
от 2 до 10 м, что подтверждается соответствующими расчетами, проведенными с помощью САПР «Zemax».
Выводы
В результате проведённых исследований показана принципиальная возможность снижения интенсивности центрального пика за счёт специально рассчитанных диафрагм, установленных вдоль оси распространения излучения рабочего лазера.
Список используемой литературы.
1. Н.В.Барышников, В.В.Карачунский, В.И.Козинцев А.С.Румянцев, Д.В.Худяков. Разработка и экспериментальные исследования оптико-электронной системы автоюстировки. Тезисы докладов III научно-технической конференции «Радиооптические технологии в приборостроении», 12-16 сентября 2005г., г.Сочи, Россия, с.172 – 177.
2. Н.В.Барышников, В.В.Карачунский, В.И.Козинцев А.С.Румянцев, Д.В.Худяков, Использование методов полунатурного моделирования для исследования характеристик системы автоюстировки Тезисы докладов IV НТК «Радиооптические технологии в приборостроении», Сочи, 2006 г., с. 105 – 108.
3. Барышников Н.В. Исследование пространственных характеристик пучка излучения лазера при его нелинейном взаимодействии со средой распространения: Вестник МГТУ им.Н.Э.Баумана. Приборостроение.- 2011. ╧2(83), с.3 - 15
4. Основы оптики. Борн М., Вольф Э. Перевод с английского. Главная редакция физико-математической литературы изд-ва «Наука», 1970, 856с.
Публикации с ключевыми словами: система автоюстировки, рабочий лазер, маркерный источник, дифракционная картина, зона Френеля, амплитуда поля, кольцевая диафрагма
Публикации со словами: система автоюстировки, рабочий лазер, маркерный источник, дифракционная картина, зона Френеля, амплитуда поля, кольцевая диафрагма
Смотри также:
- 77-30569/241632 Исследование влияния излучения рабочего лазера на работу систем автоюстировки высокоточных лазерных приборов
- Исследование влияния угловых аберраций объектива оптико-электронного координатора на погрешности измерения взаимного углового рассогласования осей лазерных пучков
- Алгоритм генерации псевдослучайных чисел для компьютерного симулятора двухщелевой дифракции одиночных микрочастиц
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



