научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
УДК.658:005.5
ФБГОУ ВПО МГТУ «СТАНКИН»
Система управления ремонтами является одним из важных элементов в системе управления предприятием. Исследования консалтинговых компаний показали высокую эффективность от внедрения систем управления ремонтами оборудования на промышленных предприятиях [1]. Система управления ремонтами оборудования решает задачи обеспечения непрерывности технологического процесса предприятия [2]. Одной из важных задач является задача календарного планирования ремонтов технологического оборудования предприятия.
В зависимости от периода планирования выделяют 3 вида календарного плана ремонта оборудования: годовой, месячный, недельный. Годовой план составляют в конце года на основании информации о техническом состоянии оборудования. Месячный план составляется в конце каждого месяца на основе годового плана и текущего состояния оборудования. Недельный план ремонтов составляется в конце недели (пятница). Он разрабатывается на основе месячного плана ремонтов, учитывает текущее состояние оборудования, а также изменение количества всех видов ресурсов, произошедшее в течение месяца.
Опишем основные параметры задачи календарного планирования ремонтов оборудования предприятия. Задана система, которая состоит из множества машин и набора работ (заявок, требований на обслуживание). Для системы задаются следующие параметры: моменты поступления, ранее которых обслуживание заявок не может быть начато; продолжительность выполнения заявок машиной; директивный срок, к которому необходимо или желательно завершить обслуживание заявки; весовой коэффициент, характеризующий относительную важность заявки; неубывающая функция, определяющая стоимость обслуживания заявки при условии, что обслуживание завершится в определенный момент времени. Целевая функция описывает критерий оптимизации. Она зависит от следующих параметров: момент завершения обслуживания, временное смещение (разница между моментом завершения обслуживания и директивным сроком окончания обслуживания), запаздывание (равно положительному значению временного смещения, либо нулю в противном случае).
Задачи составления календарных планов работ относятся к классу задач, изучаемых в рамках теории расписаний, появившейся в 50-е годы XX века [3]. Развитием данного направления науки занимались известные ученые: Беллман Р. [4], Гэри М., Джонсон C. [5], Брукс Г.Н., Брукер П., Конвей Р. [6], Максвелл В., Миллер Л., Танаев В.С.[3], Шкурба В.В. [3], Гордон В.С., Шафранский Я.Н., Прилуцкий М.Х. [7], Норенков И.П. [8], Лазарев А.А. и др.
Рассматриваемая задача является задачей календарного планирования с ограниченными ресурсами. В задаче календарного планирования с ограниченными ресурсами задано множество работ, связанных друг с другом условиями предшествования. Для каждой работы задана длительность ее выполнения и объем потребляемых ресурсов. Суммарный объем каждого ресурса считается известным в каждый момент времени. Требуется найти расписание выполнения работ, удовлетворяющее условиям предшествования, ограничениям по ресурсам и минимизирующее суммарное отклонение фактического начала выполнения работ от директивных сроков.
Сформулируем математическую постановку задачи календарного планирования технического обслуживания и ремонтов оборудования промышленного предприятия [9].
Введем обозначение периода планирования:
![]()
где t – момент времени на интервале планирования, T – длительность периода планирования.
Дано множество цехов на предприятии:
![]()
где CEс – с-ый цех на предприятии; С – количество цехов на предприятии.
Множество линий по производству продукции на предприятии:
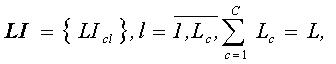
где LIcl – l-ая производственная линия в цехе c; Lc – количество линий в цехе c, L – количество линий на предприятии.
Множество марок оборудования:

где MO(c,l,m) – m-ая марка оборудования в линии номер l в цехе c; Mcl – количество марок оборудования в линии номер l в цехе c; M – количество марок оборудования.
Множество единиц оборудования на предприятии:
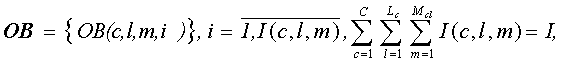
где OB(c,l,m,i) – i-ая единица оборудования марки m в линии номер l в цехе c, I(c,l,m) – количество единиц оборудования марки m в линии l в цехе c; Mcl – количество марок оборудования в линии l в цехе c; I – количество единиц оборудования на предприятии.
Введем описание ресурсов, необходимых для выполнения работ. Множество трудовых ресурсов имеющихся на предприятии:
![]()
где RTv – количество ресурса вида v; v – номер вида ресурса (вид ресурса – уровень квалификации рабочих, выполняющих работы); V – количество видов ресурсов.
Множество видов ремонтных работ (техническое обслуживание, текущий ремонт, капитальный ремонт) для каждой единицы оборудования:

где VS(c,l,m,i,n) – n-ый вид ремонтной работы для единицы оборудования i марки оборудования m, которая находится в линии l в цехе c; N(c,l,m,i) – количество видов ремонтных работ для единицы оборудования i марки оборудования m, которая находится в линии l в цехе c; N – общее количество видов ремонтов.
Множество плановых ремонтных работ для всех единиц оборудования определим как:

где SO(c,l,m,i,n,z) – z-ая ремонтная работа вида n для единицы оборудования i марки оборудования m, которая находится в линии l в цехе c; Z(c,l,m,i,n) – количество ремонтных работ вида n для i-ой единицы оборудования марки m, которая находится в линии l в цехе c; Z – общее количество плановых ремонтных работ на рассматриваемом периоде планирования.
Множество трудовых ресурсов необходимых для выполнения ремонтных работ различного вида для каждой единицы оборудования (нормативная информация):
![]()
где RTO(c,l,m,i,n,v) – количество трудового ресурса вида v необходимого для выполнения ремонтной работы вида n над i-ой единицей оборудования марки m, которая находится в линии l в цехе c.
Множество директивных (рекомендуемых по нормативам) моментов начала выполнения работ для всех единиц оборудования:
![]()
где TD(c,l,m,i,n,z) – директивный момент начала z-ой работы вида n единицы оборудования i марки оборудования m, которая находится в линии l в цехе c.
Множество межремонтных интервалов (периодичность ремонта) между видами работ, измеряется в часах (нормативная информация):
![]()
где MI(c,l,m,i,n,z) – межремонтный интервал z-ой работы вида n единицы оборудования i марки оборудования m, которая находится в линии l в цехе c.
Далее опишем варьируемые параметры рассматриваемой задачи.
Множество моментов начала выполнения работ:
![]()
где TN(c,l,m,i,n,z) – момент начала z-ой работы вида n единицы оборудования i марки оборудования m, которая находится в линии l в цехе c.
Множество моментов окончания выполнения работ:
![]()
где TK(c,l,m,i,n,z) – момент окончания z-ой работы вида n единицы оборудования i марки оборудования m, которая находится в линии l в цехе c.
Формула расчета момента окончания каждой работы:
![]()
где f1(RTO(c,l,m,i,n,v),SO(c,l,m,i,n,z)) – функция расчета затрат количества трудовых ресурсов на выполнение z-ой работы вида n единицы оборудования i марки оборудования m, которая находится в линии l в цехе c.
Формула расчета момента начала каждой работы:
![]()
Опишем множество групп одновременно выполняемых работ на всем периоде планирования:
![]()
где ![]() – w-ая группа (множество) одновременно выполняемых работ; W – общее количество групп одновременно выполняемых работ на всем периоде планирования.
– w-ая группа (множество) одновременно выполняемых работ; W – общее количество групп одновременно выполняемых работ на всем периоде планирования.
Опишем множество одновременно выполняемых работ группы w, которые находятся в состоянии выполнения в период времени [tw1,tw2]:
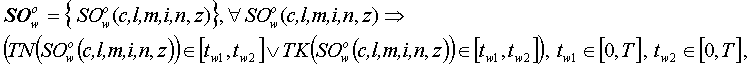
где SOwo(c,l,m,i,n,z) – z-ая работа вида n единицы оборудования i марки оборудования m, которая расположена в линии l в цехе c и находится в состоянии выполнения в группе w одновременно выполняемых работ; tw1 – начало периода w-ой группы одновременно выполняемых работ; tw2 – конец периода w-ой группы одновременно выполняемых работ.
Для решения задачи календарного планирования на предприятии могут быть использованы следующие критерии оптимизации.
Первым критерием оптимизации будет минимизация функции стоимости, т.е. суммы отклонений директивных и фактических моментов начала всех запланированных работ для всех единиц оборудования:

где F1(SO) – критерий оптимизации по функции стоимости; f2(SO(…),TD(…),TN(…)) – функция, которая определяет величину стоимости выполнения работы SO(…) в зависимости от разницы между директивным сроком начала выполнения работы TD(…) и фактическим началом выполнения работы TN(…), чем меньше отклонение, тем меньше значение функции стоимости; SO – множество всех плановых работ.
Вторым критерием оптимизации будет максимальное использование имеющихся трудовых ресурсов на всех работах по ремонту оборудования, которые находятся в состоянии выполнения. Смысл критерия заключается в сокращении времени простоя ремонтных бригад.
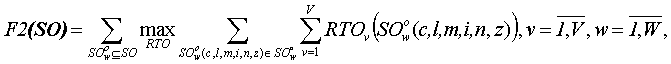
где F2(SO) – критерий оптимизации по трудовым ресурсам; RTOv(SOwo(c,l,m,i,n,z)) – количество трудового ресурса вида v, выделенного для выполнения ремонтной работы SOwo(c,l,m,i,n,z); SOwo – w-ая группа (множество) одновременно выполняемых работ.
Третьим критерием оптимизации будет минимизация общей длительности простоя линии предприятия при ремонте оборудования:

где F3(SO) – критерий оптимизации по длительности простоя линий предприятия; f3(SO(…),TN(…),TK(…)) – функция, которая определяет длительность простоя линии l в цехе c на всем периоде планирования, за счет суммирования времени выполнения ремонтных работ SO(…); Mcl – количество марок оборудования в линии номер l в цехе c; I(c,l,m) – количество единиц оборудования марки m в линии l в цехе c; N(c,l,m,i) – количество видов ремонтных работ для единицы оборудования i марки оборудования m, которая находится в линии l в цехе c; Z(c,l,m,i,n) – количество ремонтных работ вида n для i-ой единицы оборудования марки m, которая находится в линии l в цехе c.
Ограничение по трудовым ресурсам для всех групп одновременно выполняемых работ можно описать как:
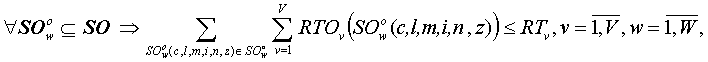
где SOwo(c,l,m,i,n,z) – z-ая работа вида n единицы оборудования i марки оборудования m, которая расположена в линии l в цехе c и находится в состоянии выполнения в группе w одновременно выполняемых работ;
Известны следующие методы решения задачи календарного планирования (рис. 1): математическое программирование, комбинаторные методы, статистические методы и эвристические методы.

Рис. 1. Методы календарного планирования
Анализ приведенных методов показал, что сложность использования как комбинаторного метода, так и метода динамического программирования связана с экспоненциальным ростом длительности вычислений от размерности задачи. К тому же в задачах календарного планирования на каждом шаге планирования изменяется система ограничений, что затрудняет применение симплекс-метода, как части метода ветвей и границ. Для использования имитационного моделирования необходим большой объем статистических данных, доступ к которым на предприятии обычно затруднен. Таким образом, наиболее перспективным будет выбор эвристических методов. В настоящий момент разработано множество эвристических методов, основанных на применении генетических алгоритмов и их модификаций [8, 10-12], позволяющих находить близкое к оптимальному решение задачи календарного планирования с ограниченными ресурсами. На основании проведенного анализа для решения задачи календарного планирования ремонтов оборудования предприятия был разработан алгоритм построения оптимального календарного плана на основе генетического алгоритма. Блок-схема работы генетического алгоритма применительно к рассмотренной задаче представлен на рис. 2.
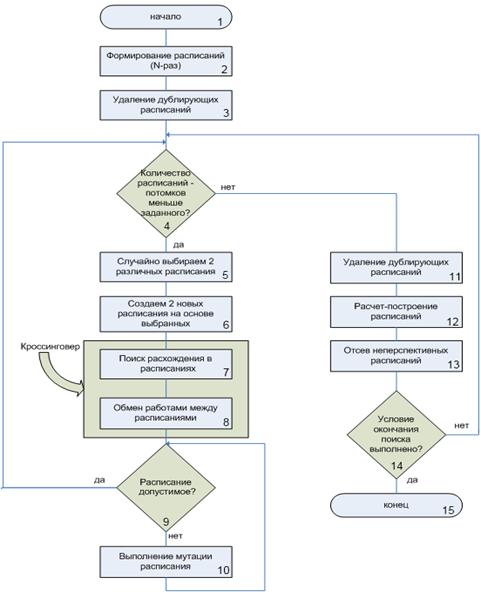
Рис. 2. Генетический алгоритм составления календарного плана
В начале выполнения алгоритма произвольным образом формируется множество расписаний (начальная популяция – блок 2). Далее созданное множество проверяется на наличие повторяющихся расписаний и выполняется удаление дублей (блок 3). Следующий этап – это случайный выбор с равной вероятностью двух исходных расписаний (блок 5) и на их основании создаются два новых расписания идентичных исходным (блок 6). В блоках 7, 8 выполняется поиск расхождения в созданных расписаниях и обмен работами между расписаниями – операция кроссинговер. Сначала выполняется попарное сравнение работ в расписаниях и при нахождении первого расхождения в последовательности выполняется обмен работами между расписаниями. Если в полученных расписаниях образуются дублирующие работы, то продолжаем выполнять обмен работами до исчезновения дублирования работ в каждом расписании. В блоке 9 проводится проверка допустимости расписания, т.е. для всех работ расписания проверяется выполнение условия предшествования работ. Если условие не выполняется, то производится «мутация» расписания (блок 10). Работы, которые не удовлетворяют условию предшествования, меняются местами до тех пор, пока расписание не станет допустимым. Пусть по условиям предшествования в расписании работа 1.1 (для первой единицы оборудования первая работа) должна предшествовать работе 1.2 (для первой единицы оборудования вторая работа). Тогда если после проверки допустимости расписания (блок 9) оказалось, что работа 1.2 находится перед работой 1.1, то соответственно выполняется перестановка этих работ между собой местами. После выполнения заданного количества операций кроссинговера выполняется удаление дублирующих расписаний (блок 11). В блоке 12 выполняется расчет расписаний. Определяется сумма отклонений сроков фактического начала работ от директивных. После этого производится сортировка расписаний и отсев неперспективных расписаний (блок 13). Число неперспективных расписаний определяется таким образом, чтобы полученная популяция (репродукционная группа) имела размер исходной популяции. Выполнение блоков 4-13 повторяется до тех пор, пока не будет выполнено условие окончания поиска решения задачи: значение критерия оптимизации лучшего решения не изменяется в десяти последующих популяциях. На основе описанного алгоритма был разработан программный комплекс по ведению базы данных оборудования, расчета и построения календарного графика ремонтов технологического оборудования предприятия. На рис. 3 представлен график сходимости целевой функции к оптимальному или близкому к оптимальному значению, полученный на основании данных реального промышленного предприятия.

Рис. 3. График схождения к оптимальному решению
В статье сформулирована математическая постановка задачи календарного планирования ремонтов технологического оборудования промышленного предприятия. Данная задача относится к классу задач календарного планирования с ограниченными ресурсами. На основании анализа методов решения данного класса задач был выбран эвристический метод, основанный на генетическом алгоритме. Разработан алгоритм и реализующий его программный комплекс для решения поставленной задачи календарного планирования ремонтов технологического оборудования предприятия.
Литература:
1. Мышенков К.С., Романов А.Ю. Система управления ремонтами оборудования, как элемент системы стратегического управления предприятием // Стратегическое управление организациями: проблемы и возможности современной экономики: Сб. науч. тр. – СПб.: Изд-во Политехн. ун-та, 2009. – Ч. 1. – С. 77-83.
2. Романов А.Ю. Структурный анализ системы управления ремонтами оборудования кондитерской фабрики // Общеуниверситетская науч. конф. молодых ученых и спец.: Сб. матер. / Отв. ред. С.А. Хуршудян. – М.: Изд. комплекс МГУПП, 2009. – С. 305-311.
3. Танаев В.С., Шкурба В.В. Введение в теорию расписаний. – М: Изд-во «Наука», 1975. – 256 с.
4. Bellman, R., Gross, O. Some combinatorial problems arising in the theory of multistage processes // Journ. Soc. industr. and appl. mathematics. – Vol. 2. – No. 3. – 1945.
5. Johnson, S.M. Optimal two- and three-stage production schedules with setup times included // Nav. res. log. quart. – Vol. 1. – No. 1. – 1954.
6. Конвей, Р.В. Теория расписаний / Р.В. Конвей, В.Л. Максвелл, Л.В. Миллер. – М.: Наука, 1975.
7. Батищев Д.И., Прилуцкий М.Х., Гудман Э.Д., Норенков И.П. Метод комбинирования эвристик для решения комбинаторных задач упорядочения и распределения ресурсов // Информационные технологии, – 1997. – ╧ 2. – С.29-32.
8. Норенков И.П. Комбинированные и генетические алгоритмы составления расписаний в задачах проектирования // Вестник МГТУ им. Н.Э. Баумана. – 1995. – ╧ 2. – С. 36-43.
9. Мышенков К.С., Романов А.Ю. Постановка задачи составления календарного плана ремонтов оборудования предприятия // Системный анализ в проектировании и управлении: Cб. науч. тр. XIV Междунар. науч.-практ. конф. / СПбГПУ. – СПб.: Изд-во Политехн. ун-та, 2010. – Ч. 1. – С. 240-243.
10. Hartmann S.A. Competitive Genetic Algorithm for Resource-Constrained Project Scheduling, Naval Research Logistics. – Vol. 45. – 1998. – pp. 733-750.
11. Hartmann S.A Self-Adapting Genetic Algorithm for Project Scheduling under Resource Constraints, Naval Research Logistics – Vol. 49. – 2002. – pp. 433-448.
12. Holland H.J. Adaptation in Natural and Artificial Systems. University of Michigan Press, Ann Arbor, 1975.
Публикации с ключевыми словами: генетический алгоритм, система управления ремонтами оборудования, промышленное предприятие, календарное планирование с ограниченными ресурсами, математическая постановка задачи
Публикации со словами: генетический алгоритм, система управления ремонтами оборудования, промышленное предприятие, календарное планирование с ограниченными ресурсами, математическая постановка задачи
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



