научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
УДК 652. 72
НИИ современных технологий, системного анализа и моделирования,
Иркутский государственный университет путей сообщения, г. Иркутск
Динамика механических систем, в которых отдельные элементы соединяются с другими через кинематические пары, традиционно рассматривается в теории механизмов и машин применительно к механизмам. Последние представляют собой механические цепи, состоящие из твердых тел, соединенных между собой кинематическими парами; механическая цепь является замкнутой и имеет, как правило, одно неподвижное звено [1, 2]. Однако сочленение может и не быть кинематической парой в общепринятом смысле, а представлять собой соединение более общего вида, в котором особенностями параметров движения обладают сопрягаемые точки двух звеньев; в частности, относительная скорость двух таких точек может быть постоянной или равна нулю (или равно нулю относительное смещение). Неудобства известных подходов к составлению математических моделей заключаются в необходимости учета переносных сил инерции, передаваемых от одного массоинерционного элемента к другому через сочленение, в том числе и через соединение в виде кинематических пар. Особенности динамических свойств таких механических систем представлены в работе [3]. Автором данной статьи рассматриваются некоторые приемы по построению математических моделей механических колебательных систем с сочленениями. Эти приемы позволяют упростить учет переносных сил инерции, возникающих, например, при кинематическом возмущении в системе, один из массоинерционных элементов которой имеет сочленение с вибрирующим основанием. Предлагаемый прием можно соотнести с приемами наложения связей в колебательных системах [4, 5].
Основная идея построения математических моделей заключается в том, чтобы получение математической модели проходило в специально выбранной системе обобщенных координат. Такая система должна содержать координаты относительного движения, которое в случае формирования сочленения «исключается», а соответствующая координата относительного движения принимается, равной нулю. В формализованном виде математическая модель системы с сочленениями может быть получена из матрицы коэффициентов дифференциальных уравнений исходной системы путем исключения соответствующих строки и столбца, для которых соответствующая координата принимается равной нулю; исключается при этом и соответствующая обобщенная сила. Перегруппировка обобщенных сил на соответствие обобщенным координатам происходит непосредственно в процессе вывода уравнений, и как отдельная операция, может не применяться. Истоки подхода, как уже упоминалось, связаны с понятиями наложения связей, которые нашли отражение в ряде работах, в частности в [5, 6].
I. Общие положения. Сочленения, которые реализуются через соединения между собой различных звеньев (в частности, звеньев, в виде твердых тел, в том числе и неподвижное звено), можно рассматривать как наложение связей. Так, например, связь ![]() , (где в свою очередь,
, (где в свою очередь, ![]() , а
, а ![]() ), можно записать как линейное однородное уравнение относительно координат системы. Если
), можно записать как линейное однородное уравнение относительно координат системы. Если ![]() и задача заключается в выполнение этого условия при движении системы, то уравнение может принять вид
и задача заключается в выполнение этого условия при движении системы, то уравнение может принять вид
![]() . (1)
. (1)
Такая задача может рассматриваться при движении цепной механической цепи при увеличении жесткости k2 до ∞ между элементами с массами m1 и m2 (рис. 1).

Рис. 1. Расчетная схема виброзащитной системы цепного типа с возможностями сочленения звеньев с массами m1 и m2
В общем случае можно полагать, что связь задана уравнением
![]() , (2)
, (2)
где q1, q2…qn – обобщенные координаты системы.
Предполагается, что налагаемая связь не должна приводить к смещению положения равновесия, в котором по предложению все qi=0, то есть
![]() , (3)
, (3)
что характерно для многих случаев виброзащитной практики.
Если разложить (3) по степеням координат yi, начиная с членов первого порядка, и ограничиться только такими членами разложения, то уравнение связи можно представить в виде
![]() , (4)
, (4)
где A11, A12…A1n – постоянные числа – коэффициенты, отражающие свойства механической системы.
II. Учет наложения связей. Введем новую систему координат, используем (4) и получим
 (5)
(5)
От такой подстановки собственные частоты не изменятся (по существу одна система обобщенных координат заменяется на другую). Кинетическая и потенциальная энергии в новых координатах ![]() , примут вид
, примут вид
 . (6)
. (6)
Отметим, что две квадратичные формы, из которых одна определенно положительна, одним линейным преобразованием могут быть приведены к каноническому виду [5].
Малые колебания системы с n степенями свободы около положения устойчивого равновесия, определяемые изменениями обобщенных координат, имеют вид:
 (7)
(7)
и представляют собой линейные наложения n главных гармонических колебаний [5].
Введем выражение, которое отражает ряд подстановок, например, (5), в результате которых частотное уравнение системы принимает вид
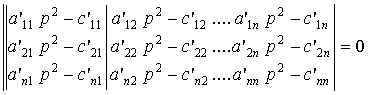 . (8)
. (8)
Предположим теперь, что на систему накладывается связь (4), то есть формируется сочленение через процедуру устремления к нулю некоторой выбранной координаты относительного движения. В новых координатах ri такая связь имеет уравнение
![]() . (9)
. (9)
При этом, n-1 корней ![]() системы с сочленением располагаются между корнями pk частотного уравнения исходной системы, что следует из теоремы о наложении связей [5]:
системы с сочленением располагаются между корнями pk частотного уравнения исходной системы, что следует из теоремы о наложении связей [5]:
![]() . (10)
. (10)
Таким образом, если на систему с n степенями свободы наложена линейная связь, то частоты полученной системы с n-1 степенями свободы располагаются между частотами первоначальной системы. То есть наложение связи, в соответствии с теорией колебаний, не нарушает условий движения, в смысле их осуществимости и устойчивости, но приводит к сдвигам в спектре частот собственных колебаний [5]. Такой подход может быть также расширен на случай нескольких сочленений (или связей). Если на систему с n степенями свободы наложены ![]() линейных связей
линейных связей
![]() , (11)
, (11)
![]()
то частота системы с сочленениями
![]() ,
,
удовлетворяют неравенствам такого же типа, что и (10).
Связи (11) можно всегда представить уравнениями
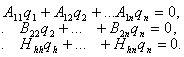 (12)
(12)
и налагать их на заданную систему не сразу все, а последовательно – одна за другой. Переход к координатам, связанным с qi соотношением (5), не изменяет уравнений естественных связей [5]. Положив r1 = 0, получим систему с n-1 степенями свободы, собственные частоты ![]() , которые удовлетворяют неравенству
, которые удовлетворяют неравенству
![]() , (13)
, (13)
что можно преобразовать относительно координат ![]() , связанных с
, связанных с ![]()
![]() уравнениями
уравнениями
 (14)
(14)
Полагая S2 = 0, получим систему с n-2 степенями свободы, частоты которой ![]() будут удовлетворять неравенствам
будут удовлетворять неравенствам
![]() . (15)
. (15)
Продолжая процедуры и вводя последовательно сочленения (связи), можно получить соответствующие неравенства, которые будут иметь место для частот системы после наложения на нее всех ![]() связей. Отметим, что предлагаемые приемы составления математических моделей позволяют детализировать представления о технологии формирования различных классов математических моделей и возможностях операции восстановления исходных моделей при «разборке» сочленения. Важным для нас обстоятельством является то, что формирование сочленения, в рамках теоретической механики, может рассматриваться как наложение связей. Этот процесс приводит к уменьшению числа степеней свободы исходной системы, которая существенным образом изменяет свои свойства. Поэтому формализм, связанный с уменьшением числа степеней свободы по отношению к механической системе, в которой исследуются последствия от введения сочленений, должен учитывать эти обстоятельства.
связей. Отметим, что предлагаемые приемы составления математических моделей позволяют детализировать представления о технологии формирования различных классов математических моделей и возможностях операции восстановления исходных моделей при «разборке» сочленения. Важным для нас обстоятельством является то, что формирование сочленения, в рамках теоретической механики, может рассматриваться как наложение связей. Этот процесс приводит к уменьшению числа степеней свободы исходной системы, которая существенным образом изменяет свои свойства. Поэтому формализм, связанный с уменьшением числа степеней свободы по отношению к механической системе, в которой исследуются последствия от введения сочленений, должен учитывать эти обстоятельства.
III. Заключение. Разные формы сочленений предполагают наличие особенностей в приемах соединений с учетом сложности их конструктивного исполнения. Чаще всего движение элементов системы происходит в одной плоскости; обычно выделяют два класса звеньев: неподвижные и подвижные. В связи с этим, одним из наиболее распространенных сочленений является шарнирное соединение в виде кинематической вращательной пары. В простейших вариантах звенья, соединяемые шарниром, допускают вращательно-качательные движения относительно друг друга. При этом сочленение из общего числа степеней свободы производит «исключение» одной степени свободы в движениях. Увеличение количества сочленений, соответствующих числу шарниров, обеспечивает уменьшение общего числа степеней свободы (или числа независимых переменных).
Кроме соединения подвижных звеньев между собой часто встречаются соединения твердых тел с неподвижными звеньями или с основанием (или условно неподвижной системой). Такое сочленение на рис. 2 показано подштриховкой.
|
Рис. 2. Расчетная схема ВЗС, имеющей сочленения: между подвижными звеньями, а также между подвижными и неподвижными звеньями (в точках А и В – сочленения в виде вращательных кинематических пар) |
Механические колебательные системы могут иметь сочленения различных типов, что обеспечивает особенности структуры системы и, так называемой, «метрики». Математическая модель системы может быть представлена в виде системы обыкновенных неоднородных дифференциальных уравнений второго порядка
![]() ,
,
где A– матрица операторных коэффициентов; y – вектор-столбец координат; b – вектор столбец внешних воздействий.
В общем случае матрица ![]() имеет порядок
имеет порядок ![]() и является симметричной:
и является симметричной:
 .
.
При построении математических моделей систем с сочленениями могут использоваться различные системы обобщенных координат, главным образом такие, в которых координаты отражают относительное движение. Сочленение может быть реализовано по отношению к элементу, совершающему «абсолютное» движение, то есть в неподвижной системе координат. Естественно, при этом, что системы координат допускают взаимные преобразования.
Введение сочленения означает исключение соответствующих столбцов и строк матрицы коэффициентов, включая и «исключения» соответствующей правой части уравнения [4].
Физический смысл операции заключается в том, что сочленение, представленное разностью соответствующих координат, исключается в физическом смысле; вместе с переменной исключаются одновременно и коэффициенты матрицы, определяющие связи между убираемой парциальной системой и остальными. Правая часть уравнения, определяемого строкой, также исключается, поскольку физически «исчезает» точка приложения сил. Внешнее воздействие в этом случае перераспределяется соответствующим образом при выборе систем обобщенных координат, где необходимо соблюдать условия равенства виртуальных работ обобщенных сил в различных системах обобщенных координат. В работах [7,8] рассматривается ряд конкретных примеров использования процедур, построения математических моделей, а также примеры сочленений. Набор возможных сочленений может обеспечивать и более сложные формы взаимодействий, в том числе и на основе кинематических пар IV и III, классов. Как полагает автор, возможности учета особенностей сочленения, в плане построения математических моделей, могут быть распространены и на другие системы с голономными связями.
Библиографический список
1. Артоболевский И.И. Теория механизмов и машин / И.И. Артоболевский. – М.: Наука, 1975. – 638 с.
2. Левитский Н.И. Колебания в механизмах / Н.И. Левитский – М.: Наука, 1988. – 356 с.
3. Лилов Л. К. Моделирование систем связанных тел: монография / Л.К.Лилов. - М. : Наука, 1993. - 272 с.
4. Хоменко А.П., Елисеев С.В. Виброзащитные системы с сочленениями. Технология построения математических моделей // Современные технологии. Системный анализ. Моделирование. Вып. 3 (27). – Иркутск. 2010. С. 8-18.
5. Бабаков И.М. Теория колебаний / И.М. Бабаков. – М.: Наука, 1968. – 549 с.
6. Лойцянский Л.Г. Курс теоретической механики: в 2 т. Т 2 Динамика / Л.Г. Лойцянский, А.И. Лурье. – М.: Наука, 1980. – 640 с.
7. Елисеев С.В. Возможности сочленения твердых тел в цепных механических системах / С.В. Елисеев, Ю.В. Ермошенко, И.В.Фомина // Современные технологии. Системный анализ. Моделирование – Иркутск: ИрГУПС, ╧3 (27). – 2010. – С. 138 – 146.
8. Хоменко А.П. Сочленения в виброзащитных системах как процесс уменьшения числа степеней свободы системы / // А.П. Хоменко, С.В. Елисеев // Современные технологии. Системный анализ. Моделирование. – Иркутск: ИрГУПС, ╧4(28). – 2010. – С.8 – 15.
Публикации с ключевыми словами: математические модели, колебательные системы с сочленениями, наложение связей
Публикации со словами: математические модели, колебательные системы с сочленениями, наложение связей
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




