научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2011
МГТУ им. Н.Э. Баумана
Задача декодирования кодов Рида-Соломона может быть решена различными способами. В [1] приведен обзор различных алгоритмов декодирования и сравнение эффективности их реализации. Наиболее ресурсоемкой частью декодера является схема решения ключевого уравнения. В [2, 3] приведено сравнение наиболее широко распространенных алгоритмов решения ключевого уравнения Берлекэмпа-Месси и Евклида с точки зрения аппаратной эффективности и быстродействия. В данной работе рассматривается реализация декодера на основе алгоритмов Берлекэмпа-Месси, Ченя и Форни [1, 2].
Рассмотрим процедуру определения позиций ошибок и вычисления их значений. Пусть в приемник поступило сообщение
r(x) = c(x) + e(x),
где c(x) – переданное сообщение, в которой в процессе передачи по каналу связи произошло ![]() ошибок, отображаемых многочленом e(x).
ошибок, отображаемых многочленом e(x).
Каждый ненулевой компонент e(x) описывается парой элементов: Yi – величина ошибки и Xi – локатор ошибки в позиции i. Yi, Xi – элементы GF(n), и элемент Xi = αi, αi ![]() GF(n).
GF(n).
Для описания ошибок используются:
1. Многочлен локаторов ошибок Λ(x):
![]()
имеющий корни xi =Xi–1, i = 1, …, ![]() , обратные к локаторам ошибок, то есть Xi–1· Xi = 1.
, обратные к локаторам ошибок, то есть Xi–1· Xi = 1.
2. Многочлен значений ошибок Ω(x):
Ω(x) = S(x)Λ(x) mod x2t,
где
![]()
синдромный многочлен бесконечной степени, для которого известны только 2t коэффициентов для поступившей комбинации кода Рида-Соломона.
Здесь
![]()
элемент синдрома, α j– корень порождающего многочлена РС-кода.
Значение Sj = e(α j) вычисляется как:
Sj = r(α j) = c(α j) + e(α j) = e(α j),
где m0 ≤ j ≤ m0 + 2t – 1 при m0 = 1.
Уравнение для многочлена значений ошибок определяет множество из (2t–υ) уравнений и называется ключевым уравнением, так как оно представляется “ключом” решения задачи декодирования. Это становится понятным, если учесть, что степень Ω(x) не превышает ![]() и поэтому справедливо:
и поэтому справедливо:
![]()
где
![]()
Из этого уравнения необходимо получить ![]() уравнений для
уравнений для ![]() неизвестных коэффициентов Λk. Эти уравнения являются линейными. После нахождения многочлена Λ(x) ключевое уравнение позволяет найти неизвестные компоненты вектора e(x) и по ним выходной вектор декодера
неизвестных коэффициентов Λk. Эти уравнения являются линейными. После нахождения многочлена Λ(x) ключевое уравнение позволяет найти неизвестные компоненты вектора e(x) и по ним выходной вектор декодера
c(x)= r(x) + e(x).
Решение ключевого уравнения является основной задачей декодирования кода Рида-Соломона. Прямолинейная реализация решения влечет за собой решение системы из 2t линейных уравнений. Для сокращения вычислительной сложности используются различные алгоритмы. Реализация декодеров на жесткой логике и ПЛИС рассмотрена в большом количестве работ, например, в [3, 4, 5]. Наиболее распространены алгоритмы, основанные на подходе Берлекэмпа-Месси [3] и алгоритмы, использующие алгоритм Евклида [4]. Алгоритмы с мягким решением, например алгоритм Судана, в аппаратных реализациях используются редко ввиду нерегулярности получаемой архитектуры.
Решение ключевого уравнения в алгоритме Берлекэмпа-Месси сводится к задаче итеративного построения минимального сдвигового регистра с линейной обратной связью, порождающего на выходе последовательность синдромов, соответствующую коэффициентам S(x) (см. рис. 1).
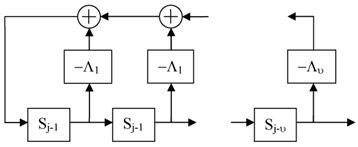
Рисунок 1. Сдвиговый регистр, определяющий многочлен локаторов
В алгоритме Берлекэмпа-Месси используется операция нахождения обратного в используемом поле, что значительно повышает сложность и снижает быстродействие аппаратуры, реализующей алгоритм. Имеются модификации алгоритма, не использующие делений (iBM). В работе [3] реализуется несколько архитектур на основе iBM и проводится их сравнение с реализациями алгоритма Евклида (см. таблицу 1). В таблицу также включена предлагаемая в данной работе архитектура CSiBM. Также в таблице 1 приведена оценка критического пути в комбинационной логике в виде задержки на используемых функциональных блоках.
Т А Б Л И Ц А 1
Архитектура | add | mult | reg | mux | Тактов | крит. путь | |
iBM (Блэйхут) | 2t+1 | 3t+3 | 4t+2 | t+1 | 3t | >2(Tmult+Tadd) | |
iBM (Берлекэмп) | 3t+1 | 5t+3 | 6t+2 | 2t+1 | 2t | >2(Tmult+Tadd) | |
riBM | 3t+1 | 6t+2 | 6t+2 | 3t+1 | 2t | Tmult+Tadd | |
RiBM | 3t+1 | 6t+2 | 6t+2 | 3t+1 | 2t | Tmult+Tadd | |
Евклид | 4t+2 | 8t+8 | 4t+4 | 8t+8 | 2t | Tmult+Tadd+Tmux | |
Евклид итерат. | 2t+1 | 2t+1 | 10t+5 | 14t+7 | 12t | Tmult+Tadd+Tmux | |
CSiBM | 2t+1 | 2t+2 | 5t+3 | 5t+1 | 6t | Tmult+Tadd+2Tmux | |
Здесь
add – число сумматоров в GF(28);
mult – число умножителей в GF(28);
reg – число регистров разрядности 8;
mux – число мультиплексоров 2 в 1 разрядности 8;
В базисе ПЛИС высокой и сверхвысокой степени интеграции комбинационная логика реализуется в базисе таблиц перекодировки. Приведем объем требуемых ресурсов для операций над 8-ми разрядными символами для четырехвходовых таблиц перекодировки (ТП), которые используются в ряде семейств Stratix и Cyclone фирмы Altera, Virtex и Spartan фирмы Xilinx:
· add – 8 ТП (возможно сложение от 2 до 4 символов)
· mult – 50 ТП
· mux – 8 ТП
В таблице 1 для ряда архитектур дана неточная оценка задержки критического пути, связанная с различной эффективностью реализации дерева сумматоров в разных аппаратных архитектурах и дополнительной задержки в схеме управления.
Задержку критического пути в комбинационной схеме можно оценить по его длине - максимальному количеству ТП, через которые проходит сигнал.
· add – 1 ТП
· mult – 4 ТП
· mux – 1 ТП
В таблице 2 приведена оценка количества используемых ТП, регистров и длина критического пути в ТП.
Т А Б Л И Ц А 2
Архитектура | ТП | reg | тактов | крит. путь, ТП |
iBM (Блэйхут) | 166t+166 | 32t+16 | 3t | >10 |
iBM (Берлекэмп) | 292t+166 | 48t+16 | 2t | >10 |
riBM | 348t+116 | 48t+16 | 2t | 5 |
RiBM | 348t+116 | 48t+16 | 2t | 5 |
Евклид | 496t+480 | 32t+32 | 2t | 6 |
Евклид итерат. | 220t+114 | 80t+40 | 12t | 6 |
CSiBM | 156t+116 | 40t+24 | 6t | 7 |
Логический элемент ПЛИС с четырехвходовой ТП содержит одну ТП и один регистр, которые могут использоваться одновременно. Таким образом, общее количество требуемых для реализации логических элементов можно примерно оценить как максимальное значение от количества регистров и ТП. Исходя из этого, для всех рассматриваемых архитектур решателей ключевого уравнения оценка ресурсоемкости может проводиться по количеству используемых ТП.
При синтезе комбинационных схем функции минимизируются синтезатором совместно, что может приводить к сокращению конечного объема проекта и количества слоев логики. Это существенно зависит от применяемого синтезатора и архитектуры ПЛИС, однако соотношения для различных архитектур решателей, как правило, остаются неизменными.
В ряде задач, например, в системах цифрового телевидения [6,7] требуется обрабатывать пакеты укороченного кода длиной от 69 символов с t=8. При реализации потоковой обработки в темпе поступления информации с аппаратной точки зрения это накладывает ограничение по числу тактов работы алгоритма не более 69. Это сразу исключает из рассмотрения компактную итеративную реализацию алгоритма Евклида, требующую 96 тактов для t=8. Обычная (параллельная) реализация алгоритма Евклида требует намного большего, чем вариации алгоритма Берлекэмпа-Месси, количества умножителей, что значительно повышает объем проекта, так как умножитель является наиболее ресурсоемким функциональным блоком, используемым при декодировании. В дополнение к известным алгоритмам iBM в трактовке Блэйхута и Берлекэмпа, авторами работы [3] также предложены аппаратно избыточные алгоритмы riBM и RiBM, позволяющие достичь более высокой тактовой частоты. Однако, в пространстве решений нет промежуточного по быстродействию и объему решения между итерационным алгоритмом Евклида и различными реализациями алгоритма Берлекэмпа-Месси.
Для создания промежуточного решения CSiBM (cycle-shared iBM – iBM с разделением по тактам) используем в качестве основы алгоритм iBM в реализации [5]. Алгоритм iBM требует наименьшее количество умножителей и выдает результат (коэффициенты многочлена локаторов ошибок и многочлена значений ошибок) за 3t тактов. Для повышения тактовой частоты и уменьшения объема используемых ресурсов была реализована дополнительная конвейеризация с разделением использования умножителей между тактами. По этой причине алгоритм CSiBM требует 6t тактов.
Рассмотрим алгоритм Берлекэмпа-Месси без инверсий более подробно. Алгоритм требует 3t шагов. На первых 2t шагах осуществляется определение коэффициентов полинома β*Λ(x), на следующих t шагах определяются коэффициенты полинома β*Ω(x), где β – некоторая скалярная величина. Так как умножение на β не влияет на корни полинома Λ(x), а отношение Λ(x) и Ω(x) не изменяется при умножении их на β, это не изменяет определяемые в дальнейшем алгоритмами Ченя и Форни положение и величины ошибок. Ниже приведен псевдокод алгоритма.
Входы:
Si, i=0,1,2,…,2t-1;
Переменные:
B(x) – полином корректора;
Δ – невязка;
Γ – масштабирующий коэффициент, вводится для устранения деления;
K – текущая длина регистра сдвига.
Инициализация.
Λ0(0)=B0(0)=1, Λi(0)=Bi(0)=0 для i=1,2,…,t; K(0)=0; Γ(0)=1;
Итерации:
от r=0 до 2t-1 с шагом 1
{
Шаг 1. Вычисление невязки:
Δ(r)=Sr* Λ0(r)+ Sr-1* Λ1(r)+…+ Sr-t* Λt(r)
Шаг 2. Коррекция полинома локаторов:
Λi(r+1)= Γ(r)* Λi(r)- Δ(r)*Bi-1(r), i=0,1,…,t
Шаг 3. Обновление корректора и длины:
если ((Δ(r)!=0) и (K(r)*2<=r))
{
Bi(r+1)= Λi(r), i=0,1,…,t
Γ(r+1)= Δ(r)
K(r+1)=r-K(r)
}
иначе
{
Bi(r+1)= Bi-1(r), i=0,1,…,t
Γ(r+1)= Γ(r)
K(r+1)=K(r)
}
}
Шаг 4. Расчет полинома ошибок:
от i=2t до 3t-1 с шагом 1
Ωi(2t)=Si* Λ0(2t)+ Si-1* Λ1(2t)+…+ S0* Λi(2t)
Выходы:
Λi(2t), i=0,1,…,t
Ωi(2t), i=0,1,…, t-1
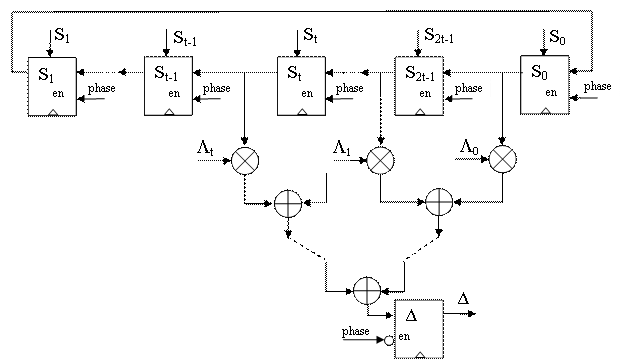
Аппаратная реализация данного алгоритма в предлагаемой архитектуре CSiBM использует два типа функциональных блоков. Шаг 1 реализуется модулем расчета невязки (рис. 2). Перед началом работы алгоритма осуществляется загрузка сдвигового регистра значениями синдромов Si. Следует заметить, что на первых t циклах работы алгоритма согласно описанию шага 1 должны использоваться значения S-1, S-2 и т.д., а не загруженные значения. Однако, так как начальные значения коэффициентов локаторов Λ, на которые они умножаются, равны нулю, это не влияет на работу алгоритма. Загруженные значения синдромов S, будут использоваться на следующих циклах при их перемещении по сдвиговому регистру. Вычисленное значение невязки сохраняется в регистре невязки.
В данном модуле критический путь от регистра, содержащего S, до регистра невязки состоит из умножителя и дерева сумматоров 8 в 1. Однако, так как одна таблица перекодировки реализует сложение до 4 операндов, данное дерево реализуется схемой с длиной критического пути Tmult+2Tadd, что меньше задержки Tmult+Tadd+3Tmux, приведенной в табл. 1, которая ограничивает тактовую частоту в рассматриваемом ниже модуле коррекции.
|
|
Рисунок 2. Модуль расчета невязки |
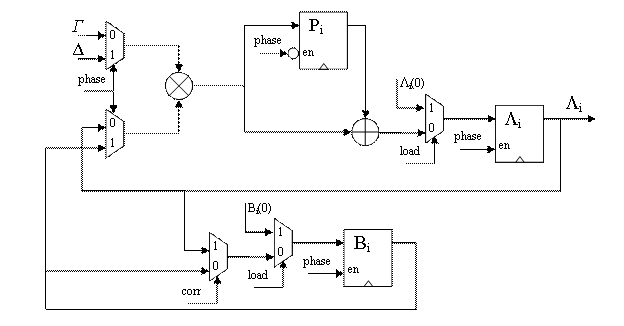
Шаг 2 реализуется модулями коррекции, идентичными для всех коэффициентов Λi. (рис. 3).
|
Рисунок 3. Модуль коррекции |
Одна итерация циклов алгоритма выполняется за два такта. Выполнение шага 1 и умножения Γ(r)* Λi(r) на шаге 2 осуществляется на первом такте в модуле коррекции (phase=0), результат вычисления невязки сохраняется в регистре невязки (рис. 2). Выполнение второго умножения Δ(r)*Bi-1(r) на шаге 2 и шага 3 осуществляется на втором такте (phase=1). Это разбивает критический путь в схеме и позволяет реализовать умножения, выполняемые на шаге 2 на одном умножителе. Критический путь в данной схеме проходит от выхода до входа регистра Λi через два мультиплексора, умножитель и сумматор.
Результатом работы первого цикла, состоящего из шагов 1, 2 и 3 являются коэффициенты многочлена локаторов ошибок Λi. На шаге 4 реализуется расчет коэффициентов многочлена ошибок Ωi, при этом вычисленные коэффициенты Λi фиксируются и модуль расчета невязки используется для расчета Ωi. Вычисленные значения Ωi сохраняются в регистрах, использовавшихся для хранения Bi. Для этого и для начальной загрузки коэффициентов используется сигнал load.
Заключение
Разработан модифицированный вариант архитектуры решателя ключевых уравнений для декодера Рида-Соломона на основе алгоритма Берлекэмпа-Месси без инверсии. По сравнению с существующими реализациями, оптимизированными по объему или по быстродействию, предложенная схема предоставляет новый вариант баланса между объемом и быстродействием. Объем требуемых ресурсов меньше всех рассмотренных реализаций алгоритма iBM, но при этом достижимая частота работы схемы примерно в два раза выше по сравнению с базовым алгоритмом iBM. Время решения в тактах составляет 6t против 3t для алгоритма iBM, однако для большинства используемых кодов это меньше длины кода, что позволяет декодировать информацию в темпе поступления данных.
Литература
1. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.:Техносфера, 2005 – 320c.
2. Р.Блэйхут. Теория и практика кодов, контролирующих ошибки. Пер. с англ. – М.: Мир, 1986. – 576 c., ил.
3. D.V.Sarwate, N.R.Shanbhag. High-Speed Architectures for Reed-Solomon Decoders. IEEE Transcations on VLSI Systems, Vol. 9, No. 5, October 2001, pp. 641-655.
4. H. Lee. High-Speed VLSI Architecture for Parallel Reed-Solomon Decoder. IEEE Transactions on VLSI Systems, Vol. 11, No. 2, April 2003, pp. 288-294.
5. I. S. Reed, M. T. Shih, T. K. Truong, “VLSI design of inverse-free Berlekamp–Massey algorithm,” Proc. Inst. Elect. Eng., pt. E, vol. 138, pp. 295–298, Sept. 1991.
6. ETSI EN 300 421 Digital Video Broadcasting (DVB); Framing structure, channel coding and modulation for 11/12 GHz satellite services.
7. ETSI EN 301 790. Digital Video Broadcasting (DVB); Interaction channel for satellite distribution systems.
Публикации с ключевыми словами: коды Рида-Соломона, алгоритм Берлекемпа-Месси, ПЛИС
Публикации со словами: коды Рида-Соломона, алгоритм Берлекемпа-Месси, ПЛИС
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||